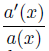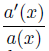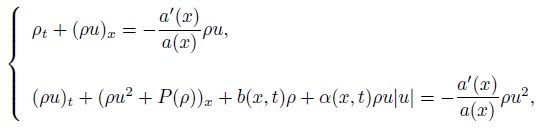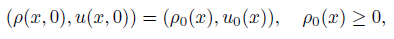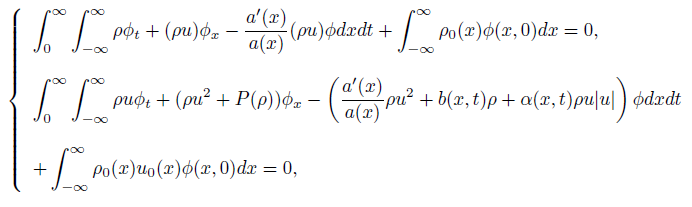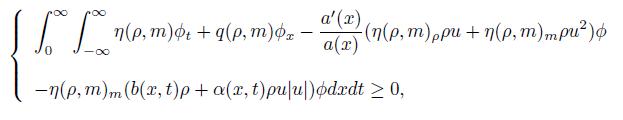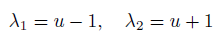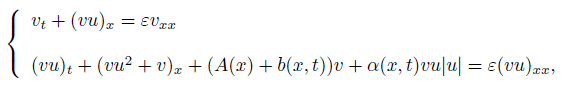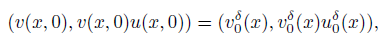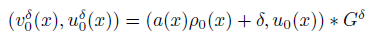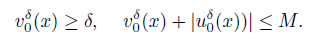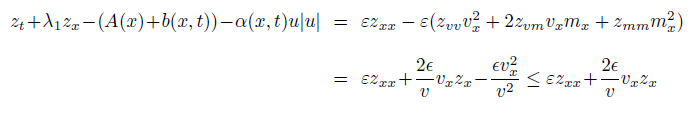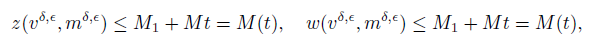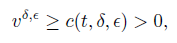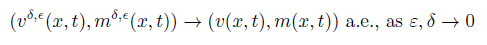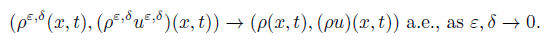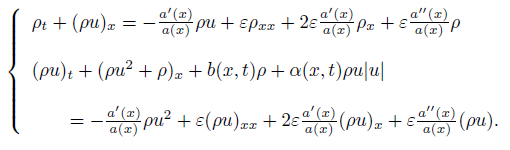Artículos Originales
Global Solutions to Isothermal System with Source
Soluciones globales para sistema isotérmico con fuente
1Wuxi Institute of Technology
Abstract
In this short note, we are concerned with the global existence of solutions to the isothermal system with source, where the inhomogeneous terms f(x, t, ρ, u) = b(x, t)ρ + ρu2 + α(x, t)ρu|u| are appeared in the momentum equation. Our work extended the results in the previous papers “Resonance for the Isothermal System of Isentropic Gas Dynamics” (Proc. A.M.S.139(2011),2821-2826), “Global Existence and Stability to the Polytropic Gas Dynamics with an Outer Force” (Appl. Math. Letters, 95(2019), 35-40) and “Existence of Global Solutions for Isentropic Gas Flow with Friction” (Nonlinearity, 33(2020), 3940-3969), where the global solution was obtained for the source f(x, t, ρ, u) =
ρu2 + α(x, t)ρu|u| are appeared in the momentum equation. Our work extended the results in the previous papers “Resonance for the Isothermal System of Isentropic Gas Dynamics” (Proc. A.M.S.139(2011),2821-2826), “Global Existence and Stability to the Polytropic Gas Dynamics with an Outer Force” (Appl. Math. Letters, 95(2019), 35-40) and “Existence of Global Solutions for Isentropic Gas Flow with Friction” (Nonlinearity, 33(2020), 3940-3969), where the global solution was obtained for the source f(x, t, ρ, u) = ρu2 , f(x, t, ρ, u) = b(x, t)ρ, f(x, t, ρ, u) = α(x, t)ρu|u| respectively.
ρu2 , f(x, t, ρ, u) = b(x, t)ρ, f(x, t, ρ, u) = α(x, t)ρu|u| respectively.
Keywords Global L∞ solution; isothermal system; source terms; compensated compactness; MSC2010: 35L45; 35L60; 46T99
Resumen
En esta nota estamos interesados en la existencia global de soluciones para el sistema isotérmico con fuente, donde los términos no homogéneos f(x, t, ρ, u) = b(x, t)ρ + 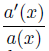 ρu2 + α(x, t)ρu|u| aparecen en la ecuación de momento. Nuestros resultados extienden los presentados en “Resonance for the Isothermal System of Isentropic Gas Dynamics” (Proc. A.M.S.139(2011),2821-2826), “Global Existence and Stability to the Polytropic Gas Dynamics with an Outer Force” (Appl. Math. Letters, 95(2019), 35-40) y “Existence of Global Solutions for Isentropic Gas Flow with Friction” (Nonlinearity, 33(2020), 3940-3969), en los cuales la solución global se obtuvo, respectivamente, para las fuentes f(x, t, ρ, u) =
ρu2 + α(x, t)ρu|u| aparecen en la ecuación de momento. Nuestros resultados extienden los presentados en “Resonance for the Isothermal System of Isentropic Gas Dynamics” (Proc. A.M.S.139(2011),2821-2826), “Global Existence and Stability to the Polytropic Gas Dynamics with an Outer Force” (Appl. Math. Letters, 95(2019), 35-40) y “Existence of Global Solutions for Isentropic Gas Flow with Friction” (Nonlinearity, 33(2020), 3940-3969), en los cuales la solución global se obtuvo, respectivamente, para las fuentes f(x, t, ρ, u) = 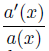 ρu2 , f(x, t, ρ, u) = b(x, t)ρ and f(x, t, ρ, u) = α(x, t)ρu|u|.
ρu2 , f(x, t, ρ, u) = b(x, t)ρ and f(x, t, ρ, u) = α(x, t)ρu|u|.
Palabras clave Soluciones L∞ globales; sistemas isotérmicos; términos fuente; compacidad compensada
1. Introduction
In this paper, we studied the global entropy solutions for the Cauchy problem of isentropic gas dynamics system with source
with bounded measurable initial data
where ρ is the density of gas, u the velocity, P = P(ρ) the pressure. The function b(x, t) corresponds physically to the slope of the topography, α(x, t)ρ|u| to a friction term, where α(x, t) denotes a coefficient function and a(x) is a slowly variable cross section area at x in the nozzle.
The pressure-density relation is P(ρ) = , where γ > 1 is the adiabatic exponent and for the isothermal gas, γ = 1.
, where γ > 1 is the adiabatic exponent and for the isothermal gas, γ = 1.
System (1) is of interest because it has different physical backgrounds. For the case of nozzle flow without the friction, namely b(x, t) = 0 and α(x, t) = 0, the global solution of the Cauchy problem was well studied (cf. [1, 2, 7, 9] and the references cited therein); When a(x) = 0 and α(x, t) = 0, the source term b(x, t) in System (1) is corresponding to an outer force [3, 8], and when b(x, t) = 0, a(x) = 0, α(x, t)u|u| in (1) corresponds physically to a friction term [5].
In this paper we study the isothermal case P(ρ) = ρ and prove the global existence of weak solutions for the Cauchy problem (1)-(2) for general bounded initial data. The main result is given in the following:
Theorem 1.1. Let P(ρ) = ρ, 0 < aL ≤ a(x) ≤ M for x in any compact set x ∈ (−L, L), A(x) = − 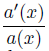 ∈ C1 (R), 0 ≤ α(x, t) ∈ C1 (R × R+) and |A(x)| + α(x, t) ≤ M, where M, aL are positive constants, but aL could depend on L. Then the Cauchy problem (1)-(2) has a bounded weak solution (ρ, u) which satisfies system (1) in the sense of distributions
∈ C1 (R), 0 ≤ α(x, t) ∈ C1 (R × R+) and |A(x)| + α(x, t) ≤ M, where M, aL are positive constants, but aL could depend on L. Then the Cauchy problem (1)-(2) has a bounded weak solution (ρ, u) which satisfies system (1) in the sense of distributions
for all test function ϕ ∈ C10 (R × R+), and
where (η, q) is a pair of entropy-entropy flux of system (1), η is convex, and ϕ ∈ 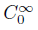 (R× R+ − {t = 0}) is apositive function.
(R× R+ − {t = 0}) is apositive function.
2. Proof of Theorem 1
In this section, we shall prove Theorem 1. Let v = ρa(x), then we may rewrite (1) as
By simple calculations, the two eigenvalues of (5) are
with corresponding Riemann invariants
To prove Theorem 1, we consider the Cauchy problem for the following parabolic system
with initial data
where δ > 0, ε > 0 denote a regular perturbation constant, the viscosity coefficient,
and Gδ is a mollifier.
Then
and
We multiply (8) by (wv, wm) and (zv, zm), respectively, to obtain
and
Letting z = 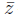 +M t, w =
+M t, w = 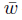 +M t, where M is the bound of |A(x)|+α(x, t), we have from (13)-(14) that
+M t, where M is the bound of |A(x)|+α(x, t), we have from (13)-(14) that
and
Since α(x, t) ≥ 0, using the maximum principle to (15)-(16) (See Theorem 8.5.1 in [6] for the details), we have the estimates on the solutions (v δ,ϵ, m δ,ϵ) of the Cauchy problem (8)-(9)
or
where M1 is a positive constant depending only on the bounds of the initial date. Therefore we have the following estimates from (17)
which deduce the following positive, lower bound of v δ,ϵ, by using the results in Theorem 1.0.2 in [6],
where c(t, δ, ϵ) could tend to zero as the time t tends to infinity or δ, ϵ tend to zero, and M1(t) is a suitable positive function of t, independent of ε, δ.
With the uniform estimates given in (18) and (19), we may apply the compactness framework in [4] to obtain the pointwise convergence of the viscosity solutions
We rewrite (8) as
Multiplying a suitable test function ϕ to system (22) and letting ϵ go to zero, we can prove that the limit (ρ(x, t), u(x, t)) in (21) satisfies system (1) in the sense of distributions and the Lax entropy condition (3) and (4). So, we complete the proof of Theorem 1.
References
[1] Cao W.-T., Huang F.-M. and Yuan D.-F., “Global Entropy Solutions to the Gas Flow in General Nozzle”, SIAM. Journal on Math. Anal, 51 (2019), No. 4, 3276-3297. doi: 10.1137/19M1249436
[ Links ]
[2] Chen G.-Q. and Glimm J., “Global solutions to the compressible Euler equations with geometric structure”, Commun. Math. Phys 180 (1996), 153-193. doi: 10.1007/BF02101185
[ Links ]
[3] Hu Y.-B, Lu Y.-G. and Tsuge N., “Global Existence and Stability to the Polytropic Gas Dynamics with an Outer Force”, Appl. Math. Lett, 95 (2019), 36-40. doi: 10.1016/j.aml.2019.03.022
[ Links ]
[4] Huang F.-M. and Wang Z., “Convergence of Viscosity Solutions for Isentropic Gas Dynamics”, SIAM J. Math. Anal, 34 (2003), 595-610.doi: 10.1137/S0036141002405819
[ Links ]
[5] Lu Y.-G., “Existence of Global Solutions for Isentropic Gas Flow with Friction”, Nonlinearity, 33 (2020), No 8, 3940-3969. doi:10.1088/1361-6544/ab7d20
[ Links ]
[6] Lu Y.-G., Hyperbolic Conservation Laws and the Compensated Compactness Method, Chapman and Hall, vol. 128, Boca Ratón, 2002.
[ Links ]
[7] Lu Y.-G., “Resonance for the isothermal system of isentropic gas dynamics”, Proc. A.M.S., 139 (2011), 2821-2826. doi: 10.1090/S0002-9939-2011-10733-0
[ Links ]
[8] Tsuge N., “Existence and Stability of Solutions to the Compressible Euler Equations with an Outer Force”, Nonlinear Analysis, Real World Applications, 27 (2016), 203-220. doi: 10.1016/j.nonrwa.2015.07.017
[ Links ]
[9] Tsuge N., “Isentropic Gas Flow for the Compressible Euler Equations in a Nozzle”, Arch. Rat. Mech. Anal, 209 (2013), No. 2, 365-400. doi: 10.1007/s00205-013-0637-5
[ Links ]
 , where γ > 1 is the adiabatic exponent and for the isothermal gas, γ = 1.
, where γ > 1 is the adiabatic exponent and for the isothermal gas, γ = 1.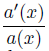 ∈ C1 (R), 0 ≤ α(x, t) ∈ C1 (R × R+) and |A(x)| + α(x, t) ≤ M, where M, aL are positive constants, but aL could depend on L. Then the Cauchy problem (1)-(2) has a bounded weak solution (ρ, u) which satisfies system (1) in the sense of distributions
∈ C1 (R), 0 ≤ α(x, t) ∈ C1 (R × R+) and |A(x)| + α(x, t) ≤ M, where M, aL are positive constants, but aL could depend on L. Then the Cauchy problem (1)-(2) has a bounded weak solution (ρ, u) which satisfies system (1) in the sense of distributions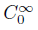 (R× R+ − {t = 0}) is apositive function.
(R× R+ − {t = 0}) is apositive function.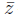 +M t, w =
+M t, w = 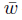 +M t, where M is the bound of |A(x)|+α(x, t), we have from (13)-(14) that
+M t, where M is the bound of |A(x)|+α(x, t), we have from (13)-(14) that