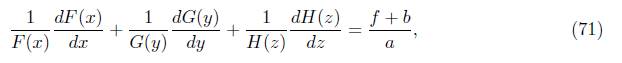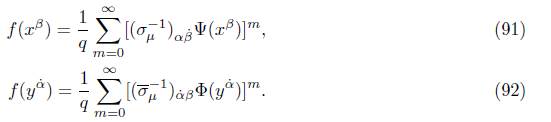1. Introduction

Based on the work of Beretetskii et al., Lachieze-Rey, Gori et al., and Cartan, the spinor ψ ^α is defined as a magnitude components α = 1, 2 expressed as

and its complex conjugate φ˙ in terms of the rotation matrices (see [²],[³],[⁵],[⁴] for more details). Based on the work of the aforementioned authors, there are two types of operations on spinors, which are reflections and rotations. In group theory, the set of rotations described by the matrices with complex entries is group SU(2), whose generators are the Pauli matrices, described in the work of Zettili [⁷]. In regards to rotation matrices, Gori et al. mentioned in their work that rotation matrices originated Pauli matrices in the form of:

being θ the angle of rotation [⁴]. Beretetskii et al. defined the covariance and contravariance over the spinors by the relation ψ ^′1 = ψ ₂ , ψ ^′2 = −ψ ₁ from the matrix

and, similarly, for pointed spinors, ψ _1˙ = ψ ² , ψ _2˙ −ψ ¹ [³]. The same author defined bispinors as the pair (ψ ^α , φ _α˙ ), which form a broader group of Lorentz, and, with them, the scalar product is formulated as (ψ ^α , φ _α˙ ) · (f ^α , h _α˙ ). The author of the reference [⁵] mentions algebra Cl(3) as a space-time formulation generated by vectors e _µ , which form a basis for ℝ ^1,3 that satisfies the relation e _µ · e _ν = g _µν , inducing a 16-membered basis, as described below:

In accordance with the previous statements, the same author described the Weyl spinors as

and the Dirac spinor

as defined in the work of Beretetskii et al [³].

The q-Lorentzian algebra was defined in the reference [¹]. The quantum complex spinors have components ψ1 and ψ2 and conjugates φ1 and φ˙ . They meet the following q-relations.

Definition 1.1. Considering spinors ψ ^α , φ ^α and {τ ¹ , T ² , S ¹ , σ ²} as the generators of the q-Lorentzian algebra for the group U _q (su(2)) [⁶], we have:

1. For ψ ^α , α = 1, 2

2. Their complex conjugates

Deformed commutation relations for q-Lorentzian algebra are defined in the next proposition, on the quantum-symmetric plane and the quantum anti-symmetric plane.

Proposition 1.2. Considering generator T of the set {τ ¹ , T ² , S ¹ , σ ²} for the algebra Uq(su(2)) and the relations 2, 3, and 4, defined in [¹] and [⁶] . The q-Lorentzian algebra for spinors in the deformed space is defined through the following relations:

Definition 1.3. The following matrices are the bosonic q-deformed Minkowskian Pauli spin matrices defined in the Schmidt work [⁶]:

Likewise, the conjugated Pauli matrices are:

The inverse Pauli matrices

Finally

The purpose of this article is to define the q-Lorentzian spinor variables and q-spinor differential and integral calculus and q-differential spinor equation. The paper is organized in: section 2 where it is presented the q-spinor variables and calculus. In section 3 we present the q-differential spinor equation, and the final section with comments.

2. q-Spinor variables and calculus

Definition 2.1. The q-Lorentzian spinor variables or q-spinor variables are defined according to the expressions (2), (3), and (4) as follows:

Definition 2.2. We consider the set 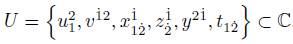A function on the q-spinor variables is defined as

Definition 2.3. Let f, g: U −→ ℂ be functions and u ^β ∈ U. The following properties are satisfy on the q-spinor variables, we state some clear properties of the functions on the q-spinor variables

Definition 2.4. For a function f: U −→ ℂ and u ^β ∈ ℂ, the q-spinor derivative is defined as:

and its conjugate complex

Proposition 2.5. Let V ⊂ ℂ be the set conformed by q-spinor variables in the form

The q-spinor functions in complex variable f: V → ℂ can be expressed as:

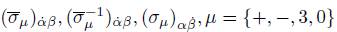the deformed spin matrices in the Minkowski space defined in the introduction.

Theorem 2.6. Assume that f: ℂ → C and g: ℂ → C are spinorial differentiable functions at u ^β , v ^α ˙ ∈ ℂ . Then

1. the sum g + h: ℂ → ℂ is q-differentiable at u ^β and

2. the product gh: ℂ → ℂ is q-differentiable at u ^β and

3. (u ^β ) ⁿ : ℂ → ℂ is q-differentiable at u ^β and

Proof. 1.

2.

3.

multiplying by

Remark 2.7. The proof for f(v ^α˙ ) is similar.

Example 2.8. 1. For f(u ^β ) = u ^β

With these results, it is possible to define that q-spinor complex integral formula by the following theorem.

Theorem 2.9. Let Γ _q be the closed contour of the deformed quantum complex plane, and u ^β ₀ , v ^α˙ ⊂ Γ _q point spinors contained in the contour. The q-spinor complex integral formulas are defined by:

Proof. d _q f is found form (38) and is integrated over closed contour Γ _q

the left side of (48) may be equalated to , obtaining

taking into account point spinors, then defined and, by substituting in (49), the following is obtained:

The expressions (44) and (45) are obtained by equalating terms that depend on f((qu ₀) ^β and f(u ^β ₀ ). The same process is applied to get (46) and (47) from (39).

Example 2.10. Considering the following spinorial function f(v ¹²) = (v ¹²)² , and the point spinor v ¹² ₀ = qv ¹² contained in the closed contour Γ _q . Applying (46) we have

taking in account the spinorial matrices defined in the Schmidtťs work [⁶] (check Introduction) and if µ = −, then

and for the case µ = + the integral is zero.

3. q-Differential spinor equation

Based on the Pauli matrices presented in the works of Gori and Zettili [⁴],[⁷], 4×4 rotation matrices were defined in the following proposition.

Proposition 3.1. The 4 × 4 rotation matrices can be expressed as follows:

With these rotation matrices, we can propose the following spinors, using as a starting point the definitions proposed by Beretetskii et al and Lachieze [³], [⁵].

Proposition 3.2. The spinors ψ _α ^β and φ ^α˙ _˙ can be expressed as follows:

and, when related to (50), spinorial components ψ _x , ψ _y , ψ _z , φ _x˙ , φ _y˙ and φ _z˙ are defined

and explicitly:

These expressions are conveyed as:

Remark 3.3. Beretetskii et al., define the bispinors as the pair (ψ ^α , φ _α˙ ), formulating product between bispinors [³]:

4. Comments

In section 3, a combination of the q-Lorentzian algebra formalism and the deformed complex vari-able is proposed based on section 2, though the latter is not explicit in the literature. Nevertheless, its development can be totally formulated from its derivatives mentioned in expressions (38) and (39), and its spinor contour integral q-forms, described by (44) - (47). These last expressions contain deformed spin matrices (σµ) αβ), (σ ⁻¹ _µ )αβ˙ defined in Schmidt work [⁶]. It should be empha-sized, that in this case, these matrices are formulated in the Minkowski space and that they are also spin-boson matrices. Hopefully, in future works, the spinor complex q-variable formulation can be achieved, but for the fermionic part. In section 3, a spinor partial differential equation (given by (58)) was proposed, and its solutions are given by theorem 4. Its solutions were obtained using angle θ = π/2. Clearly, (77) and (87) are not unique, which means that, when the rotation angle varies, other solutions are obtained; consequently, other spinor deformed algebras are obtained. For future works on this matter, it is possible to propose the formalism of a general expression of the spinor partial differential equation. Using this formalism, it is possible to formulate another kind of relativistic wave equation as spinor representation substituting a = −iℏc, b = mc ² y f = E, obtaining

and its interpretation in their solutions. It is important to consider that this formulation was done without deformation. Other suggestion for further work, is the problem of describing the q-relativistic wave equation

for some Minkowskian-valued spinors

and is subject to Pauli matrices in the Minkowskian space proposed in [¹].