Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ensayos sobre POLÍTICA ECONÓMICA
Print version ISSN 0120-4483
Ens. polit. econ. vol.28 no.spe61 Bogotá June 2010
On the social value of banks
Sobre el valor social de los bancos
Sobre o valor social dos bancos
George McCandless*
*This paper has benefited substantially from discussion with Julio Elias. Research Department.
Central Bank of Argentina E-mail: catbirdsouth2000@ yahoo.com
Document received: 27 February 2009; final version accepted: 20 October 2009.
I compare the utility of individuals in an economy with and without banks. To make the comparison interesting, the economy without banks has cashin- advance money that the individuals use for consumption and for precautionary (emergency) purposes and that firms use to pay their wage bill. In the economy with banks, the precautionary funds are deposited in banks, which lend this money to firms for working capital. In these economies output is generally higher, people have higher utility and live longer. Also, the price level is usually higher.
JEL classification: E4, G2.
Keywords: wage, money, interest rates, financial institutions and services.
Comparé la utilidad de las familias en una economía con y sin bancos. Para hacer interesante la comparación, la economía sin bancos tiene dinero, tipo cash-in-advance. Las familias usan dinero para el consumo y para sus emergencias, y las empresas lo usan para pagar los salarios de sus trabajadores. En la economía con bancos, los ahorros para emergencias se depositan en los bancos y los bancos prestan estos fondos a las empresas.
En general, en economías con bancos, el producto es más alto, las familias tienen más utilidad, y la gente vive durante más tiempo. El nivel de precios es más alto en la economía con bancos.
Clasificación JEL: E4, G2.
Palabras clave: salario, dinero, tasas de interés, instituciones y servicios financieros.
Comparei a utilidade das famílias em uma economia com e sem bancos. Para fazer interessante a comparação, a economia sem bancos tem dinheiro, tipo cash-in-advance. As famílias usam dinheiro para o consumo e para as suas emergências, e as empresas o usam para pagar os salários dos seus trabalhadores. Na economia com bancos, as poupanças para emergências são depositadas nos bancos e os bancos emprestam estes fundos às empresas.
Em geral, em economias com bancos, o produto é mais alto, as famílias têm mais utilidade, e a gente vive durante mais tempo. O nível de preços é mais alto na economia com bancos.
Classificação JEL: E4, G2.
Palavras chave: salário, dinheiro, taxas de juros, instituições e serviços financieros.
I. Introduction
The classic model of banks is that of Diamond and Dybvig, 1983. This vision of banks describes how they can provide liquidity to an economy while permitting the financing of longer term projects. The model is beautiful in its simplicity: families save in the initial period; some discover that they only get utility from consuming in the next period while the rest can wait another period before receiving the returns on the long-term projects. The model allows considering bank runs since there exists a second Nash equilibrium in which banks are run. However, the long-term projects that make the Diamond-Dybvig model work are not that much like what banks really do. Most bank lending is relatively short-term.
In this paper I consider a pair of economies where individuals have liquidity (or precautionary savings) needs. In each period, some randomly chosen fraction of the households will experience an emergency, and hire emergency services to increase their probability to survive the emergency. Both goods consumption and emergency services must be financed with cash-in-advance money. Because of the possibility of having emergencies, households hold precautionary savings either as money, in the baseline economy, or as deposits, in the version of the economy with banks. In the economy with banks, firms can borrow from the banks to finance their working capital, while in the version without banks firms must hold money from the previous period to use as working capital. By comparing the expected discounted welfare of households in this economy, with or without banks, I provide a way of evaluating the social benefits of banking activity.
By definition, banks take in deposits from the public and make loans. The types of deposits they take in are mostly short-term: sight deposits or certificates of deposit of a year or less. The loans they make are longer term than the deposits, but most commercial loans are relatively short-term. In August 2006, of $106 trillion in commercial loans by US banks, only a bit over $6 trillion had maturity of more than a year1. Regarding farm loans from commercial banks made in the week of August 4 to 8, 1986, the data I have available, 85.5% of their value went to working capital (animals, operating expenses), 7.9% to machinery and 6.6% to farm real estate. The weighed average maturity of all these loans was 8.8 months. Although many of these relatively short-term loans may be regularly rolled over, these numbers suggest that the major portion of commercial bank lending is not very long-term. One of the reasons that evaluating the benefits from banks is important now is that, as happens during almost every financial crisis, there are renewed calls for Simons’ banks. Simons’ banks are equivalent to the economy described in this paper without banks2. Most formations of Simons’ banks do not allow banks to exercise commercial lending, but rather restrict them to invest only in very safe and liquid assets, usually short-term government domestic currency bonds. Every time Simons’ banks are brought up, the benefits that they provide by protecting the payments system is the point of focus. However, Simons’ banks do not come without costs, which are those resulting from prohibiting the banks to do what banks do in this paper: commercial lending for working capital purposes.
The type of economy considered here generates two benefits from adding banks. First, because the banks lend at interest and, as mutual banks, pay this interest to their depositors, there are incentives for the families to hold more precautionary savings and, therefore, to be able to finance more emergency services and have higher probabilities of surviving the next period. Since the unused precautionary savings are available to the banks to be lent to the firms, firms pay a lower cost for working capital and use relatively more of it. This lower cost results in higher output in the economy with banks.
For the comparison of the two economies to be interesting, they need a number of features. In the version without banks, both households and firms face cash-inadvance constraints. Households hold money for normal consumption purposes and to cover random large liquidity needs. The liquidity needs used here can be thought of as a medical emergency where medical services need to be hired; the more medical services purchased, the higher the probability of surviving the emergency. The advantage of using this kind of service is that the costs of the service automatically adjust to the cost of hiring labor. Firms need to hire and pay labor before they sell their goods. They need either saved or borrowed money to meet their wage bill.
In the economy without banks, a substantial fraction of the money stock does not participate in transactions in each period. Some funds are held for precautionary purposes and households that do not experience any kind of emergencies do not spend all of them. The amount of money held by each family is equal to the cost of goods consumption and the purchase of emergency services by a family that experiences an emergency. Those who do not face an emergency have redundant cash. In the economy without banks, firms hold cash between periods to cover their wage bill. With banks, the excess liquidity of the households can be lent to the firms for their working capital needs. One of the main activities of commercial banks is to use excess household liquidity to make short-term loans to firms. That is what banks do in this paper.
The banks that are added to this economy are very simple banks. They are oneperiod banks, lending after both the emergency and technology shocks are realized, so they bear no risk. Households hold money from the previous period. Some households use part of that money for their emergencies and the rest deposit the money in the bank. The bank then lends to firms for working capital. In a stationary state without money issue, the gross interest rate that banks can offer on deposits cannot go below one, so there can be cases where not all of the money that is deposited in the bank gets lent out to the firms.
An interesting set of results comes from this model. Introducing banks into the economy tends to (but does not always) increase output, consumption of goods by both those with or without emergencies, hiring of labor to produce more emergency services, and survival rates (and therefore life expectancy); it also generates a jump in the price level and real wages go up. Under the best conditions, introducing banks raises the return that households get on holding money for precautionary needs and provides funds to the firms at an interest rate lower than the implicit interest rate that comes from the firms’ discount rate. The reduction in the interest rate paid by firms means that they hire more labor and drives up the wage rate. This means that the cost of emergency services has gone up, and whether more or less emergency services are hired depends on whether the income effect of the higher wages dominates the substitution effect caused by labor becoming relatively more expensive. Prices are higher with banks because more of the money stock is involved in transactions in each period (some or all of the precautionary savings that is not used for an emergency is now used by the firms to pay wages).
The rest of the paper proceeds as follows: section 2 describes the model with three cash-in-advance constraints; section 3 adds banks with in-period lending to the money economy; section 4 gives the results for some calculated stationary states, and section 5 concludes.
II. The economy without banks
We begin by constructing the economy without banks, and then add banks to that economy. Households and firms face cash-in-advance constraints; in consumption and emergency purchases for the households and in the wage bill for the firms. Without banks, both households and firms need to carry money over from the previous period. In this economy, not all money will be used for purchases in each period since the households that do not experience an emergency will have precautionary money holdings that they will not need to use.
A. Households
There is a unit mass of individuals in the economy. A fraction, ρ(1 − p(hx t )) of them die each period and is replaced by and equal number of live, but otherwise identical, individuals who inherit their wealth, kt+1 + mt+1/ Pt . . The probability of surviving the emergency, p(hx t ),, is determined by the amount of emergency services, hx t ,, that a household hires. The workers who provide emergency services receive the same wage as workers who produce goods.
At the beginning of each period, a household discovers if it has an emergency or not. With 1 − ρ probability a household does not require the emergency liquidity (nl) and faces the decision problem:

subject to:

and the cash in advance constraint:
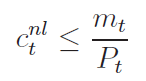
Here, kt is the capital carried over from the previous period, mt is the money carried over, cnl t is the goods consumption, hnl t is the labor supplied, πt are the lump sum dividend payments from the profits of the firms, and ψnl t is a lump sum tax or transfer that will make all surviving families have the same wealth at the end of each period. The depreciation rate is δ, the wage rate is wt, the rental rate on capital is t, and the price level is Pt..
With ρ probability a household has to finance some emergency expenditure, which in turn determines the probability that they will make it to the next period. Think of it as if they got sick, and had to pay for medical bills, which is why the probability is a function of the labor they hire. The decision problem of those with liquidity needs (l) is:

subject to the budget constraint:

and the cash in advance constraint:

This cash-in-advance constraint says that the household will pay wthxt for medical services and will still consume cl t . The amount of medical services they hire is monotonically related to the probability that they will survive into the next period.
To keep the model simple (and be able to aggregate the results), we add a lump sum transfer program so that kt+1 + mt+1/pt is the same whether one has a liquidity demand (and lives) or not. Lump sum taxes for those who do not have liquidity demands are ψnlt . and the lump sum transfer to those who do it is ψlt . The transfer program has a balanced budget, so:

Since the probability of death in any period is ρ(1 − p(hx t )),, life expectancy of a person alive at the beginning of period t (before the liquidity need is revealed) is:

which, if one is in a stationary state, hx t+i−1 = hx,, is:

since ρ(1 − p(hx)) is strictly between 0 and 1.
1. First order conditions
Since it is a bit unusual to solve models where the discount factor on the recursive part of the problem is a function of choice variables, I show the first order conditions. For the problem of a household that does not suffer a liquidity need, they are:

and the expected values of the derivatives of the value function for those without the liquidity shock (from the envelope conditions) are:
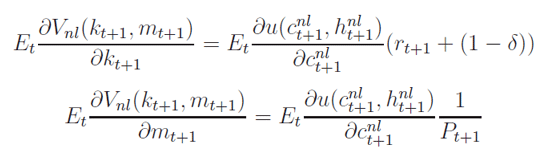
Those without the liquidity shock face the budget constraint:
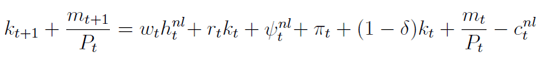
where the cash-in-advance condition (which is usually non-binding) is:
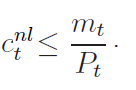
The first order conditions for a household that does suffer a liquidity need are:

and the expected values of the derivatives of the value function for those who do suffer a liquidity shock (from the envelope conditions) are:

Those who suffer the liquidity shock face the budget constraint:

and the binding cash in advance constraint:

The main difficulty we have when using these first order conditions is that they contain the value functions for both those who do and those who do not face the liquidity constraint. In general, we do not know the value function.
B. Production
There is a unit mass of identical, competitive firms. The goods production side of the economy can be expressed by the Cobb-Douglas production function:

where the equilibrium conditions for capital and labor are:

and

and where At is the time t technology level.
Firms have a cash-in-advance constraint in that they need to hold cash from the previous period in order to cover their wage bill. Define mf t as the money that a firm has carried over from period t − 1. Let ∫ 1 0 mf t = Mf t . The budget constraint of the firms is:

subject to the cash-in-advance constraint:

Firm managers maximize:

and if the rate of gross inflation is not less than β, the cash-in-advance constraint holds with equality so that:

The first order conditions that we get from the firm managers’ decision are:
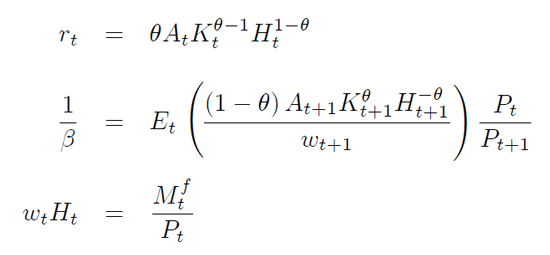
In a competitive economy, because of the effects of having to hold money over from the previous period, profits will be:

Using the first order conditions on rentals, we have:

The condition for rentals is:

C. Equilibrium conditions
All of the non-liquidity constrained households are alike as are the liquidity constrained households. That means that;
Cnl t = cnl t
and
Cl t = cl t.
The insurance plan means that:
Kt+1 = kt+1
and
Mh t+1 = mt+1,
since both the liquidity constrained and the non-liquidity constrained end up with the same wealth and will allocate it in the same manner.
Market clearing conditions in each period for capital and labor are:

and, defining

and
Hx t = hx t ,
labor supplied to production is:
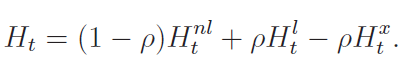
Define the aggregate money held by the households into period t + 1 as:

The total money held by the firms into period t + 1 is Mft+1. A constant money stock3, M, is equal to:
M = Mht+1 + Mft+1
As mentioned above, the zero profit condition for the insurance plan is:
0 = ρψ1t + ( 1 - ρ) ψ nlt
D. Stationary states
It is possible to find the value of the value functions in a stationary state. By imposing the stationary state conditions that kt, mt akntd, mt are constant through time, we know that:
Vi = Vi (kt,mt) = (k t+1,mt+1)
for both i = l and i = nl.. In addition, because of the insurance program, the liquidity constrained households that survive, the new households that replace the liquidity constrained who die, and the non-liquidity constrained households have the same stock of capital and the same money holdings. The discounted value of lifetime utility in a stationary state can be written as:

for the liquidity constrained, and as:

for those who do not face the constraint. The other first order conditions see that the values of Cl, Hl and Cnl, Hnl are those which meet the conditions for a maximum.
The sub-utility function we use is:
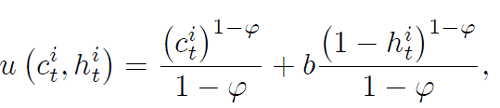
for i = l, nl, with 0 < φ < 1.. The function, p(Hx t ),, which gives the probability of living if one has a liquidity constraint as a function of the services hired, is:

where a > 1.
In the aggregate stationary state version of the model the equations that come from
the first order conditions of the households are:
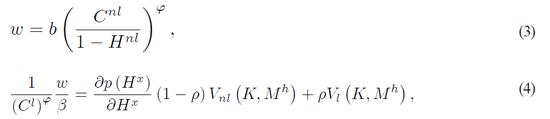
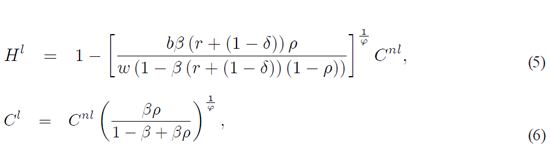
and

The aggregate, stationary state version of the non-liquidity constrained household’s budget constraints is:

and the budget and cash-in-advance constraints for the liquidity constrained households are:

and

The stationary state version of the production function is:

where

The first order conditions for the firms are:

Profits in each period are:

Notice that with this level of profits, the value of the firm at time t, once the time t dividends have been paid is:

which is equal to the amount of money that the firm is carrying over to the next period to cover the wage bill. If the firm closed in this moment, this is exactly what it would be worth.
Two equilibrium conditions are the distribution of money;

and the zero profit condition for the insurance plan;

The full set of 18 stationary state variables is

The set of 9 parameters of the model is

The equations for the stationary state version of the economy without banks are given in equations 1 to 18.
III. Banks with in -period deposits
We add a simple bank to the previous model. In each period, those who do not have an emergency deposit the money they are not going to use for consumption into the bank. The bank lends this money to the firms to help cover the wage bill. The banks are mutuals, and so all interest paid by the firms is passed along to the households.
A. Households
Households maximize the same discounted utility function as in the previous section. However, the budget and cash-in-advance constraints are different. The households without emergencies maximize subject to the budget constraint:
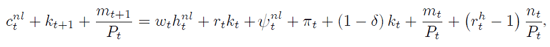
and the cash-in-advance constraint:

Instead of holding excess money, households deposit all the money they are not using for consumption into the financial system and receive the gross return rh t on those deposits.
Households with the emergency expenditures maximize subject to the budget constraint:

and the cash-in-advance constraint:
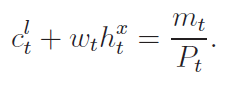
Their entire cash holding is used to finance consumption and the services that they pay for in case an emergency occurs. Since, as we will see, capital pays a higher return than bank deposits, households will hold only the amount of money they need to cover their desired expenditures during an emergency.
The first order conditions that come from the households’ maximization problem are:
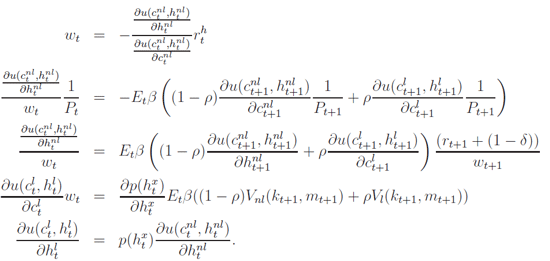
along with the four constraints:
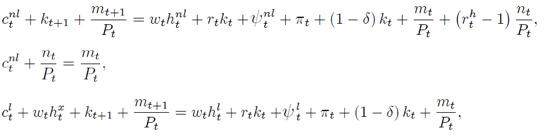
and

There are some corner conditions here. If the expected interest rate paid by the banks becomes less than rh t = 1,, all households will hold only money, since, with a constant money supply, the expected rate of return on money will not fall below that amount.
B. Banks
Banks take in the deposits of those who do not have emergencies and lend these funds to the firms to cover all or part of their wage bill. Banks make no profits (they are mutuals) and lend at the same rate that they borrow from the depositors. Banks do not make loans to individuals who have emergencies. They only make riskless in-period loans to firms. Since only those without emergencies deposit in the banks, total deposits available to the firms are:
N t = ( 1 - ρ) nt.
Banks lend these at the rate rf t = rh t. Banks lend all the deposits they receive to the firms.
C. Firms
If the interest rate on borrowing from the banks is less than 1 / β, their cost of holding money, the firms will borrow as much from the banks as they can. That is, Nt = (1 − ρ)nt. The firms will save from the previous period Mf t to cover the expected difference between their borrowings and their desired nominal expenditure on labor. The aggregate cash in advance constraint for the firms is:
Nt +Mft = PtwtHt.
The firms are maximizing the value of the firm:

subject to the budget constraint:

and the cash-in-advance constraint. The production function is as before:

First order conditions for the firms are:

The last conditions is with inequality if Mf t = 0, if the firm can borrow from the banks all of the funds it needs to finance the wage bill. If it cannot borrow enough, then Mf t > 0, and the condition is an equality (which implies that in a stationary state without inflation, ¯rf = 1/β).
D. Equilibrium conditions
Most of the equilibrium conditions are the same as those in the economy without banks. The major differences are in the conditions for the banks, which we assume are competitive and therefore lend all the deposits they receive if the interest rate that the firms pay is greater than rf t > 1.
E. Stationary state
We use the same sub-utility function and probability function as in the no-bank economy.
The equations for the stationary state with banks that are different from the no-bank economy are:

The labor costs to the firms is:
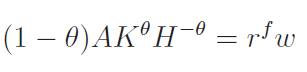
where rf = rh.
Using the cash-in-advance constraints for the non-liquidity constrained households, as:

along with:
N = (1 − ρ)n
to get:

Combine this with:
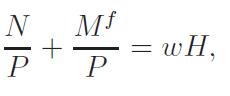
to get:

add that:

and we have that:
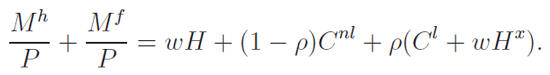
Since we have a constant money supply equal to 1, Mh t +Mft = 1,, we have that:

For the households, we have that:

and:


and
π = 0
otherwise rf = 1/β , and
Mf = PwH − N
and

From the household budget constraints, we have that the transfers are:

and:

with the equilibrium condition that:

The full set of 20 stationary state variables is:

The set of 9 parameters of the model is:

The two variables added in the economy with banks are the interest rate, rf, and bank deposits, N.
IV. The results
Table 1 shows the calculated results for the variables in stationary state equilibrium, both with and without banks, when the parameter values are β = .9, φ = .8,b=1. 2, a = 4, α = .1, ρ = .1,θ = .4, M =1 and for a set of values for A = {1, 2, 3}.. Real GDP is calculated by adding the real value of goods output to the real value of emergency services, GDP = Y + wHx
Comparing the results with and without banks in Table 1, one can point to a number of interesting differences. First, with the parameter values used, both output and probability of survival are higher when the economy has banks. The increased returns that households get from bank deposits over cash increase precautionary savings, and this reduces the probability of death. The reduced cost of financing for firms (since the interest rate is below the firms’ discount rates) causes them to hire more labor and therefore increase output. For both of these results to occur, the bank interest rate needs to be above 1, so that it offers a better return than cash to the households, and below 1/β so that it is cheaper for the firms than holding cash between periods. A certain tension exists between increased savings for precautionary purposes (with the accompanying increased probability of surviving an emergency) and goods output. If increased savings increases the demand for emergency labor services sufficiently, this can reduce the amount of labor available for goods production and end up reducing output.
The most reasonable measure of utility for this model is the expected value of lifetime discounted utility at the beginning of a period (before a family knows if it has an emergency or not). In a stationary state, this expected lifetime utility is equal to:
(1 − ρ)Vnl + ρVl,
and, for our example economy, the values are given in Table 2. As can be seen, expected lifetime utility (the expected value of the value function) is higher with banks. This comes from the combined effects of higher output in the economies with banks, and from the higher probability of surviving into the next period forthose with emergencies that occurs because of banks. The effect on expected utility that comes from increased life expectancy is relatively small in this example because the probability of having an emergency is relatively low. In Table 1, comparing the rows for Vnl and Vl shows that adding banks changes the expected value of lifetime utility for those who have an emergency substantially more than adding banks does for those who do not have an emergency.
Note that the economies with banks have higher price levels than otherwise identical economies without banks. This occurs because a substantial fraction of money does not enter into circulation in the economy without banks: much of the precautionary savings of the households who do not have an emergency is hoarded and does not enter into circulation during the period. In the same economy with banks, these deposits are lent to the firms and are used to pay for working capital. Since the firms need to hold less cash, households hold relatively more for consumption and precautionary purposes and this results in a higher nominal price for the final good.
IV. Conclusions
The model presented in this paper is a general equilibrium example where the intermediation services of banks are welfare improving. The banks in this model represent the kinds of banks found in many countries where banks do not provide services for capital investment but mostly provide funds for working capital. In the model in this paper, capital investment happens outside of banks. The cash-in-advance constraints of this paper see three uses for money: for household consumption purposes, paying the firms’ wage bill, and covering the costs of a family emergency that can affect the survival of members of the household (an illness, for example). In general, the equilibrium with banks results in increased output, consumption of goods, and emergency services, and in higher utility for the households. These results can depend a bit on how sensitive the demand for emergency services is to increased savings, so that it is possible to find an equilibrium where the probability of survival increases and goods output declines. However, adding banks always increases household welfare.
Technically, the use of three cash-in-advance constraints is interesting, especially since in the economy without banks the entire money stock does not change hands each period. In addition, making survivability an endogenous choice presents some interesting problems to solve for the stationary states.
This paper does not try to compare the relative benefits of reduced risks to the payments system that a Simons’ bank would provide with the welfare costs that such a system imposes. What is given here is a clear way to consider what the welfare costs of imposing such a system might be.
comentarios
1 See www.federalreserve.gov/pubs/supplement/2006/08/table4_23a.
2 Named after Henry Simons, who, along with other University of Chicago economists, proposed such banks in a 1933 memorandum "Banking and Currency Reform". For a discussion and a copy of the memo. see Phillips, 1995.
3We are not considering the effects of inflation in this paper.
References
1. Diamond, D.; Dybvig, P. "Bank Runs, Deposit Insurance, and Liquidity", Journal of Political Economy, vol. 91, no. 3, Chicago, University of Chicago Press, pp. 401-19, 1983. [ Links ]
2. Kiyotaki, N.; Moore, J. "Credit Cycles", Journal of Political Economy, vol. 105, no. 2, Chicago, University of Chicago Press, pp. 211-248, 1997. [ Links ]
3. Phillips, R. J. "The Chicago Plan and New Deal Banking Reform", M. E. Sharpe Inc, Armonk, NY, 1995. [ Links ]