1. Introduction
Port terminals are a basic node in global transport networks, so all operations of these networks must be optimized in order to achieve maximum overall productivity in this network node (Ambrosino, Sciomachen, and Tanfani, 2004). Among the different types of port terminals, the two main groups are terminals specialized in a single type of cargo and multipurpose terminals that handle more than one type of cargo.
Since the twentieth century, different events have taken place that drastically accelerated the evolution and development of container ports. Among the most important is the appearance of the container in maritime transport, which significantly reduced loading times and costs, causing a decrease in freight rates and thus an increase in the flow of business. This has led to an increasing number of specialized container ports, also known as Maritime Container Terminals (MCT), which have resources, machinery, and facilities adapted to handle containers efficiently.
These MCT are complex logistics systems since different operations are carried out simultaneously internally, such as unloading of ships, the inspection of goods by authorities, storage of containers, loading of export goods, transport of containers to designated spaces, etc. Different authors have divided the operations of the MCT into subsystems, which allows better use of resources when proposing management models, this is because the diversity in the machinery that is used for its operation and the variable amount to be addressed per operation is very large thus turining port systems into complex logistics systems. It should be borne in mind that the operation of each terminal depends on its design, which in turn depends on factors such as size, type of goods handled, etc. In the literature, we find research such as those by Steenken, Voß, and Stahlbock, (2004) and Stahlbock and Voß (2007) in which the authors collect the main works related to the handling of containers. The authors group the works according to the subsystem of the terminal which they address in order to propose improvements.
One of the most important operations in MCTs is the internal transport of containers, which handles the horizontal transport that mobilizes containers throughout the terminal, and the transport for stacking of containers carried out by the cranes. According to Ramírez-Nafarrate, González-Ramírez, Smith, Guerra-Olivares, and Voß (2017), horizontal transport is subdivided into pier transport and land transport serving ships, external trucks and trains respectively. Thus, these specialized vehicles or trucks are moving through the terminal constantly, which in addition to those arriving from within the country, generate large congestion within the MCT (Jovanovic, 2018).
This research proposes a model for the management of internal transport that considers three strategies called single cycle, double cycle and mixed cycle, with the aim of minimizing the empty journeys by trucks within a seaport. The first section presents the theoretical framework that synthesizes the most relevant works that propose models to manage this process, then explains the methodology used for the formulation of the model, as well as its functioning which gives way to the results obtained, to close up with the conclusions and the list of references.
2. Theoretical framework
Below are the papers and research that were consulted for the preparation of this research. These documents allowed to argue the importance of the problem addressed, as well as the relevance of the tool used.
2.1. Management of internal transport in seaports
Internal transport in seaports, also known as Landside transport, is the operation where all container movements are planned in a container port. A container usually spends seven days on average in a maritime container terminal (World Bank, 2019), from the day of arrival to just before departure. Container movements are carried out to allow the development of activities such as customs inspections, unpacking of cargo, relocation of empty containers, etc.
The management of land transport is focused on different points of view in the literature. Research such as Chao (2002) and Scheuerer (2006) propose a variation of Vehicle Routing Problem (VRP) to truck routes, which generates the Trailer Routing Problem (TRP). The goal is to minimize distances within the terminal. This proposal has served as a basis for the development of research such as those of Jula, Dessouky, Ioannou, and Chassiakos (2005), Mattfeld and Orth (2006), Namboothiri and Erera (2008) and Caris and Janssens (2009) that model the transport of containers within the terminal with the aim of minimizing costs and distances.
Other research focuses on the handling of only certain ground transport machinery as in Corry and Kozan (2006) and Hansen (2004) that manage land transport carried out by trucks with more than one platform (truck-rail). Zehendner, Rodriguez-Verjan, Absi, Dauzère-Pérès, and Feillet (2013) and Das and Spasovic (2003) propose a procedure for the assignment of straddle carriers to trucks to perform the operation of loading and unloading containers.
Authors such as Zhen, Yu, Wang, and Sun (2019) have studied the relationship between truck programming and dock cranes. These authors propose a mixed integer optimization model that is solved with the CPLEX tool. The proposed model allows the planning of both resources under a cost-minimization approach.
As explained above, to manage land transport some research focuses on it as a VRP-type vehicle route problem within the MCT. Among these investigations is the one conducted by Nishimura, Imai, and Papadimitriou (2005) wherein the authors approach internal movements as a problem of truck routes in the esplanade of a MCT. They are based on the fact that the optimization of these routes reduces the distance of journeys made by trucks from one point to another in the terminal. They do a variation to the VRP, which is the VRPB acronym for vehicle routing problem with backhauls, which corresponds to the problem of vehicle routes with return routes. When solving the VRPB, we find an optimal set of delivery and collection sequences of containers in which the vehicles start from a particular point.
These authors propose a model to optimize the routes of trucks that move container between the storage area and the docks. This model allows optimizing the routes to and from different points located anywhere in the terminal. Figure 1 shows the location of three delivery points which correspond to one for each ship and nine collection points distributed within the terminal. Solving the problem results in a sequence of routes that will connect the twelve pick up and drop points.
2.2. Management of docks transport
To carry out loading and unloading operations of the containers on the ships, it is necessary to transport containers from the different blocks in the Storage Zone (SZ) to the cranes assigned to each vessel. This operation is called dock transport and good management will allow gantry cranes to perform their work efficiently. In the scientific literature, this problem is often referred to as Quayside Transport Planning (QTP). This area of the terminal is known as a buffer and it is necessary to optimize transport in it because:
Synchronization of horizontal transport vehicles with gantry cranes prevents the generation of idle times and bottlenecks.
Route design can eliminate possible traffic jams in the dock area.
Horizontal transport vehicles are constantly used throughout the MCT so their optimal allocation allows for a good overall operation.
The efficiency of container loading and unloading operations performed by gantry cranes directly depends on the efficiency of dock transport.
In recent times transport between the shipping area and the SZ has been done by self-guided vehicles better known as Automated Guided Vehicles (AGVs). These vehicles are more efficient than flatbed trucks or front-handling equipment at handling containers. In the literature, we find work such as Ho and Hsieh (2004), Ho and Chien (2006), Grunow, Günther, and Lehmann (2004) and Yan, Zhu, and He (2014) that evaluate the benefits of MCT automation with this type of vehicles, but also identify that these depend on other machines to perform their work.
To obtain the maximum performance from this type of vehicle, high investments must be made on facilities, software and equipment necessary to incorporate them into the operation of the terminal. All this is beneficial to MCT as long as there is a good flow of containers. Günther and Kap (2005) compiled works where the different situations of optimization of these types of vehicles are studied in order to achieve their maximum performance.
There is another type of self-guided vehicle known as ALV (Automated Lifting Vehicle) which can lift containers from the ground without needing assistansce by other handling equipment. In works such as Nguyen and Kim (2009), Vis and Harika (2004), and Yang, Choi, and Ha (2004) comparisons are made between AGVs and ALVs in automated container terminals, and in most studies, ALVs display higher performance when engaged in dock transport tasks.
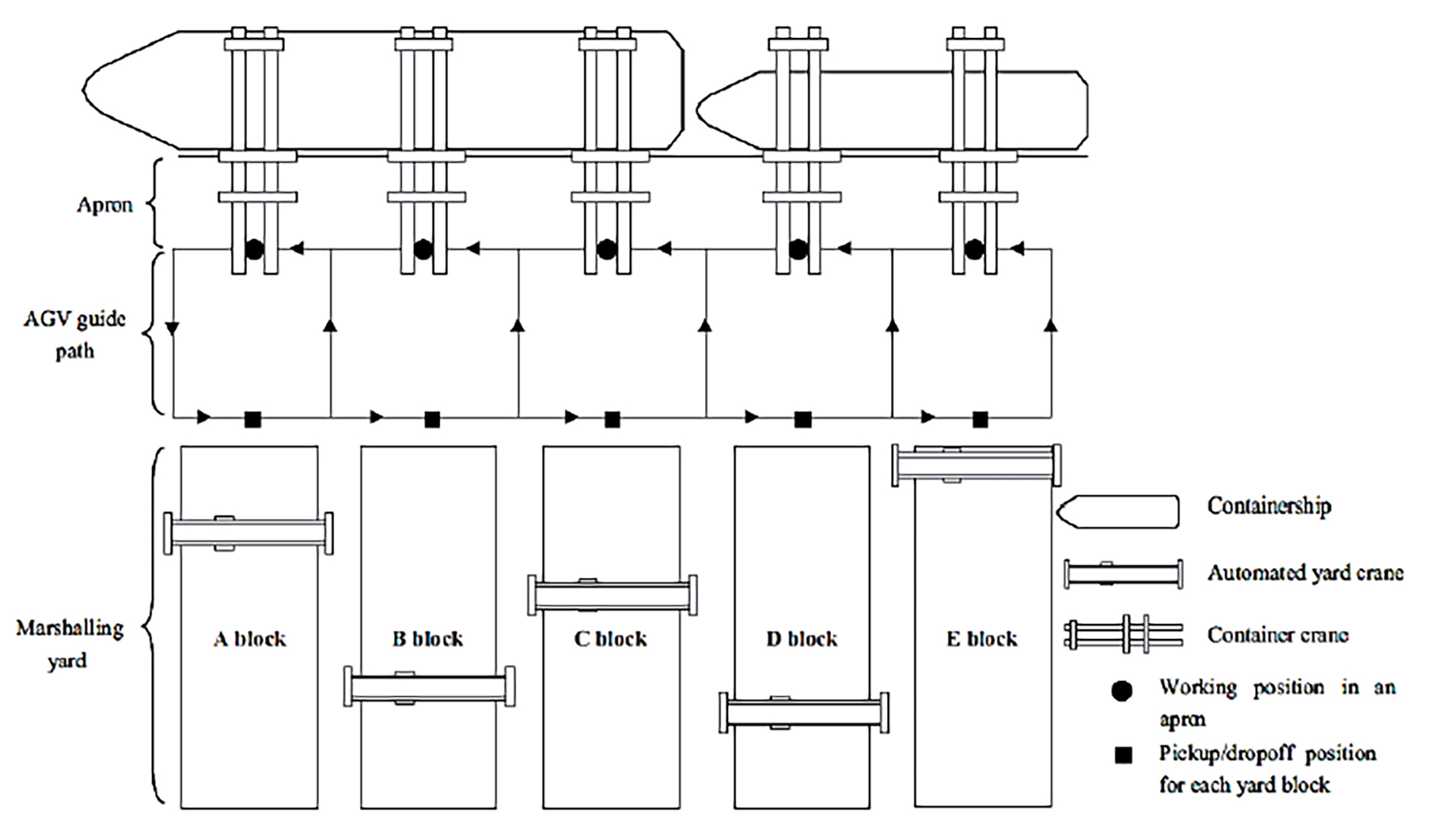
In Figure 2, taken from Kim and Bae (2004), there is an example of an MCT in which the transport in docks is carried out by AGVs, and as supported by the above considerations the handling machinery involved are the dock cranes, the esplanade cranes and the AGVs, the circles and the black squares represent the points at which the AGVs deliver or receive each container by the respective crane.
For the elaboration of the model, the authors make other more specific considerations listed below:
Each AGV can be assigned or served to more than one dock crane.
All AGVs are the same and can only transfer one container at a time.
The waiting times of AGVs under the esplanade cranes are not considered.
The times it takes for a dock crane to drop a container on or take it from an AGV are negligible.
Congestions that can occur between the different routes by the AGVs in the transfer operations are not considered.
2.4. Simulation as a tool for managing seaports operations
The use of simulation models for the management of seaports is very common, some authors such as Silberholz, Golden, and Baker (1991) propose a simulation model to evaluate the impact of ships loading and unloading strategies on the productivity of MCT. The authors focus mainly on compliance with the time of service to ships according to their time of arrival. This work demonstrated the potential of simulation as a methodology that not only evaluates the efficiency of ports but also allows to evaluate the efficiency impacts that would generate possible tactical or technical changes such as the automation of port operations, which has been widely addressed by such authors as Ahmed (2014), Gharehgozli, Vernooij, and Zaerpour (2017), Jula and Ioannou (2002), Liu, Jula, and Ioannou (2001) and Yang, Choi, and Ha (2004).
The possibility provided by the simulation of assessing the performance of an entire port, identifying the main bottlenecks that limit total productivity and evaluating the impacts of possible solutions to be implemented, made this methodology one of the most widely used in different regions throughout the world. In some works, to evaluate the efficiency of the entire port and its resources, such as Nam and Yu (2002) applied to the MCT of Pusan in Korea; Zhou, Guo, and Song (2007) who design a simulator that includes algorithms for decision-making; Beškovnik and Twrdy (2010) where they use simulation to plan, organize and evaluate the efficiency of an MCT; and Nicoletti, Chiurco, Arango, and Diaz (2014) that through a simulation model evaluate the performance of the machinery in a Spanish MCT.
Another approach within simulations, that every day has more applications, is that in which a model is drawn up for the management of a specific activity or resource, but considering elements of the environment that affect its performance, an approach on which this research is based. Authors such as Ho and Chien (2006) and Soriguera, Espinet, and Robuste (2006) evaluate the management of vehicles for the internal transport of containers; Lee, Cao, and Shi (2007) and Legato, Canonaco, and Mazza (2009) evaluate and optimize the operations of dock cranes and gantry cranes; Arango, Cortés, Onieva, and Escudero (2013) and Arango, Cortés, Muñuzuri, and Onieva (2011) evaluate and optimize the allocation of docks and wharf cranes to ships.
3. Simulation-based methodology for the management of internal transport in a seaport
This section explains the design and operation of the simulation model which has two important purposes, firstly, the simulation of the port system’s complexity when considering the internal requests that are made for trucks to support all internal transfers of the MCT, and secondly, evaluating three transport strategies on esplanade called: single cycle, mixed cycle and double cycle. Three integrated sub-models are available to meet these purposes, which are explained below. The software used to design the simulation model is Arena 14.0 which has a powerful compiler and great versatility to model any type of process.
3.1. Ship Arrival and Data Reading
The largest flow of containers and thus of tasks to transport them is generated when a ship arrives at the port, which is why the model focuses mainly on the management of internal transport between the dock and the storage area. For this purpose, a submodel was designed and represents how ships arrive at the port and go to the dock assigned for the loading/unloading of containers. The most important modules in this submodel are shown in Figure 3 and among these, the Create module, known as “Ship Arrival”, stands out, where the ship entities (entity 1) are created. The attributes and variables are then declared, using a Readwrite module which takes the data from an Excel file (where the data necessary for the execution of the simulation is).
With regard to travel times between the dock and the locations of the different containers in the storage zone, the maximum time was set at 4 minutes for the simulation model. To determine this, an MCT of 100 hectares and loading time for cranes of 1 minute was considered.
For the simulation model, six virtual docks have been created to perform container loading and unloading operations, this in order to represent possible congestion in the berthing line. Simple modeling is used with a Decide module, in which a free dock is sought. This is done by a variable called Route, which the Est_Muelle state vector (6.1) traverses. The Est_Muelle vector represents the state in which each of the 6 docks is. In case there is no free dock, the ship will go to a Hold where it will wait for a dock to become available.
3.2. Cycle Assignment
This submodel identifies the type of cycle with which the internal containers transport tasks that will be carried out, for which there is a set of modules divided into three groups which are presided by the Choose module, whose function is assigning the type of cycle, and subsequently the rest of modules assign the attributes and variables that represent the operation. The ICLOI attribute, where the letter I indicates the location of tasks such as a crane. QI (I) and QE (I) attributes are also used. Within each set of tasks to represent containers according to export or import, QI (I) will be assigned to QI (JI), indicating the location of the task. The GRUASJ attribute is also identified, which indicates the number of cranes to be used to unload the vessel at the dock J.Figure 4 shows the modules that perform cycle mapping.
Each time a sheep entity among these modules is subjected to an assessment of conditions to assign it the cycle that best suits it, which is why in Figure 4 there are three subsets of modules which correspond to each cycle. Figure 5 shows the routes according to the type of cycle.
Cycles are intended to minimize empty trips between tasks assigned to each truck. This strategy seeks to minimize the costs associated with the movement of trucks to transport containers from the dock area to the storage area, for this purpose three types of cycles are proposed. The ratio of costs per cycle is shown below.
CS Cost > CM Cost > DC Cost
3.2.1 Simple Cycle
When engaged in internal transport operations with a simple cycle-based programming, it is because a vehicle has two or more consecutive tasks assigned to it with the same origin point, for example, according to Figure 5 the vehicle must transport containers from point A to B and return empty to point A to continue the moves until the task set is completed.
3.2.2. Double Cycle
The dual cycle process differs from the simple cycle in that the truck does the processes in a sequence. That is, it unloads a container from the vessel (A) and moves directly to the storage area (B) where, in addition to unloading the container, it takes a second container to return to the starting point (A). When the tasks that can be performed under this method are finished, the model moves to perform internal transport under the simple cycle strategy.
3.2.3. Mixed cycle
This is the last type of cycle to be contemplated. The actions performed here set off in the simple cycle, with the premise that a vehicle can combine and share different points of origin and destination with other vehicles. Taking the ship unloading area as an example means that the same truck that loads a container into the crane (C) and unloads it into the storage area (A), then loads a container into the same area (A) to take it to the crane (B). This means that there are no routes in which the truck is empty and can also be combined with other types of cycles. The difference between the double cycle is that in this case, it works with the different cranes (in the double cycle it only worked with the same crane and did not interact with the others).
When two consecutive containers are not assigned to the same vehicle, the model encourages the management of internal transport under dual or mixed cycle, thus allowing for more efficient truck programming as a truck carrying a container can go to another port area for other operations to minimize empty journeys.
3.3. Simulation of complementary operations in the MCT
To complement the simulation model, operations that are constantly requesting trucks are modeled for activities such as transport of containers to inspection areas by customs authorities, relocation of containers to other available spaces of the SZ, transport of empty containers arriving at the MTC, etc. These constantly affect the availability of vehicles in the MTC. This submodel is shown in Figure 6, which is made up of a set of modules representing the trucks’ usage time, for this purpose requires the Hold modules mainly.
The objective of the simulation model is to take into account all the complexity and variability of the port system, thus generating a dynamic management strategy through the use of rolling horizons.
4. Results and analysis
Two different scenarios are contemplated to validate the proposed models, each scenario represents a period of 30 days and 12 replicas are prepared per scenario, equivalent to one year of operations; 24 replicas were prepared for scenario 2. This was done on a PC with a 1.3 GHz processor and 8 GB of RAM. Runtime was 30 minutes in total for all 12 replicas. The objective of Scenario 1 is to analyze how models with a workload of 159 ships behave over a period of 30 days. The objective of scenario 2 is to check the robustness of the models, making the unloading of the same 159 ships, but in half the time horizon (15 days). For both scenarios, three types of ships were contemplated according to the location of containers within the vessel; 35% of ships with a work section, 34% with two work sections and 31% with three work sections.
The proposed simulation model controls for the minimum number of trucks assigned to each ship is equal to the number of gantry cranes assigned to it, but with respect to the maximum, the model only controls that there is always a minimum number of trucks left to serve the potential vessels that could reach the MCT. Table 1 shows, for both scenarios, the percentage of times that a certain number of trucks were allocated to ships, for this purpose the number of work sections for each ship was considered.
Table 1 Allocations of vehicles to work sections on ships
| Work sections on ships | Number of trucks allocated in | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | |||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 35.00 | ||||||||
| 2 | 0.22 | 2.52 | 13.21 | 18.05 | |||||
| 3 | 3.96 | 11.95 | 4.40 | 5.66 | 5.03 | ||||
| Total | 35.00 | 0.22 | 2.52 | 13.21 | 22.01 | 11.95 | 4.40 | 5.66 | 5.03 |
| Scenario 2 | |||||||||
| 1 | 35.00 | ||||||||
| 2 | 0.21 | 2.55 | 15.72 | 15.52 | |||||
| 3 | 6.49 | 9.43 | 6.28 | 5.03 | 3.77 | ||||
| Total | 35.00 | 0.21 | 2.55 | 15.72 | 22.01 | 9.43 | 6.28 | 5.03 | 3.77 |
Source: Author own elaboration.
The table above shows the behavior of truck allocations according to the number of work sections on each ship. For ships with a single work section, the allocation was 4 trucks for all cases, this is because a single work section on a ship involves the assignment of a single crane and therefore all trucks must work under the simple cycle mode. This allows us to demonstrate that with a simple cycle transport strategy each crane needs four trucks to do the loading and unloading operations without generating bottlenecks.
Of the total number of ships considered in one month of operations, 34% correspond to ships with two work sections, of which 52% required 8 trucks, corresponding to 4 per crane, but the remaining 48% demanded between 5 and 7 trucks, this overall reduction of trucks per ship was derived from the use of the mixed cycle strategy. The foregoing occurred because after transporting a container from the dock to the storage area or vice versa a percentage of trucks was assigned to another crane to carry a container that was close to its last position, this was called mixed cycle and exceeded 30% of the movements in the second scenario. Table 2 shows the percentage of journeys that were made in each scenario by cycle type.
Table 2 Trips according to the cycle
| Cycle type | Scenario 1 | Scenario 2 | Average (%) |
|---|---|---|---|
| Simple Cycle | 74,5% | 67,2% | 70,9% |
| Mixed cycle | 25,5% | 32,8% | 29,2% |
| Total | 100,0% | 100,0% | 100,0% |
Source: Author own elaboration.
Table 2 shows that the mixed cycle strategy, despite being more efficient in terms of decreasing the number of vehicles per crane, which has a positive impact on the costs of the transport operagraption, only represented on average 30% of the trips, this is because the loading and unloading sequences of the containers affect the order in which they are transported, wherefore the management of internal transport requires both the simple cycle and the mixed cycle.
One of the purposes of the model was to reduce the activation of trucks for a few movements. Therefore, no condition was determined for the allocation of trucks to be balanced and thus to distribute the workload among available resources. This was done in order to identify if there were vehicles that were never assigned. Figure 7 and 8 show the number of containers each truck transported in Scenario 1 and 2 respectively, in addition to the average workload.
In scenario 1, 680 containers were transported per truck, a little more than in scenario 2 where the movements were 620; this because in scenario 1 trucks 44 to 50 were never used during the entire time-lapse and in scenario 2, despite the fact that all trucks 41 to 50 were used, 150 containers were mobilized on average in a month. Therefore, it can be concluded that the proposed model reduces the use of trucks, thus saving both equipment and personnel costs without impairing the performance of dock operations.
5. Conclusions
This work has focused on the management of dock transport, a very important operation in maritime container terminals since it supports the transfer of import and export containers from ships arriving at the port. Adequate transport management reduces congestion at the docks, reduces the waiting times of gantry cranes which are called dead times for this resource because they are unable to load or unload containers since there are no trucks available. Finally, it is worth noting that any improvement in the management of dock transport that reduces the number of trucks assigned to a ship, without compromising the productivity of the loading and unloading operation of the dock cranes, reduces the costs of this transport operation.
ARENA 14.0 was used as the simulation software tool, where the proposed simulation model was developed. This research allows corroborating that simulation is a methodology that permits considering aspects that mathematical models cannot alone. Thus, experiments provide results closer to reality, in addition to allowing the evaluation, adjustment and validation of management strategies in different scenarios before their actual implementation.
To validate the robustness of the model, two scenarios have been considered, which contemplate variations in ship traffic, the number of containers and variation in the number of trucks, among other variables, which has allowed us to appreciate the behavior of the model in the situations at hand.
The proposed model considers truck assignments per ship and not per crane, this approach allowed the implementation of transport strategies called simple cycle, double cycle and mixed cycle. The proposed strategies resulted in reductions in the number of trucks allocated per ship, in addition to reductions in the number of empty journeys. Mixed cycle journeys were on average 29% of the total, which allowed, in both scenarios, 50% of trucks to carry containers below average compared to the simple cycle.
With regard to the ratio of the number of trucks allocated by each crane and the working section of the ship, the model identified that the maximum number of trucks per crane is 4, with this number of trucks allowing cost reductions without affecting the productivity of the cranes. However, the mixed cycle strategy achieved reductions in the number of trucks per vessel when the vessel has more than one crane assigned to it. The results showed that a vessel with two cranes can work with 7 trucks and a vessel with three cranes can work with 9 trucks.
From these results, it can be concluded that the number of trucks allocated to a ship is directly related to the number of dock cranes assigned to the ship, the productivity of these cranes and the distance between the dock and the locations of the containers in the SZ. This case study considered cranes with a yield of 30 containers per hour, a MCT of 100 hectares and locations scattered throughout the storage area. In addition, two scenarios were designed to validate the model since in both scenarios the results were similar.
It has been proven that the simulation model developed is robust, since it contemplates situations that optimization models do not usually consider due to their variability, and it also allowed the validation of three strategies for the management of internal transport in an MCT. Given that this model does not provide for a balance in the use of trucks, for future research this simulation model can be integrated into an optimization model that allows the allocation and programming of trucks according to the criteria and policies of maritime container terminals.