Implementing FEM-DtN for an incompressible material on an unbounded domain

Liliana Camargo¹ and Jairo Duque²

¹ Mathematics, Universidad del Valle, Cali, Colombia. Universidad del Valle. lilicaz85@gmail.com.

² Dr. rer. nat., Universidad del Valle, Cali, Colombia. jjduque@univalle.edu.co.

ABSTRACT

This paper presents the implementation of the finite element method combined with Dirichlet-to-Neumann (D†N) mapping (derived in terms of an infinite Fourier series) for studying the solvability of an exterior problem arising in linear incomepressible 2D-elasticity. A reliable numerical experiment is also presented showing the accuracy of D†N mapping; only a few Fourier series terms were needed to get a good approximation to the solution. The stable Taylor-Hood element was used for finite element discretisation.

Keywords: mixed finite element method, Taylor-Hood element, D†N technique, linear elasticity, inf-sup condition.

Received: september 4th 2009

Accepted: november 15th 2010

Introduction

This article presents a procedure for studying the Galerkin approximation to an incompressible material on unbounded exterior domain Ω. This procedure used Dirichlet-to-Neumann mapping (D†N), (Han and Bao, 1997; Gatica, Gatica and Stephan, 2003; Kako and Touda, 2004), consisting of introducing an artificial boundary by drawing circumference Γ_R in R² with radius R in domain Ω; Ω was then divided in bounded part Ω_i and unbounded part Ω_R. Exact and approximate boundary conditions were given on artificial boundary Γ_R to solve the problem on bounded domain (Figure 1).

Figure 1. Domain Ω = Ω_i Ω_R and artificial boundary γ_R

Ω С R² was an unbounded and simply connected domain with Lipschitz continuous boundary Γ. Because of Dirichlet boundary conditions on space was defined. Hence, the problem of linear elasticity consisted in finding (u,p) ∈ so that:

Here u: Ω → R was the displacement and ?? was the pressure of a material subjected to some external force ƒ, µ > 0 was the Lamé constant and ε(u) the strain tensor given by for i, j =1,2. It was assumed for this material that the stress-strain ratio was valid for small deformations, as discussed in Necas (Necas 1986; Necas, 1981; Zeidler, 1988). It was supposed that force ƒ had compact support in this work and was defined inside region Ω_i.

Next, notation was adopted with norms L² (Ω) and H¹(Ω), respectively. Standard integration by parts led to the following variational formulation of the problem (1)

Notice that problem (1?) defined on unbounded domain Ω and Ω_i was the computational domain for the finite element method used here which was obtained by introducing artificial boundary Γ_R. The variational formulation of problem (1) in Ω_i had to be deduced next. Integration by parts was used, by virtue of stress tensor σ (u, p):= 2 με(u) - pI, where I was the identity matrix of R^2x2, this gave – div (σ(u, p) = 2μ div ε (u ) + grad p, leading to weak formulation.

Boundary integral was then analyzed. The next goal was to obtain one expression representing tensor σ (u, p) on artificial boundary Γ_R. The following decomposition of displacement u on unbounded domain Ω_R =

was then considered, where G₁ , G₂ and W were the harmonic functions to be determined. In particular, function ???? satisfied the following boundary-value problem

G_j is bounded, when r → + ∞.

Notice that values for G_j and u_jcoincided along Γ_R. Using the separation of variables method the following representations of G_j were obtained using Fourier series development

where coefficients a_n, b_n c_n and d_n were given by:

Using condition div (u)= 0 and representation (3) the following equation was obtained , and so .

Similarly, using the balanced equation in Ω_R, grad p = 2μ div ε(u) grad p = grad was obtained and hence Next could be estimated along Γ_R. To this end, it was first recalled that the values of u_j and G_j coincided on Γ_R, and pressure p was known in terms of W, leading to

Where

just depending on the variation of u along Γ_R. Operator T(u) represented Dirichlet to Neumann mapping. It was stated that variational formulation (2) was the weak formulation of the problem

Existence and uniqueness of solutions

Bilinear forms and linear functional F: X→ R defined by

and , respectively, were considered. Variational formulation of (2) would then read: Find (u,p) ∈ X x M so that

The proof of existence and uniqueness was based on Brezzi's theorem, since the form A(u,v) + A₀ (u,v) was continuous andcoercive, and operator B satisfied the inf-sup condition (Han and Bao, 1997; Camargo, 2008).

Finite element method

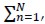The finite element method presented in this article did not approximate the solution of the problem (4), but provided the solution to the problem obtained by truncating operator T(u) in the corresponding Fourier series. If were replaced by for integer value N, the variational formulation of the approximate problem would read: Find ( u_N , p_N ) ∈ X x M so that

with j = 1, 2. The study of existence and uniqueness of the problem (5) was similar to the exact problem (Han and Bao, 1997; Camargo, 2008). Furthermore, the following error estimate of the approximation ( u_N , p_N ) held.

Theorem 1. were the solutions to variational problems (4) and (5), respectively. In addition, it was supposed that with ∈ Z. Then the following abstract error estimate would hold

where C was a constant independent of N and M.

Next, X_h С X and M_h С M were the spaces of finite element corresponding to Taylor-Hood element (Brezzi, 1991). The regular partition of domain Ω_i was denoted by T_h using curved triangular elements T having diameter h_T , where . Then, the finite element method of (5) would read: Find o that

Notice that the Taylor-Hood element satisfied the inf-sup condition (Brezzi, 1991) and again, by Brezzi’s theorem, the unique solvability of the variational formulation (6) was obtained.

Theorem 2. was the solution to problem (4) and was the solution to problem (6), then the following error estimate would hold

where C was a constant independent of h and N.

Proof. Let be the solution of problem (5) for any integer N ≥ 0 and consider errors and then according to the standard technique of mixed finite element method, would exist independently of N and diameter h of triangulation Ω_i so that

Therefore,

and (7) would yield

concluding the theorem proof.

Implementing the DD†N technique

Let Ω be unbounded domain the circumference with radius R = 2 and.

Where and then, would be the unique solution for the following boundary value problem

Given n ∈ N, let a partition uniform of be the parametrisation of a circle defined by y(t)= R(cos (t), sen(t))^T. The annular region bounded by was then denoted by Ω_h and closed polygonal line Γ_h with vertices and T_h was regular triangulation of Ω_h with triangles T of diameter h_T so that .

Reference triangle with vertices was then considered and the family of similar bijective transformations introduced so that for all T ∈ T_h. It is well-known that whe-re and depend on the vertices of triangle T. Therefore, given integer l > 0 and subset S of R² P_i( S) denoted the space of polynomials defined in ?? having two variables and great degrees of freedom at most L.

Next,

was defined to specify X_h and M_h and discretised X and M using

Figure 2. Sequence T_o,h, … T_3,h of meshes used in the implementation

and

Spaces X_h and M_h were Hood and Taylor finite element subspaces satisfying inf-sup condition. Several triangulations were used in our numerical experiment. Numerical experimentation was started with initial mesh T_o,h which had 26 elements. Each uniformly refined mesh T_1,h ,…,T_3,h was generated by dividing each triangle into four smaller triagles.The result can be seean in figure 2.

Table 1. Degrees of freedom and norm L² of errors when N = 7

Table 1 . show norm L² of errors u - u_h,N¸ p - p_{h, N} when N =7 for meshes T_o,h,…,T_3,h

Table 2. Norm L² of errors for T_3,h when N = 0, 1, 3, 5, 7

Table 2 shows norm L² of errors u - u_h,N¸ p - p_{h, N}5 for mesh T_3,h when N = 0, 1, 3, 5, 7.

Figure 3 shows values of and p_h for meshes T_{0, h,} T_{1, h,}, T_{3, h,} and ?N = 7. As Figure 3 shows, N = 7 produced a good approximation and only a few terms were needed in bilinear form A₀ to obtain good results.

Conclusions

D†N mapping was used this paper to approximate the solution of an unbounded exterior problem. An artificial boundary was introduced into the domain to approximate the solution on a bounded computational domain by using a finite element method

.The Taylor-Hood element defined in terms of a Fourier series on the artificial domain was implemented in this work as finite element method. The numerical calculations showed that good convergence had been obtained just by truncating the Fourier series to seven terms. However, our discretisation produced a dense stiffness matrix, corresponding to the boundary operator; special preconditioners have to be used to obtain good convergence by very refined meshes.

Figure 3. and p_h for the meshes T_o,h,…,T_1,h and T_3,h when N = 7.