Introduction
Foundations, referred to as sub-structures, are an integral part of an engineered structural system. They safely transfer and distribute the load from the superstructure to the underlying soil/rock strata, so that neither the soil/rock fails in shear nor the foundation itself. The foundation/sub-structure constitutes an embedded part of the structure and acts as an intermediary between the superstructure and the ground on which the foundations are laid. The bearing capacity and the settlement characteristics of the underlying ground strata significantly govern the design of the foundation system and the structure's serviceability. The shear failure and or excessive settlement of the ground strata results in a distortion of the superstructure. Therefore, great attention must be paid to all the affecting factors.
Numerous studies have been conducted with the aim to predict the response of shallow foundations, and many pioneers (Prandtl, 1920; Terzaghi, 1943; Skempton, 1951; Meyerhof, 1963; Hansen, 1970; Vesic, 1773) have contributed to this theory. Thus, the expressions for estimating the bearing capacity and settlement aspects of shallow foundations resting on the soil and the rock strata have been derived. Notably, this theory and these equations are exceptionally valid for an isolated foundation system where no foundation exists in an isolated state. In several situations, individual or groups of foundations are persistently built in close proximity. Some of these situations include deficient construction space, restrictions in the property line, structural design requirements, and building architecture. Recently, with the increased expansion of infrastructures in conjunction with a rapid urbanization, and in order to tackle the problem of construction space, structures and sub-structures have been forced to come ever close to each other. In a way, foundations have been laid with closer spacing. Under such situations, the bearing capacity, settlement, failure mechanisms, and rotational characteristics are invariably different from those of isolated foundations. This may be due to the influence of one foundation on the other, as they are so closely laid. The stress isobars or the failure zones of neighboring foundations may combine or interfere with each other, leading to the phenomenon known as foundation interference/interaction. The overlapping of individual stress isobars or failure zones combines to form a single stress isobar or failure zone that extends both laterally and vertically, affecting large soil masses. This phenomenon alters the behavior of closely placed foundations when compared to the fundamental behavior of isolated ones, which also includes those that are placed far enough from each other so that may be considered to be isolated.
Many researchers have studied the problem by performing small-scale laboratory or field tests, as well as by conducting theoretical or numerical analyses on an unreinforced soil medium. These studies have implemented different theoretical or numerical techniques, such as a method of stress characteristics (Graham et al., 1984; Kumar and Ghosh, 2007a); upper bound limit analysis (Kumar and Kouzer, 2008; Kouzer and Kumar, 2008, 2010; Kumar and Ghosh, 2007b; Yang et al., 2017; Biswas and Ghosh, 2018; Keawsawasvong et al., 2021; Yodsomjai et al., 2021); lower bound limit analysis (Kumar and Bhattacharya, 2010, 2013; Shiau et al., 2021; Keawsawasvong and Boonchai Ukritchon, 2022); the finite difference method (Ghazavi and Lavasan, 2008; Ghosh and Sharma, 2010; Mabrouki et al., 2010; Lavasan and Ghazavi, 2012b; Javid et al., 2015; Lavasan et al., 2017); the finite element method (Lee et al., 2008; Lee and Eun, 2009; Kumar and Bhoi, 2010; Nainegali et al., 2013, 2018, 2019; Noorzad and Manavirad, 2014; Zidan and Mohamed, 2019; Sekhar et al., 2020; Shokoohi et al., 2019; Fuentes et al., 2019; Ekbote and Nainegali., 2019a, b; Sekhar et al., 2020; Alzabeebee, 2020, 2022; Ekbote et al., 2022); the analytical method (Kumar and Saran, 2003b, 2004; Ghosh et al., 2017); and the probabilistic approach (Griffiths et al., 2006).
In this vein, the ground improvement technique is a potentially cost-effective method, as it provides soil reinforcement for shallow foundations, constituting an alternative to conventional deep foundations wherever applicable. Soil reinforcement is carried out in several layers below the foundations, using geotextile, geogrid, geocell, or geocomposite materials. The use of reinforcement in the soil creates a composite material, increasing the bearing capacity and reducing the settlement of the foundations. Several numerical and experimental studies have been reported with regard to the effects of interference on reinforced soil beds. Moreover, several experimental studies on reinforced soil media have also been performed (Khing et al., 1992; Al-Ashou et al., 1994; Kumar and Saran, 2003a; Ghosh and Kumar, 2009; Lavasan and Ghazavi, 2012a; Naderi and Hataf, 2014; Gupta et al., 2018; Saha Roy and Deb 2018; Dehkordi et al., 2019; Paikaray et al., 2020; Swain and Ghosh, 2015). In this vein, an extensive state of the art review regarding the effect of interference on the behavior of shallow footings was carried out by Ghazavi and Dehkordi (2020).
Most of the studies reported in the literature deal with foundations identical in geometry and loading conditions (symmetrical planning). However, in many situations, structures located close to each other may have different configurations regarding their foundations; the shape of a foundation, as well as its size, may differ, and the super-structural load may be different. This gives rise to asymmetrical interference in the footings.
The subject of interference considering asymmetrical footings is rarely mentioned in the literature. Nainegali et al. (2013) highlighted the settlement of asymmetrical interfering strip footings laid on the surface of a linearly elastic non-homogeneous soil medium of finite and semi-infinite extent. Furthermore, they extended the study (Nainegali et al., 2018) to examine the interference effect on the bearing capacity and settlement of asymmetrical strip footings on the surface of a non-linearly elastic dense and loose sandy soil medium. In both studies, asymmetry affects the size of the footings, and the surcharge effect is not considered. Ghosh et al. (2017) examined the interference of two closely spaced asymmetric footings using the Pasternak model. They considered the hyperbolic stress-strain relation and performed linear and nonlinear elastic analyses. Ekbote and Nainegali (2021) studied two closely spaced asymmetric footings while considering different widths embedded in a homogenous, isotropic soil medium. The study focused on the effect of the width and embedment depth of the two footings, and its results align with earlier reports in conjunction with asymmetry. However, the embedment depth of the footings was also found to have a significant effect.
Most studies have been performed on surface footings, but, from a practical point of view, it is not viable to lay the foundation on the ground level (surface). Therefore, the reported literature does not give a clear picture of the interference effect on embedded footings.
For most structures, the foundations are laid below the ground surface (i.e., embedded in nature). The overburden/ surcharge from embedment amplifies the bearing capacity and reduces the settlement since there is an enhanced shearing zone. The literature on the effect of interference when footings are in a state of embedment in the reinforced soil medium is virtually null, and there is no study on the subject for embedded shallow footings. Therefore, this phenomenon must be analyzed. Moreover, bearing capacity and settlement are the primary criteria for shallow footing design, so, in order to overcome inadequacies and fill the research gap, this study focuses on these aspects of embedded shallow foundations resting on a reinforced soil medium while considering the embedment depth (same level).
Stating the problem
Figure 1 represents the problem domain, discretized using a structured finite element mesh and associated with appropriate boundary conditions. The problem considers two asymmetrical interfering strip footings with widths of BL (left footing) and BR (right footing), embedded at a depth Df below the ground level, and laid with a clear spacing S. The footings are rigid, rough, and subjected to a load intensity q per-unit length of uniform load intensity. The foundation soil medium is assumed to be a homogeneous, isotropic, and semi-infinite cohesionless medium reinforced with a single and a double layer of geosynthetic material. The first layer (N = 1) of reinforcement is laid at a depth u below the base of the footings, and the consecutive layer (N = 2) at a depth h from the first reinforcement layer. The objective of this research is to perform a parametric study, varying contributing parameters such as the embedment depth of the footings (Df), the width of the right footing (BR), the soil friction angle (ф), the number of reinforcement layers, and the spacing between the footings (S). This works aims to explore the influence of the interference phenomenon on the behavior of asymmetrical footings (i.e., ultimate bearing capacity, settlement, load-settlement response, and displacement pattern). Note that the right footing width is varied while the left footing width is kept constant. The range of varied parameters is shown in Table 1.
Methodology
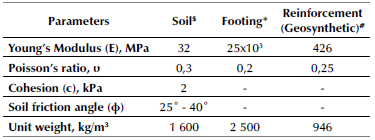
The numerical analysis of the problem defined in the previous section employs the finite element method via the commercially available ABAQUS V6.13 software. The studied problem is regarded as a plane strain one since the footing length relative to the width is much higher. The interfering footings are considered asymmetrical with respect to the width of the footings, which are embedded at the same depth and loaded with the same magnitude. The width of the left footing is kept constant, and the width of the right interfering footing BR is varied (Table 1). The Mohr-Coulomb failure criterion is used given its practical significance. It offers the best numerical approximation within the broad confining pressure range, as well as a trustworthy outcome for various nonlinear studies of the ground. Moreover, this criterion is used due to its mathematical simplicity and clear physical significance of the material parameters (Erickson and Drescher, 2002; Labuz and Zang, 2012). Accordingly, the soil medium is modeled as a linearly elastic, perfectly plastic material in compliance with the aforementioned criterion (Ghazavi and Lavasan, 2008; Mabrouki et al., 2010; Shokoohi et al., 2018; Zidan and Mohamed, 2019; Sekhar et al., 2020). The footings embedded at the required depth are defined as a rigid and rough, linear elastic material (Vivek, 2011; Noorzad and Manavirad, 2014). The thickness of the footings equals their embedment depth. The reinforcement (geosynthetic) material behaves axially and as a linearly elastic material (Basudhar et al., 2007; Nazzal et al., 2010). The mechanical properties considered for the soil, the footings, and the reinforcement are specified in Table 2.
The foundation soil domain is discretized with structured meshing using two-dimensional plane strain linear continuum elements (CPE4R). A structured discretization meshing scheme is applied, which involves adopting fine mesh in the vicinity of high-stress concentration (around the interfering footings), as well as subsequent coarser meshing in the region of low-stress concentration, such as far-end boundaries. The dimensions are set after a sensitivity analysis regarding domain and mesh size and considering the accuracy of the results. The domain size considered in the analysis is presented in Figure 1. For the element size, elements with a uniform mesh of size 0,2 m are considered within a domain up to five times the width of the footing (5BL) on either side (horizontal direction) and five times the width of the footing (5BL) from the base (vertical direction). Thereupon, the elements vary from 0,2 to 0,8 m at the far-end boundaries using the single bias technique of the ABAQUS meshing module. A detailed mesh convergence study and a domain sensitivity analysis are presented in the recent article published by Ekbote and Nainegali (2021).
Table 2 Mechanical properties of the soil, footings, and reinforcement considered in the analysis
Source: $Mabrouki et al. (2010); *Vivek (2011); #Nazzal et al. (2010)
The geosynthetic reinforcement material is modeled as linearly elastic and discretized using two-dimensional quadratic truss elements (T2D3) that resist axial forces and do not resist any bending action. The reinforcement configuration is provided by optimizing the bearing capacity in order to obtain the maximum value. This is also done in Ekbote and Nainegali (2019a). Thus, the depth of the first layer of reinforcement u is 0,35 times BL from the bottom of the footing, the distance between the first and the second layer h is 0,4 times BL, and the length of reinforcement layer b is 5,0 times BL. The interface between the soil and the footing, as well as between the soil and the reinforcement, is modeled using the interaction feature of ABAQUS (surface-to-surface, master-slave contact). Using this feature, there is a master and a slave surface. Defining such surfaces automatically generates a group of contact elements. The interaction simulation consists of normal-to-the-surface and tangential-to-the-surface components. The interface in the normal direction is assumed as hard contact with no separation allowed between the surfaces. The shear interactions are defined using Coulomb's friction law, by virtue of which a tangential behavior is defined between the contact surfaces a coefficient of friction ц, which is equal to the tangent of soil friction angle ф (ц = tan ф). Appropriate boundary conditions essential for the solution approximation are established along the horizontal and vertical boundaries of the foundation soil domain. The suitable boundary conditions at the extreme boundaries are assigned in line with Potts and Zdravkovic (1999). Roller supports are considered along the far-end boundaries AD and BC in order to restrict the horizontal displacement (u1 = 0) and allow any possible vertical displacement (u2) at the far ends. Otherwise, the boundary DC is fixed to restrict horizontal and vertical displacements (u1 = u2 = 0).
Validation
This model was validated with the results of Nainegali et al. (2013, 2018). Nainegali et al. (2018) conducted a finite element analysis to study the settlement behavior of adjacent footings while considering the conditions of symmetry and asymmetry with respect to footing size and the applied loading with different combinations. Rough, rigid strip footings were placed on the surface of either a linearly elastic finite or an infinite non-homogeneous soil bed. Nainegali et al. (2013) presented their results in terms of the interference factor, which is the ratio of the average settlement of left/right footing in the presence of the right/left footing to that of the settlement of isolated footings. Nainegali et al. (2018) also performed a finite element analysis of two closely spaced strip footings on the surface of dense, loose, cohesionless soil beds. The footings were considered either symmetrical or asymmetrical based on their size. The soil was modeled following the non-linearly elastic soil, obeying the Duncan and Chang hyperbolic constitutive relationship. The results were presented in terms of interference factors such as the ratio of bearing pressure/settlement of interfering footings to that of isolated footings.
Table 3 Mechanical properties of soil considered for validation

Source: Nainegali et al. (2013, 2018)
The adopted model was validated by adopting the soil properties presented in Table 3 (Nainegali et al., 2013, 2018). The results of the comparison are presented in Figures 2a and 2b regarding Nainegali et al. (2013) and Nainegali et al. (2018), respectively. The variation was found to be similar and almost matching. However, a slight difference was observed in our results, given the difference in the discretization scheme and the size of the elements considered. The differences in the computed interference factor at S/BL = 0,50 for the left and right footings when compared to that of Nainegali et al. (2013) are 5 and 1%, respectively. Similarly, these differences, in comparison with Nainegali et al. (2018), are 1,5% and 1,9%, respectively. Overall, it can be seen that this finite element analysis model can be used reliably to address the aforementioned problem.
Results
A rigorous finite element analysis was performed to investigate the effect of interference on closely placed footings while considering asymmetry with respect to dimension (width), emphasizing the embedment of the footings in a geosynthetic reinforced soil medium. The analysis results regarding non-dimensional interference factors associated with the ultimate bearing capacity and the settlement were interpreted. The interference factor for the ultimate bearing capacity was estimated as defined in Equations (1a) and (1b) for the left and right footings, respectively. Similarly, the interference factor for the settlement was estimated according to the definitions given in Equations (2a) and (2b), for the left and right footings.
The permissible settlement (δP) is the maximum settlement allowed, irrespective of the footing type and size. As per the Indian Standard Code (IS 1904-1986), the maximum permissible settlement is 50 mm for isolated foundations in sand and hard clay for steel and reinforced concrete structures. The permissible bearing pressure (qP) is the pressure corresponding to the δP assumed for an isolated footing. qP (which corresponds to δP = 50mm) for different footing widths, depth of embedment, and soil friction angles was estimated, in the case of an unreinforced soil medium, by Ekbote and Nainegali (2021) (Table 4). These values are used to evaluate the interference factor for the settlement, as defined in Equations (2a) and (2b).
Table 4 Permissible bearing pressure qP corresponding to the permissible settlement 5P for an isolated footing

Source: Ekbote and Nainegali (2021)
Source: Authors
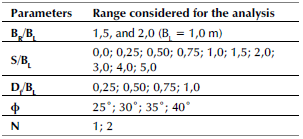
Figure 3 p-δ plots for interfering asymmetric footings embedded in reinforced soil. D/BL = 1,0, ф = 30°, BR = 2,0BL, N = 2.

Source: Authors
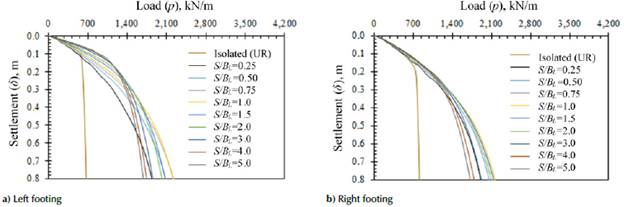
Figure 4. Variation of ξ r L and R ξ r R with the S/BL ratio for various Df/BL values in soil with ϕ = 30°: BR = 1,5BL
The load-settlement (p-δ) response of the left and right asymmetrical interfering footings placed at different spacings (S/BL ratio) for the case of BR = 2,0BL, embedded at depth, and D/BL=1,0 in soil a having friction angle of ф=30° and reinforced with a single layer (N = 2) of reinforcement are illustrated in Figures 3a and 3b. The p-δ curve of the corresponding identical isolated footing embedded in an unreinforced soil bed (Isolated (UR)) is also shown in the figures for comparison. It can be noted that the response of asymmetrical interfering footings differs when compared to that of isolated ones. An explanation for the increased bearing capacity with a decreased footing spacing can be found in Stuart (1962). The load-carrying capacity increases with an increase in the number of reinforcement layers. The enhanced shear strength of the reinforced soil bed, which also increases with the number of reinforcing layers, is responsible for the higher load bearing capacity. According to Shukla (2021), the friction between the soil and the reinforcement layers primarily drives the reinforced soil's composite system. Additionally, the presence of or increase in reinforcement layers transforms the mechanism of soil shear failure into one of general shear failure (Guido et al., 1985). From Figure 3, it can be stated that the p-δ curves of the interfering footings for spacings greater than 3,0 are more or less overlapping. This indicates that the interfering footings are starting to act as an isolated one. It cannot be ignored that there is a significant effect due to the asymmetry of the base (width of the adjacent base), i.e., there is a behavioral difference in p-δ for both the left and the right footings. For the smaller left footing, the p-δ curves for different spacings are more distributed than those of the larger right footing.
By obtaining the bearing capacity from the load-settlement curves, the interference factors associated with the ultimate bearing capacity for the left footing (ξ r L ) and the right footing (ξ r R ) were evaluated for the range of parameters varied in the analysis, using Equations (1a) and (1b), respectively. The load-settlement curves obtained for the interfering footings do not show a definitive failure point. Therefore, in order to obtain the ultimate bearing capacity, a double-tangent method was used, referring to Naderi and Hataf (2014), Ghosh et al. 2015), and Saha Roy and Deb (2018). The variations in ξ r L and with spacing (S/BL ratio) for footing embedment at different depths (Df/BL ratio) in soil having a friction angle of ф = 30° for the case of BR = 1,5BL are presented in Figures 4a and 4b for single (N = 1) and double (N = 2) layers of reinforcement. The case of BR = 2,0BL is illustrated in Figures 5a and 5b. Similarly, Figures 6a and 6b, for N = 1 and 2, present these variations for the case of BR = 1,5BL, footings embedded at D/BL = 1,0, and different soil friction angles. The same is illustrated in Figures 7a and 7b for the case of BR = 2,0BL.

Source: Authors
Figure 5 Variation of ξ r L and ξ r L with the S/BL ratio for various Df/BL values in soil with ϕ = 30°: BR = 2,0BL
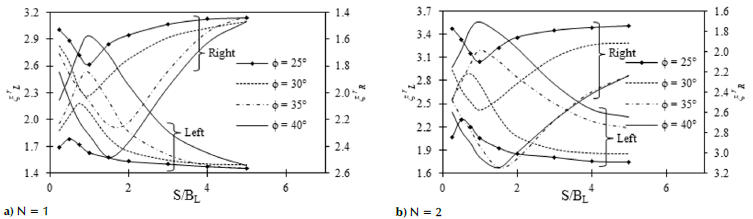
It can be observed, in Figures 4a, 4b, 5a, and 5b, that the footings embedded at smaller depths have higher interference factors. The interference factors of each footing are presented on either side of the figures. The peak interference factors ( g L and Ç R ) decrease progressively with an increased embedment depth of the footings. Moreover, the peak interference factors increase with the soil friction angle. The spread of the plastic zone beneath the footing grows with an increase in soil friction angle, which is often related to an increasing shear strength. Additionally, when the soil friction angle increases, the failure pattern expands in the lateral and downward directions with increasing scope (Kouzer and Kumar, 2010; Yang et al., 2017). Furthermore, Figures 6a, 6b, 7a, and 7b show that the spacings at which the peak occurs increase for the right footing when compared to the left footing.

Source: Authors
Figure 6 Variation of ξ r L and ξ r R with the S/BL ratio for various soil friction angles at D/BL = 1,0: BR = 1,5BL
Source: Authors
Figure 7 Variation of r ξ r L and ξ r L with the S/BL ratio for various soil friction angles at Df/BL = 1,0: BR = 2,0BL
In Figures 4-7, knowing the interference factor, the percent increase in the bearing capacity of the interfering footings can be obtained in comparison with the corresponding isolated footing, i.e., [( ξ r L or-ξ r 1,0) x 100]. As an example, it can be noted that, for D/BL = 1,0 for the left footing when BR = 2,0BL, placed with one layer of reinforcement (N = 1) and ф = 25°, 30°, 35°, and 40° the percent increase in the bearing capacity of the interfering footings at S/BL = 0,50 is 78, 104, 118, and 148%, respectively, compared to their corresponding isolated footing. In the case of a specified angle of soil friction and spacing ratio, according to Equation (1), the interference factor increases with a decrease in the depth of the footing embedment. However, the load-carrying capacity of the soil increases with an increase in the embedment depth of the footing, due to an increased shearing zone and enhanced overburdening. The bearing capacity predominantly increases with an increase in the embedment depth for both isolated and interfering footings. As an example, consider a specified ф = 30° and S/BL = 0,5 for the case BR = 2,0BL. The bearing capacity of the left footing when N = 1 increases from 104 to 185%, with a decrease in the depth of footing embedment from Df/BL = 1,0 to 0,25. The improvement in the ultimate bearing capacity for symmetrical interfering footings in a soil medium reinforced with N-layers of geosynthetic material is evident in earlier research on surface footings (Ghazavi and Lavasan, 2008; Lavasan et al., 2017; Biswas and Ghosh, 2018) and embedded footings (Ekbote and Nainegali, 2019a), which holds true in the case of asymmetric footings. However, ξ L r,mrx is higher than ξ R r,mrx . The peak interference factors for ф = 2 are shown in Table 5 for various embedment depths, soil friction angles, and footing widths. For the footings embedded at D/BL = 1,0, the percentage difference in ξ L r,mrx and ξ R r,mrx for ф = 25°, 30°, 35° and 40° for BR = 1,5BL is 8,6, 12,3, 7,7, and 8,6%, respectively. Similarly, for BR = 2,0BL, these values are 8,3, 10,7, 1,6, and 11,5%, respectively. The percentage decrease in ξ L r,mrx for N = 2, BR = 2,0BL when the embedment depth is increased from 0,25 to 1,0 for ф = 25°, 30°, 35° and 40° is 43,23, 39,44, 53,75, and 42,41%, respectively, and the percentage decrease in ξ R r,mrx for ф = 25°, 30°, 35°, and 40° is 73, 52, 40, and 42%.
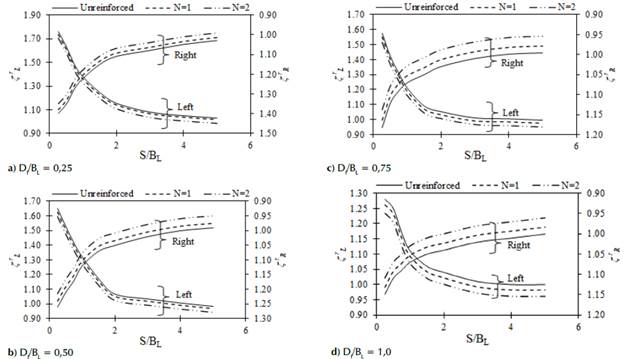
The settlement analysis of asymmetrical interfering footings embedded in a reinforced soil medium was carried out by evaluating the settlement at the bearing pressure corresponding to the permissible settlement of an isolated footing (50 mm) embedded in an unreinforced soil medium. The permissible bearing pressures corresponding to the permissible settlement for given values regarding the right footing width, embedment depth, and soil friction angle is shown in Table 4. Accordingly, the interference factors for the settlement of the left footing (ξ L r ) are calculated using Equation (2a) and those for the right footing (ξ R r ) using Equation (2b). The variations of ÇR and ξ R r with spacings for N = 1 and 2 and the unreinforced case (N = 0) are presented in Figures 8a, 8b, 8c, and 8d for footings embedded at depths Df/BL = 0,25, 0,50, 0,75, and 1,0, respectively, with BR = 1,5BL and ф = 30°. The magnitude of the settlement interference factors of the left footings (ξ L r ) are presente d on the left-hand side of the figures, and those of the right footings (ξ R r ) are presented on the right-hand side with values in reverse order. The width of the right footing (BR = 2,0BL) is shown in Figures 9a to d. Similarly, the variations of ξ L r and ξ R r with spacings for different soil friction angles (ф = 25°, 30°, 35°, and 40°) and D/BL = 1,0 when BR = 1,5BL and BR = 2,0BL are presented in Figures 10a to d and 11a to d. The settlement interference factor continuously decreases with increased spacing between the footings for all the soil friction angles and embedding depths considered as the arching. The confinement effect of soil diminishes with the increasing proximity of the footings. The maximum settlement (ξ L r,max and ξ R r,max ) occurs at the minimum spacing considered (S/BL = 0,25). However, the magnitude of the settlement decreases with an increase in both the embedment depth and the friction angle. The settlement was found to decrease further with the introduction of reinforcement layers, which is due to an increase in the shear strength of the soil.
The percentage decrease for the maximum settlement, given a footing width BR = 1,5BL, with N = 1 and ф = 30°, when the footing embedment depth is increased from D/BL = 0,25 to 1,0, is 21% for the left footing and 20,7% for the right one. Similarly, the percentage decrease in the maximum settlement when the embedment depth is increased from D/ BL = 0,25 to 1,0 for BR = 2,0BL, N = 1, and ф = 30° is 22,3% for the left footing and 20,9% for the right one. Furthermore, the decreases in the settlement when the soil friction angle is increased from ф = 25° to 40° L 1,0, BR = 1,5BL, and N = 1, for the left and right footings, respectively. These values (when BR = 2,0BL) are 14% for the left footing and 7,2% for the right one. Similarly, the decrease in the settlement when the soil friction angle is increased from ф = 25° to 40° for Df/BL = 1,0, BR = 1,5BL, and N = 2 is 11,1% (left footing) and 5,8% (right footing). For BR = 2,0BL, these values are 13,9 and 7,2%, respectively.

Source: Authors
Figure 8 Variations in ξ r L and ξ r R with S/BL ratio for N = 0 (unreinforced), 1, and 2 at different embedment depths in soil with ф = 30°: BR = 1,5BL
Source: Authors
Figure 9 Variations in ξ r L and ξ r R with S/BL ratio for N = 0 (unreinforced), 1, and 2 at different embedment depths in soil with ф = 30°: BR = 2,0BL

Source: Authors
Figure 10 Variations in ξ r L and ξ r R with the S/BL ratio for N = 0 (unreinforced), 1, and 2 in soil with different ф, with D/BL = 1,0: BR = 1,5BL
Table 5 Peak interference factors (ξ L r,max max and ξ r R max ) for different D/BL, ф, and BR/BL values for two layers of reinforcement

Source: Authors

Source: Authors
Figure 11 Variations in ξ r L and ξ r R with the S/BL ratio for N = 0 (unreinforced), 1, and 2 in soil with different ф and D/BL = 1,0: BR = 2,0BL
The failure of the two closely placed asymmetrical footings can be visualized through the total displacement contour plots and is presented for BR = 2,0BL and Df/BL = 1,0 in a soil medium (ф = 30°) with a double layer of geosynthetic reinforcement (Figures 12a, 12b, 12c, and 12d) for footings spaced at S/BL = 0,25, 0,50, 1,0, and 5,0. The plots correspond to the ultimate bearing capacity. The displacement vectors are also shown over the plots to represent the direction and magnitude. Figures 12a to d show a general form of shear failure. It can be observed (Figures 12a and 2b) that the displacement vectors in between the two footings are absent, i.e., the soil heave is not observed. This implies that adjacent footings with very close spacings (S/BL = 0,25 and 0,50) act as one unit and relate to the single footing having a greater width (BL+S/BL+BR). Furthermore, with an increase in spacing (Figure 12c), the heave between the footings is observed. However, this coincides with the passive zones of the close footings, and, at far away spacings (Figure 12d), the footings start behaving as independent ones. When the soil medium is reinforced, the zone between the two footings gets more confined than in unreinforced soil. Thus, the soil starts to densify until the shear failure occurs. The load carrying capacity was found to increase with a decrease in the settlement. The failure in the reinforced soil medium was assumed to be related to shear given a slip between the soil and the reinforcement (Basudhar et al., 2008).
Conclusions
The performance of two closely spaced asymmetric footings embedded in a cohesionless reinforced foundation soil medium was studied using finite element analysis. Asymmetry was considered only with respect to the width of the footings, and thus the entire domain was used in the analysis while adopting appropriate boundary conditions. A sensitivity analysis for the domain and element size was performed, and the finite element model was validated with benchmark problems reported in the literature. The influence of the interference phenomenon on the load-settlement response, the ultimate bearing capacity, the settlement, and the displacement pattern was analyzed by varying several contributing parameters. Observations on the ultimate bearing capacity and the settlement were presented in terms of non-dimensional interference factors defined for this purpose. This study leads to the following conclusions:
The effect of the interference phenomenon is significant, and its influence is asymmetry, that is, the influence of the large footing on the small adjacent one is predominant.
The depth of footing embedment and the soil friction angle have a noteworthy influence on the interference effect.
For a given depth of embedment, the peak interference factor associated with the ultimate bearing capacity increases with an increase in the soil friction angle. It also decreases with an increase in the embedment depth of the footing for a given value of soil friction angle.
The interference factors associated with the ultimate bearing capacity for the reinforced soil medium ( L r and ) vary similarly to those of unreinforced soil with spacing between the footings.
In comparison with the unreinforced soil medium, the settlement analysis for the reinforced soil medium (which considered the corresponding permissible limit) was found to follow a similar variation regarding the interference factors (Ç r L and Ç R ) and the spacing between the footings. However, the magnitudes were found to decrease, which accounts for the reduced settlement. Reductions in the settlement magnitude of 1,5 and 4,5% were noted for N = 1 and N = 2, respectively.