Grupo INSIGHT. Bogotá, DC., Colombia.

Correspondencia: Javier Rodríguez, MD. Grupo INSIGHT. Dg 51A Bis No. 56C-25 Sur. Bogotá, DC., Colombia. Teléfono: 2382108. Correo electrónico: grupoinsight2025@yahoo.es

Recibido: 16/12/05. Aprobado: 12/11/06.

La teoría fractal permite la caracterización objetiva de objetos irregulares. La ramificación coronaria izquierda es un objeto irregular que en la actualidad se evalúa por medio de la arteriografía, donde se determina la enfermedad arterial oclusiva a partir de la comparación de medidas entre segmentos arteriales, sin evaluar el impacto de la lesión en la ramificación coronaria total. La irregularidad de la totalidad de la ramificación coronaria puede evaluarse con dimensiones fractales.

De manera fractal se caracterizaron imágenes consecutivas entre sístole y diástole de nueve pacientes con enfermedad arterial oclusiva moderada y se confrontaron con las medidas de siete pacientes con enfermedad arterial oclusiva severa y siete sin enfermedad arterial oclusiva mediante comparaciones de la variabilidad y la diferencia neta. Los pacientes con lesión moderada y sin enfermedad arterial oclusiva, presentan un comportamiento matemático que se caracteriza por mayor variabilidad, mientras que los pacientes con enfermedad arterial oclusiva severa presentan diferencias netas generalmente iguales a 0.

Palabras clave: enfermedad arterial oclusiva, dimensión fractal, ramificación coronaria izquierda, angiografía.

The fractal theory allows the objective characterization of irregular objects. The left coronary artery ramification is an irregular object actually evaluated by means of arteriography, in which the occlusive arterial disease is evaluated through the comparison of measures between arterial segments, without evaluating the impact of the lesion in the whole coronary ramification. The irregularity of the whole coronary ramification can be evaluated through fractal dimensions.

Consecutive images between systole and diastole of nine patients with moderate occlusive arterial disease were characterized in a fractal way and were confronted with the measures of seven patients with severe occlusive arterial disease and with seven without occlusive arterial disease by comparing the variability and the net difference. Patients with moderate lesion and without occlusive arterial disease have a mathematical behavior characterized by a greater variability, while patients with severe occlusive disease have net differences generally equal to 0.

Key words: occlusive arterial disease, fractal dimension, left coronary ramification, left coronary artery, angiography.

Introducción

La geometría fractal es una teoría matemática con la que se evalúa la irregularidad de objetos de la naturaleza, permitiendo su medición objetiva (1). Esta teoría surgió al estudiar los problemas de la utilización de geometría euclidiana a objetos irregulares, donde se demostró que su aplicación conducía a resultados paradójicos y carentes de sentido (2). Su aplicación en fenómenos tan diversos como la aparición y distribución de las ramificaciones de los ríos en hidrología o la irregularidad de los índices económicos de las bolsas de valores, ha arrojado resultados objetivos y eficaces en diferentes disciplinas (3-5).

El uso de dimensiones fractales ha sido de gran importancia en el campo clínico y experimental en medicina, al permitir la caracterización de objetos como la estructura neuronal y pulmonar, los intestinos y la irregularidad de las ramificaciones vasculares, entre otros (6). Esta perspectiva ha permitido consolidar nuevas metodologías de diferenciación entre salud y enfermedad tanto a nivel morfológico como fisiológico (6-17). Ejemplo de ello son los trabajos de Pohlman y colaboradores (7) y Lefebvre y Benali (8), quienes caracterizaron imágenes mamográficas con lesiones neoplásicas y sin ellas mediante dimensiones fractales, contribuyendo en el desarrollo de metodologías para la disminución de falsos positivos. Sin embargo, la observación de dimensiones fractales aisladas, puede ser insuficiente para establecer evaluaciones de aplicación experimental efectiva.

Rodríguez y colaboradores (9) evaluaron el proceso de reestenosis en un modelo de experimentación con arterias de porcinos, desarrollando el concepto de armonía matemática intrínseca, el cual permite relacionar matemáticamente dimensiones fractales de las partes con la totalidad de la arteria, diferenciando matemáticamente salud de enfermedad. A nivel fisiológico, Huikuri y colaboradores (10) realizaron una caracterización de la dinámica cardiaca aplicando geometría fractal en pacientes con infarto agudo del miocardio, con una fracción de eyección menor al 35% superando los factores predictores de muerte convencionales.

La aterosclerosis coronaria estenosante avanzada, se asocia con el 90% de los casos de cardiopatía isquémica, patología que produce el 80% de las muertes de origen cardiaco (18). Uno de los métodos para su detección es la angiografía, cuya evaluación se realiza mediante una comparación entre mediciones euclidianas del sector estenosado y un segmento sano, lo que no tiene en cuenta la irregularidad propia de la ramificación coronaria izquierda y no se obtiene una evaluación del impacto de la lesión en la totalidad de la misma ramificación en movimiento; además la interpretación de las mediciones utilizadas depende de la subjetividad del observador.

De acuerdo con estas observaciones, Rodríguez y colaboradores (19) desarrollaron una metodología original de caracterización matemática objetiva de la ramificación coronaria izquierda a partir de dimensiones fractales de las imágenes consecutivas entre sístole y diástole, medidas con el método de Box-Counting y evaluadas con los conceptos de variabilidad y diferencia neta. Los investigadores hallaron que generalmente los pacientes sin enfermedad arterial oclusiva y enfermedad arterial oclusiva moderada, presentan mayor variabilidad en comparación con los pacientes con enfermedad arterial oclusiva severa, caracterizada en general por diferencias netas diferentes de cero, evaluando la dinámica fractal de la ramificación en movimiento.

El objetivo de nuestra investigación es aplicar la geometría fractal para caracterizar de manera objetiva la enfermedad arterial oclusiva moderada y realizar comparaciones con los resultados ya obtenidos en pacientes con enfermedad arterial oclusiva severa y ausencia de enfermedad arterial oclusiva. Esto constituye un paso fundamental en la futura construcción de una generalización de esta metodología para el establecimiento de diferencias entre salud y enfermedad, así como la evolución entre ambos estados a nivel de diagnóstico clínico.

Material y métodos

Población a estudio

Se seleccionaron nueve pacientes del Departamento de Hemodinamia de la Fundación Cardioinfantil, con diagnóstico de enfermedad arterial oclusiva moderada de acuerdo con la evaluación angiográfica tradicional realizada por especialistas de la Fundación.

Justificación

El método actual de evaluación de la enfermedad arterial oclusiva, no aplica medidas apropiadas a la irregularidad del objeto ni tiene en cuenta la estructura total de la ramificación o los cambios morfológicos de ésta en su paso de sístole a diástole, ignorando de este modo el impacto de la lesión en el funcionamiento global. La aplicación de la geometría fractal a la ramificación coronaria izquierda desarrollada por Rodríguez y colaboradores (19), permite no sólo caracterizar de forma objetiva los cambios morfológicos de la ramificación en su paso de sístole a diástole, sino además establecer diferencias entre pacientes sin enfermedad arterial oclusiva y con enfermedad arterial oclusiva severa. Su aplicación a pacientes con enfermedad arterial oclusiva moderada y su comparación con los grupos ya evaluados, constituye un paso importante en la generalización de esta metodología como procedimiento de diagnóstico clínico de la angiografía.

Hipótesis

Los conceptos de variabilidad y diferencia neta, permitirán caracterizar de manera objetiva la ramificación coronaria izquierda de pacientes diagnosticados con enfermedad arterial oclusiva moderada y establecer posibles diferencias o similitudes con pacientes sin enfermedad arterial oclusiva y con enfermedad arterial oclusiva severa.

Objetivos

- Calcular matemáticamente la variabilidad y diferencia neta de las dimensiones fractales de imágenes consecutivas entre sístole y diástole, de la ramificación coronaria izquierda en movimiento en los pacientes evaluados.

- Establecer una metodología de caracterización matemática objetiva apropiada a la ramificación coronaria izquierda con enfermedad arterial oclusiva moderada, aplicando los conceptos de variabilidad y diferencia neta de la dimensión fractal.

- Establecer posibles similitudes o diferencias matemáticas entre pacientes sin enfermedad arterial oclusiva, con enfermedad arterial oclusiva moderada y con enfermedad arterial oclusiva severa.

Metodología

Las angiografías coronarias evaluadas se tomaron mediante la canulación selectiva del ostium de las arterias coronarias izquierda y derecha, para lo cual se requirió una canalización de la arteria femoral por vía percutánea y se insertaron catéteres intravasculares especiales. Para la visualización de las ramificaciones se utilizó un reproductor de imágenes angiográficas ACOM T.O.P. marca Siemmens.

Las angiografías coronarias de los nueve pacientes elegidos se evaluaron mediante el cálculo de la dimensión fractal de cada una de las imágenes consecutivas constituyentes del examen, mediante el método de Box-Counting (20), tal como lo aplicaron Rodríguez y colaboradores (19). Posteriormente, se evaluó la variabilidad de las dimensiones consecutivas de cada angiografía y se obtuvo el valor de diferencia neta para cada paciente. Estos resultados se compararon con los que se obtuvieron en la investigación previa para grupos de pacientes con lesión severa y sin ella. Para la elaboración de los análisis comparativos los grupos se denominaron del siguiente modo: grupo 1: pacientes sin enfermedad arterial oclusiva, grupo 2: pacientes con enfermedad arterial oclusiva moderada, y grupo 3: pacientes con enfermedad arterial oclusiva severa.

Análisis matemático de las medidas

La evaluación de los cambios morfológicos durante la dinámica cardiaca de la estructura geométrica de la ramificación coronaria izquierda, se realizó a partir de los conceptos de variabilidad y diferencia neta desarrollados previamente (19) aplicados a las dimensiones fractales de las imágenes consecutivas, lo que permitió evaluar el impacto global de la lesión en la ramificación. Para el cálculo de la diferencia neta se consideran los cambios de dos y tres décimas entre dimensiones fractales; la comparación entre los valores de diferencias netas entre los grupos, permitirá establecer las diferencias o similitudes matemáticas entre ellos. Por el carácter matemático de los conceptos utilizados, la caracterización realizada es una medición objetiva y reproducible de cada caso particular, independientemente de las metodologías estadísticas.

Definiciones

Fractal: interrumpido, irregular. Término que se define como sustantivo para objeto irregular y como adjetivo para irregularidad.

Dimensión fractal: medida numérica adimensional del grado de irregularidad de un objeto fractal. La definición de dimensión fractal usada fue la dimensión fractal de Box-Counting.

Dimensión fractal de Box-Counting: generalmente se utiliza para medir fractales salvajes y se define mediante la siguiente fórmula:

N: número de cuadros que contiene el contorno del objeto.
K: grado de partición de la cuadrícula.
D: dimensión fractal.

Variabilidad de la dimensión fractal (19)¹: definición original del primer autor: variaciones en la primera cifra posterior a la coma en medidas consecutivas de la dimensión fractal en la totalidad de la secuencia.

Diferencia neta (19)²: la diferencia neta en una secuencia es la diferencia entre el cambio total creciente y el decreciente. Para calcular el cambio total creciente se suma el doble de las veces que se presenta una variación creciente de dos décimas y el triple de las veces que se presenta una variación creciente de tres décimas en la dimensión fractal, en imágenes consecutivas. De manera análoga se calcula el cambio total decreciente.

Angiografía coronaria: visualización radiográfica de los vasos coronarios después de la inyección de un medio de contraste radio-opaco. Para un diagnóstico preciso se requieren proyecciones coronarias en múltiples vistas: oblicua anterior izquierda, oblicua anterior derecha, con inclinación craneal y caudal, de acuerdo con las características del paciente (21).

Diagnóstico clínico: en la práctica clínica, la manera más común de identificar el grado de lesión estenótica, es mediante la estimación visual en por lo menos dos proyecciones ortogonales; los vasos se valoran por la extensión de la distribución de regularidades luminares, patrón de flujo, lavado de contraste, calcificación y viabilidad de la cirugía de revascularización o la angioplastia. Con base en esto la enfermedad arterial oclusiva se clasifica en leve, moderada y severa (22).

- Leve: cuando la obstrucción es menor o igual a 50%.
- Moderada: cuando la obstrucción es mayor a 50% y menor o igual a 75%.
- Severa: cuando la obstrucción es mayor a 75%.

Resultados

Las dimensiones fractales obtenidas en los diferentes grupos varían entre 1,15 y 1,93; para el grupo 1 estos valores se encuentran entre 1,31 y 1,84; para el grupo 2 entre 1,33 y 1,93 mientras que para el grupo 3 están entre 1,15 y 1,82, tal como se muestra en las tablas 1, 2 y 3. Los valores de variabilidad y diferencia neta oscilan entre 0 y 5 para todos los grupos.

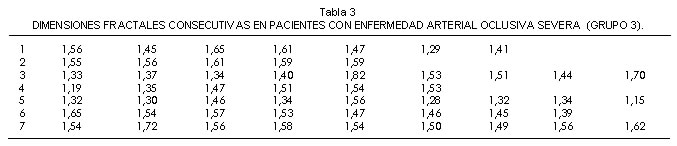
Los grupos de pacientes sin enfermedad arterial oclusiva y con enfermedad arterial oclusiva moderada, presentan un comportamiento matemático semejante, que se caracteriza por una mayor variabilidad evaluada con la diferencia neta, diferenciándose del grupo de pacientes con enfermedad arterial oclusiva severa. Esto se evidencia en que los pacientes del grupo 3 presentaron cinco diferencias netas iguales a 0, mientras que las diferencias netas fueron diferentes de 0 en seis ocasiones tanto para el grupo 1 como para el 2.

Para los grupos 1 y 2 se presentan diferencias netas iguales a 0 sólo una y tres veces respectivamente en cada grupo. Únicamente se presentaron dos diferencias netas de 1 correspondientes a pacientes de los grupos con ausencia de enfermedad arterial oclusiva y enfermedad arterial oclusiva moderada, una de tres en el grupo con enfermedad arterial oclusiva severa y una de cinco en el grupo de pacientes con ausencia de enfermedad arterial oclusiva; no se presentó ninguna diferencia neta de 4. Las diferencias netas de 2 son las más predominantes en los grupos 1 y 2, encontrándose en cuatro y cinco ocasiones respectivamente, mientras que en el grupo 3 sólo aparecen en una ocasión.

Discusión

Este es el primer trabajo en el que se caracterizan matemáticamente los cambios geométricos de la ramificación coronaria izquierda en movimiento, entre sístole y diástole, en pacientes con enfermedad arterial oclusiva moderada, y se comparan los resultados con medidas análogas para enfermedad arterial oclusiva severa y ausencia de enfermedad arterial oclusiva. Mediante esta metodología se obtienen valores matemáticos que dan cuenta de la dinámica fractal de la ramificación coronaria izquierda, evidenciando así el impacto de la lesión en la totalidad de la ramificación. Con las definiciones de variabilidad y diferencia neta de las dimensiones fractales como medida morfométrica, se evidenció que los grupos de pacientes sin enfermedad arterial oclusiva y con enfermedad arterial oclusiva moderada, presentan similitud en su comportamiento, lo cual se caracteriza por una mayor variabilidad, con diferencias netas generalmente diferentes de 0, en comparación con los pacientes con enfermedad arterial oclusiva severa, donde este comportamiento se invierte; con estos resultados posiblemente puedan desarrollarse mediciones de impacto diagnóstico.

Al observar los cambios después de la primera cifra decimal entre cada una de las medidas consecutivas, se observa una variabilidad entre 0 y 4 décimas. Sin embargo, el cálculo de la diferencia neta se realiza con los cambios de dos y tres décimas, puesto que los cambios de una décima aparecen indistintamente en los grupos y sólo se presenta un cambio de cuatro décimas, que corresponde al paciente tres del grupo 3. El concepto de diferencia neta proporciona un único número que sintetiza la información de cada secuencia de imágenes. El análisis de las diferencias y similitudes entre los grupos, se basa en la observación del número de diferencias netas de 0 que aparecen en cada grupo, con respecto a las diferencias netas diferentes de 0, de este modo se evidencia el aumento o disminución de la variabilidad, puesto que la observación aislada de las diferencias netas no permite establecer características distintivas entre los grupos.

Anteriormente, se aplicó esta metodología a grupos de pacientes con y sin enfermedad arterial oclusiva, mostrando que la variabilidad y diferencia neta son conceptos que permiten diferenciar estos dos grupos de forma general. En este trabajo se evaluó la enfermedad arterial oclusiva moderada y se encontró que con esta generalización metodológica se obvian las diferencias cualitativas y diagnósticas convencionales entre ausencia y presencia de enfermedad arterial oclusiva, por la similitud matemática encontrada entre enfermedad arterial oclusiva moderada y ausencia de enfermedad arterial oclusiva. En otros trabajos de aplicación de teorías matemáticas, tales como la teoría del caos, la geometría fractal o la teoría de la probabilidad a la fisiología humana, se han logrado caracterizaciones objetivas. Este es el caso del análisis de la variación de la frecuencia cardiaca fetal realizada por Rodríguez y colaboradores (23) a partir de la definición de componentes dinámicos del sistema, en el cual se obtiene una medida objetiva y reproducible de esta dinámica. En estudios de dinámica caótica se han establecido diferencias entre salud y enfermedad (16, 24-30). Estos trabajos se basan en la observación de la dinámica cardiaca, mientras que en la presente investigación se realiza un análisis geométrico de los cambios durante el movimiento cardiaco, con el cual se obtiene la dinámica fractal de un mismo objeto.

El concepto de armonía matemática intrínseca, desarrollado por Rodríguez y colaboradores (9), permite la determinación de relaciones entre varias medidas fractales de un mismo objeto, obteniendo un resultado de aplicación experimental efectiva. Al realizar una caracterización de la ramificación solamente con dimensiones fractales aisladas, no se tiene en cuenta la dinámica del objeto. En este trabajo al aplicar los conceptos de variabilidad y diferencia neta para el análisis de imágenes angiográficas, se tiene en cuenta no sólo el impacto de la obstrucción respecto a la totalidad sino además el cambio de la estructura geométrica en el tiempo. Este tipo de metodologías provee formas originales de sintetizar múltiple información obtenida de un fenómeno, además de ser independientes de procedimientos estadísticos que resultan mucho más costosos por requerir de un gran tamaño muestral.

Al observar los grupos 1 y 2, se encuentran diferencias netas de cero en cuatro ocasiones, correspondientes respectivamente al caso 4 del grupo 1 y a los casos 5, 8 y 9 del grupo 2, diferenciándose del comportamiento variable que caracteriza estos grupos en general. Del mismo modo, los pacientes 4 y 5 del grupo 3 presentaron diferencias netas mayores a cero, en contraposición a lo que se observa en el resto de pacientes del grupo. Es posible que esto ocurra porque los pacientes además de manifestar enfermedad arterial oclusiva moderada o severa, pueden presentar diferentes patologías como hipertensión arterial o cardiomiopatía dilatada, entre otras, simultáneamente; del mismo modo, los pacientes con ausencia de enfermedad arterial oclusiva pueden presentar otras patologías cardiacas, pues la angiografía es un examen invasivo que sólo se realiza a pacientes cuyo estado clínico amerita esta intervención. Las excepciones encontradas con respecto al comportamiento general en cada uno de los grupos, probablemente se relacionan con los cambios geométricos del corazón afines con las diferentes patologías.

En la actualidad no existe una metodología de aplicación clínica que integre la información de los exámenes que evalúan la fisiología y la morfología cardiaca, por lo cual la interpretación de los múltiples resultados para obtener un diagnóstico global, depende de la experiencia y subjetividad médica. Es de suponer que una adecuada caracterización y evaluación de diferentes exámenes a nivel morfológico y fisiológico, servirá como base para el desarrollo de una metodología diagnóstica unificada de los mismos. Haciendo uso de simulaciones como las realizadas por Kappenberger (31) respecto a la actividad cardiaca, que muestran cómo la geometría y la anatomía influyen en la estabilidad eléctrica del corazón, sería posible efectuar una mejor evaluación del paciente a partir del análisis matemático unificado de diferentes exámenes que brinden un diagnóstico global y objetivo que dé cuenta del estado de cada paciente particular en la práctica clínica.

Aplicaciones futuras

La generalización de esta metodología de evaluación a partir del estudio del comportamiento de la dinámica cardiovascular de pacientes con enfermedad arterial oclusiva leve, posiblemente permitirá obtener diagnósticos cuantificables con aplicación clínica y valoraciones acordes con el estado de la ramificación coronaria izquierda para cada caso individual, independientemente de la patología presentada.

Por tratarse de aplicaciones matemáticas que dan cuenta de la dinámica fractal de la totalidad de la ramificación coronaria izquierda y no sólo de una parte, este trabajo facilitará la realización de simulaciones computacionales de esta dinámica.

Conclusiones

La metodología aplicada constituye una medida adecuada para la ramificación coronaria izquierda con enfermedad arterial oclusiva moderada, severa y sin enfermedad arterial oclusiva, permitiendo una caracterización de la dinámica total de la ramificación coronaria.

Los pacientes con enfermedad arterial oclusiva moderada presentan una variabilidad matemáticamente similar a la de los pacientes sin enfermedad arterial oclusiva, al presentar diferencias netas generalmente diferentes de cero, siendo diferenciables de los pacientes con enfermedad arterial oclusiva severa, caracterizados en general por una variabilidad igual a cero.

En los grupos de pacientes con enfermedad arterial oclusiva moderada y ausencia de enfermedad arterial oclusiva, los valores de diferencia neta que se encuentran con mayor frecuencia son los de dos.

El uso de teorías matemáticas hace posible obtener resultados concluyentes sin necesidad de un gran volumen poblacional ni tratamientos estadísticos, lo que optimiza esfuerzos y recursos.

Agradecimientos

A la Fundación Cardioinfantil - Instituto de Cardiología, en especial, Al Dr. Darío Echeverri, del Departamento de Hemodinamia, por apoyar las investigaciones del grupo INSIGHT.
Al Dr. Emilio Osorio, por colaborar con el conocimiento clínico actual en enfermedad arterial oclusiva.
A Adriana Forero, por su incondicional apoyo al grupo INSIGHT.
A Doris Páez, por su colaboración con el grupo INSIGHT.

Bibliografía

1. Mandelbrot B. Introducción. En: Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 13-26.        [ Links ]

2. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 27–50.        [ Links ]

3. Mandelbrot B. The fractal geometry of nature. San Francisco: Freeman; 1972. p. 341-8.        [ Links ]

4. Abkyankar A, Copeland LS, Wong W. Nonlinear dynamics in real-time equity market indices: evidence from the United Kingdom. The Economic Journal 1995; 105: 864-80.         [ Links ]

5. Chu PK. Study on the non-random and chaotic behavior of chinese equities market. Review of Pacific Basin Financial Markets and Policies 2003; 6 (2): 199-222.        [ Links ]

6. West JW. Fractal physiology and chaos in medicine. Singapore: World Scientific; 1990.        [ Links ]

7. Pohlman S, Powell K, Obuchowski NA. Quantitative classification of breast tumors in digitized mammograms. Med Phys 1996; 23: 1337-1345.        [ Links ]

8. Lefebvre F, Benali H. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995; 22: 381-390.        [ Links ]

9. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis: armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol 2002; 10: 65-72.        [ Links ]

10. Huikuri HV, Makikallio TH, Peng Ch, Goldberger AL, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infartion. Circulation 2000; 101: 47-53.        [ Links ]

11. Glenny H, Robb W, Robertson H, Thomas, Yamashiro, Stanley, Bassingtewaighte JB. Applications of fractal analysis to physiology. J Appl Physicl 1991; 70 (6): 2351-67.        [ Links ]

12. Burgos J. Fractal representation of the immune B cell repertoire. Biosystems 1996; 39: 19-24.         [ Links ]

13. Burgos J, Moreno-Tovar P. Zipf-scaling behavior in the immune system. Biosystems 1996; 39: 227-32.         [ Links ]

14. Landini G, Rippin JW. Fractal dimensions of epithelial-connective tissue interfaces in premalignant and malignant ephitelial lesions of the floor of mouth. Anal Quant Cytol Histol 1993; 15: 144-149.        [ Links ]

15. Luzi P, Bianciardi G, Miracco C, De Santi MM, Del Vecchio MT, Alia L, et al. Fractal analysis in human pathology. Ann N Y Acad Sci 1999; 879: 255-7.        [ Links ]

16. Goldberger AL, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS 2002; 99: 2466-2472.        [ Links ]

17. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alergeno Poa P9. Rev Fac Med Univ Nac Colomb 2005; 53 (2): 72-8.        [ Links ]

18. American Heart Association. Heart disease and stroke statistics, 2003 update. Dallas (Tex): American Heart Association; 2002.        [ Links ]

19. Rodríguez J, Álvarez L, Mariño M, Avilán G, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Dinámica fractal de la ramificación coronaria. Rev Col Cardiol 2004; 11 (4): 185-92.        [ Links ]

20. Peitgen H, Jurgens H, Saupe D. Chaos and fractals; new frontiers of science. New York: Springer; 1992.        [ Links ]

21. Rozo R, Merchán A, Calderón J. Cardiología. 1ª. edición. Bogotá: Ediciones Médicas Latinoamericanas; 1999.        [ Links ]

22. Braunwald E. Heart disease. 5a. Ed. Philadelphia, Pennsylvania: W.B. Saunders Company; 1997. p. 266-8.        [ Links ]

23. Rodríguez J, Carmona V, Avilán N, Hincapié P. Análisis de la monitoría fetal con la teoría de la probabilidad. Rev Col Obs Gin 2004; 55 (4): 267-278.        [ Links ]

24. Grebogi C, Ott E, Yorke J. Chaos, strange attractors, and fractal brasin boundaries in nonlinear dynamics. Science 1987; 238: 631-637.        [ Links ]

25. Grassberger P, Proccacia I. Characterization of strange attractors. Physical Review Letters 1983; 50 (5): 346-349.        [ Links ]

26. Garfinkel A, Spano M, Ditto W, Weiss J. Controlling cardiac chaos. (Research Articles) Science 1992; 257: 1230-1235.        [ Links ]

27. Goldberger AL. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet 1996; 347: 1312-1314.        [ Links ]

28. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990; 262: 42-49.        [ Links ]

29. Plamen I, Rosenblum M, Peng CK, Mietus J, Havlin S, Stanley H, et al. Scaling behavior of heartbeat Intervals obtained by wavelet-based time-series analysis. (Letters to Nature) Nature 1996; 383: 323-327.        [ Links ]

30. Glass Leon. Complex cardiac rhytms. (News and Views) Nature 1987; 330: 695-696.        [ Links ]

31. Kappenberger L. Arrythmia: a therapeutic dilemma. En: Computer Simulation and Experimental Assessment of Cardiac Electrophysiology. Futura Publishing Company, Lausanne; 2001. p. 185-188.        [ Links ]

¹ Definición original del primer autor.
² Definición original del primer autor.