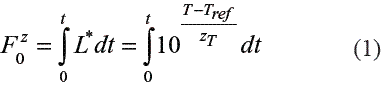Fenomenología de la esterilización de alimentos líquidos enlatados

Transport behavior of sterilization of canned liquid-food

Juan Alvarado, Gloria Martínez, José Navarrete, Enrique Botello, Mario Calderón, Hugo Jiménez^*

Departamento de Ingeniería Química-Bioquímica, Instituto Tecnológico de Celaya Ave. Tecnológico y Antonio García Cubas s/n, C.P. 38010, Celaya, Gto. México

 

---

Resumen

Esta revisión presenta una perspectiva sobre la evolución de la esterilización térmica de alimentos líquidos enlatados y la importancia que la modelación matemática y el análisis numérico computacional han tenido en la estimación del tiempo de esterilización equivalente.

Palabras clave: Navier-Stokes, esterilización de alimentos, zona de calentamiento más lento (ZCL)

 

---

Abstract

A perspective on the evolution of liquid-food thermal sterilization and the importance of mathematical modeling and the role of computational numerical analysis in the estimation of equivalent sterilization time is presented in this work.

Keywords: Navier-Stokes, food sterilization, slowest heating zone (SHZ)

 

---

Introducción

La esterilización térmica de alimentos envasados es aún la técnica mas aplicada en la preservación de alimentos, desde que fue aplicada por Nicolás Appert en 1810, independientemente del desarrollo de tecnologías alternativas denominadas tratamientos no térmicos (campo de pulsos eléctricos, alta presión hidrostática, UV, entre otros) [1]. Representa además, entre el 10 y 15% de las manufacturas totales y es uno de los procesos industriales de mayor consumo energético e inversión de capital [2], razones por las que gran cantidad de estudios han sido enfocados a la mejora de los procesos térmicos, con la finalidad de garantizar esterilidad comercial, minimizar costos, maximizar la retención de nutrientes y optimizar los recursos energéticos. Su objetivo es procesar alimentos seguros, de alta calidad y a un precio que el consumidor esté dispuesto a erogar [3].

El diseño de un proceso térmico, requiere la selección del microorganismo a inactivar relacionado con el producto alimenticio. Para alimentos de baja acidez (pH > 4.6), se da una atención especial a Clostridium botulinum, microorganismo formador de esporas altamente resistentes al calor y productor de una toxina letal para el hombre. The National Canners Association define un valor mínimo para la esterilización comercial igual a doce veces el tiempo de reducción decimal (valor 12D) [4], con el fin de garantizar que un alimento enlatado es seguro para su consumo. La esterilización de alimentos no es selectiva por lo que las pérdidas del valor nutricional y sensorial del alimento son inherentes al proceso. El diseño eficiente de un proceso térmico, requiere del conocimiento de cinéticas de destrucción de microorganismos, enzimas y nutrientes asociados a la calidad del alimento, además del historial de temperatura de la zona de calentamiento más lento (ZCL) del envase, cuya ubicación ha sido tradicionalmente medida usando termopares fijados en diversos puntos dentro del envase, lo que favorece los errores de medición asociados a la perturbación de los patrones de flujo y el incremento del área de transferencia de calor, además de que la ZCL no se mantiene fija [5] y su trayectoria depende de la forma y orientación del envase, las propiedades termodinámicas del alimento y de la dinámica de calentamiento [6].

Si la transferencia de calor es controlada por conducción, la ZCL se localizará en el centro geométrico del envase, teniendo poco efecto sobre su ubicación, la dependencia de las propiedades termodinámicas con la temperatura [6, 7]. La convección natural por su parte, provoca que la ZCL migre hacia el fondo del envase durante el proceso térmico, desplazándose hacia el eje axial y luego hacia el centro de la lata, para ubicarse en una región localizada 0 < r < R y 0 < z < L/5, al final del proceso [5]. La dificultad de ubicar la ZCL para alimentos líquidos y los errores asociados al uso de termopares, han generado interés en el entendimiento de los fenómenos de transporte asociados a dicho proceso, lo que implica la solución numérica de las ecuaciones de conservación de momentum, energía y masa de manera acoplada. La solución no hubiera sido posible, sin la evolución de los sistemas de cómputo, que permitieron el desarrollo de software de dinámica computacional de fluidos (CFD) [8], altamente especializado (PHOENICS, Fluent, FIDAP, Femlab, entre otros). La simulación numérica provee información más detallada y precisa sobre la distribución de temperatura y patrones de flujo dentro del envase [9]. CFD es una herramienta numérica robusta que se está utilizando ampliamente para simular procesos en la industria de alimentos [8].

Por otra parte, se requiere conocer la dinámica de penetración de calor en la ZCL del envase para determinar el grado de esterilización asociado al proceso o el tiempo de procesamiento requerido para obtener esterilidad comercial usando el Método General de Bigelow o el Método de Fórmula de Ball, los cuales son las técnicas más utilizadas en el cálculo de procesos térmicos [10], que dependen de mediciones experimentales, lo que limita su capacidad predictiva y de análisis de sensibilidad.

Procesamiento térmico de alimentos

Debido a la cinética de primer orden que sigue la inactivación microbiana es prácticamente imposible la obtención de un producto estéril. La destrucción completa de formas viables, representaría la destrucción del alimento [11]. Los tratamientos térmicos además de inactivar microorganismos, también destruyen algunas vitaminas termolábiles (Tiamina) y promueven la oxidación de lípidos [12]. Los efectos del calor sobre proteínas y lípidos han sido descritos con detalle por Mauron en 1982, Witting y Dimick en 1982 [13,14]. Un procesamiento térmico efectivo, se basa en la definición de esterilización comercial emitida por la Food and Drug Administration (FDA, USA): “La aplicación de calor al alimento, antes o después de ser empacado en un contenedor sellado herméticamente, por un periodo de tiempo y a una temperatura determinada, que garantice la destrucción de microorganismos que puedan dañar la salud de los consumidores”. En México, la norma oficial NOM-130-SSA1-1995 define a la esterilización comercial como el tratamiento térmico aplicado al producto para la destrucción de todos los microorganismos viables de importancia en la salud pública y aquellos capaces de reproducirse en el alimento bajo condiciones normales de almacenamiento y distribución, sin la condición de refrigeración.

Tipos de tratamientos térmicos

Actualmente son dos los tipos de procesos térmicos más utilizados por la industria alimentaria: el proceso aséptico y el enlatado. En el procesamiento aséptico, el alimento líquido se esteriliza fuera de la lata, seguido de un envasado y sellado en condiciones asépticas. Este proceso ofrece un producto de alta calidad, pero es más costoso. Las temperaturas pueden ser tan altas como 150^oC, alcanzándose la esterilización comercial en un tiempo de 1 o 2 segundos [15, 16]. En el caso del enlatado, el alimento es esterilizado una vez que ha sido envasado (llenado, eliminación de aire con vapor y engargolado). El enlatado es un proceso lento e ineficiente comparado con el proceso aséptico. Sin embargo, los problemas de costo y de la manipulación y llenado de algunos tipos de alimentos tales como espárragos o encurtidos, y la incapacidad de bombear otro tipo de productos alimenticios, debido a su consistencia física, son algunas razones de que la gran mayoría de productos son esterilizados después de envasarlos [17].

Factores que determinan la condición del procesamiento térmico

Los factores más importantes que determinan las condiciones del proceso térmico son: el tipo de microorganismo, pH del alimento, composición del alimento, condiciones de calentamiento, medio de calentamiento, tipo de contenedor, forma y tamaño.

Tiempo de reducción decimal (D)

El tiempo de reducción decimal (D) se define como el tiempo de procesamiento aplicado a una población microbiana a temperatura constante, requerido para inactivar el 90% de la población con cinética de muerte de primer orden [18]. Para C. botulinum D = 0,21 min a 121,1^oC.

Valor z_T

El valor z_T se expresa como la diferencia de temperatura requerida para un cambio decimal en el valor D. Por lo tanto, el tiempo de reducción decimal y el factor z_T se requieren en la descripción de la cinética de inactivación térmica de esporas bacterianas, teniendo el mismo papel que la constante de velocidad y la energía de activación E_a en la ecuación de Arrhenius [14].

Letalidad de un proceso de tratamiento térmico

La letalidad L^* se define como el tiempo de calentamiento equivalente a una temperatura de referencia T_ref, con respecto a un minuto de calentamiento a una temperatura T, en donde T_ref toma usualmente el valor de 121,1^oC (250^oF) para procesos de esterilización y el valor de z_T está en función de la especie de microorganismo (Para C. botulinum z_T es igual a 10^o C). Para un proceso en el cual el producto alimenticio está sujeto a un perfil de temperatura-tiempo, la velocidad letal se integra sobre el tiempo de procesamiento para obtener la letalidad del proceso completo, como se muestra en la ecuación (1):

La letalidad equivalente F permite decidir si un tratamiento térmico en particular es seguro para garantizar esterilidad comercial. Existen tablas de valores F recomendados para una gran diversidad de alimentos [4].

Teoría de penetración de calor

Para estimar el tiempo de proceso para un alimento con el fin de asegurar esterilización comercial y calidad deseada, se deben conocer los datos de penetración de calor para la ZCL. Tradicionalmente esta temperatura se determina mediante el uso de termopares, aunque en la actualidad, el desarrollo de la computación, ha permitido el desarrollo de software CFD, (PHOENICS, Fluent, FIDAP, Femlab, CFX entre otros), que han facilitado la solución numérica de las ecuaciones de transporte asociadas al proceso térmico.

Los termopares

La inserción de termopares en la lata para ubicar la ZCL origina distorsión en los patrones de flujo en alimentos líquidos que presentan mecanismos convectivos, resultando en mayores coeficientes de transferencia de calor, afectando los gradientes de temperatura en las direcciones radial y axial de la lata que, en condiciones normales no existirían [6].

Mongkhonsi [19] en un estudio en reactores de lecho fijo, sugiere que la distorsión se origina por la pérdida de calor en la superficie del reactor debido a la presencia de los termopares, los cuales proporcionan un área de transferencia de calor adicional, que tiene el efecto de una aleta de enfriamiento en un intercambiador de calor. Zhang [20] en un estudio experimental con termopares Eklund^MR, reporta que su inserción en la lata, tiende a aumentar la tasa de penetración de calor y, por lo tanto a subestimar los tiempos de tratamiento térmico alrededor de un 5 %. La situación anterior causa incertidumbre sobre la ubicación del punto frío, con el riesgo de que el alimento no sea procesado adecuadamente, lo cual es más crítico sí se manifiestan mecanismos de convección-conducción [5], que van variando conforme el alimento se va calentando [6]. Por otra parte, se han desarrollado dispositivos inalámbricos para la detección de temperaturas dentro de la lata [21], pero no necesariamente seguirían la trayectoria de la ZCL, sino la de las corrientes de convección.

Métodos de cálculo de los procesos térmicos

Los métodos para el cálculo del proceso térmico se dividen dos grupos: método general y métodos Fórmula. El método general propuesto por Bigelow [22] y mejorado más tarde por Ball [23], se aplica a datos reales o simulados de tiempotemperatura, resultado del análisis de penetración de calor para los envases evaluados. Para integrar los efectos letales asociados al proceso se resuelve la ecuación (1) de manera gráfica o numérica. Este método es el más preciso para condiciones experimentales, tiene la versatilidad de aplicarse a cualquier mecanismo de transferencia de calor, sin embargo está restringido a las condiciones bajo las cuales fueron medidos los datos de penetración de calor y cualquier cambio en las condiciones de procesamiento como: la temperatura del medio de calentamiento, temperatura inicial del producto, tamaño del envase, requiere de determinar nuevamente el perfil de temperatura correspondiente en la ZCL, lo que no permite extrapolar resultados ni efectuar análisis de sensibilidad.

Fundamentos de la transferencia de calor en alimentos envasados

Conducción

La conducción de calor en alimentos enlatados, se debe al intercambio de energía cinética de las moléculas con mayor energía, que se encuentran más cerca de las paredes del envase, a las moléculas adyacentes de menor energía. La energía se transmite hacia al centro geométrico del envase donde se localiza la ZCL [24]. Alimentos como atún enlatado, patés, algunas cremas y pastas normalmente se consideran calentados por conducción. Por lo tanto, el tiempo requerido de procesamiento se determina a partir de la solución analítica o numérica de la ecuación de Laplace en 2-D (coordenadas radial y axial) ó midiendo experimentalmente la temperatura en el centro de las latas.

Convección natural

La convección natural en alimentos enlatados, se produce por los gradientes de temperatura generados entre la superficie del envase y el líquido que contiene. Se presenta principalmente en alimentos líquidos diluidos o con sólidos suspendidos, como: leche condensada, puré de tomate, sopas, cremas, caldos y jugos, entre muchos otros. Las ecuaciones de transporte de momentum y energía, deben resolverse de manera simultánea, lo que dificulta su análisis y en consecuencia, la mayoría de los problemas que implican el fenómeno convectivo se estudian de manera experimental y los resultados se presentan de forma empírica, con grupos adimensionales como: Reynolds (Re), Prandtl (Pr), Nusselt (Nu), Grashof (Gr) y Rayleigh (Ra) los cuales aparecen de manera natural en el desarrollo y adimensionalización de las ecuaciones de transporte de momentum y de calor [24]. Welti-Chanes [24] presenta una revisión de las diferentes correlaciones del tipo Nu = f (Re, Pr, Gr) con sus aplicaciones en el tratamiento térmico de alimentos. Kannan [25] reporta diversas correlaciones para estimar el número de Nusselt (Nu) en función del número de Fourier (Fo), del aspecto geométrico de la lata y la conductividad térmica del alimento.

Flujo de fluidos y modelos reológicos

Cuando se considera el flujo en productos alimenticios, es necesario tomar en cuenta su naturaleza reológica, ya que dictamina el comportamiento de flujo. Los fluidos son clasificados principalmente en dos grandes grupos: Newtonianos y no-Newtonianos. Los primeros exhiben una relación lineal entre el esfuerzo de corte y la velocidad de deformación, mientras que los fluidos no Newtonianos son los que se desvían del comportamiento newtoniano. La mayoría de los alimentos exhiben alguna forma de comportamiento no-Newtoniano y muchos modelos de flujo han sido utilizados para describir tal comportamiento Los dos modelos más comúnmente usados son: La ley de la Potencia y el modelo de Herschel-Bulkley [26, 27].

Modelos matemáticos y su solución para procesos de esterilización de alimentos enlatados

Las leyes de conservación de momentum, energía y masa aplicadas al transporte de fluidos, describen las variaciones de velocidad, temperatura y concentración con respecto al tiempo y posición en el sistema en cuestión.

Modelación matemática de la convección natural en latas cilíndricas en 2-D

En la modelación, se considera una lata individual de radio R y altura L, la cual se encuentra a una temperatura inicial T_o, que contiene un alimento constituido por un fluido homogéneo. Esta lata se esterilizará en una autoclave estacionaria a una temperatura de operación T_r y con un coeficiente de transferencia de calor por convección h_c conocido. Algunas de las consideraciones usuales para establecer un nivel de sofisticación del modelo son: Caso axisimétrico que permite modelar un problema originalmente en 3-D como uno en 2-D; fluido en régimen laminar, Newtoniano, isotrópico; propiedades constantes durante el proceso, excepto la densidad en el término de fuerzas volumétricas de la ecuación de momentum (aproximación de Boussinesq); disipación viscosa despreciable (degradación de energía mecánica); es una cavidad con fronteras rígidas e impermeables y, por lo tanto no se presenta deslizamiento; la resistencia térmica del envase puede despreciarse; la existencia de un espacio de cabeza en la parte superior de la lata que origina una disminución del coeficiente convectivo de transferencia de calor [28, 29]. Existen diversas formas de tratamiento de las ecuaciones gobernantes de la convección natural en 2-D, de las cuales se mencionan las siguientes:

Ecuaciones en Variables Primitivas

Se tendrán cuatro ecuaciones en función de cuatro variables dependientes: la velocidad del fluido en dirección r, la velocidad del fluido en dirección z, la presión y la temperatura, conocidas como variables primitivas, las tres primeras derivadas de las ecuaciones de Navier-Stokes [30].

La principal dificultad de solución de las ecuaciones de Navier-Stokes, es la elección de las condiciones de frontera para la presión, ya que está en función de la temperatura y de la densidad, lo que complica el problema. Además, los términos de primer orden de la ecuación de continuidad provocan inestabilidad numérica [31], requiriéndose mayor investigación con el fin de encontrar una manera idónea de evitar esta inestabilidad. Algunas posibles alternativas serían: la utilización de métodos de diferencias finitas de mayor orden; el mapeo de la ecuación de continuidad, análisis de malleo o la valoración de otras técnicas de discretización como residuos ponderados, elemento finito y volumen finito de control [32].

Función corriente y vorticidad

Este método elimina el término de gradiente de presión de la ecuación de balance de momentum por diferenciación cruzada (aplicación del rotacional). Esto conduce a la obtención de una ecuación de vorticidad para el caso de medios homogéneos o de medios porosos modelados con la ley de Darcy con la extensión de Brinkman. Posteriormente, utilizando la definición de función corriente [33], se elimina la ecuación de continuidad. La solución del modelo de transporte se obtiene en términos de función corriente, vorticidad y temperatura. Los valores de la función corriente permiten graficar las líneas de corriente en la cavidad, lo que es importante en el análisis en fenómenos de convección natural. Un problema es la determinación de las condiciones de frontera de la vorticidad por lo que algunos autores han propuesto diversas formas para estimarlas, tales como las aproximaciones de Woods, Toms o Jensen [34] cuya deducción parte de la ecuación de vorticidad [32,35, 36]. Jiménez-Islas [5] reporta la modelación del problema axisimétrico 2-D para alimentos que contienen partículas en suspensión, empleando la metodología anterior.

Aproximación de Boussinesq

En sistemas en donde la convección natural es el mecanismo de transporte de calor predominante, la variación de la densidad con la temperatura tiene una importancia crítica y es conveniente modificar la ecuación de momentum para tener en cuenta los efectos del empuje o flotación [37]. Para simplificar la solución numérica, algunos autores recomiendan emplear la aproximación de Boussinesq, que consiste en considerar a la densidad constante, excepto en el término de fuerzas volumétricas [32, 33, 38]. Desarrollando mediante series de Taylor, alrededor de un valor medio, despreciando los términos superiores a la primera derivada e introduciendo la definición de la expansión volumétrica β, se obtiene la ecuación (2) que corresponde a la aproximación de Boussinesq, que ha sido extensamente validada [38]

.

Modelación para predecir la dinámica de calentamiento y los patrones de flujo en alimentos enlatados

Hasta hace unos 30 años, la mayoría de los análisis matemáticos eran desarrollados para alimentos calentados por conducción únicamente, debido a la simplicidad de las soluciones analíticas o numéricas. En el calentamiento por convección natural, la velocidad de movimiento está acoplada con la temperatura y la concentración de masa respectivamente. Este acoplamiento implica la solución simultánea de las ecuaciones diferenciales parciales (EDP) de continuidad, momentum, energía y las ecuaciones de masa asociadas (microorganismos, nutrientes). Estas consideraciones convierten al sistema en un problema de convergencia difícil ya que la estabilidad del método dependerá principalmente del número de Ra, del tamaño de malla, del método de discretización espacial y de las etapas de integración en el tiempo [32, 39]. P. M. Stevens [24, 40] fue el primero en presentar una solución numérica para los sistemas de EDP que gobiernan el calentamiento por convección natural en alimentos líquidos envasados [24]. Datta [41] resolvieron numéricamente las ecuaciones unidireccionales gobernantes de la transferencia de calor convectivo de un fluido en un recipiente de radio R y longitud Z. Estos investigadores involucraron las ecuaciones de continuidad números adimensionales para un cilindro finito, para calcular el coeficiente convectivo de calor [41]. Posteriormente Datta [42] llevaron a cabo predicciones numéricas de los perfiles de temperatura y velocidad en estado dinámico para una autoclave estacionaria, durante el calentamiento por convección natural de agua como fluido de trabajo. Predijeron además una circulación interna en el fondo de la lata y mostraron que, la ZCL tiene una forma pseudo-toroidal, localizada cerca del fondo de la lata, alrededor de un décima parte de la altura de la misma [42].

Kumar [29], Kumar [43] desarrollaron simulaciones para la esterilización de líquidos viscosos en latas cilíndricas, dispuestas verticalmente y calentadas en una retorta estacionaria. Resolvieron las EDP de continuidad, cantidad de movimiento y energía para un caso axisimétrico, generando gráficos de temperatura y velocidad de líneas de corriente para calentamiento por convección natural, comparando sus resultados con los gráficos para conducción pura. Sus resultados muestran como las corrientes de convección formadas dentro del envase empujan la ZCL hacia el fondo de la lata. Ghani [44] simularon la esterilización para una lata con una solución de Carboximetil celulosa (CMC) como fluido de trabajo dispuesta verticalmente. El medio de calentamiento fue vapor saturado. La diferencia de temperatura para el domo y fondo de la lata al final del proceso (2574 s) fue de 12^oC para la lata aislada y 10^oC para la calentada completamente. Los resultados muestran que la ubicación de la ZCL es similar en ambos casos. Esto se debe al efecto intenso de las corrientes de convección natural, aún inclusive cuando el líquido es muy viscoso.

Ghani [39] hicieron simulaciones para CMC y agua, resolviendo las ecuaciones gobernantes de continuidad, momentum y energía para un caso axisimétrico, utilizando PHOENICS. Los resultados muestran que la acción de la convección natural produce la migración del punto frío hacia al fondo de la lata tal como se esperaba. La forma y tamaño de la zona de calentamiento más lento (ZCL) varió según el líquido simulado. Las magnitudes de la velocidades axiales en el proceso térmico fueron encontradas en el rango de 10^-5- 10^-4 m/s para CMC y 10^-2-10^-1 m/s para el agua. Ghani [39] también reportan que, entre menos viscoso es el fluido de trabajo, mayor número de iteraciones se requieren para alcanzar convergencia, lo cual fue corroborado por Jiménez-Islas [5].

Ghani [45] usaron PHOENICS para predecir la distribución de temperatura y la concentración de bacterias viables en una lata. Las ecuaciones gobernantes (continuidad, momentum y energía) fueron resueltas junto con la ecuación de balance de concentración de C. botulinum usando el método de volumen finito. Una cinética de primer orden se utilizó para describir la inactivación microbiana. Se usó CMC como fluido de trabajo en una lata cilíndrica. El medio de calentamiento fue vapor saturado a 121.1^oC y el modelo también consideró la viscosidad dependiente de la temperatura y la aproximación de Boussinesq para la densidad. Los resultados de la simulación mostraron que la ZCL se localizó alrededor del 10 %-15 % de la altura de la lata. El efecto de la difusión sobre la velocidad de esterilización fue encontrado como despreciable para el caso de estudio. Siriwattanayotin [46] emplean CFX para estudiar numéricamente los cambios de concentración de azúcar invertido que se asocia como un indicador de la inactivación térmica de los microorganismos. Ghani [47] extendieron el trabajo previo presentado por Ghani [39] estudiando la esterilización de alimentos en latas en disposición vertical con respecto a la esterilización en latas en disposición horizontal, lo que convierte un problema en 2-D a uno en 3-D debido a la pérdida de la axisimetría inherente en latas en orientación vertical. El fluido usado fue sopa de zanahorianaranja, considerado como fluido newtoniano. Las ecuaciones gobernantes se resolvieron con el método de volumen finito usando PHOENICS. Los resultados muestran como la zona de calentamiento más lento disminuye gradualmente y desciende desde la mitad de la lata hacia el fondo de la misma. La ZCL se mantuvo en movimiento durante el proceso térmico, ubicándose al final del proceso en una región alrededor del 20-25% de la altura de la lata. Varma [48] desarrollaron un estudio comparativo de los tiempos de esterilización requeridos para alcanzar una temperatura de procesamiento de 100^oC para diversas geometrías (cilindros, conos y conos truncados) en envases de igual volumen, usando como fluido de trabajo una solución con comportamiento pseudoplástico de CMC (0.85% en peso). Se observó un menor tiempo de esterilización para la orientación vertical de la lata cónica (con la arista hacia abajo). El cilindro produjo un menor tiempo de esterilización cuando se orienta horizontalmente con respecto a su orientación vertical. El tiempo requerido para alcanzar la temperatura de proceso (100^oC) en la zona de calentamiento más lento, tomó 1098 s para el cono y 1288 s para el cilindro en disposición vertical (con la arista hacia abajo). Cuando el ángulo de orientación se giró 180^o, el cilindro representó la mejor geometría con respecto al cono (arista hacia arriba), con 1424.5 s y 1560.5 s respectivamente. La ZCL para todas las geometrías se ubicó al final del proceso a un 10% con respecto de la altura total del envase.

Jiménez-Islas [5] desarrollaron un código computacional para determinar la dinámica y la ubicación del punto frío, en latas cilíndricas usando autoclaves estacionarias. Las ecuaciones gobernantes se discretizaron usando colocación ortogonal con polinomios de Jacobi para intervalos de malleo entre 21x21 a 43x43, con 100 a 1000 etapas de integración, mientras el tiempo fue discretizado usando el método de Euler implícito. El sistema algebraico resultante se resolvió mediante relajación no lineal. Como casos de estudio utilizaron alimentos enlatados como atún en agua, frijoles tipo tradicional y chícharos en salmuera. La densidad, calor específico y conductividad térmica se estimaron por el método reportado por Choi [49] a partir de su composición proximal a una temperatura promedio. Sus resultados muestran la formación y migración de la ZCL, ubicándose al final del proceso entre el 10-15 % de la altura de la lata. Todos los investigadores revisados hasta el momento concuerdan en sus resultados obtenidos para el calentamiento por convección natural de envases cilíndricos. Al inicio de la fase de calentamiento, cuando los patrones de flujo no han sido definidos por completo, los perfiles de temperatura obtenidos son muy semejantes a los encontrados en la conducción pura, pero a medida que el tiempo de calentamiento avanza, las fuerzas de flotación producen un flujo ascendente cerca de la pared lateral, el cual se enfría en la parte superior formando la recirculación del líquido.

A tiempos pequeños se presentan flujos secundarios en la parte inferior de la lata con flujo inverso (sentido contrario a las manecillas del reloj), debido al elevado gradiente de temperatura que se presenta en esta región. A medida que el tiempo avanza la intensidad del flujo va disminuyendo debido a que los gradientes de temperatura también se reducen, tendiendo a formar un patrón de flujo unicelular cada vez más lento. Con respecto a las isotermas, al inicio del calentamiento son muy parecidas a los encontradas en los procesos conductivos, pero a medida que el calentamientoavanza, la región más fría se va definiendo, tomando una forma pseudo-toroidal, la cual se desplaza hacia el eje axial de la lata aproximándose a un 10-15 % de la altura del envase para latas en disposición vertical [5, 50]. Sin embargo una discrepancia entre la mejor disposición de la lata (vertical o horizontal), fue observada entre los estudios realizados por Ghani [47], y el realizado por Varma [48]. Estos autores atribuyen la diferencia al uso de un modelo newtoniano para el fluido alimenticio por parte de Ghani [47] en lugar del modelo pseudoplástico utilizado por Varma [48], por lo que se hace patente la necesidad de desarrollar modelos que involucren de manera rigorosa el comportamiento reológico del fluido en cuestión, a partir del balance microscópico de momentum con el fin de deslindar esta contradicción.

Tendencias actuales en los estudios de la esterilización de alimentos líquidos enlatados

La industria de enlatados no siempre tiene las facilidades, especialización o el tiempo, requerido para desarrollar y/o comprender las simulaciones numéricas, por lo que se requiere el desarrollo de nuevas técnicas computacionales o correlaciones que permitan estimar la dinámica de penetración de calor a partir del conocimiento del tipo de alimento (reflejado en un análisis proximal), geometría del envase y de las variables de operación. Se prevé que la investigación debe profundizarse en temas como transferencia de calor y masa en medios porosos y flujo turbulento en la esterilización de alimentos, entre otros problemas [ 51].

Farid [1] aplicaron CFD para latas de diferentes tamaños conteniendo fluidos de diversas viscosidades, para desarrollar una estrategia que permita una estimación de los tiempos de esterilización térmica para nuevos productos o tamaños de latas, proponiendo el uso de una conductividad térmica efectiva, lo que permite reducir el problema a un problema unidireccional, empleando la solución numérica para conducción en cilindro semi-infinito [1]. Chen [52] revisaron la técnica reportada por Farid [1] y ampliaron el trabajo incluyendo la variación del Cp, k, y β con respecto de la temperatura, mejorando la predicción de la temperatura en la ZCL.

Efecto de la viscosidad como función de la temperatura

Como se ha mencionado previamente, existen diversos reportes en donde se ha analizado el efecto de la temperatura sobre la viscosidad μ de manera aproximada, es decir, sustituyendo la funcionalidad de la temperatura en μ en las ecuaciones de Navier- Stokes (que ha sido reducida previamente a partir de la consideración de fluido incompresible para μ y ρ constantes). La manera rigurosa de analizar este efecto es deducir las ecuaciones modificadas de Navier-Stokes a partir del balance microscópico de esfuerzos, tomando en cuenta la diferenciabilidad de μ. Efectuando el desarrollo algebraico correspondiente en coordenadas cilíndricas, se obtienen las ecuaciones modificadas de Navier-Stokes [50]

Componente en dirección r

Componente en dirección θ

Componente en dirección z

En las ecuaciones (3) a (5) se sustituye μ = f(T) para obtener el modelo fenomenológico apropiado. Estas expresiones se pueden reducir a dos dimensiones para casos axisimétricos. Si la viscosidad μ se considera constante, las ecuaciones (3) a (5) se reducen a las ecuaciones clásicas de Navier-Stokes [50].

Conclusiones

En el proceso de esterilización térmica, el avance que representa la llegada de los procesadores de alta velocidad y el desarrollo de modelos matemáticos rigurosos que describen los fenómenos de transporte asociados al tratamiento térmico, han permitido una mejor descripción y cuantificación del proceso de esterilización de alimentos líquidos, lo que hace posible la predictibilidad de los tiempos de esterilización equivalentes y el análisis de sensibilidad. La simulación de diversos escenarios y condiciones de proceso, ha permitido además, la optimización de los recursos energéticos y la calidad del producto, reduciendo así los costos de producción y el ofrecimiento de productos seguros al consumidor.

Agradecimientos

Los autores agradecen el apoyo financiero de CONACYT en su modalidad de Ciencia Básica, con el proyecto SEP-CO1-2004-46230 y de CONCYTEG con el proyecto 07-09-k662-050.

Referencias

1. M. Farid, A. G. Ghani. “A new computational technique for the estimation of sterilization time in canned food”. Chemical engineering and processing. Vol. 43. 2004. pp. 523-531.        [ Links ]

2. I. Dincer. “Heat transfer during heat sterilization and cooling processes of canned products”. International Communications of Heat and Mass Transfer. Vol. 34. 1998. pp. 101-105.        [ Links ]

3. A. G. Ghani. “A computer simulation of heating and cooling liquid food during sterilization process using computational fluid dynamics”. Association for Computing Machinery New Zealand Bulletin. Vol. 2. 2006. pp. 1-14.        [ Links ]

4. National Canners Association. Research Laboratories. “Laboratory Manual for Food Canners and Processors”. Microbiology and Processing. 3^rd ed. The AVI Publishing Company. Inc. Westport, Connecticut. Vol. 1. 1979. pp. 1-336.        [ Links ]

5. H. Jiménez Islas, L. M. González Calderón, J. E. Botello Álvarez, J. L. Navarrete Bolaños. “Estudio Numérico de La Esterilización Térmica de Alimentos Líquidos Enlatados que Contienen Partículas, Empleando el Enfoque de Medio Poroso”. Revista Mexicana de Ingeniería Química. Vol. 4. 2005. pp. 1-23.        [ Links ]

6. M. N. Varma. A. Kannan. “CFD studies on natural convective heating of canned food in conical and cylindrical containers”. Journal of Food Engineering. Vol. 77. 2006. pp. 1024-1036.        [ Links ]

7. C. S. Lucatero. Estudio numérico de la transferencia de calor en la esterilización de alimentos. Tesis de Licenciatura. Instituto Tecnológico de Celaya. Celaya Gto, 2000. pp. 1-103.        [ Links ]

8. T. Norton, D. W. Sun. “Computational fluid dynamics (CFD) - an effective and efficient design and analysis tool for the food industry: A review”. Trends in Food Science & Technology. Vol. 17. 2006. pp. 600-620.        [ Links ]

9. J. Welti-Chanes, F. Vergara-Balderas, D. Bermudez- Aguirre. “Transport phenomena in food engineering: basic concepts and advances”. Journal of Food Engineering. Vol. 67. 2005. pp. 113-128.        [ Links ]

10. D. R. Heldman, D. B. Lund. Handbook of Food Engineering. Marcel Dekker Inc. New York. 1992. pp. 1-756.        [ Links ]

11. P. Valle Vega, R.L. Merson. “Cálculo del tiempo de tratamiento térmico en botes, Método General y Gráfico”. Tecnología de Alimentos Vol. XVI. 1981. pp. 10-22.        [ Links ]

12. E. A. Mulley, C. R. Stumbo, W. M. Hunting. “Thiamine-chemical index of sterilization efficacy of thermal processing”. Journal of Food Science. Vol. 40. 1975. pp. 993-996.        [ Links ]

13. D. B. Lund. “Maximizing nutrient retention”. Food Technology. Vol. 31. 1977. pp. 71-78.        [ Links ]

14. P. J. Fellows. Food Processing Technology. 2^nd ed. Woodhead Publishing Limited. Cambridge. U. K. 2000. pp. 1-608.        [ Links ]

15. N. N. Potter. Food Science. 4^th ed. Ed. Van Nostrand Reinhold, New York. 1986. pp. 169-201.        [ Links ]

16. A. Jung, P. J. Fryer. “Optimising the Quality of Safe Food: Computational Modelling of Continuous Sterilisation Process”. Chemical Engineering Science. Vol. 54. 1999. pp. 717-730.        [ Links ]

17. J. L. Heid, M. A. Joslyn. Food Processing Operations: Their Management, Machines, Materials and Methods 2. AVI Publishing Company Inc.Westport. Connecticut. 1963. pp. 1-644.        [ Links ]

18. J. A. G. Rees, J. Bettison. “Procesado Térmico y Envasado de los Alimentos”. Ed. Acribia. Zaragoza. España. 1991. pp. 1-304.        [ Links ]

19. T. Mongkhonsi, H. F. López Isunza, L. S. Kershenbaum. “The distortion of measured temperature profiles in fixed bed reactors”. Chemical Engineering Research and Design. Vol. 70a. 1992. pp. 255-264.        [ Links ]

20. Z. Zhang. “The effect of thermocouple and receptacle type on observed heating characteristics of conductionheating foods packaged in small metal containers”. Journal of Food Process Engineering. Vol. 25. 2002. pp. 323-335.        [ Links ]

21. F. Marra, V. Romano. “A mathematical model to study the influence of wireless temperature sensor during assessment of canned food sterilization”. Journal of Food Engineering. Vol. 59. 2003. pp. 245-252.        [ Links ]

22. W. C. Bigelow, G. S. Bohart, A. C. Richardson, C. O. Ball. “Heat penetration in processing canned foods”. National Canners Association. Bull I6L. 1920. pp. 1-128.        [ Links ]

23. C. O. Ball. “Thermal Process time for canned food”. Bull. Natl. Res. Council. Vol. 7. 1023. pp. 9-76.        [ Links ]

24. J. Welti Chanes, O. Gómez Palomares, F. Vergara Balderas, S. Maris Alzamora. “Aplicaciones de Ingeniería y Fenómenos de Transporte al Estudio de la Transferencia Convectiva de Calor en Alimentos Envasados”. Revista Mexicana de Ingeniería Química. Vol. 4. 2005. pp. 89-106.        [ Links ]

25. A. Kannan, P. C. G. Sandaka. “Heat transfer analysis of canned food sterilization in a still retort”. Journal of Food Engineering. Vol. 88. 2008. pp. 213-228.        [ Links ]

26. R. B. Bird, R. C. Armstrong, O. Hassager. Dynamics of Polymeric Fluids. Volume 1. Fluid Mechanics. John Wiley & Sons Inc. New York. 1977. pp. 1-450.         [ Links ]

27. J. F. Steffe. Rheological Methods in Food Process Engineering. 2^nd ed. Freeman Press. East Lansing. (MI). 1996. pp. 1-428.        [ Links ]

28. I. O. Mohamed. “Determination of an effective heat transfer coefficients for can headspace during termal sterilization process”. Journal of Food Engineering. Vol. 79. 2007. pp. 1166-1171.        [ Links ]

29. A. Kumar, M. Bhattacharya, J. Blaylock. “Numerical simulation of natural convection heating of canned thick viscous liquid food products”. Journal of Food Science. Vol. 55. 1990. pp. 1403-1411.        [ Links ]

30. R. B. Bird, W. E. Stewart, E. N. Lightfoot. Transport Phenomena. 2^nd ed. John Wiley & Sons Inc. New York. 2002. pp. 1-912. 31. S. V. Patankar, D. B. Spalding. “A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows”. Int. J. Heat Mass Transfer. Vol. 15. 1972. pp. 1787-1806.        [ Links ]         [ Links ]

32. H. Jiménez Islas. Modelamiento Matemático de la Transferencia de Momentum, Calor y Masa en Medios Porosos. Tesis Doctoral. Universidad Autónoma Metropolitana, México D.F. 1999. pp. 1-376.        [ Links ]

33. B. Gebhart, Y. Jaluria, R. L. Mahajan, B. Sammakia. Journal of Buoyancy-Induced Flows and Transport. Hemisphere Publishing Co. New York. 1988. pp. 1-1001.        [ Links ]

34. P. J. Roache. Computational Fluid Dynamics. Hermosa Publishers, Albuquerque, NM. 1972. pp. 1-446.        [ Links ]

35. A. K. Wong, J. A. Reizes. “An Effective Vorticity- Vector Potential Formulation for the Numerical Solution of Three-Dimensional Duct Flow Problems”. J. of Computational Physics. Vol. 55. 1984. pp. 98-114.        [ Links ]

36. A. K. Wong, J. A. Reizes. “The Vector Potential in the Numerical Solution of Three-Dimensional Fluid Dynamics Problems in Multiply Connected Regions”. J. of Computational Physics. Vol. 62. 1986. pp. 124-142.        [ Links ]

37. D. A. Nield, A. Bejan. Convection In Porous Media. Springer-Verlag. New York. 1992. pp. 1-408.        [ Links ]

38. H. Jiménez Islas, J. L. Navarrete Bolaños, E. Botello Álvarez. “Estudio Numérico de la Convección Natural de Calor y Masa 2-D en Granos Almacenados en Silos Cilíndricos”. Agrociencia.Vol. 38. 2004. pp. 325-342.        [ Links ]

39. A. G. Ghani, M. M. Farid, X. D. Chen, P. Richards. “Numerical simulation of natural convection heating of canned food by computational fluid dynamics”. Journal of Food Engineering. Vol. 41. 1999. pp. 55-64.        [ Links ]

40. W. H. Yang, M. A. Rao. “Transient natural convection heat transfer to starch dispersion in a cylindrical container: Numerical solution and experiment”. Journal of Food Engineering, Vol. 36. 1998. pp. 395-415.        [ Links ]

41. A. K. Datta, A. A. Teixeira. “Numerical modeling of natural convection heating in canned liquids foods”. Transactions of the American Society of Agricultural Engineers. 1987. Vol. 30. pp. 1552-1561.        [ Links ]

42. A. K. Datta, A. A. Teixeira. “Numerically predicted transient temperature and velocity profiles during natural convection heating of canned liquid foods”. J.of Food Science. Vol. 53. 1988. pp. 191-195.        [ Links ]

43. A. Kumar, M. Bhattacharya. “Transient temperatura and velocity profiles in a canned non-newtonian liquid food during sterilization in a still-cook retort”. International Journal of Heat and Mass Transfer. Vol. 34. 1991. pp. 1083-1096.        [ Links ]

44. A. G. Ghani, M. F. Mohammed, X. D. Chen. “A CFD simulation of the coldest point during sterilization of canned food”. The 26^th Australian Chemical Engineering Conference. 28-30 September 1998. Port Douglas. Queensland. Paper 358 on CD-ROM (ISBN 1 85825 6835).        [ Links ]

45. A. G Ghani, M. M. Farid, X. D Chen, P. Richards. “An investigation of deactivation of bacteria in canned liquid food during sterilization using computational fluid dynamics”. (CFD) Journal of Food Engineering. Vol. 42. 1999. pp. 207-214.        [ Links ]

46. S. Siriwattanayotin, T. Yoovidhya, T. Meepadung, W. Ruenglertpanyakul. “Simulation of sterilization of canned liquid food using sucrose degradation as an indicator”. Journal of Food Engineering. Vol. 73. 2006. pp. 307-312.        [ Links ]

47. A. G. Ghani, M. M. Farid, X. D. Chen. “Numerical simulation of transient temperature and velocity profiles in a horizontal can during sterilization using computational fluid dynamics”. Journal of Food Engineering. Vol. 51. 2002. pp. 77-83.        [ Links ]

48. M. N. Varma, A. Kannan. “Enhanced food sterilization through inclination of the container walls and geometry modifications”. International journal of heat and mass transfer. Vol. 48. 2005. pp. 3753-3762.        [ Links ]

49. Y. Choi, M. Okos. “Effects of temperature and composition on thermal properties of foods. Food engineering and process applications. Vol. 1”. Maguer, P. Jelens (Eds). Transport Phenomenon. L. Elsevier. New York. 1986. pp. 93-101.        [ Links ]

50. J. M. Alvarado Orozco, J. L. Navarrete Bolaños, J. E. Botello Álvarez, G. M. Martínez, H. Jiménez Islas. “Efecto de la viscosidad sobre la convección natural 2-D en cavidades cilíndricas, durante la esterilización de alimentos líquidos”. Memorias del XXIX EncuentroNacional de la AMIDIQ. Puerto Vallarta. Jalisco. 2008. Vol 4. pp. 162-172.        [ Links ]

51. L. J. Wang, D. W. Sun. “Recent developments in numerical modelling of heating and cooling processes in the food industry - a review”. Trends in Food Science & Technology. Vol. 14. 2003. pp. 408-423.        [ Links ]

52. X. D. Chen, H. J. Huang, A. G. Ghani. “Thermal sterilization of liquid foods in sealed containerdeveloping simple correlations to account for natural convection”. International Journal of Food Engineering. Vol. 1. 2005. pp. 1-23.        [ Links ]

(Recibido el 17 de diciembre de 2008. Aceptado el 24 de agosto de 2009)

^*Autor de correspondencia: teléfono: + 52 + 461 + 611 75 75, Ext. 323, correo electrónico: hugo@itc.mx (H. Jiménez).