Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.62 Medellín Jan./Mar. 2012
ARTÍCULO ORIGINAL
An enhanced vector diagram of Maxwell's equations for chiral media
Un diagrama vectorial mejorado, de las ecuaciones de Maxwell, para medio quiral
Carlos Villarroel González1*, Diego Torres Cabezas2, Héctor Torres Silva1
1Escuela Universitaria de Ingeniería Eléctrica-Electrónica. Universidad de Tarapacá. Avda. 18 de Septiembre 2222, Casilla Postal 6-D. Arica, Chile.
2Modernización y Gobierno Electrónico. Ministerio Secretaría General de la Presidencia. Gobierno de Chile. Teatinos 333, Piso 4°. C. P. 8340382 Santiago, Chile.
*Autor de correspondencia: teléfono: + 58 + 56 + 205144, fax: + 58 + 56 + 232350, correo electrónico: carlosvillaroel@uta.cl (F. González)
(Recibido el 28 de enero de 2011. Aceptado el 28 de febrero de 2012)
Abstract
A vector diagram of Maxwell’s time-harmonic equations in homogeneous isotropic media is derived and proposed so as to include chiral media. The diagram may be used to obtain a number of common relationships between fields, potentials and source by equating appropriate components of the vectors in it. The construction of the diagram is based on the formal similarity between many theorems of vector calculus and those of vector algebra. Construction of the diagrams for two different gauge choices, Lorentz and Coulomb’s gauges, is explained in detail and some of equations which can possibly be derived from one of the diagram are presented. In this work this approach is applied to a numerical calculation of a two-dimensional chiral slab. This work could be a tool for designing Wireless Communications Systems devices, in a spectral range from 1 GHz to about 60 GHz, for example, duplexers based on power splitters and a rear frequency selective filtering though the use of SRR/ CSRR (splits ring resonator)/ (coplanar SRR) cells. The circuit devices using SRR/CSRR have a very small size, due to its operations in a sub-lambda system. Also this work may be useful to discuss the design, among others, of a circularly polarized printed patch for S- Band and different types of filters and others devices using metamaterials and Coplanar Wave Guides.
Keywords: Chiral media, Maxwell's equation, vector diagram, wireless communications devices
Resumen
En este trabajo se deriva un diagrama de las ecuaciones de Maxwell, en medios homogéneos isotrópicos, tal que pueda incluir un medio quiral. Este diagrama puede ser utilizado para obtener las relaciones entre campos, potenciales y fuentes, relacionando en forma adecuada las componentes vectoriales presentes en el diagrama. La construcción de este diagrama está basada en la similitud formal entre muchos teoremas del cálculo vectorial y aquellos del algebra vectorial. Se explica, en detalle, la construcción del diagrama para dos diferentes calibres, el de Lorentz y el de Coulomb, y se presentan algunas ecuaciones que pueden ser obtenidas del diagrama. En este trabajo, este enfoque, se aplica al cálculo numérico bidimensional de dos láminas quiral. Este trabajo puede ser una herramienta posible de usar en el diseño de dispositivos utilizados en sistemas de comunicaciones inalámbricas, en el rango espectral desde 1 GHz hasta aproximadamente 60 GHz, por ejemplo duplexores basados en divisores de potencia y filtraje posterior de frecuencia, utilizando SRR/CSRR (resonador de anillos divisores)/ celdas coplanares SSR. Los dispositivos de circuito que utilizan SRR/CSRR tienen un tamaño muy pequeño, debido a que operan en sistemas sub-lambda. Este trabajo también puede ser útil para el análisis del diseño, entre otros, de parches impresos para la banda S y para la discusión de diferentes tipos de filtros y otros dispositivos que utilicen metamateriales y guías de onda coplanares.
Palabras clave: Medio quiral, ecuaciones de Maxwell, dispositivos de comunicaciones inalámbricas
Introduction
Many modern satellite and terrestrial point to point communication systems use circular polarization (CP) wave polarization in order to maximize the polarization efficiency component of the link budget. The channel capacity of a communications link can be doubled in a polarization diversity system achieved by the simultaneous generation of orthogonal linear field components. For many communication systems especially in the case for satellite and ground station antennas, operation in circular polarization mode is preferred , since it removes the need to continuously align the two apertures, which otherwise would be required to maximize the receiver power. In addition, CP signals are not subject to the Faraday rotation effect, which causes the linear field vectors to rotate as a consequence of interaction with static magnetic fields along the propagation path [1]. The theory exposed here can be adequate to study this problem.
Design of dual and circular polarization microstrip antennas demands precise control of the individual radiated polarizations. Circular Polarization can be obtained when the two orthogonal modes are excited with equal power signals and in phase quadrature (90° out of phase at the center frequency). These modes may be excited in a number of ways, for example, the excitation can be done through reactive splitters (using difference in line lengths), isolating splitters (such as branch line, Wilkinson, hybrid ring) or degenerate mode single feed. In this single feed patch, its asymmetry excites the orthogonal modes. It is found that the performance is very similar to the reactive splitter fed patch with the axial ratio degrading with frequency away from resonance, while the input matching remains acceptable [2].
Also, using a single frequency [a continuous laser beam] it should be possible to produce a pure curl state by focusing at 90° a circularly polarized Gaussian beam [3]. Unfortunately, today commercial objectives permit one to focus a beam at no more than 70°-80°. However, inputs can come from spatial light modulators or metamaterials. For a pulsed laser, things are more challenging because a very large light spectrum is needed — we are speaking of a pulse of a few attoseconds; however, it may still be feasible.
Since knotted light beams have both beamlike properties and unique unexplored properties, they may find applications in many different fields. These could include applications in plasma confinement, atomic particle trapping, manipulating cold atomic ensembles, and generating soliton-like solutions in nonlinear media. ''In trapping colloidal particles, for example, there is a growing interest in exploring the possibilities that arise when the full three- dimensional structure of focused beams is considered. ''In particular, there is interest in the possibility of the optical force having a nonconservative component, which arises when the curl of the field of force exerted on the particle by the light is non-zero. While not force-field curl eigenstates, the building block of the beams we consider have electric and magnetic fields that are curl-eigenstates. It would be interesting to carry this structure over to the force-field. Another potential, though at this stage speculative application lies in plasma physics''. These problems may be studied with our approach when the Maxwell's equations give a Beltrami equation when the electric field is parallel to the magnetic field.
The idea of having knots in light as such is very exciting and could lead to many applications - maybe it is still too early to say exactly what kind of applications. Someday, if we were able to effectively create and manipulate knots of light, maybe we could speculate that there could also be a way to store and transform information in this way. Maybe we could develop some very fast computer memory or use them in cryptography for sending encrypted information. Too early to say, but the possibilities are definitely there.
The idea of representing Maxwell’s time-harmonic equations in homogeneous isotropic media by vector diagram as put forward by Wilton [4] and by S. Uckun [5] deserves consideration. All the common relations between field and potential quantities implied by Maxwell’s equations are represented by a diagram. It is started that the diagram not only illustrates Maxwell’s equations, but also many of the methods for constructing diagram are based on the formal similarity between many theorems of vector calculus and those of vector algebra.
An isotropic chiral medium is a macroscopically continuous medium composed of equivalent chiral objects that are uniformly distributed and randomly oriented. A chiral object is a three- dimensional body that cannot be brought into agreement with its mirror image by translation and rotation. An object of this sort has the property of handedness and must be either left-handed or right-handed. An object that is not chiral is said to be achiral, and thus all objects are either chiral o achiral. Due to their novel properties and wide applications in microwave and radar engineering, chiral media has been undergoing extensive research during the last years. That is why this study aims to cover chiral medium for the representation of Maxwell’s equations in vector diagram form. In a chiral media a cross coupling between electric and magnetic filed exists. Thus, the vector diagram has vectors along all three coordinate axes where as the vector diagram presented by Wilton [3] for achiral media has vectors only in one plane with H vector normal to it.
Vector diagram construction
Assuming ejωt time dependence, Maxwell’s time-harmonic equations [5, 6] for isotropic, homogeneous, linear media are:

Chirality is introduced into the theory by defining the following constitutive relations to describe the isotropic chiral medium [5]

Where the chirality admittance -ωεT indicates the degree of chirality of the medium, and the ε and µ are permittivity and permeability of the chiral medium, respectively. Since D and E are polar vectors and B and H are axial vectors, it follows that ε and µ are true scalars and -ωεT is a pseudoscalar. This means that when the axes of a right-handed Cartesian coordinate system are reversed to form a left-handed Cartesian coordinate system, -ωεT changes in sign whereas ε and µ remain unchanged.
For a graphical representation of the above relationships, following Wilton’s procedure [3], let us assume vector-differential operator,  is an ordinary vector and treat the divergence and curl operations in equations to as ordinary scalar (dot) and vector (cross) products, respectively. Equation implies that
is an ordinary vector and treat the divergence and curl operations in equations to as ordinary scalar (dot) and vector (cross) products, respectively. Equation implies that  is perpendicular to B and the vector
is perpendicular to B and the vector  xB must be perpendicular to both
xB must be perpendicular to both  and B.
and B.
As shown in figure 1, three transverse coordinate axes are chosen as  , from equation (1)B = -
, from equation (1)B = - x E/(jω) and,
x E/(jω) and,  x B/(jωεµ) =
x B/(jωεµ) =  x
x  x E/k2 where k2 = ω2.εµ
x E/k2 where k2 = ω2.εµ
Since  B = 0 always, this conditions will hold identically if B is expressed as the curl of a vector potential A since the divergence of the curl of a vector is identically zero. Thus
B = 0 always, this conditions will hold identically if B is expressed as the curl of a vector potential A since the divergence of the curl of a vector is identically zero. Thus

and A must be perpendicular to both  and B and lie in
and B and lie in  and
and  x B plane. However, A is not unique since only its components perpendicular to
x B plane. However, A is not unique since only its components perpendicular to  contribute to the cross product. Therefore,
contribute to the cross product. Therefore,  .A, the component of A parallel to
.A, the component of A parallel to  , must be specified. The curl equation for E, as in equation (1), and equation (7) give
, must be specified. The curl equation for E, as in equation (1), and equation (7) give  x (E +jωA) = 0 where the quantity in parentheses should be parallel to
x (E +jωA) = 0 where the quantity in parentheses should be parallel to  and the curl of the gradient of a scalar function Φ is identically zero; so the general integral of the above equation is E + jωA = -
and the curl of the gradient of a scalar function Φ is identically zero; so the general integral of the above equation is E + jωA = - ϕ or
ϕ or

As shown in figure 1.
Following the Uckun’s approach [5], we substitute equation (7) into equation (6) having

Substituting equation (9) and equation (5) into equation (2) gives  placing the value of
placing the value of  xE from equation into the above equation
xE from equation into the above equation 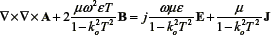 using the vector identity
using the vector identity  x
x xA =
xA =  (
( .A) -
.A) -  2A enables us to write the above equation as
2A enables us to write the above equation as  and using equation (8)
and using equation (8)

Here  .A is arbitrary, so in order to specify
.A is arbitrary, so in order to specify  .A, for unique A, we may choose
.A, for unique A, we may choose

And eliminate the term in parentheses. The choice in equation (11) is known as Lorentz gauge. Then equation (10) will be simplified to

Divide both sides of equation (12) by  and reorganize it to get
and reorganize it to get

See figure 1.
The difference between our approach and the Uckun’s procedure [5], is that we take the chiral media characterized by D = ε(E + β x E) and B = µ(H + β
x E) and B = µ(H + β xH). In this form we can obtain the spatial parallel condition between B and E where the main equation is like a Beltrami equation which is important for the numerical simulation.
xH). In this form we can obtain the spatial parallel condition between B and E where the main equation is like a Beltrami equation which is important for the numerical simulation.
Placing the value of B from equation (1) into equation (5) D = ε(E + β xE) will be obtained. Placing the value of H, from equation (6), and D into equation (2) will give
xE) will be obtained. Placing the value of H, from equation (6), and D into equation (2) will give  by rearranging this equation
by rearranging this equation

will be obtained as shown in figure 1. In this figure we put µ  µ(1 - k02T2). Taking divergence of equation (5) and using equations (3) and (4) in it
µ(1 - k02T2). Taking divergence of equation (5) and using equations (3) and (4) in it

Will be derived. To find the projection of E onto  , from equation (15)
, from equation (15)  .E = ρ / ε, take the gradient of both sides and divide by scalar value
.E = ρ / ε, take the gradient of both sides and divide by scalar value  2 to normalize
2 to normalize  to a unit vector. So
to a unit vector. So

Similarly, getting gradient of both sides of equation (11), using the vector identify  x
x xA+
xA+ 2A for
2A for  (
( .A) and normalizing by
.A) and normalizing by  2
2

will be obtained as parallel component of A to  coordinate.
coordinate.
By using equations (8), (13), (14), (16) and (17), the vector diagram of Lorenz gauge can be completed as shown in figure 1, where all Maxwell’s relations and potential quantities appear.
Now let us examine derivation of some relations from the diagram. For example, it is seen that the component of E and J/(jωε) parallel to  must be equal and apposite. By taking the divergence of equation (14) and using
must be equal and apposite. By taking the divergence of equation (14) and using  .E = ρ/ε can be shown that
.E = ρ/ε can be shown that

Taking the gradient in both sides of equation (18) and dividing it by scalar value  2 will given the same value as equation (16) with opposite sign. From the right side of equation (18) it is seen that
2 will given the same value as equation (16) with opposite sign. From the right side of equation (18) it is seen that

This is the known continuity equation. Since the divergence of the curl of any vector is identically zero, the divergence of equation (2) yields 0 = jω .D +
.D +  .J. Using equiation (4) convert this immediately into continuity equation as, expected. Again, as seen in figure 1, 2β
.J. Using equiation (4) convert this immediately into continuity equation as, expected. Again, as seen in figure 1, 2β xE and -jω2β
xE and -jω2β xA are equal and opposite vectors. From equation (8), taking curl of both side and using the vector identity
xA are equal and opposite vectors. From equation (8), taking curl of both side and using the vector identity  x
x ϕ = 0 will show that
ϕ = 0 will show that

as expected. By using the vector calculus a few possible equations from the vector diagram can be written as follows

For example, adding equations (13) and (14) side by side and using equation (8) will give equation (24) which shows the correctness of the equation derived from the diagram 1. Instead of Lorenz gauge we can choose Coulomb’s gauge.

In equation (10) so that it will take the form  where the subscript ''c'' is used it indicate Coulomb’s gauge. Using equation (8) and (20) in the above equation
where the subscript ''c'' is used it indicate Coulomb’s gauge. Using equation (8) and (20) in the above equation

will be obtained. Placing the values of equations (5) and (6) into equation (2) will give  and value of
and value of  xE from equation will give
xE from equation will give 
Combining these equations with equation (26) and using equation (7) we have

By using the same coordinates axes  , B and (1 – k02T2)
, B and (1 – k02T2) xB/(jωµε) and equation (1), (8), (16), (26) and (27) for the Coulomb gauge. It is clear from equation that the component of the vector A parallel to
xB/(jωµε) and equation (1), (8), (16), (26) and (27) for the Coulomb gauge. It is clear from equation that the component of the vector A parallel to  is equal to zero.
is equal to zero.
As seen in figure 1, Lorenz gauge are the best choice because these make A either parallel or perpendicular to any of the other vectors and simplify its relationship to those vectors. In figure 1 if the chirality constant T, goes to zero, point K, L and R approach point M. P, and N respectively, in which case the diagram will be the same as in Reference [7] for linear, homogeneous, isotropic achiral medium. If (1 – k02T2)  0 then E is parallel to B, and parallel to A so all vectors remain in an only plane. This Beltrami condition is usefull to numerical calculations. We apply this approach to a two dimensional chiral slab.
0 then E is parallel to B, and parallel to A so all vectors remain in an only plane. This Beltrami condition is usefull to numerical calculations. We apply this approach to a two dimensional chiral slab.
This result cannot be obtained with the Uckun's approach [5].
Two dimension chiral slab
Considering a two dimension chiral slab with material polariton, where a polariton is the result of the mixing of a photon with an excitation of a material in figures 2 and 3 with the aid of figure 1, the spatial variation of the magnetic and electric field amplitudes versus y is sketched for an incident TE plane wave whose electric field is given by  , with a transverse wave-number equal to the TE material polariton one kt = 5.28x10-3k0 and k0T = 0.3. The complete coupling between the plane wave and the cover polariton assures that the reflected field from the slab (and possibly the corresponding enhancement on the screen) has its maximum and that the total field is entirely dominated by the material polariton distribution, as evident from figures 2 and 3 where the field complex amplitudes have only real or imaginary parts.
, with a transverse wave-number equal to the TE material polariton one kt = 5.28x10-3k0 and k0T = 0.3. The complete coupling between the plane wave and the cover polariton assures that the reflected field from the slab (and possibly the corresponding enhancement on the screen) has its maximum and that the total field is entirely dominated by the material polariton distribution, as evident from figures 2 and 3 where the field complex amplitudes have only real or imaginary parts.
The slab has the same parameters ε = ε0, µ=10-3µ0, dsalb=4/k0, kt =(4.46 +j4.51x10-3)k0 and kt = (5.28 x 10-3)k0 respectively for the leaky wave and the material polariton supported by the grounded slab.
The slab has the same parameters of figure 2.
The two plots clearly show how the material polariton of such a structure behaves in this case: The electric field inside the slab assumes values comparable with outside (i.e., twice the value of the incident field, due to the total reflection from the screen), whereas the magnetic field builds up on the screen, consistently with the theory. If the plane wave had impinged at a different angle without noticeably exciting the polariton, we would have expected a much lower value for the electric field inside the slab (due to the low intrinsic impedance η of the chosen metamaterial) and a value of the magnetic field comparable with outside. Not surprisingly, such an excitation would not cause any enhancement in the transmission properties [8].
Also, at optical level, our approach can to show how a new class of knotted beams of light can be derived, where approximate knots of light may be generated using tightly focused circularly polarized laser beams. We predict theoretical extensions and potential applications, in fields ranging from fluid dynamics, topological optical solitons and particle trapping to cold atomic gases and plasma confinement [9-11].
Conclusion
Vector diagrams of Maxwell’s time-harmonic equations in homogeneous isotropic chiral media have been derived for Lorenz and Coulomb gauges separately. The diagrams illustrated Maxwell’s equations, relationship among the vector and scalar potential and field quantities and standard relationships derivable from them. A number of formulas may be derived simply by equating various vector components in the diagram. Since we are working with three dimensional vector diagrams, the numbers of possible derivable formulas are greater than in the case examined by Wilton [4] and Uckun [5]. With our approach we are able to obtain the parallel condition between the electric field and magnetic field. A chiral slab is studied with this approach. This approach is a powerful tool for low cost and reduced size implementations in high-frequency planar technology and optical vortex situations.
References
1. R. Shimano, H. Nishimura, T. Sato. ''Frequency Tunable Circular Polarization Control of Terahertz Radiation.'' Jpn. J. Appl. Phys. Vol. 44. 2005. pp. L676-L678. [ Links ]
2. E. Castro, J. Lloyd, M. Johnston, M. Fraser, H. Tan, C. Jagadish. ''Polarization-sensitive terahertz detection by multicontact photoconductive receivers''. Appl. Phys. Lett. Vol. 86. 2005. pp. 254102-254102-3. [ Links ]
3. W. Irvine, D. Bouwmeester. ''Linked and knotted beams of light''. Nature Physics. Vol. 4. 2008. pp. 716-720. [ Links ]
4. D. Wilton. ''A Vector Diagram of Maxwell's Equations''. IEEE Antennas and Propagation Magazine. Vol. 37. 1995. pp. 7-11. [ Links ]
5. S. Uckun. A Vector Diagram of Maxwell's Equations for chiral media. Electrotechnical Conference. Melecon 98. 1998. pp. 283-286. [ Links ]
6. H. Torres, M. Zamorano. ''Chiral Effect on Optical Soliton''. The journal mathematics and Computers in Simulation. Vol. 62. 2003. pp. 149-161. [ Links ]
7. H. Torres, C. Villarroel, F. Jiménez. ''Electromagnetic waves at the plane boundary between two chiral media''. Ingeniare. Revista chilena de ingeniería. Vol. 15. 2007. pp. 101-110. [ Links ]
8. A. Alu, N Engheta. ''Pairing an epsilon- negative slab with a mu negative: Resonance, Anomalous Tunelling and Transparency''. IEEE Transaction. Vol. 51. 2003. pp. 2558-2571. [ Links ]
9. I. Bialynicki-Birula, Z. Bialynicka-Birula. ''Vortex lines of the electromagnetic field''. Phys. Rev. A. Vol. 67. 2003. pp. 062114-062114-8. [ Links ]
10. M. Berry, M. Dennis. ''Knotted and linked phase singularities in monochromatic waves.'' Proc. R. Soc. Lond. A. Vol. 457. 2001. pp. 2251-2263. [ Links ]
11. J. Leach, M. Dennis, J. Courtial, M. Padgett. ''Knotted threads of darkness''. Nature. Vol. 432. 2004. pp. 165-166. [ Links ]

















