Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.63 Medellín Apr./June 2012
ARTÍCULO ORIGINAL
Un método híbrido de optimización para el Planeamiento de la transmisión considerando diferentes niveles de tensión
A hybrid optimization method for the transmission planning considering different voltage levels
Andrés Hernando Domínguez1, Antonio Escobar Zuluaga2, Ramón A. Gallego R.3
1Grupo De Investigación Planeamiento En Sistemas Eléctricos. Programa Ingeniería Eléctrica. Universidad Tecnológica de Pereira. A.A 97. Pereira, Colombia.
2Profesor en Programa Tecnología Eléctrica. Universidad Tecnológica de Pereira. A.A 97. Pereira, Colombia.
3Profesor en Programa Ingeniería Eléctrica. Universidad Tecnológica de Pereira. A.A 97. Pereira, Colombia.
*Autor de correspondencia: teléfono: + 57 + 6 + 313 71 22 ext. 122, fax: + 57 + 6 + 313 71 22 ext. 116, correo electrónico: andreshdomin-guez@gmail.com (A. Domínguez)
(Recibido el 29 de febrero de 2012. Aceptado el 7 de junio de 2012)
Resumen
En este artículo se presenta una propuesta de solución para resolver el problema de planeamiento de la expansión de redes de transmisión de energía eléctrica, considerando el nivel de tensión de las líneas como una variable. Considerar el cambio de nivel de tensión permite beneficiarse de las economías de escala que aparecen cuando un circuito cambia de un nivel de tensión preestablecido a un nivel de tensión mayor. Definir a priori la tensión de los nuevos corredores es menos efectivo que considerar la tensión como una de las cantidades que deben ser definidas por el proceso de evaluación de alternativas. Se propone una metodología híbrida para resolver el problema resultante, el cual presenta un aumento exponencial de posibilidades que surgen al considerar distintos niveles de tensión y diferentes alternativas de inversión. En esta propuesta, una técnica metaheurística determina las inversiones que deben realizarse en líneas de transmisión, mientras que procedimientos heurísticos combinados con un microgenético determinan las inversiones en subestaciones nuevas y existentes. Los resultados muestran un muy buen desempeño de la metodología implementada.
Palabras clave: Algoritmo genético, codificación, heurísticas, nivel de tensión, optimización, planeamiento de la transmisión
Abstract
In this article an alternative to solve the transmission network expansion planning problem taking the voltage level as a decision variable is presented. The idea is to benefit from the scale economies which appear when a circuit changes from a preestablished tension level to a higher tension level. Predefine the tension of the new circuits is less effective than taking the tension as one of the quantities that must be defined for the process of alternative's evaluation. It is proposed a hybrid methodology to reduce the computational effort produced by the exponential growth caused for considering different voltage levels and investment alternatives. In this work, the meta-heuristic technique specifies where should be done the transmission line investments, meanwhile the heuristic techniques and the micro-genetic algorithm specifies the investment in new and existing substations. The developed methodology presented high-quality results.
Keywords: Genetic algorithm, codification, heuristics, voltage level, optimization, transmission planning
Introducción
El problema tradicional de planeamiento de la expansión de la transmisión, denominado planeamiento estático, consiste en determinar la inversión de mínimo costo que debe ser realizada en un sistema de potencia, para satisfacer los requerimientos futuros de demanda y generación del sistema. En la inversión se considera la adición de nuevas subestaciones, la adición de nuevos transformadores en subestaciones existentes y la construcción de nuevas líneas de transmisión. El problema de planeamiento se caracteriza por tener variables de decisión enteras, variables de operación continuas y por incluir restricciones no lineales. En sistemas de gran tamaño, el problema de planeamiento se clasifica en el grupo de los problemas no lineales entero-mixtos (PNL-EM) de difícil solución o NP-completos. Estos presentan múltiples óptimos locales y el denominado fenómeno de explosión combinatorial. En la literatura especializada existen diversas propuestas para solucionar el problema de planeamiento las cuales usan técnicas exactas, técnicas heurísticas y técnicas metaheurísticas. La referencia [1] muestra los modelos y las técnicas más utilizadas para resolver este problema. Las técnicas exactas son eficientes en problemas de pequeño y mediano tamaño. En los sistemas de gran tamaño y complejidad normalmente estas técnicas no consiguen encontrar la solución del problema. Por otro lado, las técnicas metaheurísticas han mostrado ser muy eficientes cuando resuelven problemas del tipo NP-completo, y en particular, han mostrado un gran desempeño en el área de planeamiento eléctrico encontrando soluciones de alta calidad [2, 3]. En el problema de planeamiento de la expansión tradicional, un agente planeador selecciona las localizaciones de las subestaciones futuras y establece los niveles de tensión de los corredores nuevos. Se asume que esta información de entrada ha sido adecuadamente definida. Con la metodología propuesta en este trabajo, no se requiere definir la localización de nuevas subestaciones ni los niveles de tensión de los corredores nuevos, ya que el proceso de optimización maneja una base de datos aumentada virtualmente que considera implícitamente la posibilidad de ubicar nuevas subestaciones en nodos donde no existen y que el sistema está necesitando. Este manejo de información permite mayor flexibilidad respecto al planeamiento tradicional. También permite predecir requerimientos del sistema, no previstos por el agente planeador, y guiar las decisiones futuras asociadas a nuevos niveles de tensión que el sistema aún no posee.
En el problema de planeamiento tradicional, el conjunto de variables de decisión representa las adiciones en líneas de transmisión y en transformadores de subestaciones nuevas o existentes. Las técnicas de solución tradicionales no hacen una diferenciación entre estos tipos de variables. En este trabajo se propone separar las variables con el objetivo de definir reglas diferentes para líneas y subestaciones. Esta forma de resolver el problema permite aprovechar las particularidades de los dos tipos de variables y mejorar la eficiencia computacional.
En este trabajo, un algoritmo genético de Chu-Beasley (AGCB) selecciona los mejores subconjuntos de adiciones en líneas de transmisión, y procedimientos heurísticos determinan la capacidad de las subestaciones para cada propuesta de inversión. De esta forma, el AGCB trabaja sobre un vector de variables de decisión de menor tamaño que el que tendría si tuviera que decidir también respecto a las inversiones en subestaciones. El vector de variables de inversión en líneas difiere del que se usa normalmente en planeamiento ya que debe incluir una variable para decidir el número de circuitos en cada corredor de transmisión y otra variable para determinar su nivel de tensión. En la literatura especializada es muy incipiente aún el número y la calidad de los trabajos que incluyen como variable el nivel de tensión de los corredores. En [4] se presenta una propuesta para el planeamiento considerando el nivel de tensión. Sin embargo no se considera el efecto eléctrico de los transformadores de la red, lo que ocasiona resultados diferentes a los que aparecen cuando se considera la reactancia, como se muestra en [5].
En general la metodología implementada pretende potenciar la búsqueda en el espacio de solución aprovechando la separación de las inversiones en líneas de transmisión de las inversiones en subestaciones, y de la combinación de técnicas heurísticas y metaheurísticas. Las alternativas implementadas para la evaluación de las capacidades de las subestaciones usan factores de sensibilidad o una búsqueda local realizada con un microgenético. De esta forma, se determina heurísticamente el número, ubicación y el costo de los transformadores. Es importante aclarar que en esta propuesta sólo se consideran explícitamente las subestaciones existentes, es decir, se conservan los números de los nodos de la red original entre los que existan transformadores. Las subestaciones nuevas sólo aparecen si el sistema las requiere.
Modelo del problema de planeamiento
A continuación se presenta el modelo matemático usado para resolver el problema de planeamiento estático de la transmisión basado en cambio de nivel de tensión. Este último se deriva del modelo DC [6], el cual es considerado ideal cuando se hacen trabajos de planeamiento de la transmisión.

En este modelo, cij es el costo de adicionar una línea en la rama i-j en la red base, c’ij,t es el costo de adicionar una línea en la rama i-j en la red nueva de nivel de tensión t, Ω2 y Ω3 representan el conjunto de los corredores de transmisión existentes en la red base y corredores de transmisión nuevos, Ω1 es el conjunto de nodos con carga, α es un parámetro de penalización asociado a la potencia no servida, r es el vector de generadores artificiales, S0 y S' son matrices de incidencia nodo-rama del sistema eléctrico en la red base y red nueva, f0 y f' son vectores de flujo cuyos elementos representan el flujo total en el camino i-j en la red base (fi0j) y red nueva (f'ij)y para la red nueva en el nivel de tensión t, g es el vector de generaciones nodales, d es el vector de demandas nodales, γij y γ'ij,t. son la susceptancia de una línea en el corredor i-j en la red base y en la red nueva en el nivel de tensión t, θ es el vector de ángulos nodales,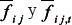 son el flujo máximo permitido para una línea en el camino i-j en la red base y red nueva, y para la red nueva en el nivel de tensión t,
son el flujo máximo permitido para una línea en el camino i-j en la red base y red nueva, y para la red nueva en el nivel de tensión t,  es el vector de máxima generación nodal, nij es el número de refuerzos adicionados en la rama i-j en la red base,
es el vector de máxima generación nodal, nij es el número de refuerzos adicionados en la rama i-j en la red base, 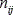 es el número máximo de líneas que se pueden adicionar en la rama i-j, n0ij es el número de líneas en la rama i-j en la red base, n'i j,t es el número de líneas adicionadas en la rama i-j en el nivel de tensión t, y Yij,t es una variable binaria para elegir el nivel de tensión. La función objetivo está compuesta por tres términos: el primero representa la suma de los costos de los refuerzos adicionados en la red base, el segundo representa la suma de los costos de los elementos adicionados en el nivel de tensión t en la red nueva y el tercero representa la suma de demandas no atendidas en los nodos de carga. En el modelo se deben hacer las siguientes aclaraciones: 1) M, es un parámetro que se define a priori de gran tamaño, para establecer un control en la segunda ley de Kirchhoff para los límites de la abertura angular. 2) El grupo de restricciones f'ij,t-(θi-θt)n'i j,t γ'ij,t Yi j,t= 0 , representan la segunda ley de Kirchhoff aplicada al conjunto de reactancias de cada corredor de transmisión nuevo, conectada entre los nodos i-j al nivel de tensión t. Si el nivel de tensión t está seleccionado, el valor de Yi j,t= 1, y se aplica la segunda ley de Kirchhoff al corredor. Si Yi j,t= 0 no se aplica la segunda ley de Kirchhoff a dicho corredor y, adicionalmente, obliga a que el flujo f'ij,t sea cero. 3) La restricción
es el número máximo de líneas que se pueden adicionar en la rama i-j, n0ij es el número de líneas en la rama i-j en la red base, n'i j,t es el número de líneas adicionadas en la rama i-j en el nivel de tensión t, y Yij,t es una variable binaria para elegir el nivel de tensión. La función objetivo está compuesta por tres términos: el primero representa la suma de los costos de los refuerzos adicionados en la red base, el segundo representa la suma de los costos de los elementos adicionados en el nivel de tensión t en la red nueva y el tercero representa la suma de demandas no atendidas en los nodos de carga. En el modelo se deben hacer las siguientes aclaraciones: 1) M, es un parámetro que se define a priori de gran tamaño, para establecer un control en la segunda ley de Kirchhoff para los límites de la abertura angular. 2) El grupo de restricciones f'ij,t-(θi-θt)n'i j,t γ'ij,t Yi j,t= 0 , representan la segunda ley de Kirchhoff aplicada al conjunto de reactancias de cada corredor de transmisión nuevo, conectada entre los nodos i-j al nivel de tensión t. Si el nivel de tensión t está seleccionado, el valor de Yi j,t= 1, y se aplica la segunda ley de Kirchhoff al corredor. Si Yi j,t= 0 no se aplica la segunda ley de Kirchhoff a dicho corredor y, adicionalmente, obliga a que el flujo f'ij,t sea cero. 3) La restricción 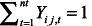 garantiza que por cada corredor de transmisión nuevo i-j, sólo pueda seleccionarse un nivel de tensión t del subconjunto de nt niveles posibles. 4) Existen dos restricciones de abertura angular, la primera es aplicada a los corredores de la red existente, y en la segunda, el término M(1 – Yij,nt) se hace cero para el corredor i-j al nivel de tensión seleccionado para dicho corredor (Yij,tk = 1), convirtiendo la restricción en:
garantiza que por cada corredor de transmisión nuevo i-j, sólo pueda seleccionarse un nivel de tensión t del subconjunto de nt niveles posibles. 4) Existen dos restricciones de abertura angular, la primera es aplicada a los corredores de la red existente, y en la segunda, el término M(1 – Yij,nt) se hace cero para el corredor i-j al nivel de tensión seleccionado para dicho corredor (Yij,tk = 1), convirtiendo la restricción en: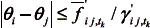 , ya que los demás términos asumen valores muy grandes porque para ellos Yij,tk = 0, y la función usada selecciona el menor valor. 5) El modelo (1) permite adiciones sobre los corredores de transmisión existentes en la red inicial pero conserva el nivel de tensión de dichos corredores.
, ya que los demás términos asumen valores muy grandes porque para ellos Yij,tk = 0, y la función usada selecciona el menor valor. 5) El modelo (1) permite adiciones sobre los corredores de transmisión existentes en la red inicial pero conserva el nivel de tensión de dichos corredores.
Metodología de solución
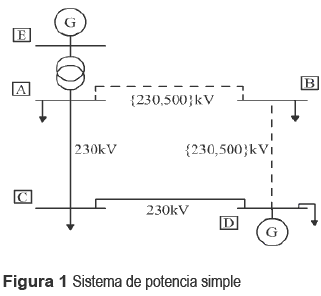
El sistema de potencia de la figura 1 permite mostrar el procedimiento que se sigue al resolver el problema de planeamiento aplicando la metodología propuesta
En este sistema, los circuitos existentes en la red actual se representan con trazos continuos mientras que los corredores de transmisión futuros, asociados exclusivamente a líneas de transmisión candidatas, se representan con trazos interrumpidos. Se puede observar que existen circuitos de 230KV conectando los nodos A y C, y los nodos C y D. Estos circuitos, al igual que sus tensiones, se conservan en el proceso de expansión ya que no considera modificar el nivel de tensión de los circuitos existentes. De otro lado, el nodo B es un nodo futuro y, por lo tanto, no se encuentra conectado aún al sistema. De acuerdo con la figura 1, este nodo nuevo puede conectarse a la red existente a través de dos corredores nuevos: el corredor A-B y el corredor B-D. Una propuesta de inversión puede usar solo uno de los corredores o utilizar ambos corredores y está por definirse el número de circuitos por corredor y su tensión. En el ejemplo de la figura 1 los corredores nuevos tienen asociadas dos alternativas de tensión: 230KV ó 500KV.
La técnica metaheurística (AGCB) sólo considera inversiones en líneas de transmisión únicamente. Entre las propuestas del AGCB pueden aparecer casos donde el corredorAB y el corredor BD tengan niveles de tensión diferentes. Por ejemplo, puede aparecer una propuesta con AB a 230KV y BD a 500KV. En estos casos, la metodología determina que es necesario adicionar una subestación 230KV/500KV en el nodo B para interconectar dos corredores a diferente nivel de tensión. El tamaño y el costo de los transformadores de la subestación que debe agregarse en el nodo B se determina a través de un subproblema que aplica procedimientos heurísticos y un algoritmo de búsqueda local. De esta forma, para crear subestaciones nuevas, en un nodo particular, se deben cumplir las dos condiciones siguientes: 1) que exista una confluencia de corredores con niveles de tensión diferentes; y 2) que en la red actual no exista una subestación en dicho nodo con los niveles de tensión requeridos. Si los corredores AB y BD aparecen en una propuesta de inversión con el mismo nivel de tensión, no se agrega una subestación nueva en el nodo B y se asume que las cargas y generadores conectados a este nodo se encuentran a la misma tensión de los corredores.
Codificación de las propuestas de líneas considerando el nivel de tensión
En el problema de planeamiento, las variables de inversión nij representan el número de circuitos nuevos que se deben adicionar en el corredor i-j. Sin embargo, el sistema asume una topología diferente al considerar diferentes niveles de tensión para cada corredor nuevo. Esto se puede observar al comparar los sistemas representados en las figuras 1 y 2. En la figura 2, los nodos B' y D' son nodos nuevos que pueden o no aparecer, respecto al sistema que se muestra en la figura 1. Si aumenta el número de nodos del sistema, aumenta también el número de variables de decisión, ya que entonces deben también considerarse las variables asociadas a las subestaciones.
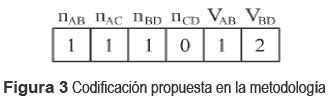
La metodología propuesta divide el análisis en dos fases. En la primera fase, el AGCB propone la adición de circuitos tanto en los corredores nuevos como en los existentes, y en el caso de corredores nuevos, adicionalmente propone un nivel de tensión para su operación. En la segunda fase, crea y determina la capacidad de las subestaciones nuevas que el sistema requiere. De otro lado, para interactuar con el sistema de la figura 1, el AGCB utiliza un vector de variables de decisión como el mostrado en la figura 3. En este vector aparecen las variables de decisión asociadas al número de circuitos candidatos que se adicionan a los corredores: nAB, nAC, nBD y nCD, y las variables de decisión asociadas a los niveles de tensión de los corredores nuevos (VAB y VBD). Obsérvese que no se considera modificar el nivel de tensión en corredores existentes.
La propuesta asociada al vector mostrado en la figura 3 se interpreta de la siguiente forma: Se propone adicionar un circuito en el corredor AB: nAB=1 y operar este corredor a 230kV (VAB=1); también se propone adicionar un circuito en el corredor BD: nBD = 1 y operar este corredor a 500kV (VBD=2), y se propone adicionar un circuito en el corredor existente AC: nAC= 1 (refuerzo), el cual opera al nivel de tensión que posee este circuito en la red actual: 230KV. En el corredor CD no se hace propuesta de adición: nCD=0
Algoritmo Genético de Chu-Beasley
El AGCB ha mostrado un gran potencial en su utilización para encontrar la solución del problema de planeamiento de la expansión de redes de transmisión como se muestra en [2]. El AGCB utilizado en este trabajo fue inicialmente propuesto para resolver el problema de asignación [7]. El AGCB implementado para el problema de planeamiento de la expansión del sistema de transmisión está formado por las siguientes partes. A) Generación de la población inicial: Los algoritmos genéticos presentan una mejor respuesta cuando una parte de la población inicial es generada usando técnicas heurísticas [3]. En este trabajo se utilizan combinaciones de criterios basados en sensibilidad. B) Operador de Selección: En el AGCB se utilizó selección- por torneo. En este, se seleccionan k individuos de la población para realizar dos torneos, y los ganadores de cada torneo se recombinan para generar un descendiente. Estos transmiten parte de sus características al descendiente que es candidato a formar parte de la siguiente generación. C) Operador de Recombinación: En este trabajo se aplica recombinación de un punto. Para esto se selecciona aleatoriamente un número p entre uno y el número de corredores de transmisión menos uno. En el ejemplo de la figura 4, se selecciona un número entre 1 y 3. Para conformar el descendiente, se toman los contenidos de los primeros p corredores del padre 1 y los últimos (n-p) elementos del padre 2. Dado que cada corredor nuevo tiene asociada una tensión, esta acompaña siempre al corredor en el proceso de intercambio.
D) Operador de Mutación: En el AGCB se muta un solo individuo, y se altera 1 o más genes del vector de decisión (descendiente obtenido en el proceso de recombinación) de acuerdo al porcentaje o tasa de mutación (figura 5). En este proceso participan tanto los genes de número de líneas por corredor como los que especifican el nivel de tensión. La modificación en el gen escogido depende de un criterio heurístico. Se define un corte de carga de referencia (maxcor) y si la propuesta presenta un corte de carga mayor a dicho valor, se prioriza la adición sobre la remoción de circuitos y la elevación sobre la reducción o conservación de la tensión, respetando siempre el número máximo de circuitos permitidos por corredor.
E) Mejoría local de un individuo: En el planeamiento de la transmisión, luego de la etapa de mutación, el descendiente puede ser sometido a un análisis especial en el que puede mejorarse la función objetivo y/o disminuir la infactibilidad. El individuo se somete a un análisis basado en sensibilidad, para observar posibles corredores donde se hace necesario el uso de adiciones, disminuyendo la infactibilidad. Esto se logra usando un algoritmo heurístico constructivo basado en la propuesta de Villasana-GarverSalon [8]. Posteriormente, para mejorar aún más la solución parcial, se aplica un procedimiento que identifica elementos redundantes en el sistema, es decir, circuitos que al ser removidos no causan ningún efecto adverso en la calidad de la solución. Para lograr este propósito, se resuelve la red sucesivamente, retirando cada vez una de las líneas adicionadas en la propuesta, y se verifica la importancia de cada adición por separado. El proceso de eliminación de líneas de transmisión se realiza en orden decreciente de costo. F) Alteración de la población: En la etapa final, un descendiente que cumple diversidad (descendiente difiere de todos los individuos de la población) puede reemplazar un individuo de la población actual en los siguientes casos. 1) El descendiente es infactible y en la población existen individuos infactibles con mayor infactibilidad, 2) El descendiente es factible y en la población existen individuos infactibles. En los anteriores casos se reemplaza al individuo más infactible de la población, y 3) El descendiente es factible y en la población solo existen individuos factibles, algunos de peor calidad que el descendiente. En este caso el descendiente reemplaza al individuo con peor función objetivo. Si el descendiente es mejor que la mejor solución encontrada en todo el proceso de optimización (incumbente) y no cumple diversidad, se elimina temporalmente la condición de diversidad y se reemplaza por el peor individuo de la población. Los individuos que no cumplen diversidad con él, se eliminan de la población. Este mecanismo se denomina criterio de aspiración. El proceso se detiene si la mejor solución (incumbente) no mejora luego de un número especificado de iteraciones.
Alternativas usadas para mejorar el desempeño del AGCB
Con el propósito de mejorar el desempeño del AGCB, se implementaron las dos alternativas siguientes:
Alternativa 1: Uso de variables duales de las restricciones de flujo de potencia en conjunto con una técnica de búsqueda local.
En esta alternativa, las reactancias y las capacidades de las subestaciones se calculan usando una técnica heurística aplicada en cuatro pasos: en el primer paso se colocan temporalmente todas las reactancias de los transformadores en cero y se dejan los valores de sus capacidades de potencia ilimitados. En un segundo paso se aplica un flujo de carga DC al sistema resultante y se calculan los flujos de potencia que circulan entre los nodos donde existan subestaciones o donde estas se requieran. La cantidad de transformadores requeridos en cada subestación se calcula de forma aproximada a través del siguiente índice de sensibilidad:

Donde fij es el flujo que circula entre los nodos donde existe o se requiere un transformador y  . es su capacidad máxima. Luego, se puede establecer el número de transformadores que posiblemente sean necesarios aproximando el resultado de (2) al entero inferior más cercano. En el tercer paso, el modelo DC es aumentado en las siguientes restricciones:
. es su capacidad máxima. Luego, se puede establecer el número de transformadores que posiblemente sean necesarios aproximando el resultado de (2) al entero inferior más cercano. En el tercer paso, el modelo DC es aumentado en las siguientes restricciones:

Donde los nij son los valores de circuitos adicionados por la heurística y los n0ij son los circuitos existentes en el corredor en la red inicial. Si la cantidad de transformadores adicionados por la heurística más la cantidad existente en la red base es insuficiente, las variables duales de las restricciones del tipo 3, se hacen diferentes de cero, indicando que se requieren más adiciones. De esta forma se puede guiar el proceso de una forma más adecuada, identificando los transformadores que están al límite de su capacidad de potencia activa. Finalmente, en el cuarto paso, se utiliza un procedimiento de búsqueda local, basado en un microgenético, que considera como variables únicamente a las subestaciones que se encuentran en su límite de capacidad. De esta forma se realiza una búsqueda en la vecindad de la configuración inicial para identificar combinaciones que mejoren el funcionamiento global de la red. El algoritmo microgenético tiene un diseño que requiere de poco esfuerzo computacional, y está basado en el algoritmo genético simple de la siguiente forma: 1) población inicial: creada de forma aleatoria, 2) Los elementos de la población deben discrepar en al menos un transformador de transmisión, 3) Al ser una técnica de búsqueda local exclusiva para transformadores, se limita la adición de recursos a pocos elementos, 4) Selección: se seleccionan aleatoriamente dos individuos. No existe torneo, 5) Recombinación: se recombinan los individuos seleccionados usando intercambio de información entre los cromosomas, de un único punto, 6) La tasa de mutación debe ser alta, 7) Reemplazo: sigue las mismas características del AGCB propuesto, sin embargo no contiene la etapa de aspiración, 8) Penaliza la demanda no atendida y 10) Número generaciones debe ser bastante bajo.
Alternativa 2: Un procedimiento heurístico combinado con una búsqueda local.
Esta alternativa es similar a la anterior, con la diferencia que no usa las variables duales y, por lo tanto, considera en las variables del microgenético todas las subestaciones presentes en la propuesta de inversión.
Resultados
A continuación se muestran los resultados obtenidos con la codificación propuesta y cada una de las alternativas de cálculo de la capacidad de las subestaciones. Se usó como sistema de prueba el sistema sur brasilero de 46 barras y 79 corredores de la literatura especializada [9], que se denominará en adelante sistema sur46A. A partir de este sistema se crean dos sistemas nuevos: el sistema sur brasilero de 46 nodos con demanda aumentada, respecto al sistema original, y que conserva los niveles de tensión del sistema inicial, que se denominará sistema sur46B; y el sistema sur46C que tiene la demanda modificada del sistema sur46B pero que permite que los corredores nuevos puedan operar a 230KV o a 500KV. Los datos de los sistemas sur46B y sur 46C pueden ser consultados con los autores. El problema de planeamiento del sistema de transmisión se resuelve implementando los procedimientos heurísticos descritos anteriormente, el AGCB y el flujo de carga DC, en un programa de computador escrito en FORTRAN. Para comparar los resultados obtenidos también se resuelve el problema usando el solver GLPK [10] el cual utiliza en su interior una técnica exacta. A continuación se presentan los resultados obtenidos.
Alternativa 1: Se prueba sobre el sistema sur46C encontrando una solución de 167'130.000 US$ y requiriendo un tiempo de cómputo de 222,16 segundos. La configuración encontrada es:

En la representación anterior, Tij es el número de transformadores adicionados en las subestaciones existentes ó propuestas, en el caso base (sur46A). Ti es el número de transformadores adicionados en una subestación nueva que no aparece en el caso base y que se adiciona en el nodo i. De otro lado, nij/kV indica que allí se presentan diferentes alternativas en niveles de tensión, donde i-j/kV indica el corredor y el nivel que se utilizó. Si solo se indica nij quiere decir que ese corredor existe en el caso base. Se aclara que si existe una propuesta de adición de una línea de transmisión entre dos subestaciones, este se conecta a los nodos correspondientes a su tensión.
Alternativa 2: Se prueba sobre el sistema sur46C encontrando una solución de 165'701.000 US$ y requiriendo un tiempo de cómputo de 452,37 segundos. La configuración encontrada es:

Al utilizar el sistema de prueba sur46B, es decir, al eliminar la posibilidad de seleccionar el nivel de tensión de los corredores nuevos, se encuentra una solución v= 177'383.000 US$, con la siguiente configuración:
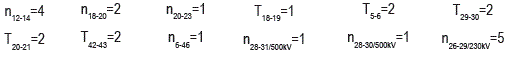
Al comparar los resultados de los sistemas sur46B y sur46C se observa que la solución de 177'383.000 US$ se reduce a la solución de 165'701.000 US$. Esto quiere decir que al considerar el nivel de tensión como variable en los corredores nuevos, se puede obtener una solución con menor costo de inversión, justificando la inclusión de estás variables en el problema de planeamiento. Puede observarse que la solución de 165'701.000 US$ agrega una subestación nueva respecto a la solución de 177'383.000 US$. Esta subestación: T26=2 es una subestación de 230KV/500KV. También se modifica el nivel de tensión del corredor 26-29 de 230KV, del caso base, a 500KV, usando la nueva propuesta. Finalmente se utilizó un solver disponible de uso público, denominado GLPK [10], para resolver el sistema sur46C, usando el modelo lineal disyuntivo para representar la red de transmisión [6], el cual permite convertir el problema de programación no lineal entero- mixto PNL-EM en un problema de programación lineal entero-mixto PL-EM, que el GLPK logra resolver con éxito. El GLPK encuentra la misma solución hallada con la alternativa 2 (de 165'701.000 US$) en un tiempo de 10,41 horas. Esta prueba muestra la importancia de resolver los problemas de planeamiento usando metodologías híbridas: procedimientos heurísticos más técnicas metaheurísticas y procedimientos de búsqueda local. En este caso la calidad de la solución encontrada por la alternativa 2 y por el solver GLPK es la misma pero el tiempo de cálculo se reduce de 10,41 horas a 7.54 minutos.
Conclusiones
Al considerar la posibilidad de seleccionar el nivel de tensión en los corredores nuevos, en el problema de planeamiento de la expansión de la red de transmisión, se aumenta considerablemente el tamaño del espacio solución que las técnicas de optimización deben explorar, haciendo el problema más difícil de resolver. El aumento de la complejidad del problema, sin embargo, es justificable como se mostró en las pruebas con el sistema sur brasilero de 46 nodos, ya que la solución obtenida es mejor que la que resulta sin considerar la tensión como otra variable del problema.
En la medida que se agreguen más variables al problema de planeamiento, y aumente su complejidad, se hace necesario desarrollar nuevas alternativas de solución que permitan reducir el espacio de soluciones. En este trabajo se muestra una opción que permite eliminar y luego reintroducir las subestaciones del sistema eléctrico, con el objetivo de reducir el tamaño del vector de variables de decisión. Con las propuestas presentadas se logra disminuir en alto grado la ubicación estocástica de transformadores haciéndola más determinística al utilizar una heurística basada en sensibilidad combinada con una búsqueda local.
La metodología empleada encuentra la solución óptima del sistema sur46C usando la alternativa 2, ya que esta permite una mayor exploración en la vecindad en el cálculo de la capacidad de las subestaciones. La alternativa 1, a pesar de no encontrar la solución óptima, se comporta con gran robustez, y encuentra soluciones de buena calidad.
Se observa una gran distancia, en tiempo de cómputo, entre las denominadas técnicas exactas y las técnicas híbridas basadas en metaheurísticas. Esto se hace más evidente en la medida en que el tamaño del sistema aumenta.
Agradecimientos
Los autores desean agradecer al programa Jóvenes Investigadores de Colciencias y al grupo de planeamiento de la Universidad Tecnológica de Pereira por el soporte y apoyo suministrado para la realización del presente proyecto.
References
1. G. Latorre, R. Cruz, J. Areiza. ''Classification of publications and models on transmission expansion planning''. IEEE Transactions on Power Systems. Vol. 18. 2003. pp. 938-946. [ Links ]
2. A. Escobar, R. Romero, R. Gallego. Transmission Network Expansion Planning Considering Multiple Generation Scenarios. IEEE/PES, Transmission and Distribution Conference and Exposition in Latin America. 2008. pp. 1-6. [ Links ]
3. A. Escobar, R. Gallego, R. Romero. ''Using traditional heuristic algorithms on an initial genetic algorithm population applied to the transmission expansion planning problem''. Revista Ingeniería e Investigación Universidad Nacional de Colombia. Vol. 31. 2011. pp. 127-143. [ Links ]
4. S. Jalilzadeh, H. Shayeghi, M. Mahdavi, H. Hadadian. ''A GA Based Transmission Network Expansion Planning Considering Voltage Level, Network Losses and Number of Bundle Lines''. American Journal of Applied Sciences. Vol. 6(5). 2009. pp. 970-977. [ Links ]
5. A. Domínguez, A. Escobar, R. Gallego. ''Propuesta de reduccion de modelo para el problema de planeamiento de la expansion de la transmission''. Revista Scientia et Technica, Universidad Tecnologica de Pereira. N°. 49. 2011. pp. 7-13 [ Links ]
6. A. Escobar, R. Romero, R. Gallego. Modelos usados en el planeamiento de la expansión a largo plazo de sistemas de transmisión de energía eléctrica. Ed. Taller de publicaciones Universidad Tecnológica de Pereira. Pereira (Colombia). 2010. pp. 22-72. [ Links ]
7. P. Chu, J. Beasley. ''A genetic algorithm for the generalized assignment problem''. Computers Operations Research. Vol. 24. 1997. pp 17-23. [ Links ]
8. R. Villasana, L. Garver, S. Salon. ''Transmission network planning using linear programming''. IEEE Transactions on Power Apparatus and Systems. N°. 2. 1985. pp. 104. [ Links ]
9. A. Escobar. Planeamiento dinámico de la expansión de sistemas de transmisión usando algoritmos combinatoriales. Tesis de Maestría. Programa de ingeniería Eléctrica. Universidad Tecnológica de Pereira. Pereira, Colombia. 2002. pp. 120-125. Disponible en: http://www.utp.edu.co/~aescobar/PlaneamientoDinamico.pdf. [ Links ]
10. A. Makhorin. GNU Linear Programming Kit (GLPK). Disponible en: http://www.gnu.org/software/glpk/. Consultada enero 24 de 2012. [ Links ]