ARTÍCULO ORIGINAL

Library for model-based design of image processing algorithms on FPGAs

Biblioteca para diseño basado en modelos de algoritmos de procesado de imágenes en FPGA

Luis Manuel Garcés-Socarrás¹, Santiago Sánchez-Solano², Piedad Brox Jiménez², Alejandro José Cabrera Sarmiento¹

¹Grupo de investigación de Sistemas Digitales Empotrados, Departamento de Automática, Instituto Superior Politécnico José Antonio Echeverría (CUJAE). CP: 19390. La Habana, Cuba .

²Grupo de Investigación TIC 180, Instituto de Microelectrónica de Sevilla (IMSE-CNM), CSIC-Universidad de Sevilla. CP. 41092, Sevilla, España.

^*Autor de correspondencia: teléfono: + 5 + 37 + 266 33 29, correo electrónico: lmgarcess@electrica.cujae.edu.cu (L. Garcés)

(Recibido el 23 de abril de 2012. Aceptado el 5 de agosto de 2013)

Abstract

This paper describes a library (XSGImgLib) that includes parameterizable blocks to implement low-level image processing tasks on FPGAs. A model­based design technique provided by Xilinx System Generator (XSG) has been used to design the blocks, which implement point operation (binarization) and neighborhood operations (linear and non-linear filtering) in grayscale images. The blocks are parameterizable for input/output data precision, window size, normalization strategy, and implementation options (area versus speed optimization). The paper includes the implementation results obtained after fixing these options and exemplifies the combination of several blocks of the library to build a complete design for image segmentation purposes.

Keywords: Digital image processing, fpga, xilinx system generator, MATLAB/Simulink

Resumen

Este artículo describe una biblioteca de bloques parametrizables (XSGImgLib) para la implementación de tareas de procesado de imágenes en FPGA. Se ha utilizado la técnica de diseño basado en modelos proporcionada por Xilinx System Generator (XSG) para diseñar diferentes bloques de procesado que implementan operaciones puntuales (binarización) y basadas en vecindad (filtros lineales y no-lineales) para imágenes en escala de grises. La parametrización de los bloques permite configurar la precisión de los datos de entrada/salida, el tamaño de la ventana, la estrategia de normalización y distintas opciones de implementación (optimización en área o velocidad). El artículo muestra los resultados de implementación para las diferentes opciones de configuración y ejemplifica la combinación de los bloques de procesado en el desarrollo de un sistema para segmentado de imágenes.

Palabras clave: Procesado digital de imágenes, FPGA, xilinx system generator, MATLAB/Simulink

Introduction

Computer vision systems include techniques for acquiring, processing, analyzing, and interpreting images. Many of the algorithms used for low-level image processing tasks are common, independently of the application field. These low-level image processing operations are computationally costly and they consume large amount of processing time on a CPU, which imposes serious restrictions to achieve real-time requirements. One solution to cope with this handicap is to accelerate these tasks by means of architectures suitable for hardware implementation on reconfigurable devices such as Field Programmable Gate Arrays (FPGAs) [1­2].

Common low-level image processing tasks can be roughly classified, in terms of the locality of their data access requirements, into two categories: point operations and neighborhood operations. A fundamental operation for neighborhood tasks is convolution. Several architectures have been proposed in the literature for linear image filtering based on convolution techniques. These approaches employ multipliers and adders or MAC (Multiply and Accumulate) blocks. Both techniques are used in the two architectures presented in [3], which are parallel, programmable, scalable, and can be implemented on FPGAs or Digital Signal Processors (DSPs). Another example of a MAC-based architecture for VLSI integration to perform convolution is used in the Integrated Circuit IMSA110 [4]. A bi-dimensional convolution core for video applications suitable for low-cost FPGA implementation (Spartan XL family) and being capable of processing real-time PAL video is proposed in [5]. The work described in [6] presents a framework for developing efficient hardware solutions for image processing applications based on hardware skeletons. A hardware skeleton is a parameterized high-level description of a task-specific architecture.

Among neighborhood operations, non-linear image filtering is crucial to perform certain tasks such as noise removal. In median filters, the pixel under study is replaced by the median of the pixels in the processing window. Rank order filters are generalized forms of median filters where the output is the element with rank R, that is, the R^th smallest element. Thus, a median filter with window size 2N + 1 is a rank order filter with rank R = N + 1. In [7], pipeline architectures for computing non-recursive and recursive median filters are described. One of these architectures is used in [8] to develop an Intellectual Property (IP) block that implements a two-dimensional rank order filter for Xilinx FPGAs. This IP core is parameterizable for input/output data precision, color standard, window size, and maximum horizontal resolution. The user can also configure some implementation options. A particular architecture for median filters with a window size equal to 3x3 is described in [3].

The development of Electronic Design Automation (EDA) tools and its integration with MATLAB/Simulink facilitate the design of DSP systems in FPGAs. Furthermore, these tools support the use of model-based techniques that speed up the description and verification stages in comparison with traditional designs that are described with Hardware Description Languages (HDL). XSG is one of these tools, which incorporates a wide variety of building blocks that are grouped into libraries according to their function. In the DSP library, a 5 × 5 filter block that performs linear filtering in grayscale images is provided [9]. Up to nine different filters can be selected by changing the mask parameters on the block. The architecture is completely programmable since the user can rewrite the memory with new coefficients. In [10], a design flow based on XSG is used to implement a color space transform from RGB to YCbCr in video systems. An architecture for linear image filtering using XSG is presented in [11].

This paper describes the use of the model-based design technique provided by XSG to develop a cell library that includes parameterizable blocks for image processing tasks. First, its provides some fundamental concepts of digital image processing and introduces the model-based design technique provided by XSG. Also, its describes the image processing library, called XSGImgLib, as well as the main features of the architectures that implement the blocks. Finally, its exposes the implementation results of the library blocks, comparing them with other available similar blocks, and includes an example system design using XSGImgLib and some concluding remarks of this work .

Fundamentals of digital image processing

A digital image is defined as a bi-dimensional function, A(x, y), with finite amplitude values, where x and y are spatial coordinates. The function A can be represented as a m × n dot matrix (1) [12].

Image processing methods perform different tasks, such as restoration and improvement of pictorial information, to facilitate image interpretation by humans or autonomous sensing systems [12]. These methods are based on the mathematical transformation of the image dots (pixels) depending on the processing window size with the usual values of p and q being 0, 2, 4, 6, etc.

Image processing techniques are usually classified by several aspects: operation complexity, window size, and linearity. The operation complexity includes low- (image acquisition and pre-processing), middle- (segmentation and characteristics extraction) and high-level processing (data recognition, classification and interpretation). The window size (p + 1 × q + 1) involve point (p = q = 0) and neighborhood operations [2]. Operation linearity depends on the image transformation and is classified into linear (convolution and correlation) and non-linear (ranking, threshold and morphological operations).

Linear image processing includes two well-known operations: convolution (2) and correlation (3). Mathematically convolution (*) and correlation (°) are operations on two functions A(x, y) and C(x, y) described as follows:

where C(i, j) is the kernel filter (4), characterized by the coefficients C_ij:

A correlation kernel is a convolution kernel that has been rotated 180 degrees. The selection of the convolution kernel defines the image transformation, which is used for different purposes.

Non-linear image processing replaces the current pixel by a non-linear operation result. Sorting is the main operation of these algorithms [7], [8]. Spatial sorting processing sorts the pixel values in the neighborhood. Depending on the desired position, the current pixel is replaced by the order th element in the sorted set of neighbors [7]. Median filter is a specific case of rank order algorithms where the output is the middle position.

Threshold is a non-linear point operation. It compares the value of the pixel (in a greyscale image) with a pre-defined value (Thr) and adjusts the output pixel to binary values (5).

Mathematical morphology (MM) is the science that studies the spatial structures. MM is commonly used for image processing tasks like edge detection, restoration and texture analysis [1], [12-14]. A morphological operator uses a Structural Element (SE) to perform its operation. One simple change in the SE provides different results using the same operation.

The basic morphological operators are erosion and dilation. Erosion (6) is based on vector subtraction while dilatation (7) uses vector sum, described as follows:

Morphological operations can change the result applying erode and dilate operators in different order. The opening (λ) is the erosion of an object followed by a dilation and the closing is the opposite operation, recovering the original image after applying dilation [13].

Model-based design

Model-based design provides a useful strategy for development of embedded systems. It is based on the use of graphical programming environments (such as MATLAB/Simulink) and EDA tools, which allows considering the whole operational conditions of the system under development. This strategy facilitates the reusability of previous designs and eases the different synthesis and verification stages, thus accelerating the development of new microelectronic products.

XSG model-based design flow provides the interface between Simulink models and Xilinx tools for reconfigurable devices. Figure 1 shows the steps of the XSG design flow. The Simulink model (.mdl) describing the system is compiled by XSG for simulation (using Simulink internal or external simulators) or synthesis (by means of Xilinx's XST synthesis tool). ISE implementation tools obtain the configuration (.bit) file to program the FPGA.

XSG offers three ways for the verification of the design: functional simulation with Simulink, functional and temporal HDL simulations using ISIM or ModelSIM simulators, and HW co-simulation, where the HW part of the design is implemented on a FPGA development board and interacts with the rest of the Simulink model. This option creates a configuration file for the target device and associates it to a new Simulink block. The process allows checking the algorithm functionality using HW in the loop.

XSGImgLib

XSGImgLib is a library for XSG to facilitate the model-based design of image processing systems. As shown in table 1, it includes different blocks for linear processing, non-linear processing and morphological operators. They are grouped according to the window size and the block type (generic or specific). Generic blocks perform more than one operation, while specific blocks are only used for a single optimized operation, increasing the execution speed and reducing the resource utilization.

Linear image processing

Blocks that perform linear filtering are based on the 2D convolution operation. Some square kernels have the property to be symmetric to the principal diagonal (c_ij= c_ij, i ≠ j, and p = q). This property is used to reduce dedicated multipliers and the occupied slices in the programmable device [16]. Figure 2 shows the difference between the convolution architectures. The symmetric architecture replaces multipliers by the same number of adders, reducing the use of specific resources of the FPGA.

Hardware implementations of mathematical operations present an internal delay to obtain a result. When several blocks with different internal delays are combined in a design, the clock period of the system is determined by the slowest block. In order to increase the processing speed, XSG blocks can add pipeline stages that allow reducing the clock period of the design at expense of consuming more logic resources. Selecting the adequate number of pipeline stages, the processing block can be configured to optimize device occupation or system speed.

Some specific convolution kernels are commonly used for certain image processing tasks. This fact allows the creation of processing blocks with specific architectures optimized in area and execution speed [5]. Figure 3 shows the architecture of a specific filter for edge detection. Shift and adders are used in this design since they are faster and less expensive than multipliers.

The result of the convolution must be usually normalized to maintain the intensity levels of the output image in the same range than the original image. This process is carried out by dividing the coefficients of the kernel by the sum of its elements or by the maximum value between the sum of all the positive elements and the sum of all the negative values of the kernel (this second option is employed when the sum of the kernel values is zero).

All the blocks included in XSGImgLib use fixed-point operations. XSG allows the configuration of the number of bits used for the integer and decimal part in each one ofthe blocks. This makes possible the parameterization of the fixed-point data representation in each block of the processing algorithm, reducing the area used in the device at expense of an acceptably minor error. This error is calculated by performing the normalized mean square error (MSE) of the difference between the resultant image and the image obtained in MATLAB with double precision.

Non-linear image processing

XSGImgLib includes a generic sorting block based on the Chakrabarti's architecture for a generic 2D ranking algorithm shown in figure 4 [7]. It is composed of an initial comparator, two kinds of processors, and a rank detector. The initial comparator receives the k new samples in each clock cycle returning the comparison result for the new values. Processors 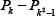receive the k samples, which are compared with the older values in the windows, and update their position. Processors P₀ - P_k-1 calculate the position of the new elements and update the comparison with the other samples keeping a record of the comparison results. This strategy avoids re-comparing all the values to update the position of the elements. Finally, all the sorted values are addressed to the rank detector block which returns the value in the desired position [7].

An optimized element for a 3 × 3 median filter is performed using a three-input comparison block, which returns the values in the sorted order, as shown in figure 5 [3]. The three new values received from the line buffers (L₁ - L₃) in each clock cycle are sorted by the first block. The results are input to new comparison blocks, which reject the values farthest from the middle position in each operation stage.

Morphological operators

Morphological operators are realized using the same architectures employed for sorting blocks but selecting the minimum or maximum values in the processing window. Erosion is implemented by detecting the minimum value of the pixels in the processing window. The architecture in figure 6a stores the pixels in the processing window and every column is addressed to p + 1 minimum value detector blocks where the inputs are fixed by the respective column of the SE. Then, the minimum values of each column in the processing window are obtained and addressed to a minimum value detector block that obtains the final result of the operation.

Dilation is developed in a similar form detecting the maximum value of the pixels in the processing window (figure 6b). Finally, opening and closing operators are implemented combining erosion and dilation blocks and including a parallelization unit (Line Buffer) between the two operations.

Implementation results

The results presented in this section correspond to post-implementation reports of single processing blocks included in XSGImgLib over a Spartan-3A DSP 1800 development board. They depend on the size of the processing image, but allow illustrating some of the configuration options for the generic blocks and optimized specific architectures available in the library.

Non-symmetric vs. symmetric kernels

Symmetric kernels reduce the use of specific multiplier blocks, allowing the implementation of systems with larger window size on small- and medium-size FPGA. The consumption of logic cells (Slices) decreases by between 18% and 22% for blocks with speed optimization, and by 11% for blocks with area optimization. The use of this architecture reduces the number of multiplier from 9 to 6 for a 3 × 3 kernel and from 25 to 15 for a 5 × 5 kernel. On a 3 × 3 convolution block this value represents a 33.33% of specific resource savings (table 2).

Area vs. speed optimization

The configuration of the latency parameter in each calculation block allows selecting the area vs. speed optimization. The multipliers calculate the optimal latency value for a proper design. On a generic convolution filter the optimal latency for a maximum execution speed requires 4 clock cycles to perform an optimized multiplication operation. Using this value as reference, the latency value for area optimization is obtained experimentally. These values are used in the area/ speed optimization adding certain delay cycles to synchronize each mathematical operation.

This optimization criterion reduces by a factor between 29% and 60% the number of used logic cells or increases the execution speed by a factor between 9% and 65%, depending on the processing window size, the kernel type, and the precision of the calculation blocks. Table 3 shows the resource consumption and execution speed for both optimization criteria in a 3 × 3 non- symmetric convolution kernel. Area optimization reduces by 34.42% the number of slices, while the execution frequency increases by 33.93% for speed optimization.

Normalized kernel

The selection of precision parameters in the processing blocks can reduce the resources required by a particular design. Table 4 shows the resource consumption for full precision and normalized convolution blocks. The error introduced by the limitation in the number of bits for fixed-point representation depends on the operation. The block configuration options can be used to obtain an adequate trade-off between resource consumption and MSE.

Generic vs. specific convolution filters

The development of specific filters optimized for a fixed operation considerably reduces the design resources and increases its execution speed. As shown in table 5, the use of these blocks decreases the resource consumption by a factor between 17% and 60%, eliminates the need for specific DSP48A blocks, and increases the frequency form 1.33 up to 3.20 times, depending on the filter.

Generic ranking and specific median filters

As mentioned previously, Chakrabarti's architecture [7] is used to implement the generic sorting filters included in XSGImgLib, while Golston's algorithm [3] supports the specific median filter. The resource consumption for specific and generic blocks (using different window sizes) is shown in table 6. The 5 × 5 filter uses more than 5 times the resources of the 3 x 3 filter. The specific median filters reduces 35% of the logic cells and increases more than 4 times the execution speed compared to the generic 3 × 3 rank filter.

Morphological operators

Table 7 shows the resources consumption for erosion and dilation operators (the values are similar for both blocks). An increase of the size in processing window requires three more times resources and decreases the speed by 28%. The use of logic cells for the opening and closing operators also depends on the image size. The line buffer block adds several slices related to the size of the image. Table 8 shows the results for an image with 64 columns.

Image segmentation using XSGImgLib

Segmentation is a key task in digital image processing that can be easy implemented using the model-based design strategy provided by XSGImgLib (figure 7). In the first stage of the segmentation system the original image (figure 8a) is pre-processed using a specific median filter for noise removal (figure 8b). This stage is followed by a Sobel X-Y filter, for edge detection, and a threshold block, to binarize the image (figure 8c). The smoothing stage reduces the isolate dots in the image and the erosion joins the objects separated in previous steps. Finally, the result is processed through a dilation operator to obtain the segmented image (figure 8d).

As shown in table 9, the system uses the 7.21% of the logic cells available in the FPGA and the 17.26% of multipliers (used in the smoothing phase). The execution speed is 33.612 MHz for 512 × 384 image size, processing a pixel in almost 30 ns and a frame in 5.8 ms (171 fps). This design allows processing images up to WVGA resolution (1024 × 600) in real-time.

Conclusions

XSGImgLib includes blocks that perform point and neighborhood operations to implement low-level image processing algorithms on FPGAs. Blocks for linear image filtering are parametrizable for input/output data precision, window size, normalization strategy, and implementation options. The implementation results on a Xilinx Spartan 3A-DSP shows that a filter with a specific kernel requires fewer resources than a filter with a generic kernel. A 3 × 3 median filter also requires fewer FPGA slices than a generic sorting filter with the same dimensions. In terms of timing, specific architectures for linear and non-linear blocks offer a higher frequency processing. A model-based design, which combines several blocks from the library, is employed for image segmentation purposes.

Acknowledgments

The authors acknowledge the Spanish Agency for International Development (MAEC-AECID) for partially funding this work in the projects PCI D/024124/09 and PCI D/030769/10 (http://www.imse-cnm.csic.es/fortin). P. Brox is currently hired under the post-doctoral grant ''Juan de la Cierva'' from the Spanish government.

The image used in Fig. 8 has been provided with MATLAB Image Processing Toolbox.

References

1. D. Bailey. Design for Embedded Image Processing on FPGAs. 1^st ed. Ed. John Wiley & Sons (Asia) Pte Ltd. Solaris South Tower, Queenstown, Singapore. 2011. pp. 72-74, 231-261, 264-271.         [ Links ]

2. C. Johnston, D. Bailey, P. Lyons. ''A Visual Environment for Real-Time Image Processing in Hardware.'' EURASIP Journal on Embedded Systems. Vol. 2006. pp. 1-8.         [ Links ]

3. M. Wnuk. ''Remarks on Hardware Implementation of Image Processing Algorithms.'' International Journal of Applied Mathematics and Computer Science. Vol. 18. 2008. pp. 105-110.         [ Links ]

4. Datasheet of IMSA110. Image And Signal Processing Sub-System. SGS-Thomson Microelectronics, pp. 1-27. 1992. [Online] Available: http://www.datasheetcatalog.com. Accessed: Nov 4th, 2010.         [ Links ]

5. K. Benkrid, S. Belkacemi. Design and implementation of a 2D convolution core for video applications on FPGAs. 3^rd International Workshop on Digital and Computational Video, 2002. DCV 2002. Proceedings, Clearwater Beach. Florida, USA. 2002. pp. 85-92.         [ Links ]

6. K. Benkrid, D. Crookes, J. Smith, A. Benkrid. High Level Programming for FPGA Based Image and Video Processing using Hardware Skeletons. 9^th Annual IEEE Symposium on Field-Programmable Custom Computing Machines. Rohnert Park. California, USA. 2001. pp. 1-8.         [ Links ]

7. C. Chakrabarti. ''High sample rate array architectures for median filters.'' IEEE Transactions on Signal Processing. Vol. 42. 1994. pp. 707-712.         [ Links ]

8. G. Szedo. ''Two-dimensional rank-order filter by using max-min sorting network.'' Xilinx Application Notes. Vol. 953. 2006. pp. 1-17.         [ Links ]

9. Documentation of Xilinx, User Guides. Xilinx Sytem Genetaror for DSP Reference Guide. 2010. pp. 44-47, 51-54, 75, 86-88, 116-119, 207-210, 223, 22. [Online] Available: http://www.xilinx.com/tools/sysgen.htm Accessed: Nov 21^th. 2011.         [ Links ]

10. T. Saidani, D. Dia, W. Elhamzi, M. Atri, R. Tourki. ''Hardware Co-simulation For Video Processing Using Xilinx System Generator.'' Proceedings of the World Congress on Engineering 2009. Vol. 1. 2009. pp. 3-7.         [ Links ]

11. A. Sánchez, R. Alvarez, S. Sánchez. ''Architecture for filtering images using Xilinx system generator.'' International Journal of Mathematics and Computer in Simulation. Vol. 1. 2007. pp. 101-107.         [ Links ]

12. R. González, R. Woods. Digital image processing. 2^nd ed. Ed. Prentice Hall. Upper Saddle River, NJ, USA. 2002. pp. 66-70, 116-134, 205-208, 283-302, 308-313, 519-560.         [ Links ]

13. P. Soille. Morphological Image Analysis: Principles and Applications. 2^nd ed. Ed. Springer-Verlag. Berlin Heidelberg, Germany. 1999. pp. 1-4, 6-8, 17-26, 63-70, 80, 105-109, 267-268, 319.         [ Links ]

14. A. Nelson. Implementation of image processing algorithms on FPGA hardware. Master Thesis, Vanderbilt University. Tennessee, United States of America . 2000. pp. 11-22, 28-39.         [ Links ]

15. A. Adario, E. Roehe, S. Bampi. Dynamically reconfigurable architecture for image processor applications. Proceedings 1999 Design Automation Conference (Cat. No. 99CH36361). New Orleans, LA, USA. 1999. pp. 623-628.         [ Links ]

16. R. Turney. ''Two-Dimensional Linear Filtering''. Xlinx Application Notes. Vol. 933. 2007. pp. 1-8.         [ Links ]