ARTÍCULO ORIGINAL

Total Lagrangian Finite Element Formulation of the Flory-Rehner Free Energy Function

Formulación de Elemento Finito Total Lagrangiano de la Función de Energía Libre de Flory-Rehner

Mario J. Juha^*

Department of Civil & Environmental Engineering, University of South Florida (USF). CP. 33620. Tampa, USA.

^*Autor de correspondencia: tel: + 1+813 + 9745902 , fax: + 1+813 + 9742957 , correo electrónico: mjuha@mail.usf.edu (M. Juha)

(Recibido el 16 de febrero de 2012. Aceptado el 11 de octubre de 2013)

Abstract

The total Lagrangian finite element implementation of the Flory-Rehner free-energy function in the framework of a hyperelastic material model is addressed. It is explicitly given all the equations required to implement this material model in an implicit nonlinear finite element analysis, particularly, it is shown how to derive the so-called algorithmic or consistent linearized tangent moduli in the Lagrangian description. Some analytical and numerical results for different boundary-value problems are presented to validate the implementation.

Keywords: Deformation gradient, incompressibility, network, solvent, gels

Resumen

Se trata la implemetación total Lagrangiana en elemento finito de la función de energía libre de Flory-Rehner en un marco de un modelo de material hiperelastico. Explícitamente se dan todas las ecuaciones requeridas para implementar este modelo de material en un análisis de elemento finito no lineal, particularmente, se muestra como derivar el llamado modulo tangente consistente o algorítmico en una descripción Lagrangiana. Algunos resultados analíticos y numéricos para diferentes problemas de valor de frontera son presentados para validar la implementación.

Palabras clave: Gradiente de deformación, incompresibilidad, red, solvente, geles

Introduction

Flory-Rehner gels are a kind of soft matter that swell/shrink spontaneously due to a change of the chemical potential in the environment [1]. These gels are composed of a three dimensional polymeric network and small solvent molecules that can migrate in and out of the polymeric chains. The bonds between solvent and polymeric molecules can be thought as physical bonds on the order of Van der Waals forces [2]. Flory- Rehner gels are highly compressible elastic solids with a non-linear material behavior that undergoes large deformations when they are in contact with a solvent at a different chemical potential. Therefore, due to these nonlinearities, it is not an easy task to develop simple theories to analyze them for general cases. Analysis of swelling of inhomogeous gels has been an active topic of study that dates back, at least, since the pioneering work of [3] in the late 70's, when they tried to estimate, analytically, the characteristic time of swelling. Of particular interest is the mathematical work presented in [4, 5]. More recently in [6, 7] is considered a continuum model for chemically induced volume phase transitions in hydrogels that allows for a sharp interface separating swelled and collapsed phases for the underlying polymer network. They used a hybrid eXtended-Finite Element/Level-Set method for obtaining approximate solutions to the governing equations for a two-dimensional model and get an estimate of the response time for swelling. Most notable is the recent work done in [8, 9, 10], they presented a simple theory of coupled molecular migration and large deformation within the framework of non-equilibrium thermodynamics where all the fields are given as a function of the material coordinates. They implemented a hyper-elastic material model using the user supplied routine UHYPER in the commercial package ABAQUS. In [11, 12] the previous theory is reformulated and implemented using the user supplied routine UMAT of ABAQUS to analyze surface instabilities of confined gels layers. The intent of this paper is to address the continuum mechanics theory and finite element implementation of a Flory-Rehner gel in a total Lagrangian framework. Although the theory presented in this paper is not new, still it has not been fully studied and to the knowledge of the author, there is not a reference where explicitly a linearization of the internal nodal forces have been done in a total Lagrangian formulation for a Flory-Rehner gel. However, in [11] a tangent modulus tensor for the same material studied here was explicitly presented for current configuration. Someone could argue that a series of pull-back operation [13] can be applied to the tangent modulus in the deformed representation such that we could transform it into the total Lagrangian formulation. Nevertheless, we have decided to present the entire structure of the total Lagrangian implementation. Following same lines as in [8, 14], we presented a purely mechanical theory of coupled species transport and large elastic deformation in a continuum mechanics approach.

General setupg

Let introduce a fixed right-handed Cartesian coordinate system as presented in figure 1, with orthogonal unit base vectors, E_i, e_i, i = 1,2,3 for the reference and current configuration, respectively. Select Ω₀ as the volume occupy by the body in the reference state and Ω as the volume occupy by the body in the current state. We will assume that there exist a one-to-one and smooth mapping, X=X^-1 (x,t), between the reference and current configuration for all time, t ≥ 0. The tensor field is referred as the deformation gradient and should satisfy the requirement that J = det F > 0 for all t. The latter guarantee that the inverse motion, X = ^-1 (x, t) exist and it is unique. The boundary of the body is divided into three parts as follows: Γ_h ∪ Γ_t ∪ Γ_u=Ø and with the restriction that Γ_h ∪ Γ_t ∪ Γ_u=Ø. In the following subsections we will review the balance principles.

Molecular incompressibility for gels

The gel is a continuum body that could have a dramatic change in volume, therefore it is considered a compressible solid. Independently, the long chain network of the polymer and the solvent molecules that constitute the gel are modelled as incompressible materials. Then, considering the incompressibility of the polymer and solvent molecules, and according to [14], the molecular incompressibility is defined in equation (1).

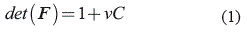
Where, vC is the volume of the small molecules in the gel divided by the volume of the dry network. Figure 2 presents a pictorial definition of the hydrogel. Note that, although, the system is incompressible, the hydrogel is compressible, because the solvent particles could move in and out of the network. The kinetics of the swelling gels is presented in a pictorial form in figure 3. In the theory presented in this section, it is studied the state when the gel is in equilibrium with the solvent. In this steady state, there is no change in volume, unless a perturbation in the system is applied.

Mathematical derivation of the molecular incompressibility

The hypothesis used here is that there is no void space or discontinuities in the gel. Therefore, the differential volume of the gel is given by equation (2).

Equation (3) is obtained expressing the volume of the gel and the network with respect to the reference state (Lagrangian point of view) and noticing that V⁰ refers to the volume at time t=0 and V refers to the volume at time t ≥ 0.

Also, note that dV⁰_network = dV⁰_gel(see, i.e., figure 3) and the incompresibility of the dry network have been used. Dividing equation (3) by dV⁰_(network) and noticing that is the volume of the small molecules (solvent) in the gel divided by the volume of the dry network. We will approximate the latter, using vC. Where v is the volume of the solvent molecules and C is a scalar field that describes the distribution of the solvent molecules in the gel. With these assumptions, it is obtained the molecular incompressibility condition given in equation (1).

Flory-rehner free energy function

For the purpose of this analysis we will work with the Flory-Rehner free energy function [9], defined by equation (4)

Where N is the number of polymeric chains per reference volume, kT is the absolute temperature in units of energy, is a dimensionless measure of the enthalpy of mixing. In equation (4) there are two independent variables, F and C. Therefore, the use of equation (4) in a variational principle would need a two-field variational principle [13]. Alternative, the use of a Lagrange transform and the molecular incompressibility to transform equation (4) into a function of the deformation gradient only can be used. When the gel equilibrates with the solvent and the mechanical load, the chemical potential of the solvent molecules, μ, is homogeneous in the external solvent and inside the gel, as presented in figure 4. In thermodynamics, the chemical potential is defined by equation (5), preserving entropy, volume and number of particles constant.

Using equation (5), the Legendre transform and the molecular incompressibilty, it is obtained equation (6). Later we will replace C using the molecular incompressibility condition.

A combination of equation (4), equation (6) and equation (1) gives the desired free energy function as presented in equation (7).

Where I=F:F is the first invariant of the right Cauchy-Green deformation tensor. Seems like there is an inconsistency in equation (7) when J=1, that is, solvent free, but it is not true because equation (7) is bounded, in other words, lim_F=IŴ (F, μ)=0.

Hyperelastic constitutive equation for gels

We will consider the hydrogel as a hyperelastic material, therefore the constitutive equation is given by equation (8), where is known as the first Piola-Kirchhoff stress tensor [13] or nominal stress.

Next step is to replace equation (7) into equation (8) and take the derivative. Following, it will be used equation (9)

For simplicity, the derivative of the free energy function are divided in three parts, given by equation (10), equation (11) and equation (12).

Part 1

Part 2

Part 3

Replacing part 1, part 2 and part 3 into equation (8), it is obtained the constitutive equation for this particular problem as given in equation (13).

Note that the first Piola-Kirchhoff stress tensor is singular when the network is solvent free. Therefore, equation (13) cannot be used in the reference state dry network. In the following section is proposed the use of a free-swelling as a reference state.

Free swelling as a reference state

To avoid the singularity in the free-energy function, we choose as our reference state the free swelling state [9]. We will need to specify equation (13) in terms of this state. To achieve this, it will be used a multiplicative product of the deformation gradient, as in figure 5.

With reference to figure 5 and with the definition of the deformation gradient it is arrived to equation (14)

Where, in the last step we have replaced dx' by F⁰dX and dx' is a differential vector in the free swelling state, dx is a differential vector in the swelling state and dX is a differential vector in the reference state (dry network). Therefore, the multiplicative product of the deformation gradient is given by equation (15)

The motion between the dry network state and the free swelling state is given by equation (16)

Where λ₀ is the free swelling stretch. Using equation (16) and the definition of deformation gradient, we get the deformation gradient between the free swelling state and the dry network state, equation (17), where I is the identity matrix.

Free swelling stretch

For the evaluation of the free swelling stretch, equation (18), we will use equation (13) and the fact that in the free swelling state P = 0, where 0 is the zero matrix and F=F₀

Therefore using equation (18), the equation (19) is obtained

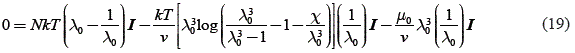
It reduces to one equation with one unknowns as presented in equation (20)

Equation (20) is a nonlinear equation and could be easily solve using a Newton-Rahpson algorithm. Note that we have used the property: log(u/v)=-log(v/u)

Free energy as a function of the free swelling state

It is desired to reformulate equation (7) as a function of the free swelling state, that is, F' and μ. Before proceeds, it is important to clarify that the free energy function is defined per unit reference volume. In the following, U is the strain energy in the swelling state, V₀ is the reference volume (dry network) and V' is the volume in the free swelling state. Then, equation (21) gives the desired equations,

Note that the strain energy should be the same for both cases, the difference in the free energy function is due to the choice of the reference state. Notice that V₀ and V' can be related by mean of the Jacobian. Also, the Jacobian, equation (22), for the free swelling state is constant.

Noticing that J₀=λ₀³, then, it is arrived to equation (23),

Free energy

The free energy as a function of the free swelling state, equation (24), is obtained using equation (7), equation (23) and the expressions obtained in previous sections.

where I' is the first invariant of the tensor gradient in the free swelling state. In the free swelling state, J'=1, but it does not cause problem, unless, λ₀=1, that is, the gel is incompressible, therefore, violating our assumption of compressibility.

Constitutive equation in terms of invariant and elasticity tensor

In this section is introduced the most general form of a stress relation and elasticity tensor in terms of the strain invariant for the Flory-Rehner free energy function as is applied to hyperelastic material models. The most general expression for the evaluation of stresses using equation (24) is given in equation (25)

where S is the second Piola-Kirchhoff stress tensor, C= F^T F is the green deformation tensor tensor, I₁ and I₃ are the invariants of C and I is the identity matrix. For the description of isotropic hyperelastic materials at finite strain considering equation (24) in the coupled form, with invariant, I₁ and I₃, the most general elasticity tensor is given by equation (26) and equation (27)

Where the definitions of the symbols used are given in equation (28) to equation (31)

Notes about derivatives of the Flory-Rehner free energy function respect to invariants of Green deformation tensor.

All the equation on this section assumed that the Flory-Rehner free-energy function is a function of the first and thirds invariants of C. However, equation (24) is expressed as a function of I₁ and J= det F=I₃^(1/2). Therefore, to differentiate W respect to I₃ the chain rule is used and results are presented in equation (32) to equation (35).

Variational form of the equation of motion and finite element equations

The weak form of the boundary-value problem is also known as the principle of virtual work in mechanics of materials. In this method we want to express the boundary-value problem in a variational form (integral form) instead of the original differential form. Therefore, the requirements of the continuity of the trial solution is lower than in the strong form, it suggest the name weak form. For a more detail explanation and a proof that both formulations are equivalent, see [15].

A formal statement of the weak form of the boundary-value goes as follows: Given and , find u V such that for all η W, as shown in equation (36)

where σ is a second order tensor defined in terms of u and V, equation (37), is the space for all the test functions (solution space) and W, equation (38), is the space for all the trial functions (variation), such that the following is true,

Figure 6 is a pictorial representation of the trial function. Note that η is arbitrary and the only condition is that must be zero when evaluated at the boundary where the displacement has been specified. We use η as the virtual displacement field δu, defined on the current configuration. Taking this into account we want to recast equation (36) as a function of the variation of the displacement and the Cauchy stress tensor (σ). Considering the symmetry of the Cauchy stress tensor and equation (39),

Where δe is the variation of the Euler-Almansi strain tensor [13] defined in the current state. Substituting equation (39) into equation (36) it is obtained equation (40),

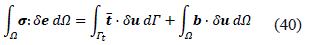
Equation (40) represent the virtual displacement principle's and it clearly state that the internal virtual work should equilibrate the external virtual work. This equation is true for small and large deformation and small or large stress and strain. The use of equation (40) require the specification of a proper material model. The expression of the virtual work in a nonlinear regime has a fundamental difficulty that in most cases does not allow to use it, as is stated in equation (40). This is because, in general, the domain of integration is not known at the current time and the material model used in this paper is nonlinear.

Total Lagrangian formulation

In this paper it is used the Total Lagrangian (TL) formulation to deal with the unknown integration domain. A TL formulation is based on the assumption that there exist an inverse mapping between the current and a reference state which allows us to refer everything to a known reference state at the beginning of the motion. To express the principle of virtual work in the reference state we will use the second Piola-Kirchhoff stress tensor and the Green-Lagrange strain tensor (E). as presented in equation (41).

Equation (41) is the basic expression of the TL formulation used in this paper. Note that the integration is respect to the known reference configuration at time t = 0.

Integration in a finite element solution based on Total Lagrangian approach

Integrals on the reference configuration are related to integrals over the parent element by equation (42)

here the integration is carried out on the parent element domain (ξ) and J_ξ is the Jacobian between the reference configuration and the parent element, as shown in figure 7 for a two dimensional quadrilateral element. Note that, J_ξ does not depend on the current configuration and therefore just need to be evaluated at the beginning of the calculations.

Finite element approximation

To solve approximately the equations shown in previous sections, it will be used an isoparametric finite element discretization. The problem domain is defined by a mesh. Geometry and independent variables are interpolated using compact piecewise linear functions. In general, the geometry and variables will be interpolated using equation (43) for each element in the mesh.

where ξ corresponds to the parent element coordinate, N(ξ) are the standard finite element shape functions [19] and u and û are the vectors of coordinates nodal values and nodal variables, respectively. Then, using the previous interpolations and Voigt notation [16] we can express equation (41) in matrix form and we will call it, the internal nodal force vector and it is presented in equation (44).

where the B_0I express the variation of the Green strain [16, 17] and is given in equation (45) for a three dimensional problem,

and the second Piola-Kirchhoff stress ''vector'' is given by equation (46),

Applying a linearization process to equation (44) and using finite element interpolation, we arrived to equation (47), which corresponds to a system of equations,

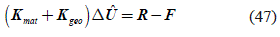
In equation (47) K_mat K_geo and are the well known material and geometric stiffness matrix, respectively and R is the vector of external point forces. These matrices are defined by equation (48) and equation (49),

Where D is the algorithmic tangent modulus ( equation (26) ) in Voigt notation and I is the identity matrix.

Results

Free swelling

Free swelling refers to a gel configuration in which there are no constraints for the motion. To simulate it into a finite element solution we removed the rigid body motion of the body applying proper boundary conditions. Figure 8 shows a comparison between the analytical and finite element results. The gel was simulated using one element as shown in figure 9.

Note also that the displacement field shown in figure 9 was measured respect to the free swelling state because of our implementation of the Flory-Rehner free energy function. According to that, the relation used to calculate the free swelling stretch is given by equation (50)

where λ₀ is the initial free swelling stretch, is the displacement, measure from the initial swelling state, andis the original free swelling cube length.

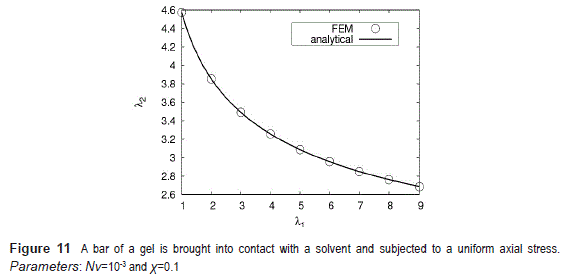
A bar of a gel in contact with a solvent and subjected to a uniform axial stress

In this example a bar of gel is put in contact with a solvent and an axial force was applied to the gel. The longitudinal stretch is given by λ₁ and the traverse stretches are given by λ₂= λ₃. The analytical solution is given in equation (51) and it is used to calculate (using Newton's method) λ₂ for every known value λ₁. The bar was simulated using one finite element as shown in figure 10. The comparison between the analytical and numerical solution is presented in figure 11.

Conclusions

It has been shown some preliminaries results that involves the use of a Flory-Rehner free energy function in a Total Lagrangian framework. The results have shown that the implementation of the material model is working as expected. Further analysis that includes non-homogeneous field should be done. The extremely large deformation in the gel imposes a difficult convergence condition to the finite element solution.

References

1. S. DuPont, R. Cates, P. Stroot, R. Toomey. ''Swelling-induced instabilities in microscale, surface confined poly(n-isopropylacryamide) hydrogels''. Soft Matter. Vol. 6. 2010. pp. 3876-3882.         [ Links ]

2. R. Jones. ''Soft Condensed Matter''. Oxford Master Series in Condensed Matter Physics. 1^st ed. Oxford University Press. Oxford, UK. 2002. pp. 208.         [ Links ]

3. T. Tanaka, D. Fillmore. ''Kinetic of swelling of gels''. J. Chem. Phys. Vol. 70. 1979. pp. 1214-1218.         [ Links ]

4. A. Onuki. ''Theory of pattern formation in gels: Surface folding in highly compressible elastic bodies''. Physical Review A. Vol. 39. 1988. pp. 5932-5948.         [ Links ]

5. A. Onuki. ''Theory of phase transition in polymer gels''. Advances in Polymer Science I. Vol. 109. 1993. pp. 63-121.         [ Links ]

6. J. Dolbow, E. Fried, H. Ji. ''Chemically induced swelling of hydrogels''. Journal of the Mechanics and Physics of Solids. Vol. 52. 2004. pp. 51-84.         [ Links ]

7. J. Dolbow, E. Fried, H. Ji. ''A numerical strategy for investigating the kinematic response of stimulus- responsive hydrogels''. Comput. MethodsAppl. Engrg. Vol. 194. 2005. pp. 4447-4480.         [ Links ]

8. W. Hong, X. Zhao, J. Zhou, Z. Suo. ''A theory of coupled diffusion and large deformation in polymeric gels''. Journal of the Mechanics and Physics of Solids. Vol. 56. 2008. pp. 1779-1793.         [ Links ]

9. W. Hong, Z. Liu, Z. Suo. ''Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load''. Int. J. Solids Struct. Vol. 46. 2009. pp. 3282-3289.         [ Links ]

10. J. Zhang, X. Zhao, Z. Suo, H. Jiang. ''A finite element method for transient analysis of concurrent large deformation and mass transport in gels''. Journal of Applied Physics. Vol. 105. 2009. pp. 093522.         [ Links ]

11. M. Kang, R. Huang. ''Swell induced surface instability of confined hydrogel layers on substrates''. Journal of the Mechanics and Physics of Solids. Vol. 58. 2010. pp. 1582-1598.         [ Links ]

12. M. Kang, R. Huang. ''A variational approach and finite element implementation for swelling of polymeric hydrogels under geometric constraints''. J. Appl. Mech. 2010. pp. 1-12.         [ Links ]

13. G. Holzapfel. ''Nonlinear Solid Mechanics: A continuum approach for engineers''. 1^st ed. Ed. John Wiley & Sons. USA. 2001. pp. 455.         [ Links ]

14. M. Gurtin, E. Fried, L. Anand. The Mechanics and Thermodynamics of Continua. 1^st ed. Ed. Cambridge University Press. USA. 2009. pp. 716.         [ Links ]

15. T. Hughes. The Finite Element Method: Linear Static and Dynamic Finite element Analysis. 1^st ed. Dover, USA. 2000. pp. 672.         [ Links ]

16. T. Belytschko, W. Liu, B. Moran. Nonlinear Finite Elements for Continua and Structures. 1^st ed. Wiley, USA. 2000. pp. 300.         [ Links ]

17. O. Zienkiewicz, R. Taylor. The finite Element Method for Solid and Structural Mechanics. 6^th ed. Ed. Elsevier. 2005. pp. 736.         [ Links ]