Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.73 Medellín Oct./Dec. 2014
ARTÍCULO ORIGINAL
Impacto de la generación eólica en el despacho hidrotérmico de mediano plazo
Impact of wind power in middle-termed hydrothermal dispatch
Sandro Ramos, María Victoria Ramírez-Martínez*, Alejandro-Garcés
Grupo de Investigación en Planeamiento de Sistemas Eléctricos de Potencia, Universidad Tecnológica de Pereira. Carrera 27 Vol. 10-02 Barrio Álamos. AA. 97-C.P. 660003. Pereira, Colombia.
*Autor de correspondencia: María Victoria Ramírez Martínez, correo electrónico: mvictoriaramirez@utp.edu.co
(Recibido el 13 de septiembre de 2013. Aceptado el 18 de octubre de 2014)
Resumen
El presente trabajo describe un modelo de programación lineal y simulación de Monte Carlo para solucionar un problema de despacho hidrotérmico de mediano plazo, a nodo único, con tres distintos escenarios de penetración de generación eólica. Se considera costo del combustible variable en cada período, teniendo en cuenta dos tecnologías: plantas de carbón y de gas con ciclo combinado. Se utiliza un sistema de prueba con dos plantas térmicas, tres hidráulicas y un parque eólico que pueden operar continuamente en el horizonte de planeamiento de 12 meses.
La generación eólica se modela mediante funciones de distribución de probabilidad tipo Weibull, particulares para el sistema colombiano, mientras que la generación hidráulica se modela mediante funciones de probabilidad normal. Los resultados muestran una reducción de los costos de operación de acuerdo a tres escenarios de penetración eólica. El principal aporte de este artículo consiste en introducir simultáneamente el efecto estocástico tanto del viento como de la hidrología en el despacho hidrotérmico.
Palabras Clave: Despacho hidrotérmico, embalse, generación eólica, optimización estocástica, programación lineal, simulación de Monte Carlo
Abstract
This paper describes a linear programming model and Monte Carlo simulation which solve a middle-termed hydrothermal dispatch problem for three different scenarios of wind power penetration. Transmission line effects are neglected. The fuel cost in thermal plants varies in each time period. The test system has two thermal and three hydroelectric plants that can continuously operate during the twelve-months planning term. Wind generation is modeled by using Weibull Distribution Functions particular to the Colombian system, while hydro-generation is modeled by Normal Distribution Functions. Results show costs reduction for the three scenarios of wind power penetration. The main contribution of this paper is to simultaneously introduce the stochastic effect of wind and hydrology in the hydrothermal dispatch.
Keywords: Hydrothermal dispatch, reservoir, wind power generation, stochastic optimization, linear programming, Monte Carlo simulation
Introducción
Un sistema hidrotérmico es aquel en el que la generación hidráulica no es suficiente para satisfacer la demanda y debe apoyarse en la generación térmica para suplir el excedente.
El objetivo del despacho hidrotérmico es determinar un cronograma de operación, es decir, los períodos de tiempo y los niveles de generación de las plantas hidráulicas y térmicas para minimizar el costo de operación del sistema [1]. Este planeamiento puede hacerse, de acuerdo con el horizonte de tiempo, a corto, mediano y largo plazo. Los primeros trabajos sobre despacho hidrotérmico datan de comienzos de la década del 50 [2]. A partir de los 90, se viene introduciendo el efecto de la generación eólica al despacho hidrotérmico [3-5], especialmente en el corto plazo.
En aras de encontrar soluciones al problema del despacho hidrotérmico, en tiempos computacionales razonables, es necesario realizar simplificaciones. En el presente estudio, se adoptan los siguientes supuestos: a) no se tiene en cuenta el efecto de la red de transmisión; b) no se permite racionamiento, c) debe minimizarse el vertimiento, esto es, el agua que pasa a través del canal del embalse y que no se turbina; d) no se opera por encima de los límites de capacidad del sistema; e) tanto al agua como al viento se les asigna costo igual a cero; f) se asumen conocidos: la capacidad máxima de las plantas térmicas e hidráulicas, la demanda futura y el costo del combustible de las térmicas, en cada período de tiempo.
El problema del despacho hidrotérmico, también conocido como coordinación, planeación o asignación hidrotérmica (dispatch, coordination, planning or scheduling) es de tipo estocástico [6], dinámico [7] y acoplado en el tiempo y en el espacio [8]. Cuando se introduce la generación eólica al problema, se adiciona un nuevo efecto estocástico, como resultado de la incertidumbre en la velocidad del viento [9]. El nuevo problema puede adoptar el nombre de despacho eólico hidrotérmico [10]. Las fuentes de energía renovables como la eólica vienen tomando fuerza en el escenario mundial por ser mucho más limpias que las generadas a partir de combustibles fósiles, su tecnología ha venido evolucionando de manera importante por lo que se han hecho más competitivas. [11]. Sin embargo, ese tipo de generación solo representa el 0,33% del total nacional. [12]. Por otro lado, en Colombia ya se han venido adelantado experiencias con generación eólica en la Costa Atlántica (Jepirachi- Alta Guajira) [13] y existe un gran potencial de este recurso en esa zona que se tiene como una alternativa promisoria para la generación de energía que esté comprometida con la conservación del planeta.
A lo largo del tiempo, se han aplicado muy diversas técnicas para resolver el problema de despacho hidrotérmico, tanto exactas como no exactas, entre las que se tienen: los algoritmos de descomposición [14], la programación lineal [15] y no lineal [16], programación dinámica [17], y algoritmos no exactos y técnicas evolutivas o metaheurísticas como búsqueda tabú [18], simulated annealing [19], partículas swarm [20], entre otras [21]. Este explora una solución híbrida basada en la programación lineal, utilizando el lenguaje de programación matemática AMPL (A Mathematic Programming Language) y el subprograma de optimización CPLEX [ILOG, 2001] [22]. El componente estocástico del problema se programa en Matlab, mediante la técnica de Simulación de Montecarlo.
Este artículo presenta un análisis del efecto estocástico de las afluencias y del viento en el costo de operación de un sistema hidrotérmico, en tres escenarios de penetración eólica. Este trabajo está organizado como sigue: En primera instancia se presenta el modelo matemático del despacho hidrotérmico, en segundo lugar el modelamiento estocástico que contiene tres partes: modelamiento del parque eólico, modelamiento de las afluencias, modelamiento de la demanda y modelamiento de los precios del combustible, como cuarto punto los resultados y, finalmente, las conclusiones.
Modelo matemático despacho hidrotérmico
El modelo matemático se basa en la minimización de una función objetivo que contiene el costo de operación de las centrales térmicas y el costo asociado al racionamiento. El problema es restricto y, por lo tanto, deben satisfacerse, en todo momento, las restricciones de balance de energía, de balance hídrico, los límites de generación, los límites de turbinamiento y los de almacenamiento [23]. La restricción de balance de energía contiene implícito el efecto de la generación eólica al restarse de la demanda total, la generación eólica servida, es decir, la generación eólica cuando se produce, se despacha obligatoriamente [24]. No introducir un generador de racionamiento en el modelo, puede conducir a problemas de convergencia, razón por la cual éste se introduce en la ecuación de balance energético. A continuación se presenta el modelo propuesto en este trabajo.
Notación:
t Periodos de tiempo
nct Número de centrales térmicas
nch Número de centrales hidráulicas
costnct,t Costo de operación de la central térmica nct en el periodo t
gnct,t Generación térmica de la central nch en el periodo t
gmaxnct,t Generación máxima térmica de la central nct en el periodo t
ghnch,t Generación hidráulica de la central nch en el periodo tgmaxhnch,t Generación máxima hidráulica de la central nch en el periodo t
crt Costo del racionamiento en el periodo t
grt Generador ficticio o de racionamiento en el periodo t
cvlt Costo del vertimiento en el periodo t
vvnch,t Vertimiento de la central hidráulica nch en el periodo t
dt Demanda promedio en el periodo t
d't Demanda promedio menos generación eólica en el periodo t
Et Generación eólica en el periodo tvnch,t Volumen del embalse de la central hidráulica nch en el periodo t
vmaxnch,t Volumen máximo del embalse de la central hidráulica nch en el periodo t
anch,tAfluencia a la central hidráulica nch en el periodo t
unch,tTurbinamiento de la central hidráulica nchen en el periodo t
umaxnch,t Turbinamiento máximo de la central hidráulica nch en el periodo t
gwi,t Generación del parque eólico i en el periodo t
Función objetivo (1)

Restricciones
1. Balance de energía (2)
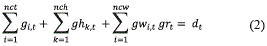
2. Balance hídrico (3)
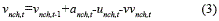
3. Límite de generación térmica (4)

4. Límite de generación hidráulica (5)

5. Generación hidráulica (6)

6. Límite de turbinamiento (7)

7. Límite de almacenamiento (8)

8. Restricción de meta de generación (9)

9. Demanda estocástica (10)

Modelo estocástico
Modelo estocástico del parque eólico
Para la implementación del modelo probabilístico del viento, se consideran los datos medidos en la estación de viento Puerto Bolívar de la península de la Guajira, en Colombia. En este lugar se alcanzan vientos iguales o superiores a 5 m/s durante todo el año y se registra una persistencia en la intensidad de los mismos, lo que hace que sea un lugar adecuado para el aprovechamiento energético del viento [11]. Una de las funciones de distribución de probabilidad más ampliamente usada para modelar el comportamiento estocástico del viento, es la Función de Distribución de Weibull [25]. A partir del valor acumulado de esta función, se obtienen los valores aleatorios del viento que alimentarán la simulación de Monte Carlo. Esta función de distribución acumulada está definida como 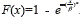 . En la tabla 1 se muestran el factor de escala (β) y el factor de forma (α) para cada función de distribución de Weibull, en cada uno de los 12 mes del año, en Puerto Bolívar, Guajira. En este caso, x es la velocidad del viento.
. En la tabla 1 se muestran el factor de escala (β) y el factor de forma (α) para cada función de distribución de Weibull, en cada uno de los 12 mes del año, en Puerto Bolívar, Guajira. En este caso, x es la velocidad del viento.
La función de distribución acumulada tiene valores entre cero y uno. Se genera un valor aleatorio en este rango, que corresponde a un valor de la función acumulada, denotado como u, y a partir de allí, se obtiene el valor del viento correspondiente, de la ecuación (11), con valores conocidos de α y β para el mes correspondiente.

Con el valor del viento, se calcula la potencia eólica del parque a instalar, a partir de la ecuación (12) [26], donde Cp es el factor que mide la eficiencia del rotor y se calcula de la ecuación (13), la potencia nominal es de 5 MW y la velocidad nominal se asume de 12 m/s. Así las cosas, la eficiencia para el rotor de la turbina propuesta en este trabajo es del 43%.
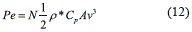

Los parámetros del parque eólico se resumen en la tabla 2.
Modelo estocástico de las afluencias
Para efectos de introducir la incertidumbre de las afluencias, se tiene en cuenta un modelo probabilístico distinto para cada central hidráulica. A continuación se presenta la tabla 3 que contiene los datos de caudal agregado mensual en m³/s [27]. Los caudales de los principales embalses colombianos pueden consultarse en [28]. Los valores son calculados a partir de las afluencias agregadas en cada uno de los embalses, mediante la Función de Distribución Normal (FDN) definida en [29], ecuación (14), donde μ representa la media y σ, la desviación estándar.

La función de transferencia inversa encuentra el valor de la variable aleatoria con una probabilidad dada de ocurrencia en la ecuación 15:

El embalse agregado porcentual, multiplicado por el volumen máximo reportado en cada período se reparte en tres afluentes de las centrales H1, H2 y H3 en cada período, y sus respectivos valores medios y desviaciones estándar se encuentran en la tabla 4.
Simulación de Monte Carlo
Este método consiste en realizar múltiples experimentos con el modelo matemático, es decir, evaluar muchas veces distintos valores de las variables aleatorias del problema para estimar un escenario real [30]. Los pasos del algoritmos son:a) seleccionar las variables aleatorias de entrada (velocidad del viento y afluencias), b) generar un valor xij con probabilidad definida por su función de transferencia inversa, c) evaluar la variable de salida y d) evaluar el criterio de convergencia, que en este caso, será el número máximo de iteraciones (10.000 en total).
Modelamiento de la demanda
La demanda promedio para cada período se muestra en la tabla 5 y en la figura 1 [31] y es la misma para todos los escenarios de penetración eólica.
Modelamiento de los precios del combustible
El costo de las plantas térmicas (de dos combustibles: gas y carbón) se obtuvo tomando como referencia el precio en bolsa de los combustibles en Colombia. El precio del racionamiento se calcula multiplicando el costo de la planta térmica de mayor valor, en cada periodo de análisis, por un factor de 10. La tabla 6 resume los datos.
Resultados
El modelo matemático propuesto se aplica a un sistema de prueba que fue desarrollado por los autores para el presente estudio, con las siguientes características: a) un escenario de generación que considera, para el horizonte de planeación de 12 meses, la operación de dos plantas térmicas: T1 y T2, tres centrales hidráulicas H1, H2 y H3 y una central eólica E1. A las centrales hidráulicas se asocian las afluencias de los ríos RA, RB y RC respectivamente, con una distribución arbitraria porcentual de las afluencias agregadas de los embalses colombianos de 48,32%, 24,16% y 27,52%, respectivamente, pero que son modeladas estocásticamente; la potencia eólica, concentrada en un solo generador equivalente, también se modela estocásticamente; b) un costo, en unidades monetarias UM por megavatio-mes, para las plantas térmicas y para el racionamiento; c) un costo igual a cero, para las plantas hidráulicas y para la planta eólica; d) modelos de probabilidad para cada río; y e) una demanda variable a lo largo del periodo de análisis.
Para todos los periodos se asume el mismo valor de generación máxima. En el caso de las térmicas T1 y T2, los valores son 1000MW y 662,34 MW, respectivamente. Para las hidráulicas, los valores son de 2000MW para H1; 1000MW, para H2; y 1139,47MW, para H3, para una capacidad instalada total hidrotérmica de 5801,87 MW. Dado que se analizan tres escenarios de penetración de generación eólica de 100MW, 200MW y 1000MW, la capacidad total instalada, incluyendo la planta eólica en cada escenario, es de 5901,87MW, 6001,87MW y 6801,87MW, respectivamente. Para cada uno de los embalses se tienen disponibles los volúmenes iniciales, volúmenes finales y máximos, como se muestra en la tabla 7. El modelo bajo análisis permite el uso de los embalses y fija una meta de generación para el último período. Este modelo obliga a los embalses a dejar un volumen predeterminado de agua en el mes 12. Esto se considera una reserva para los años siguientes.
Los datos de turbinamiento máximo se muestran en la tabla 8, al igual que los datos de factor de turbinamiento y potencia máxima en MW.
Las velocidades aleatorias del viento mínimas y máximas en cada una de los escenarios, en la simulación de Monte Carlo se resumen en la tabla 9:
Los resultados experimentales obtenidos para la variable de salida costo en los tres escenarios se muestran en los histogramas que se presentan a continuación, en figuras 2, 3 y 4 para los escenarios 1, 2 y 3 respectivamente.
De los histogramas puede leerse que para el escenario 1, la mayor frecuencia (2.820) correspondió al costo de 1.220.000 UM, para el escenario 2, la frecuencia se situó en el valor 3.030 y el costo correspondiente fue 1.180.000 UM, mientras que en el escenario 3, la frecuencia fue de 2.890 para el costo de 935.000 UM.
La reducción en el costo de la energía, tomando como valor de referencia el escenario determinístico fue de 31,73%, 33,97% y de 47,68% en los valores de mayor probabilidad de ocurrencia. Tanto a la izquierda como a la derecha de esos valores en la distribución de probabilidades, no se encuentran valores de costo superiores al de referencia, para ninguno de los tres escenarios como se observa en la tabla 10.
El modelo estocástico del viento produjo los valores de potencia servida a lo largo de los doce periodos y para cada iteración. Sin embargo, no se presentan histogramas para cada uno de los 12 periodos sino que se agrupan los datos como sigue. Se totaliza la potencia eólica servida a lo largo del año, es decir, se suman las potencias eólicas despachadas de los doce periodos de tiempo en cada iteración.
Se tiene entonces que la potencia eólica despachada en un año, en el primer escenario es de 256 MW, en la mayor frecuencia (2.970), por su parte el segundo escenario el nivel de mayor potencia eólica despachada fue de 543 MW, con una frecuencia de (2.810), mientras que los valores para el tercer escenario fueron de 2.960 MW, en la frecuencia 2.760.
Los niveles máximo, mínimo y de mayor frecuencia de generación térmica (GT) y de generación hidráulica (GH) se encuentran en la tabla 11, a continuación:
En ninguno de los escenarios se presentó racionamiento. La hidrología se modeló usando una función de distribución para cada una de las centrales hidráulicas, sin embargo, se computan los resultadosdel valor promedio del vertimiento total durante el año, en cada iteración. El vertimiento estuvo en rangos entre los 338,50 y los 1.848,7 [Hm³]. Los valores de mayor frecuencia de los vertimientos están entre 900 y 1000 [Hm³].
Conclusiones
Se construyó un modelo que resuelve efectivamente el problema de despacho hidrotérmico considerando el efecto aleatorio de las afluencias de los embalses y de la velocidad del viento, utilizando simulación de Monte Carlo, lo que facilita la toma de decisiones, puesto que plantea escenarios más ajustados a la realidad estocástica de las variables involucradas en el problema.
El costo de la energía,sin incluir el efecto de la generación eólica, y con afluencias determinísticas presentadas en tabla 4, es de 1.787.100. No se presenta racionamiento en ninguno de los embalses, y para ninguno de los períodos.
Al agregar el efecto estocástico tanto del viento como de la hidrología, el costo para cada caso de penetración eólica, esto es, 100MW, 200 MW y 1000 MW,se obtuvo una reducción en el costo de la energía que en cada caso fue de 31,73% 33,97% y 47,68%, respectivamente.
Reconocimientos
Los autores agradecen el aporte en el tema de probabilidad y estadística del Ingeniero César Augusto Peñuela de la Universidad Tecnológica de Pereira.
Referencias
1. J. Galvis, A. Garcés, A. Escobar. ''Aplicación del algoritmo de búsqueda tabú al problema de despacho hidrotérmico''. Scientia et Technica. Vol. 29. 2005. pp. 25-30. [ Links ]
2. R. Cypser. ''Computer search for economical operation of a hydrothermal electric system''. Power Apparatus and Systems, Part III. Transactions of the American Institute of Electrical Engineers. Vol. 73. 1954. pp. 1260-1267. [ Links ]
3. L. Söder. ''Reserve margin planning in a wind-hydrothermal power system''. Power Systems, IEEE. Vol. 8. 1993. pp. 564-571. [ Links ]
4. R. de Aquino, M. Lira, J. de Oliveira, M. Carvalho, O. Neto, G. Almeida. Application of wavelet and neural network models for wind speed and power generation forecasting in a Brazilian experimental wind park. Proceedings of the International Joint Conference Neural Networks. Georgia, USA. 2009. pp. 172-178. [ Links ]
5. H. Chen, J. Wang, Y. Zhang. Economic Dispatch of Hydro-Thermal Power System with Large-Scale Wind Power Penetration. Proceedings of the Power and Energy Engineering Conference (APPEEC), Asia- Pacific. Shangai, China. 2012. pp. 1-29. [ Links ]
6. B. Gorenstin, N. Campodonico, J. Costa, M. Pereira. ''Stochastic optimization of a hydrothermal systema using network constrains''. IEEE. Vol. 7. 1992. pp. 497-501. [ Links ]
7. S. Soares, C. Lyra, H. Tavares. ''Optimal Generation Scheduling for Hydrothermal Power Systems''. IEEE Transactions on Power Apparatus and Systems. Vol. PAS-99. 1980. pp. 1107-1118. [ Links ]
8. R. Jiménez, V. Paucar. Long term hydrothermal scheduling linear programming model for large scale power systems. Proceedings of the Large Engineering Systems Conference, Power Engineering. Montreal, Canada. 2007. pp. 96-100. [ Links ]
9. R. Karki, P. Hu, R. Billinton. Reliability assessment of a wind integrated hydro-thermal power system. Proceedings of the IEEE 11th International Conference, Probabilistic Methods Applied to Power Systems (PMAPS). Singapur, Singapur. 2010. pp. 1172-1177. [ Links ]
10. C. Sun, Z. Bie, G. Li, B. Hua. Analysis of wind power integration capacity in wind-hydro-thermal hybrid power system. Proceedings of the 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies Europe (ISGT). Berlin, Germany. 2012. pp. 1-8. [ Links ]
11. Ministerio de Minas y Energía. Atlas del viento y energía eólica de Colombia. Bogotá, Colombia. 2006. pp. 7, 146. [ Links ]
12. Ministerio de Minas y Energía, UPME. Plan de expansión de referencia. Generación-Transmisión, 2009-2023. Bogotá, Colombia. 2009. pp. 23. [ Links ]
13. EPM. Parque Eólico Jepirachi. Available on: http://www.epm.com.co/site/Home/Institucional/Nuestrasplantas/Energía/ParqueEólico.aspx. Accessed: June 15, 2013. [ Links ]
14. W. Sifuentes, A. Vargas. ''Hydrothermal Scheduling Using Benders Decomposition: Accelerating Techniques''. Power Systems, IEEE. Vol. 22. 2007. pp. 1351-1359. [ Links ]
15. A. Helseth, G. Warland, B. Mo. Long-term hydrothermal scheduling including network constraints. Proceedings of the 7th International Conference on the European Energy Market (EEM). Madrid, Spain. 2010. pp. 1-6. [ Links ]
16. C. Yasar, S. Fadil. Solution to lossy short-term hydrothermal coordination problem with limited energy supply thermal units by using first order gradient method. Proceedings of the International Conference on Electrical and Electronics Engineering (ELECO). Bursa, Turkey. 2009. pp. 129-133. [ Links ]
17. D. Legalov, S. Palamarchuk. Hydro generation scheduling with electricity price calculation. Proceedings of the IEEE Power Tech Conference. St. Petersburg, Rusia. 2005. pp. 1-6. [ Links ]
18. X. Bai, S. Shahidehpour. ''Hydrothermal scheduling by tabu search and decomposition method''. IEEE Transactions on Power Systems. Vol. 11. 1996.pp. 968-974. [ Links ]
19. D. Mejía, J. Franco, R. Gallego. ''Solución al problema del despacho de energía en sistemas hidrotérmicos usando simulated annealing''. Scientia et Technica. Vol. 29. 2005. pp. 7-12. [ Links ]
20. J. Zhang, J. Wang, C. Yue. ''Small Population- Based Particle Swarm Optimization for Short-Term Hydrothermal Scheduling''. Power Systems, IEEE. Vol. 27. 2012. pp. 142-152. [ Links ]
21. D. Mejía. Coordinación hidrotérmica de sistemas eléctricos usando predicción de caudales afluentes. Tesis de maestría en Ingeniería Eléctrica. Universidad Tecnológica de Pereira. Pereira, Colombia. 2005. pp. 48-99. [ Links ]
22. ILOG. IBM log AMPL Version 12.2 User's Guide. Available on: http://www.ampl.com/BOOKLETS/amplcplex122userguide.pdf. Accessed: July 8, 2014. [ Links ]
23. L. Escobar, A. Duque, J. Melchor, A. Escobar. ''Planeamiento de sistemas de transmisión de energía eléctrica usando AMPL''. Scientia et Technica. Vol. 51. 2012. pp. 42-50. [ Links ]
24. I. Isaac, J. Areiza, J. González, H. Biechl. Long-term energetic analysis for electric expansion planning under high wind power penetration scenarios in Colombia and neighboring countries. Proceedings of the 7th International Conference on the European, Energy Market (EEM). Madrid, Spain. 2010. pp. 1-7. [ Links ]
25. J. Manwell, J. McGowan, A. Rogers. Wind Energy Explained. Theory, design and application. 1st ed. Ed. John Wiley & Sons, Ltd. 2002. Chichester, England. pp. 57-59. [ Links ]
26. M. Patel. Wind and solar power systems. 11st ed. Ed. CRC Press LLC. New York, USA. 1999. pp. 52-54. [ Links ]
27. Ministerio de Minas y Energía, UPME. Sistema de información eléctrico colombiano. Demanda máxima de potencia mensual 2013. Available on: http://www.upme.gov.co/GeneradorConsultas/Consulta_Indicador.aspx?IdModulo=2&ind=3. Accessed: June 27, 2013. [ Links ]
28. ISA. Dirección planeación de la operación gerencia Centro Nacional de Despacho. Documento ISA UENCND 04-053. 2004. p. 6. [ Links ]
29. G. Canavos. Probabilidad y estadística. Aplicaciones y métodos. 2nd ed. Ed. Mc Graw-Hill. México D.F., México. 1988. pp. 130-159. [ Links ]
30. A. Garcés, O. Gómez. ''Solución del problema del despacho hidrotérmico mediante simulación de Monte Carlo y punto interior''. Revista Facultad de Ingeniería Universidad de Antioquia. Vol. 45. 2008. pp. 132-147. [ Links ]
31. Ministerio de Minas y Energía, UPME. Proyección de demanda de energía eléctrica en Colombia. Bogotá, Colombia. 2013. Available on: http://www.siel.gov.co/siel/documentos/documentacion/Demanda/proyeccion_demanda_ee_Abr_2013.pdf. Accessed: June 20, 2013. [ Links ]




























