ARTÍCULO ORIGINAL

DOI: 10.17533/udea.redin.n75a16

Simulating gas-liquid mass transfer in a spin filter bioreactor

Simulación de la transferencia de masa en un biorreactor de perfusión operado con un filtro rotativo

Lilibeth Caridad Niño-López, Germán Ricardo Gelves-Zambrano*

Grupo de Bioprocesos, Departamento de Ingeniería Química, Universidad de Antioquia. Carrera 53 N.° 61-30. Medellín, Colombia.

* Corresponding author: Germán Ricardo Gelves Zambrano, e-mail: german.gelves@udea.edu.co

(Received July 30, 2014; accepted March 17, 2015)

Abstract

Computational fluid dynamics (CFD) and population balance model (PBM) model have been used to simulate hydrodynamics and mass transfer in a 0.014 m³ Spin Filter Bioreactor. The operating conditions chosen were defined by typical settings used for culturing plant cells. Turbulence, rotating flow, bubbles breakage and coalescence were simulated by using the k-e, MRF (Multiple Reference Frame) and PBM approaches, respectively. The numerical results from different operational conditions are compared with experimental data obtained from k_La measurements and good fitting data is achieved. Interested by these simulated and experimental results CFD simulations are qualified as a very promising tool not only for predicting gas-liquid hydrodynamics but also for finding design requirements that must be implemented to optimize an aerobic bioprocessing useful for plant cell culture applications which are characterized by the constrain of achieving relatively high mass transfer conditions and avoiding cellular damage due to hydrodynamic conditions.

Keywords: bioreactor, scale up, multiple reference frame (MRF), population balance model (PBM), spin filter

Resumen

Mediante dinámica de fluidos computacional (CFD) y métodos de balance poblacional (PBM) se simuló la hidrodinámica líquido-gaseosa y la transferencia de masa en un biorreactor de 0,014 m³ operado con un Spin Filter para cultivos en modo perfusión. Las condiciones de operación fueron definidas con base en los requerimientos para células vegetales en suspensión. Los fenómenos de turbulencia, flujo giratorio, ruptura y coalescencia de burbujas fueron simulados utilizando los modelos k-e, MRF (Multiple Reference Frame) y PBM. Se logra una predicción aceptable mediante la comparación entre los resultados numéricos de las diferentes condiciones de operación y los datos experimentales de los valores del coeficiente de transferencia de masa k_La. Con la motivación de estos resultados simulados y validados experimentalmente, se observa que CFD puede ser una herramienta muy prometedora, no sólo para la predicción de la hidrodinámica líquido-gaseosa, sino también para encontrar los requisitos de diseño que se deben implementar para optimizar un proceso biológico aerobio útil para aplicaciones de cultivos celulares de plantas, que son comúnmente caracterizados por el requerimiento de mantener condiciones relativamente altas tasa de transferencia de masa y simultáneamente evitar el daño celular debido a las condiciones hidrodinámicas.

Palabras clave: biorreactor, escalado, marco de referencia múltiple, método de balance poblacional, filtro rotativo

Introduction

Global productivity in large scale processes depends on gas-liquid conditions. Supplying adequate oxygen levels in aerobic cell culturing is a common problem in fermentation technology. This problem is increased in high cell density bioreactors due to oxygen transfer rate limitations affecting cell growth and productivity. Such limitations are common in perfusion cell cultures leading to anoxic process, cellular damage and therefore loss of cell viability [1].

Perfusion technology is used for increasing the productivity of such compounds. One of the most common devices for perfusion processes is the Spin-Filter, which is used for animal and plant cell cultures in continuous production processes. Such bioreactors incorporate a rotating filter device into a stirred tank reactor. Cells are inoculated and cultivated by continuous addition of fresh nutrient medium. The spin-filter device minimizes the loss of cells through the bioreactor harvest. Consequently biomass productivity is increased substantially compared to batch or fed batch mode [1]. However oxygen requirements are proportional to cell density causing mass transfer limitations. There has been rapid progress in the modeling of large-scale performance by the application of computational fluid dynamics (CFD). Successful examples are given covering the range from agitation systems, including models from single phase rotating impeller systems [2-6] to the use of population balance models [7-14]. The main purpose of these approaches is the knowledge of the flow fields in conventional stirred tanks (hydrodynamics) related to mass transfer profiles.

Spin-filters (SF) were proposed as cell retention devices for animal cell culture several decades ago [15] and became a popular device for perfusion cultivations both for small-scale studies and large-scale processes [16-18].

Although several works have dealt with the understanding flow field and particle dynamics of these devices, gas-liquid mass transfer phenomena and hydrodynamics has not yet been studied. To the authors knowledge CFD simulations for gas-liquid hydrodynamics in Spin Filter Bioreactor had never been used previously for evaluating mass transfer prediction. For this reason detailed understanding of hydrodynamic behavior can be useful not only for identifying mass transfer limitations but also for finding design requirements that must be implemented to optimize an aerobic bioprocessing. Hence it is the motivation of this work to simulate gas-liquid hydrodynamics in a Spin Filter bioreactor using a CFD approach for mass transfer.

Materials and methods

Bioreactor setup

A Spin Filter stirred tank bioreactor (New Brunswick Celligen 310) with 0.008 m³ working volume (T = 0.21 m) was used in this study. The mixing is driven by a conventional Pitched Blade Impeller (D = 0.1 m) mounted on a 0.02 m diameter shaft and placed at the center line of the bioreactor. The gas is supplied through a 0.02 m diameter cylinder micro-sparger. The operating conditions chosen were defined by typical settings used for culturing plant cells: N_i = 70, 140 and 210 rpm, aeration rate = 0.04 vvm. The properties used in the primary phase (water) are: ρ_L: 998.2 kgm⁻³; μ_L: 0.001 kgm⁻¹ s⁻¹. σ: 0.07 Nm⁻¹. Secondary phase properties (air) are: ρ_G: 1.225 kgm⁻³, μ_G = 1.789 10⁻⁵ kgm⁻¹ s⁻¹ [19].

Computational Fluid Dynamic Model

Multiphase Flow Equations

The gas and liquid phase are treated as interpenetrating continua and conservation of mass and momentum equations are solved for each phase. The conservation equations for each phase are derived to obtain a set of equations, which have similar structure for all phases [13, 20-25].

The Eulerian model is the most complex multiphase model in ANSYS FLUENT 13.0. It solves a system of n-momentum and continuity equations for each phase. The coupling is achieved through pressure and interfacial exchange coefficients. The mass conservation equation for each phase is shown (Eq. 1):

Where ρ_i, represent the density, volume fraction and mean velocity, respectively, of phase i (L or G). It is assumed that the liquid phase and the gaseous phase share space proportional to their volume, such that their volume fractions sum up to unity in the cell domain (Eq. 2):

The momentum equation for phase i is described below (Eq. 3):

P is the pressure shared by both phases and represents the interfacial momentum exchange. The term represents the Coriolis and centrifugal forces expressed in the MRF (Multiple Reference Frame) model for rotating flows and is represented as (Eq. 4):

is the angular velocity, is the position vector. The Reynolds stress tensor (Eq. 5) is related to the mean velocity gradients through the Boussinesq hypothesis [20]:

is the molecular viscosity of phase i, , is the strain tensor.

Interfacial Momentum Exchange

The most important interphase force is the drag force acting on the bubbles. This force (Eq. 6) depends on friction, pressure, cohesion, and other hydrodynamic effects [26].

K is the exchange coefficient of liquid and gaseous phases and is determined by (Eq. 7):

d is the bubble diameter, and the drag coefficient C_D is defined as a function of Reynolds number (Eq. 8):

To calculate the drag coefficient the standard correlation [27] was applied (Eq. 9):

Equations for the turbulence model

The dispersed turbulence k - ε model can be considered as the multiphase standard turbulence approach. It represents the extension of the single phase k - ε model and is used when the secondary phase concentrations are diluted on primary phase. k and ε equations describing this model are as follows (Eqs. 10 and 11):

In these equations, G_k,L represents the generation of turbulent kinetic energy, k_L of the liquid phase due to mean velocity gradients, ε_L is the turbulent dissipation energy. Π_K,L and Π_ε,L represent the influence of the dispersed phase in the continuous phase, respectively [28].

The turbulent viscosity μ_t,L, is calculated from (Eq. 12):

The values of the constants used in this experiment were C_1ε: 1.44, C_2ε: 1.92, C_μ: 0.09, σ_k: 1.00 and σ_ε: 1.30. σ_k and σ_ε represent turbulent Prandtl number for k and ε, respectively [28].

Population balance model for bubble distributions

The discrete method [29-31] is used herein to solve the population balance equations. The bubble population is discretized into a finite number of intervals of bubble diameters. The population balance equations (Eq. 13) for different bubble classes can be written as [32-34]:

Where n_i is the number of bubbles per class i , Γ_BiC and Γ_BiB are birth rates due to coalescence and breakage, respectively, Γ_DiC and Γ_DiB are the death rates.

The terms of breakage and coalescence are (Eqs. 14-17):

a(v,v') is the coalescence rate between bubbles of size v and v'; g(v) is the breakup rate of bubbles of size v; g(v'), is the breakup frequency of bubble v' and β(v│v') is the probability density function of bubbles broken from the volume v' in a bubble of volume v.

The bubble breakup is analyzed in terms of bubbles interaction with turbulent eddies. These turbulent eddies increase the bubble surface energy to cause deformation. The breakup occurs if the increase in the surface energy reaches a critical value. The break up rate (Eqs. 18-20) is defined as [3]:

Where d is the bubble diameter, ξ is the dimensionless eddy size, f is the breakage frequency. The bubble coalescence is modeled by considering the bubble collision due to turbulence, buoyancy and laminar shear. The coalescence rate (Eq. 21) is defined as the product of the collision frequency ω_ag(v_i, v_j) and coalescence probability P_ag(v_i , v_j) and is defined as [3]:

The collision frequency is defined as (Eq. 22):

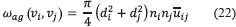
Where u̅_ij is the characteristic collision velocity of two bubbles with diameter d_i and d_j and bubble density n_i and n_j (Eq. 23):

Where c₁ is a first order constant, x_ij=d_i /d_j ρ₁ and ρ₂ the densities of primary and secondary phase.

The number of bubbles per class i, n_i is related to the gas phase volume fraction as follows (Eq. 24):

The sum of the volume fractions of each group of bubbles is equal to the volume fraction of the dispersed phase (Eq. 25):

The volume fraction of each group sizes is expressed in terms of the total fraction of the dispersed phase (Eq. 26):

Therefore, including Eq. (26) in Eq. (13), is (Eq. 27):

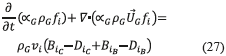
The Sauter diameter d₃₂ is used to fit the population balance equations with the bioreactor hydrodynamics (Eq. 28):

Mesh processing and numerical technique

A fine 3D mesh (Figure 1) is composed for tetrahedral cells with 1000 computational k cells for the Spin Filter Bioreactor.

The finite volume technique implemented in the CFD code Ansys Fluent 13.0 Software was used to convert the Navier- Stokes equations into algebraic equations which can be solved numerically. Tank walls, stirrer surfaces and baffles are treated with no slip conditions and standard wall functions.

The gas flow rate at the cylinder micro-sparger was defined via inlet-velocity type boundary condition with gas volume fraction equal to unity. MRF model was applied for the impeller (Pitched Blade) and Spin Filter device. PC SIMPLE algorithm was used for solving the partial differential equations. The second order upwind scheme was applied for the spatial terms. It was assumed that the solution converges when the scaled residuals remain with values smaller than 10^-5 and when the pseudo-regime for hold-up is reached [9, 10]. The size of the bubbles was set by the discretization scheme based on the geometric ratio [9]. The size of the bubbles for the Spin Filter Bioreactor was assumed from 75 to 2000 µm in diameter. 13 size classes were used to discretize the population balance equations [10], who analyzed hydrodynamics of a propeller type stirrer and found satisfactory results using the same classifiers. Power input P (Eq. 29) is calculated using torque M of the impeller (in Ansys fluent called the Moment Center) [7]:

Experimental k_La measurements

Experimental k_La measurements were performed applying the N₂-stripping approach in aqueous medium. Time courses of increasing dissolved oxygen levels were monitored via an O₂-probe (Mettler Toledo, Germany). k_La estimations (Eq. 30) resulted from non-linear parameter fitting using equation [13]:

with i coding for subsequent time points t and * indicating the saturating dissolved oxygen levels C_O2. Time series of dissolved oxygen were corrected with respect to the delayed probe responses which had been identified as ~28 seconds, relating to τ=0.035 [1/s].

Results

The main propose of this work was to study the gas-liquid mass transfer hydrodynamics using a Spin Filter bioreactor. For that reason detailed understanding of hydrodynamic behavior can be useful not only for identifying mass transfer limitations but also for finding design requirements that must be implemented to optimize an aerobic bioprocessing. The simulated operating conditions are based on typical values of plant cell cultivations. Special emphasis was given to the evaluation of local k_La distributions. Figure 2 shows the CFD air volume fractions of the Spin Filter bioreactor operated at different impeller speed. It can be seen that relatively low air dispersion occurs in the bioreactor when it was operated at 70 rpm. Poor air volume fractions are caused by low centrifugal forces. Obviously, these centrifugal forces could not overcome the air buoyancy [13]. Contrary, air gradients are minimized when the stirrer tank is operated at 140 and 210 rpm.

Figure 3 shows the velocity vectors calculated for the Spin Filter bioreactor operated at: (a) 70 rpm, (b) 140 rpm and (c) 210 rpm. Similar results were demonstrated in all cases. The pitched blade geometry and bottom Spin filter surface pump the fluid slightly downwards around the impeller discharge region. Consequently, high k_La mass transfer regions were generated in all the operating conditions tested by CFD. Noteworthy, similar results were found by [13] who compared the gas–liquid hydrodynamics of a Rushton turbine with a new pitched blade impeller. It is observed that highest velocities are found in striking distance to the rotating Pitched Blade and Spin Filter. Moreover, the mean velocity decreases gradually away from the Impeller and becomes very low at the bottom and at the top of the bioreactor.

In aerobic fermentations, air flows continuously through the stirred tank reactor. The bubble size distribution results from physical interactions imposed on uprising bubbles and considers mechanisms such as coalescence and breakage. These phenomena together with hydrodynamics, trigger the formation of dissolved oxygen and trace gases gradients of which can affect productivity in aerobic plant cell cultures. For that reason, when breakage phenomenon prevails, bubble size decreases, the interfacial area for mass transfer thereof is increased and consequently, the oxygen transfer is promoted. On the other hand, large bubbles generated by coalescence are characterized by higher rising velocities and short residence times. Thereby, bubbles cannot be uniformly dispersed for the agitation system. The most relevant parameter for analyzing these hydrodynamic mechanisms is the Sauter mean diameter. It can be interpreted as an integral parameter, summarizing all individual impacts affecting the bubble sizes and their distribution in one single value [13]. It is estimated from CFD-based hydrodynamics and population balance models.

Figure 4 shows the Sauter mean diameter contours of the Spin Filter bioreactor operated at different impeller speeds: (a) 70 rpm, (b) 140 rpm and (c) 210 rpm. Interestingly, lowest values of 5e-4 m were found when Spin Filter was operated at 210 rpm. These small Sauter diameters were dispersed homogeneously when relatively high local bubble breakage and downward pumping rates take place. This finding is in agreement with reports of [10], who analyzed hydrodynamics of a propeller type stirrer. Largest mean Sauter diameters of 9 e-4 m were simulated when 70 rpm was used as stirring velocity. These coalescing zones are caused by low mixing. Considering simulated mass transfer, these zones are candidates for poor oxygen mass transfer levels.

Therefore, this result shows that 70 rpm is not a good operational condition for the Spin Filter because of its low power input (0.03 W) can generate poor mixing and undesired large buble sizes. Still, 210 rpm seems to be the best parameter for the Spin Filter device in terms of Sauter diameter, but the high power input required (0.77 W) can be a disadvantage in large scale prototypes. Based on this information, a new prototype of bioreactor should be designed to disperse average bubble sizes of 5e-4 m but it is important to bear in mind the constrain of avoiding large power input requirements. However, the cell damage theory of Kolmogorov suggests that any biological entity will damage if its size is greather than the Kolmogorov diameter scale [14]. Figure 5 shows that Kolmogorov diameters were calculated as 140, 70 and 45 µm for 70, 140 and 210 rpm, respectively. Considering that average size of a plant cell is 50 µm, cell damage should be expected if the Spin Filter device is operated at 210 rpm. Interestingly, acceptable gas-liquid hydrodynamics were found by reducing 69 % the impeller power input (0.23 W) when CFD simulations were performed at 140 rpm. In terms of saving energy and cellular constraints, 170 rpm proved to be the best operational condition.

Maintaining an adequate oxygen supply to aerobic cell cultures has been a long-standing problem in fermentation technology. This problem is particularly amplified in high cell density cultures, in which insufficient oxygen transfer rates limit cell growth and ultimately process productivity [35].

k_La values (Figure 6) are considered as the principal criterion to analyze the gas/liquid mass transfer. In this work, Higbies' penetration theory is used for simulating k_La from CFD. These values are obtained by the product of liquid mass transfer k_La and interfacial area k_La [34]. Interfacial area is expressed as a function of the local gas fraction and the local Sauter diameter.

Given the biochemical constraint that cell cultivations require optimum dissolved oxygen levels for growth ensuring a minimum of 5 % (at atmospheric conditions) [36], sufficient oxygen transfer rates are obviously only achieved if k_La values reach fairly high levels [13]. Simulating the Spin Filter Bioreactor, oxygen mass transfer, expressed by k_La (Figure 6), was found to be about 3 times higher with 210 rpm than values obtained at 70 rpm. At the given operational conditions (70 rpm), the Spin Filter system reached only an integral k_La of 18.0 1/h while increasing the power input the k_La values attained 33.2 and 60.0 1/h at 140 and 210 rpm, respectively. The latter is the consequence of the improved gas-liquid mass transfer which ensures the formation of uniform bubble sizes, generally caused by the hydrodynamics. In terms of saving energy and cellular constraints, 170 rpm remained to be the best operating condition for the Spin Filter bioreactor.

Moreover, experimental k_La measurements were tested using the operating conditions of the CFD simulations. Experimental tests showed k_La values of 20.0, 35.1 and 63.3 1/h for 70, 140 and 210 rpm, respectively, that fit very well to the simulations. The very good agreement is qualified as a proving for the accurate of coupling of the population balance models and gas-liquid hydrodynamics terms used in CFD.

Conclusions

Numerical results from gas-liquid mass transfer in a Spin Filter Bioreactor are analyzed using CFD. Comparing CFD simulations with experimental k_La measurements show that good agreement is achieved. Motivated by these simulated and experimental results CFD simulations are qualified as a very promising not only for predicting gas-liquid hydrodynamics but also for finding design requirements that must be implemented to optimize an aerobic bioprocessing especially useful for plant cell culture applications which are characterized by the constrain of achieving relatively high mass transfer conditions and avoiding cellular damage due to hydrodynamic conditions. Gas-liquid mass transfer, bubble size diameter and Kolmogorov lenght scales can be treated as main criteria for desingning a new stirred tank bioreactor applied to plant cell cultures.

Acknowledgments

The authors gratefully acknowledge to Professor Lucía Atehortúa and CODI (Committee for Research Development of the Universidad de Antioquia).

References

1. S. Sens, P. Roychoudhury. ''Step-up/step-down perfusion approach for increased mAb 520C9 production by a hybridoma cell line''. Biotechnol Lett. Vol. 35. 2013. pp. 153-163.         [ Links ]

2. M. Jenne, M. Reuss. ''A critical assessment on the use of k–e turbulence models for simulation of the turbulent liquid flow induced by Rushton turbine in baffled stirred-tank reactors''. Chem Eng Sci. Vol. 54. 1999. pp. 3921-3941.         [ Links ]

3. J. Luo, R. Issa, A. Gosman. ''Prediction of impeller induced flows in mixing vessels using multiple frames of reference''. Inst. Chem. Eng. Symposium Series. Vol. 136. 1994. pp. 549-556.         [ Links ]

4. G. Micale, F. Grisafi. ''Prediction of flow fields in a dual-impeller stirred tank''. AICHE J. Vol. 45. 1999. pp. 445-464.         [ Links ]

5. K. Rutherford, C. Lee, S. Mahmoudi, M. Yianneskis. ''Hydrodynamic characteristics of dual Rushton impeller stirred vessels''. AICHE J. Vol. 42. 1996. pp. 332-346.         [ Links ]

6. A. Tabor, G. Gosman, R. Issa. ''Numerical simulation of the flow in a mixing vessel stirred by a Rushton Turbine''. Inst. Chem. Eng. Symposium Series. Vol. 140. 1996. pp. 25-34.         [ Links ]

7. V. Bakker, V. Akker. ''A computational model for the gas–liquid flow in stirred reactors''. Transactions of the Institution of Chemical Engineers. Vol. 72. 1994. pp. 594-606.         [ Links ]

8. F. Kerdouss, A. Bannari, P. Proulx, R. Bannari, M. Skrga, Y. Labrecque. ''Two-phase mass transfer coefficient prediction in stirred vessel with a CFD model''. Comput and Chem Eng. Vol. 32. 2008. pp. 1943-1955.         [ Links ]

9. F. Kerdouss, L. Kiss, P. Proulx, J. Bilodeau, C. Dupuis. ''Mixing characteristics of an axial flow rotor: Experimental and numerical study''. Int J of Chem React Eng. Vol. 3. 2005. pp. 35.         [ Links ]

10. F. Kerdouss, A. Bannari, P. Proulx, R. Bannari, M. Skrga, Y. Labrecque. ''Two-phase mass transfer coefficient prediction in stirred vessel with a CFD model''. Comput and Chem Eng. Vol. 3. 2007. pp. 1-13.         [ Links ]

11. G. Lane, M. Schwarz, G. Evans. ''Numerical modeling of gas–liquid flow in stirred tank''. Chem Eng Sci. Vol. 60. 2005. pp. 2203-2214.         [ Links ]

12. C. Venneker, V. Derksen. ''Population balance modeling of aerated stirred vessels based on CFD''. AICHE J. Vol. 48. 2002. pp. 673-684.         [ Links ]

13. R. Gelves, A. Dietrich, R. Takors. ''Modeling of gas-liquid mass transfer in a stirred tank bioreactor agitated by a rushton turbine or a new pitched blade impeller''. Bioprocess and Biosystem Engineering. Vol. 37. 2014. pp. 365-375.         [ Links ]

14. Y. Deo, M. Mahadevan, R. Fuchs. ''Practical Considerations in Operation and Scale-up of Spin-Filter Based Bioreactors for Monoclonal Antibody Production''. Biotechnol Prog. Vol. 12. 1996. pp. 57-64.         [ Links ]

15. P. Himmelfarb, P. Thayer, H. Martin. ''Spin-filter culture: The propagation of mammalian cells in suspension''. Science. Vol. 164. 1969. pp. 555-557.         [ Links ]

16. L. Castilho, R. Medronho. ''Cell retention devices for suspended-cell perfusion cultures''. Adv Biochem Eng Biotechnol. Vol. 74. 2002. pp. 129-169.         [ Links ]

17. L. Chu, D. Robinson. ''Industrial choices for protein production by large-scale cell culture''. Curr Opin Biotechnol. Vol. 12. 2001. pp. 180-187.         [ Links ]

18. A. Figueredo, J. Navarrete, P. Vitón, E. Martínez, A. Castro, E. Chico. ''Effect of different variables on the long-term spinfilter clogging during pilot-scale animal cell perfusion runs''. F. Gòdia, M. Fussenegger (editors). Animal cell technology meets genomics. Vol. 2. Ed. Springer. Dordrecht, Netherlands. 2005. pp. 683-685.         [ Links ]

19. D. Lide. CRC Handbook of Chemistry and Physics. 83^rd ed. Ed. CRC Press. 2002. Boca Raton, USA. pp. 8-232.         [ Links ]

20. G. Kasat, A. Pandit, V. Ranade. ''CFD Simulation of Gas-Liquid Flows in a Reactor Stirred by Dual Rushton Turbines''. Int J of Chem React Eng. Vol. 6. 2008. pp. 1-28.         [ Links ]

21. L. Wei. Multiple Impeller Gas-Liquid Contactors. Technical report, National Taiwan University. Taipei, Taiwan. 2004. pp. 13-47.         [ Links ]

22. V. Ranade, J. Dommeti. ''Computational Snapshot of flow generated by axial impellers in baffled stirred vessels''. J. Chem. Vol. 74. 1990. pp. 476-484.         [ Links ]

23. V. Ranade. Computational Flow Modeling for Chemical Reactor Engineering, Process Systems Engineering Series. 1^st ed. Ed. Academic Press. New York, USA. 2002. pp. 35-54.         [ Links ]

25. E. Marshall, A. Bakker. Computational fluid mixing. Technical report. Ed. Fluent-Inc. Lebanon, USA. 2002. pp. 1-94.         [ Links ]

26 R. Gelves, A. Benavides, J. Quintero. ''Predicción del comportamiento hidrodinámico en el escalado de un reactor de tanque agitado para procesos aerobios, mediante CFD''. Ingeniare. Rev. chil. ing. Vol. 21. 2013. pp. 347-361.         [ Links ]

27. M. Ishii, N. Zuber. ''Drag coefficient and relative velocity in bubbly, droplet or particulate flows''. AIChE J. Vol. 25. 1979. pp. 843-855.         [ Links ]

28. S. Elgobashi, M. Rizk. ''A two-equation turbulence model for dispersed dilute confined two-phase flows''. Int J of Multiph Flow. Vol. 15. 1989. pp. 119-133.         [ Links ]

29. M. Hounslow, R. Ryall, V. Marschall. ''A Discretized Population Balance for Nucleation, Growth and Aggregation''. AIChE J. Vol. 34. 1988. pp. 1821-1832.         [ Links ]

30. J. Litster, D. Smit, M. Hounslow. ''Adjustable Discretization Population Balance for Growth and Aggregation''. AIChE J. Vol. 41. 1995. pp. 591-603.         [ Links ]

31. D. Ramkrishna. Population Balances: Theory and Applications to Particulate Systems in Engineering. 1^st ed. Ed. Academic Press. New York, USA. 2000. pp. 47-116.         [ Links ]

32. P. Chen, M. Dudukovic, J. Sanyal. ''Numerical simulation of bubble columns flows: effect of different breakup and coalescence closures''. Chem Eng Sci. Vol. 60. 2005. 1085-1101.         [ Links ]

33. L. Hagesaether, H. Jakobsen, A. Hjarbo, H. Svendsen. ''A coalescence and breakup module for implementation in CFD-codes''. European Symposium on Computer Aided Process Engineering. Vol. 8. 2000. pp. 367-372.         [ Links ]

34. J. Sanyal, D. Marchisio, R. Fox, K. Dhanasekharan. ''On the comparison between population balance models for CFD simulation of bubble columns''. Ind Eng and Chem Res. Vol. 44. 2005. pp. 5063-5072.         [ Links ]

35. B. Pocurull. Mechanistic modeling of increased oxygen transport using functionalized magnetic fluids in bioreactors. PhD Thesis, Massachusetts Institute of Technology. Cambridge, USA. 2005. pp. 1-180.         [ Links ]

36. S. Oh, A. Nienow, M. Al-Rubeai, A. Emery. ''The effects of agitation intensity with and without continuous sparging on the growth and antibody production of hybridoma cells''. J of Biotechnol. Vol. 12. 1989. pp. 45-61.         [ Links ]