1. Introduction

Picking operation is one the most important operations performed in a warehouse due to its impact on costs and customer satisfaction [1, 2]. The costs are usually higher in manual rather than automated order-picking systems since manual picking is labour intensive and requires material-handling equipment such as forklifts, pallet jacks, etc. [3].

A refrigerated warehouse is a logistics centre that is planned, executed and controlled with the aim of maintaining the cold chain of different kinds of products, preserving their quality and physical characteristics [4]. Picking operation in a refrigerated warehouse should be performed in the shortest possible timeframe due to the low temperatures of the working environment and the potential for this condition to affect the performance of workers and the material-handling equipment. For this reason, the formulation and solution of problems in this operation are of great importance, enabling the proper planning, execution and control of these activities (e.g., order batching, routing, etc.).

The papers reviewed in the scientific literature mainly covered one of two topics: order batching and picking routing problems for traditional warehouses and distribution centres. With regards to order batching problems, a General Variable Neighbourhood search algorithm in order to execute the operation in the shortest possible time was formulated and solved [5]. In addition, a novel Tabu search (TS) algorithm, integrated with a new clustering algorithm is developed to solve an order batching problem and to perform picking operations with the shortest possible distance [6]. With regard to picking routing problems, a solution for optimizing the dynamic order-picking routes is developed, which contributes to an increase in the performance of warehouses [7]. An order batching problem that is solved using a genetic algorithm to balance the workload and reduce the number of batches to be picked is presented in the scientific literature [8]. A picking routing problem that is solved using dynamic programming to pick small- and medium-size products from storage locations at a minimum distance is formulated and solved [9]. A picking routing algorithm based on ant colony optimization (ACO), which calculates sequences of minimum possible time in order to increase the efficiency of the operation is represented and solved [10]. A picking routing problem using Tabu search metaheuristics by minimizing total operation time is presented [11].

These various reviewed papers represent either one or a fleet of homogenous material handling equipment (MHE). A fleet is deemed homogeneous when it is formed by MHE with the same travel speed and maximum lift height [12, 13]. The characteristics of a fleet of MHE can affect the ability of the solutions analysed to properly solve a picking routing problem.

In reviewing this literature, we did not detect any papers tackling picking operation design or improvements in refrigerated warehouses including the representation of a fleet of homogeneous MHE. It should be noted that in refrigerated environments that have special conditions, such as storage temperature and humidity, these will have a direct impact on the picking effectiveness of the picking operation routes designed. Therefore, this operation must be executed in the shortest possible time.

For these reasons, we identified an opportunity for research formulating a picking routing problem for refrigerated warehouses (PRPHE), considering a fleet of homogeneous MHE, which is solved using a particle swarm optimization (PSO) metaheuristic and a genetic algorithm (GA). Thus, this paper aims to contribute an advance in the state of the art, as well as improving the productivity of the refrigerated warehouse.

The paper is organized as follows. Section two describes and formulates the problem. Section three presents and develops the PSO and GA metaheuristics. Section four outlines the plan of the experiment design. Section five presents our results and discussion, analysing the findings and significant contributions. Section six offers conclusions and suggestions for further research.

2. Problem description and formulation

2.1. Problem description

A refrigerated warehouse with 1000 metres of floor area is represented for our picking routing problem. This warehouse is used for storing chilled and frozen food products. Therefore, cold chambers are installed for controlling the temperature and relative humidity. The storage units are boxes and packages that contain the frozen and chilled products. The warehouse layout comprises one depot (the start and end point of the picking operation), one main aisle and four pick aisles (Figure 1).

Figure 1 Refrigerated Warehouse Layout 

The products are picked from their storage locations using a fleet of heterogeneous MHE. The fleet comprises two kinds of MHE: manual picking carts and pallet jackets. These MHE have different load capacities and travel speeds for executing the picking operation.

This is the PRPHE including the representation of a fleet of homogeneous MHE. The PRPHE is then solved using a PSO and GA. As results of this solution, a set of routes of minimum possible time is generated. Each route contains a sequence of storage locations to be visited in the shortest possible time, using an available MHE to pick the number of products requested by the customer (orders).

2.2. Problem formulation

The PRPHE considering a fleet of homogeneous MHE is represented as a mixed integer programming problem. The set of decision variables, parameters as well as indices and sets are represented below:

Indices and sets:

Parameters:

Decision variables:

Model formulation:

Model formulation is formed by an objective function and constraints. The objective function Eq. (1) aims at minimizing the average total time for the set of cold picking routes in a refrigerated warehouse. Constraint Eq. (2) controls the allocation of each product i to exactly one route c∈C. Constraint Eq. (3) ensures that the load capacity of MHE is not surpassed by the allocated products i to the route c∈C. Constraints Eq. (4) and Eq. (5) ensure that each storage location has one predecessor and successor within a cold picking route. Constraint Eq. (6) aims to avoid sub tours in the set of S storage locations in the refrigerated warehouse. Constraint Eq. (7) ensures that decision variables are binary [0,1].

(1)

(2)

(3)

(4)

(5)

(6)

(7)

3. Particle swarm optimization (PSO) and genetic algorithm (GA) for solving the PRPHE

3.1. Particle swarm optimization (PSO)

PSO is a novel metaheuristic approach based on evolutionary techniques for solving combinatorial problems in logistics, production and business landscapes, among others [14]. PSO was developed to simulate the social behaviour of systems using a population-based swarm intelligence algorithm [15]. In addition, the PSO metaheuristics are effective for solving vehicle routing problems [16].

A PSO metaheuristic is here adapted for solving the PRPHE in a finished product warehouse. This adaptation is necessary because the particles in question for the PRPHE involve discrete encoding, whereas classical PSO focuses on continuous encoding. In the PRPHE, position and velocity operators are discretely encoded and are modelled in this section. A diagram of discrete PSO is here represented to summarize the steps of this metaheuristic (

Figure 2).

Figure 2 Diagram of discrete PSO for solving the PRPHE 

The steps of discrete PSO for solving PRPHE

Step 1: Initial set of particles for PSO are stated and randomly initialized

An initial set of picking routes or CPR (cold picking routes) is generated using a priority rule that considers the availability of heterogeneous MHE, the characteristics of the chilled and frozen products to be picked and the storage locations to be visited. This initial set of particles or CPR is stated as follows in Table 1:

Table 1 Initial set of particles (cold picking routes or CPR) 

Note: K _k : Material Handling Equipment (MHE),

Ln: Storage Location and cold picking routes

The CPR is randomly generated, taking into account constraints regarding products, MHE specifications and storage systems. Each storage location belonging to each route is a particle i which has a Xi ^r Position and Vi ^r Velocity. In addition, the parameters Gbest, Pbest, X^ri Position and V^ri Velocity are initialized.

Step 2: Calculate picking time for each particle i ^r using the fitness function

For each particle i^r belonging to each route c∈C, picking times are calculated using the following Eq. (8):

(8)

Note: Min T is equivalent to the objective function represented in the problem formulation above.

In this way, the picking time is measured for each route c∈C and then summed to calculate the total picking time of the CPR. It should be noted that these picking times are measured in minutes.

Step 3: Update velocity Vi ^r and position Xi ^r

Velocity Vi ^r and position Xi ^r of each particle are updated with regard to movements executed on the search neighbourhood [17]. The best position (Pbest) Xi ^r for the next time step is measured using Eq. (9):

(9)

Where:

On the other hand, Velocity Vi ^r is calculated by Eq. (10):

(10)

Where:

A new position for a particle is calculated using the following Eq. (11):

(11)

As explained above, a discrete PSO is formulated for solving the PRPHE, as a particle (CPR) is encoded discretely. A discrete PSO generates a new position at time t+1 using a structure of movements different from classical PSO metaheuristics (¹⁵). The main difference between these PSO approaches is the velocity v operator, which comprises a list of transpositions. A transposition is an exchange of a pair of storage locations (Ln, Ln), which are successively switched on an 𝑥 𝑖 𝑟 𝑡 according to the length of the list of transpositions T.

A structure of movements applies transpositions of according to the length of the transposition, which equals two (T=2) in this example:

First step: A route belonging to CPR is randomly selected and is set as a particle. In this case, r₁ (CPR) was randomly chosen and set as particle 𝑥 𝑖 𝑟 𝑡 . An initial set of picking routes or CPR is depicted in Table 2.

Table 2 Initial set of picking routes or CPR 

Second step: A list of transpositions is formed by two velocities operators v^t+1 _ij(1) and v^t+1 _ij(2) since the length of list is 2 (T=2).

List of transpositions is calculated by Eq. (12):

(12)

Third step: (1) and (2) are implemented successively, which gives the following results on particle that are represented in Table 3:

Table 3 Velocity of particles for discrete PSO 

The three steps described above must be implemented for generating 𝑥 𝑖 𝑟 𝑡+1 for discrete PSO. In this way, this approach can be considered a contribution to the state of the art of picking, routing and warehouse.

Step 4: Evaluate if current picking time for particle i ^r ∈ ^r R is less than global Pbest

Evaluate if current picking time for particle i ∈ ^r R is less than global Pbest. If this condition is met, then Pbest is updated to the picking time of this particle i ^r ∈R. Next, evaluate if Pbest linked to the particle i ^r ∈R is less than Gbest. If this condition is also satisfied, then Gbest is updated (Gbest=Pbest).

Step 5: Stop criteria

Evaluate if Maximum iteration number or picking time planned is reached. If one of these conditions is met then PSO metaheuristic is finished and Gbest is recorded as the solution for the PRPHE.

3.2. Genetic algorithm (GA) for solving PRPHE

GA is a metaheuristic that is used for solving combinatorial problems based on natural selection, implementing mainly chromosome encoding ¹⁸. GA is implemented to execute movements for exploring feasible search spaces using encoded chromosomes ¹⁹. Crossover and mutation movements are performed within chromosomes to generate new solutions and thereby explore search spaces. Finally, GA has been an effective tool for solving picking problems in a warehouse ²⁰. A GA metaheuristic is adapted for solving the PRPHE in a finished product warehouse in this study. A diagram of the adapted GA is represented in Figure 3:

Figure 3 Diagram of GA adapted for solving the PRPHE 

3.3. Steps of GA adapted for solving the PRPHE

Step 1: Create initial population (set of picking routes)

A set of initial picking routes, or CPR, is generated using the priority rule described above. The structure of a set of initial picking routes is depicted in Table 4:

Table 4 Initial set of picking routes or CPR 

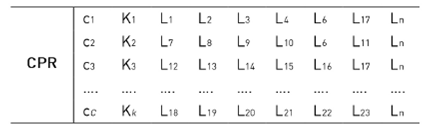
Note: This initial set of picking routes is similar to that described

above in Table 1.

Step 2: Calculate picking time of chromosomes (set of routes) using objective function

The set of CPR is evaluated by objective function for calculating the picking times, which are measured in minutes per set of routes. Objective function is represented by Eq. (13):

(13)

Note: Min T in expression (13) is equivalent to the objective function represented in the problem formulation above.

Step 3: Select operators

Ranking and tournament selection methods are implemented in the GA adapted metaheuristic. These selection methods are used to choose the best CPR generated, preserving the quality of the solutions produced by the GA metaheuristic.

Step 4: Crossover and mutation operators create new chromosomes (picking routes)

Crossover and mutation operators are used to generate new CPR (chromosome) belonging to new CPR sets. A crossover operator combines two or more parent chromosomes (solutions) to generate a new solution (CPR). The mutation operator converts movements into chromosomes.

Step 4.1: Crossover operators

Three crossover operators are developed to generate new CPR: one-point crossover, two-point crossover and uniform crossover. The one-point crossover consists of a single, randomly-selected point at which the storage locations (Ln) of two picking routes (c_C CPR) (chromosomes) are exchanged. Two-point crossover involves the selection of a pair of points between which this exchange is performed. Uniform crossover performs exchanges of pairs of storage locations (Ln) (alleles) according to swapping probability within the picking routes (chromosomes) selected. The crossover operators are represented in Figure 4.

Figure 4 Crossover operators for GA adapted for solving the PRPHE 

Sept 4.2: Mutation operators

Swap and shift moves are implemented as mutation operators. Both movements are performed within a specific picking route (chromosome) of a set of routes, unlike the crossover operator. A swap move comprises exchanging a pair of randomly-selected storage locations (Ln) within a specific picking route (c_C). A shift move consists of inserting a storage location (Ln) belonging to a picking route (c_C) at a randomly-chosen insertion point. Swap and Shift moves are depicted in Figure 5.

Figure 5 Swap and shift moves as mutation operators 

Step 5: Analyse if current picking time for new cold picking route c _C CPR is better than the current solution.

Evaluate if the current picking time for a new cold picking route c_C CPR is less than the actual route. If this condition is satisfied, then c_{C_new} is updated as the best solution for the problem.

Step 6: Stop criteria

Evaluate if the picking time planned or maximum iteration number is achieved. If one of these conditions is satisfied, then GA is stopped and the solution is recorded.

4. Experimental study

An experimental study is designed and performed to evaluate which of the represented picking factors have a significant effect on average total operation time (response variable). Depot location (F1), picking routing strategy (PSO or GA metaheuristics) (F2), number of heterogeneous MHE per group (F3) and picking list size (F4) are the factors represented in this study for the PRPHE.

We planned and performed a full factorial design involving four factors. This experimental design model was selected because restricted randomization was not detected for the experimentation. Experimental planning is depicted in Table 5:

Table 5 Experimental design for cold picking routing 

Seventy-two experimental runs were randomly performed using the computational models developed, which integrated PSO and GA metaheuristics as well as other factors represented for the PRPHE. The experimental unit was the DC (Distribution Center) presented above in our problem description. Average total picking time (variable response) was measured in minutes per set of routes (CPR).

The parameters set for the discrete PSO metaheuristic were: i) 1500 iterations, cognitive component (c₁)=0.5, ii) social component (c₂)=2, iii) (=0.7 and iv) number of iterations was 500. The parameters configured for the GA were: i) population size was 15, ii) maximum quantity of generations was 6, ii) crossover operator was a two-point crossover, iii) mutation operator was a swap moves operator, iv) selection operator was a tournament method, v) crossover probability and mutation probability were both 0.5 and vi) number of iterations was 500. The parameters were selected based on the execution of 1000 test runs. Finally, the developed metaheuristics were programmed in Java using NetBeans IDE 8.1. In addition, experiments were performed on a laptop PC with an Intel Quad Core 2.33 GHz processor and 8GB RAM.

5. Results and discussion

The results of the experiments are divided into two parts. In the first part, we present the average total cold picking times (response variable) as well as the picking factors modelled (Table 6). In the second part, an Analysis of Variance (ANOVA) table of a full factorial design with four factors is depicted and analysed (Table 7).

We implemented an empirical rule for generating cold picking routes as a benchmark for analysing the operational efficiency and average total picking times produce by the discrete PSO and GA metaheuristics. This empirical rule designed the routes using a criterion of shortest distance from the depot to the storage location to be visited to pick the frozen and chilled products. The performance or efficiency of the proposed metaheuristics was measured by the following Eq. (14):

(14)

S: Solution generated by the discrete PSO or GA metaheuristic.

B: Solution produced by the empirical rule (benchmarks). Two benchmarks were set according to PLS:

B1: Factor level combination formed by: group of 1 homogeneous MHE, centre depot, PLS of 100 products and empirical rule as routing strategy (*) (¡Error! No se encuentra el origen de la referencia.).

B2: Factor level combination formed by: group of 1 homogeneous MHE, centre depot, PLS of 250 products and empirical rule as routing strategy (**) (¡Error! No se encuentra el origen de la referencia.).

The solutions obtained for the PRPHE are represented in Table 6:

Table 6 Average total cold picking times and efficiencies obtained for the PRPHE 

The best solutions for the PRPHE were obtained using the GA metaheuristic but were closely followed by the discrete PSO, which generated an increase of operational efficiency of 82 and 83% per set of cold picking routes for a PLS of 100 and 200 products, respectively. In addition, the worst solutions were generated by the empirical rule, which demonstrates the importance of using metaheuristics for solving PRPHE and incrementing operational efficiency in the cold DC using a quantitative approach.

The experimental analysis is performed using the results of full factorial design with four factors above described. The ANOVA is depicted in Table 7:

Table 7 ANOVA table for the PRPHE 

The two-way interaction effect of the routing picking metaheuristics (RPM) by homogeneous MHE (a group of homogeneous MHE) and the main effect of picking list size (PLS) is significant at an α of 0.05. Meanwhile, depot effect is not significant. These results show than RPM has a significant impact on average total cold picking time and therefore the time difference between discrete PSO and GA metaheuristics can be analysed.

The two-way interaction effect of the RPM by homogeneous MHE is used to measure the time difference between discrete PSO and GA metaheuristics (Figure 6).

Figure 6 Two-way interaction effect plot: RPM by Homogenous MHE 

Based on this two-way interaction effect plot (

Figure 6), we can see that the GA metaheuristic produced better cold-picking routes than the discrete PSO in the three groups of homogeneous MHE represented. These results demonstrate that the GA metaheuristic generated time savings between 22.89 and 86.75 seconds per set of cold picking routes, as well as an increase of operational efficiency between 1.98 and 2.81% per set of routes. One hundred sets of cold picking routes are performed per month in the DC under investigation. Our study shows, therefore, that between 2289 and 8675 seconds could be saved per month using the GA metaheuristic. This increase in operation efficiency would account for a saving of approximately $ 125 USD per month.

The PLS main effect is used to analyse its impact on average total picking time (CRP). This interaction effect is represented in Figure 7:

Figure 7 Main effect plot: PLS 

As the PLS main effect is significant for average total picking time, this result has implications for decision-making (

Figure 7). The time difference between PLS of 100 and 200 products was of 1933 second per set of picking routes. This difference was to be expected, as the fewer products there are to be picked, the shorter the picking time. For this reason, PSL should be selected according to picking strategy and demand of products in the refrigerated warehouse. In this study, we choose a structure of 100 frozen and chilled products because this accounts for approximately 70% of the demand in the warehouse.

The depot main effect is not significant for cold picking time. Therefore, the depot is located on the left side of the DC based on a physical design criterion rather than efficiency for average total picking time.

The main finding of this experimental study is that the GA metaheuristic produced the best cold picking routes for solving the PRPHE, by contrast with the discrete PSO as shown above. The best factor level combination detected is formed by the GA metaheuristic (RPM), left side depot (Depot), picking list size (PLS) equal to 100 products and a group of five homogeneous MHE, which produced an average total picking time of 481 seconds. Two replications were executed to verify the performance of the factor level combination selected. This resulted in picking times of 475 and 495 seconds respectively, in line with the original finding. Finally, it should be noted that it is necessary to aim for the minimum possible time for cold picking operations, specifically, due to the effects of the temperature and humidity on the performance of the refrigerated warehouse. This fact justifies the selection of factor level solutions for this problem.

6. Conclusions

The picking routing problem is critical in a cold warehouse, as frozen and chilled products must be picked in the shortest possible time. Low temperatures and high rates of humidity impact on the performance of picking and others operation in a cold DC. This paper formulated and solved a picking routing problem for a refrigerated warehouse (PRPHE), which included the representation of a fleet of homogenous MHE.

Discrete particle swarm optimization (PSO) and genetic algorithm (GA) metaheuristics were developed to solve the PRPHE. Two gaps were filled by these metaheuristics. First, both metaheuristics addressed a picking routing problem in a cold DC, which had not been yet covered in the scientific literature. Second, the discrete PSO is one of the first metaheuristics published for resolving a problem in picking whose particles have a discrete structure formed by storage locations to be visited for the collection of frozen and chilled products. In the scientific literature, classical PSO is usually implemented for solving continuous problems, which is not included in the space of solutions for PRPHE.

As a result of our experimental analysis, we detected that the GA metaheuristic produced better solutions than the discrete PSO for the PRPHE. These statistical results showed that the GA metaheuristic produced time savings of between 22.89 and 86.75 seconds per set of cold picking routes, as well as an increase in operational efficiency between 1.98 and 2.81% per set of routes. Thus, it is demonstrated the yield performance of the GA metaheuristic for solving the PRPHE. Additionally, picking list size (PLS) was also detected as a significant factor in average total cold picking times. Finally, the best factor level combination detected was formed by the GA metaheuristic (RPM), left side depot (Depot), PLS equal to 100 products and a group of five homogeneous MHE, which produced an average total picking time of 481 seconds.

Further similar research representing a fleet of heterogeneous MHE and time windows, and developing other metaheuristics for PRPHE, are proposed. In this way, the ability to represent and solve cold picking routing problem in a refrigerated warehouse can be improved.