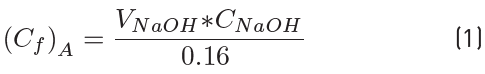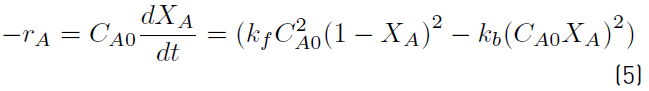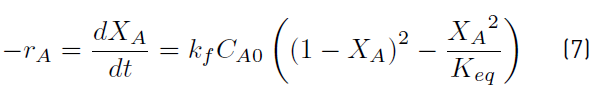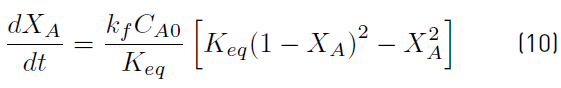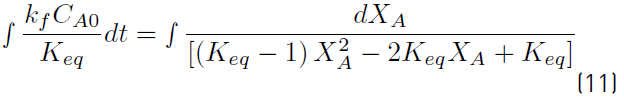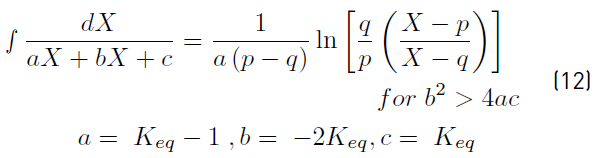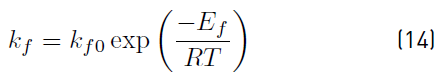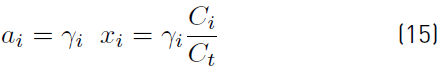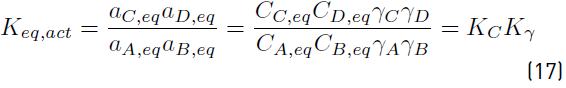1. Introduction
Esters are compounds that are widely studied due to their properties and uses in various industries such as food, fragrances, paints, fuels, among others [1,2]. The esters used in this kind of industries [3-6] are obtained from esterification of terpenols that are obtained from sources as turpentine. Nopyl acetate (6-6 - dimethylbicyclo-(3, 1,1)-2-heptene-2-ethyl acetate) is an ester that is not found in nature and it is used as a low cost alternative to linalyl acetate in a variety of perfumes and household products because of its pleasant sweet fruity-woody odor [7,8]. Currently, nopyl acetate is obtained from the Prins reaction between β-pinene (1) and paraformaldehyde (2) with a subsequent acetylation of its intermediary nopol (3) with acetic anhydride (4) at temperatures from 115°C for the catalyzed reaction with ZnCl2 to 230˚C without using catalyst, Scheme 1 [9,10].
The simplest way to produce esters with high performance is by direct esterification of acids with alcohol using homogeneous or heterogeneous catalysts [11,12]. As the esterification reactions are very slow they require typically several days to attain the equilibrium in the absence of a catalyst [13]. The esterification reactions of carboxylic acids are traditionally carried out using homogeneous catalysts, usually strong acids as HCl, HI, H3PO4 and H2SO4 [13-15]. It has been reported that although acetic acid itself may act as a catalyst, its activity for reaction is very low due to its weak acidic nature [16]. Esterification of acetic acid with ethanol in absence of catalyst yields less than 10% even at a higher temperature, which shows that the reaction is very slow and that it needs a catalyst to enhance the rate [17]. Concentrated H2SO4 catalyst is used in the industries for the esterification reactions because it is more efficient and economical than other catalysts [18]; its better catalytic activity has been attributed to its greater density of acid sites per gram [14]. H2SO4 has Brønsted-type acid sites and, is stable and liquid in (nearly) the pure form; moreover, concentrated sulfuric acid is a great dehydrating agent. As sulfuric acid is neither a strong oxidant (nitric acid) nor a strong reductant (hydroiodic acid), it reduces the possibility for undesired side reactions [19].
Liu et al. [20] reported the use of acid ionic liquids for the synthesis of terpinyl acetate with a selectivity of 87% from α-terpineol (conversion of 99%) and by esterification of α-pinene with acetic acid with a yield of 35.7% [21, 22]. Sulfonic functionalized ionic liquids (SFILs) were reported for the synthesis of terpene esters from several terpenols (geraniol, nerol, citronellol, terpinol, dihydromyrcenol) and acetic anhydride; the kinetics for SFILs in the esterification of geraniol was determined using a pseudohomogeneous model considering the main reaction and the transformation of geraniol into linalool [23]. Liquid-phase esterification of camphene was reported over silica supported H3PW12O40 producing isobornyl carboxylates with 80-90% yield [23].
For the reaction mechanism of esterification, reactions in presence of strong acids such as sulfuric acid (H2SO4), hydrochloric acid (HCl), and para-toluene sulfonic acid (p-TSA), it has been probed that the catalysts promote the protonation of the carbonyl oxygen on the carboxylic group that is then activated with nonprotonated alcohol (slowest step) to yield a tetrahedral intermediate that, by decomposition, produces the products of reaction, ester and water [13,24-27].
For acetic acid esterification with nopol using homogeneous catalysts, no kinetic data are reported. In this contribution, the nopyl acetate production, Scheme 2, using sulfuric acid as a homogeneous catalyst and at different temperatures, feed molar ratios and concentrations of catalyst was analyzed. In this research, the reaction was followed by titration of the acetic acid with standard solution of NaOH at different reaction times, a methodology that has been also reported for following the kinetic of an esterification reaction [28]; also the kinetics of this type of reaction has been determined following the water concentration using Karl Fischer titrator [29]. A kinetic model was proposed based on the acetic acid conversion at different reaction conditions, constant parameters of the kinetic equation were determined and the kinetics was modeled based on concentrations and activities.
2. Experimentation
2.1 Reagents
Toluene (JT Baker, 99.5% w/w), nopol (Boc Sciences, 99.15% w/w), acetic acid (Merck, 99.5% w/w), and sulfuric acid (JT Baker, 97.99% w/w) were used. For the preparation and standardization of the titration solution to quantify the acetic acid, potassium hydrogen phthalate (Merck), sodium hydroxide (Carlo Erba) and deionized water were used; the indicator used for titrations was phenolphthalein in ethanol solution (Chemi, 0.1% w/w).
2.2 Catalytic tests
The esterification reactions were carried out in a 25 mL three neck round-bottom flask heated by an oil bath placed in a hot plate with magnetic stirring and temperature controller (Heidolph MR Hei - Standard, EKT Hei-Con). Stirring was kept constant at 500 rpm to ensure uniform mixing. The reaction was studied at several temperatures (50, 60, 71 and 80°C) with a molar ratio of acetic acid to nopol of 1:1, at several molar ratios of acetic acid to nopol (1:1, 1:2, 1:3 and 1:4) at 80°C with a constant concentration of nopol and catalyst concentrations (0.0184, 0.0275, 0.0367 and 0.0480 mol L-1) with a molar ratio of acetic acid to nopol of 1:1 and at 80°C. A 0.3 M solution of nopol in toluene (20 mL) was added first into the reactor and then heated to the desired temperature, when the temperature was reached, the acetic acid and the sulfuric acid was added. Samples of 0.160 mL were taken at regular time intervals and equal volume of solvent was added for keeping the reaction mixture volume constant; the sample was mixed with 20 mL of distilled water and settled into an ice bath for stopping the reaction and their acetic acid concentration was determined by titration with a standard solution of NaOH 0.1 N and phenolphthalein as an indicator using a Dosimat 775. The acetic acid concentration of each sample was determined with Equation (1) and the acetic acid conversion was obtained with Equation (2). Despite the catalytic activity of acetic acid itself [30,31], the autocatalysis could be ignored under the present experimental conditions because of its negligible contribution to the overall reaction rate. Considering the reaction stoichiometry, the concentrations of the other reactants were calculated from the acetic acid concentration.
Where C i and C f are the initial and final concentration (mol L-1) respectively and A is acetic acid.
As NaOH used in titration procedure could also react with sulfuric acid present in the sample, blank tests were carried out with solvent, nopol and sulfuric acid solution at several temperatures and catalyst concentrations, and the volume found in those titrations was subtracted of the volume of NaOH solution required for the titration of each reaction sample. From repeated experiments, it was found that standard deviation of calculated concentrations was 0.008, 0.013, 0.021 and 0.015 for catalytic tests at 50, 60, 70 and 80°C, respectively.
3. Results and discussion
3.1 Effect of temperature
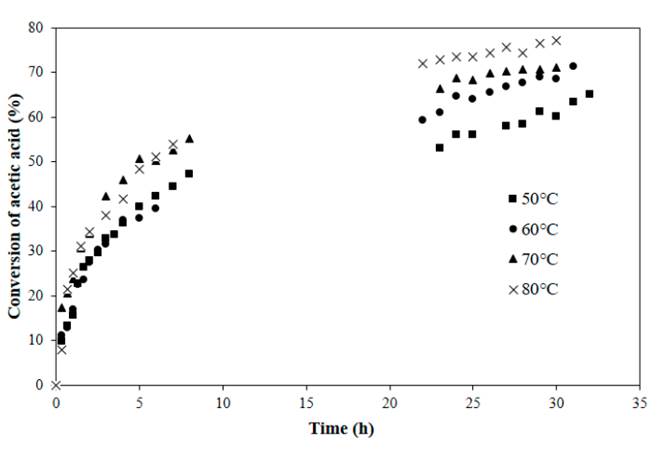
The influence of temperature between 50 and 80°C for a fixed acetic acid to nopol ratio of 1:1 and catalyst concentration of 0.0275 M, was evaluated in the conversion of acetic acid over time, as shown in Figure 1. The conversion of acetic acid increases with temperature because of acceleration of the forward reaction, however the temperature effect is higher after 20 h of reaction. The rate of reaction and hence conversion increases as temperature increased. Equilibrium conversions of 63, 68, 71 and 75% were respectively achieved at 50, 60, 70 and 80°C.
3.2 Effect of catalyst concentration
The effect of the amount of catalyst at 80°C, Figure 2, was evaluated. It was found that at low concentrations of sulfuric acid, acetic acid conversion was lower for short reaction times, but when the reaction reaches the equilibrium the lowest concentrations are favored. It is noteworthy that the reaction performed at 0.0184 M did not reach equilibrium in the studied time. The equilibrium conversion was 76, 75 and 60 % for concentrations of catalyst of 0.0275, 0.0367 and 0.0458 M respectively. The amount of catalyst influences the reaction rate, because more H+-ions become available when the amount of catalyst in the mixture increases. The addition of catalyst caused a change of color of the reaction mixture and the formation of a precipitate when the highest amount of catalyst was used; perhaps this was the cause of its lower activity at high reaction time.
3.3 Effect of initial reactant mole ratio
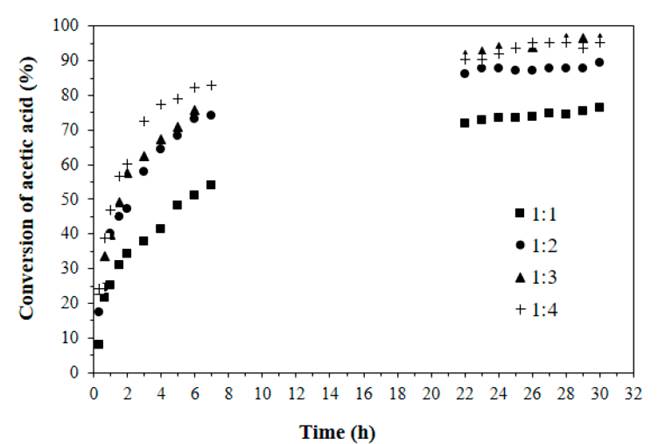
The effect of feed mole ratio at 80°C and with a catalyst concentration of 0.0275 M was studied, as shown in Figure 3. It is remarkable that for an acid: alcohol mole ratio of 1:1 the conversion of acetic acid is much less than for other molar ratios evaluated, this was expected because the reactions with a feed molar ratio of 1: 2, 1: 3 and 1: 4 have an excess of nopol available to react with acetic acid. This trend is similar to those reported for other reactions of esterification with acetic acid [11, 28, 29], and in the esterification of myristic acid with isopropanol and n-propanol using p-toluene sulphonic acid, where the equilibrium conversion decreased when alcohol concentration diminished [30]. It is also noted that for reactions with excess of alcohol, the equilibrium conversion is similar, reaching values greater than 90%. The highest acetic acid conversion (96%) was obtained with a molar feed ratio of acid: alcohol of 1:3 after 28 h of reaction.
3.4. Kinetic model
Concentration based model
Some kinetic models for esterification reactions in presence of homogeneous catalysts have been reported, in the esterification of acetic acid with methanol in the presence of hydrogen iodide [28], sulfuric acid [31] or acetic acid itself [32]; kinetic models were proposed based on concentrations and activity coefficients. Authors found that the fit of the model with the concentration-based description was very good [13]; a reversible second order kinetic rate equation in the case of the use of sulfuric acid as catalyst [28] and the use of activities in the kinetic model instead of mole fractions results in a much smaller residual error [31]. In the esterification of n-butanol with acetic acid catalyzed by noncorrosive Brønsted acidic ionic liquids, it was found that a pseudohomogeneous (PH) kinetic model successfully correlates the experimental data [32]. It was reported that the esterification of myristic acid with isopropanol with n-propanol using p-toluene sulphonic acid as catalyst for a temperature range of 343-403 K, the reactions follow first order kinetics in all components [30]. The majority of the researchers report that an esterification reaction follows second order kinetics, first-order with respect to each reagent [2,14,19,30]. It is assumed an elementary second-order reversible reaction, first-order with respect to each reagent for the reactions carried out with a molar ratio of 1:1 of acetic acid to nopol. The reaction rate expression is presented in Equation (3) [33].
Where C A , C B , C C , C D are the concentrations of acetic acid, nopol, nopyl acetate and water respectively, k f and k b are the forward and backward reaction rate constants, respectively. The reaction rate constants k f and k b are assumed to be linearly dependent on the catalyst concentration. Various studies support this assumption [2,34-36]. As at the beginning of the reaction the acetic acid and nopol concentrations are the same (molar ratio 1:1), there is no presence of nopyl acetate and water and the reaction volume was maintained constant during the reaction, using the definition of conversion, X A , Equation (4) and relating all concentrations in terms of conversion Equation (5) is obtained, where C A0 is the initial concentration of acetic acid.
With the definition of the equilibrium constant, Equation (6) [33], the Equation (7) is obtained.
Since at equilibrium the reaction rate, Equation (7), is zero, the K eq in terms of the equilibrium conversion of acetic acid, XAe, is given by Equation (8) for an equimolar initial concentration.
Equation (9) is obtained by combining Equations (7) and (8).
The solution of Equation (11) can be obtained using Equation (12).
Figure 4 to Figure 7 show linear fits of Equation (13) for reactions performed at 50, 60, 70 and 80°C respectively, with a catalyst concentration of 0.0275 M. In general, a good adjustment of the data was obtained at the tested temperatures, with the lowest value of the correlation coefficient at 70°C.
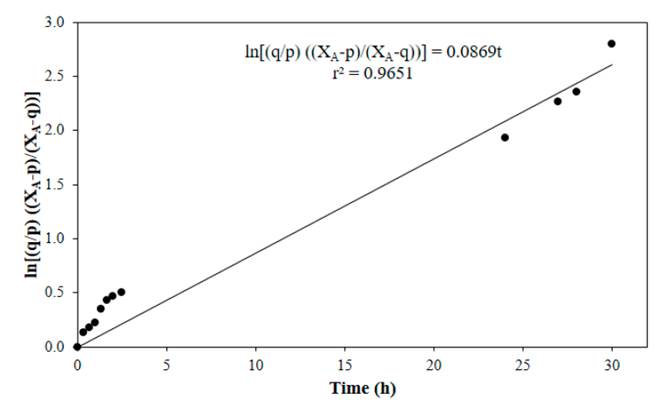
Figure 4 Linear fit of Equation (13) for reaction at 50°C, CH2SO4= 0.0275 M, acetic acid to nopol molar ratio of 1:1, CNopol = 0.2941 M
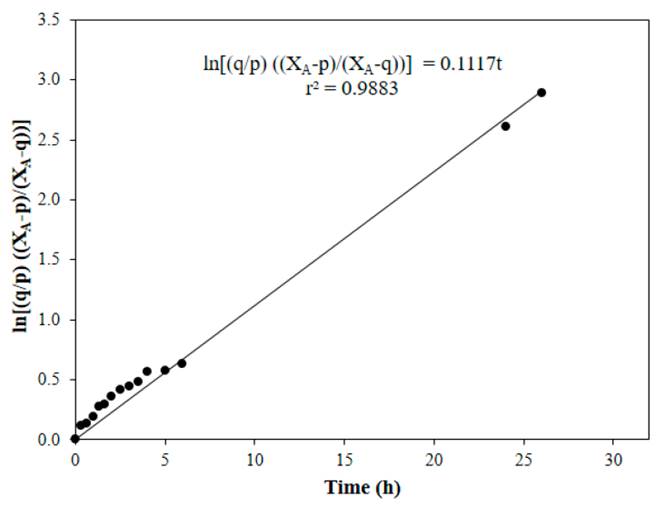
Figure 5 Linear fit of Equation (13) for reaction at 60°C, CH2SO4= 0.0275 M, acetic acid to nopol molar ratio of 1:1, CNopol = 0.2941 M
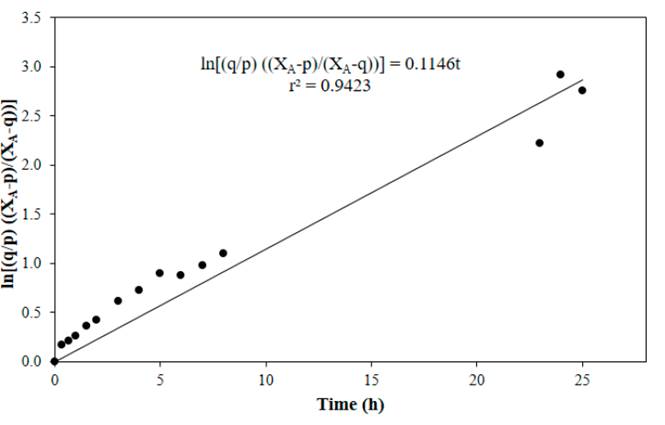
Figure 6 Linear fit of Equation (13) for reaction at 70°C, CH2SO4= 0.0275 M, acetic acid to nopol molar ratio of 1:1, CNopol = 0.2941 M
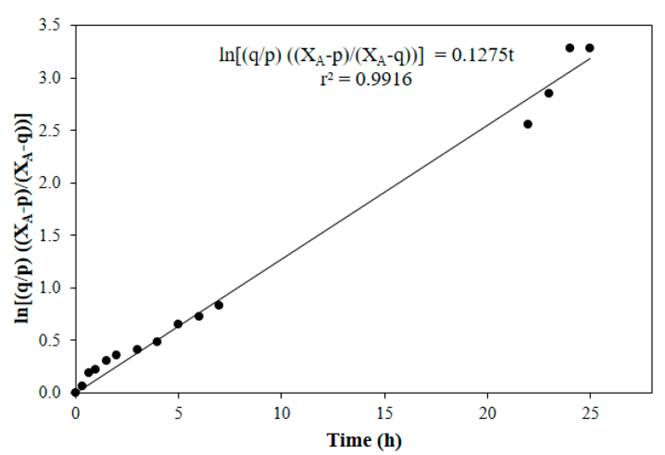
Figure 7 Linear fit of Equation (13) for reaction at 80°C, CH2SO4= 0.0275 M, acetic acid to nopol molar ratio of 1:1, CNopol = 0.2941 M
Table 1 shows the values of the equilibrium constant and the forward and the backward reaction constants at each reaction temperature. Equilibrium constants were determined from Equation (8), the forward reaction rate constants were calculated with the slope of Figure 4 to Figure 7, backward reaction rate constants were determined from the Keq relation, Equation (6). The equilibrium constant values found in this research are in the typical values range (~ 1-10) [13]. For esterification of acetic acid with methanol, an equilibrium constant of 6.2 at 60°C was reported for a methanol to acetic acid molar ratio of 2 [14]. Both equilibrium constants and forward reaction rate constants increase with temperature.
Table 1 Reaction rate constants and equilibrium constants from concentration model for the esterification reaction of nopol with acetic acid
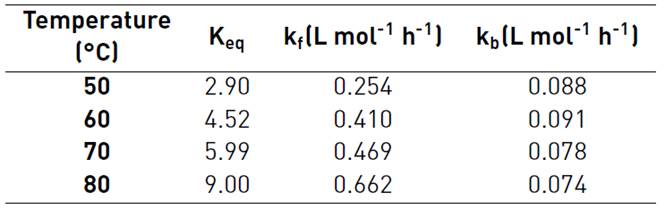
CH2SO4= 0.0275 M, 500 rpm.
The effect of catalyst concentration on the reaction rate is taken in account on the pre-exponential factor (kf0); Figure 8 shows a linear ratio between kf0 and the catalyst concentration at 80°C.
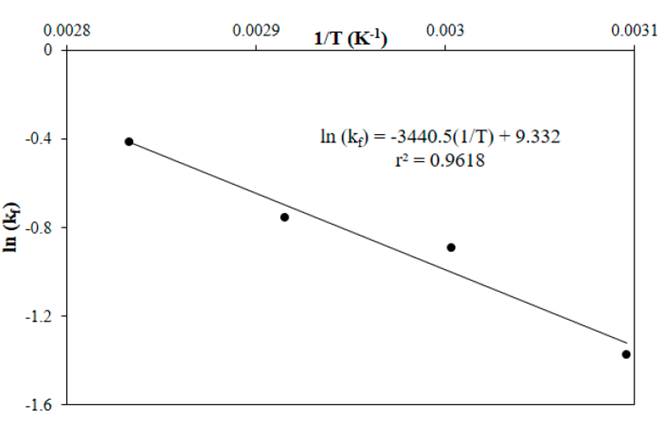
The temperature dependence of the forward reaction rate constant was estimated with the Arrhenius (14), by plotting the logarithm of the forward reaction rate constants shown in Table 1 with respect to the inverse of temperature.
Where k fo is the pre-exponential factor, R is the gas constant, T is the temperature in Kelvin, and E af is the activation energy of the forward reaction.
Figure 9 shows that the Arrhenius plot has a good linear fit, the slope of the straight line corresponds to -Ef/R, so the activation energy of the forward reaction is 28.08 kJ·mol-1. The exponential of the intercept corresponds to k fo and was 11213 L mol-1 h-1. In the esterification of geraniol using a geraniol/acetic anhydride molar ratio of 1:1 and acid ionic liquid, the reported activation energy was 61.8 kJ mol-1 [23]; values of 52.3 kJ mol-1 for acrylic acid with 2-ethylhexan-1-ol [37], 40.7 kJ mol-1 for palmitic acid with isopropanol [38], and 42.07 kJ mol-1 for propionic acid with benzyl alcohol [39] have been reported. The activation energy reported for the esterification of acrylic acid [18] and acetic acid [17] with ethanol in the presence of H2SO4 was 35.04 kJ mol-1 and 65.6 kJ mol-1, respectively.
Activity model
The non-ideality associated with the reaction mixture is evaluated with the activity coefficients, Equation (15), along with the molar concentration or mole fractions [40]. Activity coefficients are calculated using Universal Functional group Contribution (UNIFAC), Universal QUAsi Chemical (UNIQUAC), and non-random two liquid model (NRTL) models.
where, y i , C i , x i and C t represent the activity coefficient, concentration, and mole fraction of each component and total concentration, respectively. The activity coefficients in the reaction mixture were calculated using the UNIFAC method [41]. The compounds used in this study were divided, in a first approach, into structural groups characteristic of the original UNIFAC (CH3, CH2, CH, C, H2O, COO, COOH and OH). Values of known UNIFAC parameters (Rk, Qk and amk), used in the simulations are taken from literature [42] and reported in Table 2 and Table 3.
The chemical activities instead of concentrations can be used in the reaction rate equation:
The equilibrium constant is calculated with Equation (17). The activity coefficients of each compound at the equilibrium molar composition and the K y at each tested temperature are included in Table 4
Table 4 Composition and activity coefficients of components at equilibrium of the reaction at different temperatures

xi is molar fraction
Using Equation (15) into Equation (16), the reaction rate given in terms of activity is obtained, Equation (18):
As the product between the activity coefficients of both reactants and both products does not vary significantly, the rate constants of forward and backward of Equation (18) can be grouped as it is shown in Equation (19). Table 5 shows the values of the equilibrium constant and the forward and the backward reaction constants at each reaction temperature, calculated with the activity model.
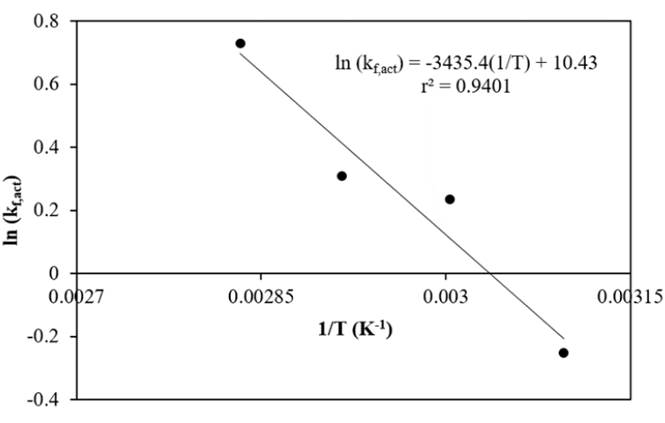
The forward rate parameter k f, act is related to the temperature through an Arrhenius relation, Equation (20)
Table 5 Reaction rate constants and equilibrium constants from activity model for the esterification reaction of nopol with acetic acid
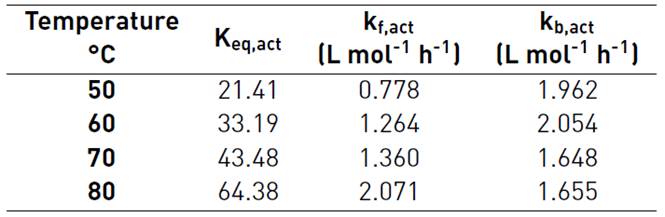
CH2SO4= 0.0275 M, 500 rpm.
The temperature dependence of the forward reaction rate constant obtained from the kinetic model based on activities was estimated with the Arrhenius equation, Equation (20), and the plot is shown in Figure 10. The activation energy of the forward reaction is 28.56 kJ·mol-1 and the k fo,act is 33860 L mol-1 h-1.
3.5 Thermodynamic parameters
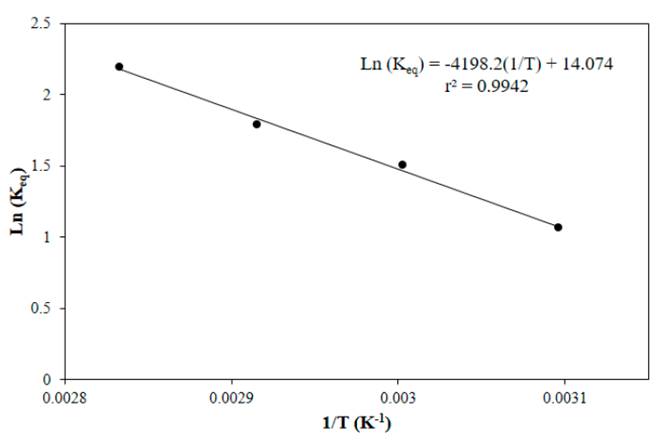
Reaction enthalpy and entropy were determined with the van't Hoff equation [43, 44], Equation (21), by plotting the logarithm of the equilibrium constant, with respect to the inverse of temperature.
Where ΔH° and ΔS° are the enthalpy and entropy of reaction respectively.
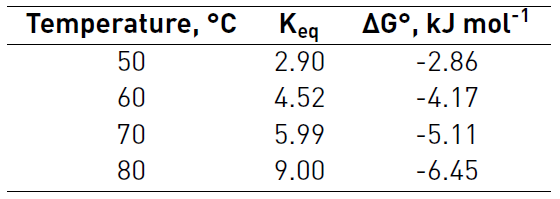
Figure 11 shows the linear fit of the van't Hoff equation in which the slope corresponds to -ΔH°/R, a negative slope means that the reaction is endothermic and a temperature increasing favors the formation of products. The heat of reaction obtained was 34.90 kJ mol-1 and the reaction entropy was 0.12 kJ mol-1 K-1 which means that the system tends to be more disorderly with the course of the reaction. Also for esterification kinetics of acetic acid with methanol (ΔH = 29.99 kJ mol-1) [], esterification of acetic acid with n-amyl alcohol (6.81 kJ mol-1) [], acrylic acid with 2-ethylhexan-1-ol (70.1-74.6 kJ mol-1) [38], acrylic acid with n-butanol (69.03 kJ mol-1) [45], and esterification of acrylic acid with ethanol (71.94 kJ mol-1) [18], endothermic reactions were reported. Because the reaction presents one favorable condition (ΔS > 0) and other unfavorable (ΔH > 0), to determine if it is spontaneous, the calculating of Gibbs free energy Δ°G is required, Equation (22) [46].
The values of Gibbs free energy for all temperatures tested were negative, as shown in Table 6, this means that in the temperature range studied the reaction is spontaneous and the equilibrium constant increases with temperature.
4. Conclusions
The esterification of nopol with acetic acid was carried out in a stirred batch reactor using sulfuric acid as catalyst, the influence of temperature, catalyst concentration and molar feed ratio was studied. The highest conversion of acetic acid was 96% that was obtained at 80°C with a sulfuric acid concentration of 0.0275 M and a molar ratio of acetic acid to nopol 1:3. The activity coefficients obtained with UNIFAC showed that the mixture is nonideal and that the activity coefficients at equilibrium was almost constant in the tested range temperature. For the reactions 1:1 second order kinetic models based on concentrations and activities were developed; the forward and backward reaction rate constants were determined using the linear fit of the model and the equilibrium constant. The forward reaction rate constants and the equilibrium constant showed a tendency to increase with temperature. For the forward reaction, the activation energy estimated was 28.08 kJ mol-1 and the pre-exponential factor was 11213 L mol-1 h-1. Using the kinetic model based on activities gave a forward reaction rate constant of 28.56 kJ·mol-1 and the k fo,act was 33860 L mol-1 h-1. The enthalpy (34.90 kJ mol-1) and the entropy (0.12 kJ mol-1 K-1) of reaction were determined using van’t Hoff equation.