2.1 Case studies

The information used in CEDER was obtained through a Baseline Surface Radiation Network (BSNR) measuring the solar radiation in situ. The period of collection was from May 30, 2012 to March 3, 2015, in total 442,905 five-minute records. For reasons unrelated to the measurement, the information was adjusted according to the corresponding GMT (zero, Soria 2.4° west). On the other hand, the data for the city of Xalapa comes from the meteorological station code No. 76,688 of the National Meteorological Service (SMN), located at 19º30'45.27'', latitude north, 96º54'14.44'' west longitude of the meridian of Greenwich, with an altitude of 1,368 meters above sea level (masl), obtained in the year 2014 every ten minutes.

The granularity of the measurements used in the sites has several applications, namely: knowledge of the operation of the plants, the balancing of the networks, management of units in real time and automatic generation control [¹²-¹⁴]. On the other hand, in smart grids, the main advantage is the regulation of storage to support the electricity market, it also smoothes the photovoltaic output and avoids large voltage and frequency oscillations [¹⁵]. This is the reason why the decision to maintain the periods delivered by the measurement equipment was taken.

The criterion to define the period of analysis was as follows: if it were done on a daily basis, there would be 28, 30 or 31 different characterizations producing an impractical situation, due to the amount of information, and a conclusion of the monthly behavior would not be obtained. If the samples were half-yearly, the seasons of the year would not be considered. If the period of study were every three months, it would involve the seasons; however, they do not necessarily behave similarly. Therefore, it was decided to carry out the study for monthly periods since, around the days 20-23, there is an official change of season, but its characteristics are not yet reflected; that is to say, there are months of transition (March, June, September and December) where the seasonal particularities are not completely fulfilled. On the other hand, this period corresponds, in general, to that of electric billing.

2.2 Monthly reference for solar radiation

The frame of reference closest to the reality of global radiation was chosen among the following tools:

Studies have analyzed the performance of spline functions with typical regression. In [¹⁶], the cubic spline provides a better description between the solar radiation and the hours of sun, also, the errors between the measured and estimated values were more uniform compared to the linear regression. In [¹⁷], the same technique was tested in three cities in Malaysia, reaching the same results from [¹⁶], finding that global radiation decreases faster in relation to the duration of sunlight due mainly to diurnal climate changes.

On the other hand, the autoregressive moving average (ARMA) model is useful to understand and predict the future value of a specific time series,; however, an important requirement for this model is that the time series must be stationary. Nevertheless, the Augmented Dickey-Fuller (ADF) test found that solar radiation is not. In this way, a stabilization stage is necessary to obtain it [¹⁸]. Similar to ARMA, the autoregressive integrated moving average (ARIMA) model focuses its analysis on stationary time series and is based on past values of the variable to be predicted, giving greater importance to the recent past than to the distant past [¹⁹]. One drawback to using ARIMA models is the procedure for order selection, being subjective and difficult to apply [²⁰]. Another drawback of these techniques is the fixed assumption of historical data, it is assumed, implicitly, that past situation will be invariable in the future.

For what has been described above, a conservative criterion was sought, that is, to anticipate what has happened and intuited can occur, in order to locate how radiation behaves in present time. The first two options tend to go to extremes. In this way, the numerical method of spline type adjustment with third-degree smoothing was preferred, which is the most useful when a trend in the function wants to be achieved, reflecting frequently consistent randomness. This type of adjustment is non-parametric in the sense that it does not have coefficients of some polynomial function that fully represents the state of the system. However, it turns out to be highly satisfactory when the response of the system tends to be variant and oscillating in which traditional methods, such as least squares, fail. It is worth mentioning that the ideal behavior would be a Gaussian curve without any environmental oscillation.

2.3 Spline fitting

Parametric models usually adopt patterns of the normal distribution in its variations inherent in the measurement technique, which means that many events may differ numerically with the fitted model. Non-parametric adjustments are all those that do not obtain a functional relation such as Y = f (x₁, x₂,…, x_p). Consequently, they do not necessarily use statistical techniques. In particular, the spline model fits to the behaviour of the (sometimes oscillating) information, with any trend, whose distribution function is not known or the characterization of the curve is not easy to solve in a conventional way, that is to say, it does not assume, a priori, a functional form [²¹]. This setting has the particularity of unite polynomials by segments through nodes, avoiding producing acute changes in the smooth curve of the model allowing the combination of this type of functions.

The spline model plays an important role in the area of engineering essentially due to its favorable properties in oscillating interpolation, its structure of segmented polynomials and their low complexity of implementation [²²]. In this sense, cubic polynomials are the most used because they present an excellent fit to the nodes to admit the change of curvature, optimizing the variation of the adjustment model and its improvement is based on the number of observations considered [²³]. According to [²⁴], the decisive reason for its use is the continuity (calculating a polynomial between each pair of consecutive points), ensuring that the first and second derivative of each polynomial at each node are equal. That is, the splined adjustment does not behave as a single polynomial, achieving a unique smoothed curve. The adjustment type spline with smoothing technique corresponds to the area of numerical methods in conjunction with the calculus of variations. To achieve the characteristics mentioned, the function, the first and the second derivative valued at each x-coordinate, should be the same. If we have the set of points (x _i, y _i), the original observed information with i = 1, 2,…, n., where each x _i can easily be extended to the case of confluent abscissa, meaning that each “x” may contain more than one "y" with some degree of dependency between the adjacent “x´s”, obtaining a cubic polynomial between each pair of consecutive points is defined with a local variable t _i = x - x _i and their corresponding domain h _i = x _i+1 - x _i generating (n - 1) polynomials whose function, first and second derived are shown in Equations (1)-(3):

To solve the function f in (1) and get their four coefficients, conditions of continuity are required in t = 0 and t = h, where the function f must coincide, the first derivative f´and the second derivative f´ at the ends of each polynomial.

The parameter of smoothing lambda (λ) comes from the formulation of the equations of Euler-Lagrange. When λ tends to zero, the resulting curve (presents "greater acuity" vertical) is the classic cubic C-Spline interpolation [²⁵, ²⁶]. When tends to infinity, the resulting curve tends to the line obtained by least squares adjustment. The Euler-Lagrange equations require a joint minimization of the Equation (4):

In the above expression, t _xi is the local variable of each polynomials, g(t _xi) is the joint function of the ( n - 1) polynomials valued in x _i.The lagrangian parameter p must comply with the expression pz = 0 in the obtained minimization. The δy _i are the values that allow creating weightings in the expression calculation process. The auxiliary variable z allows maintaining congruence in the condition pz = 0 that is required comply. The variable S is a function of the smoothing parameter λ so that their behavior is similar. Deeper information about the theoretical spline interpolations family development are in suggested references [²⁷, ²⁸]. The shape and smoothness of a spline relies heavily on this value of smoothing, which is selected from a measure that balances the bias and variance of this class of estimators [²⁹].

2.4 Characterization of the frame of reference

In addition to the considerations listed in section 2.3, the value λ to be used was decided with the criterion of increasing the value of the coefficient of determination (R²) while maintaining a smooth line (low acuity). In the case studies λ, it remained constant at 10,000 for consistency conditions. Each x-coordinate is confluent and middle vertical responses are obtained to pondering the closest observed values with greater weight. The monthly spline settings were accomplished with the JMP statistical application software [³⁰]. When making the decision to characterize the radiation for monthly periods, five and ten minutes, it is required to obtain a curve that represents each month; this can be parameterized with functions, generally, of third degree or higher with a good R² that measures the predictive quality of the model used, its square root represents the correlation coefficient. Thus, 12 characteristic polynomial functions were obtained with high correlations with respect to each setting original spline.

2.5 Intermittence

To use the b-spline function, it was necessary to define the concept of solar intermittency, understood as the decrease in the amount of radiant power, which is function of the geographical position (spatial scale) and the moment in which it is present (scale temporal), received in a place determined by means of a reference pattern.

The difference between the measured radiation and the one found with the splined adjustment indicates the absence or presence of intermittence. If it is negative, it shows its existence in that reading (x) and its magnitude is the amount of power that must supply a back-up system. Individual intermittencies of 5 and 10 minutes or contiguous of longer duration are expected, the adjacent intermittences and their power deficit being accumulated.

3.1 Monthly solar radiation in CEDER

The behavior of the global horizontal radiation in the monthly scenarios in CEDER are presented in Figures 1 and 2, the points measured with the splined adjustment obtained are observed.

Figure 1 Points observed with the monthly spline adjustments in CEDER in the first half of the year 

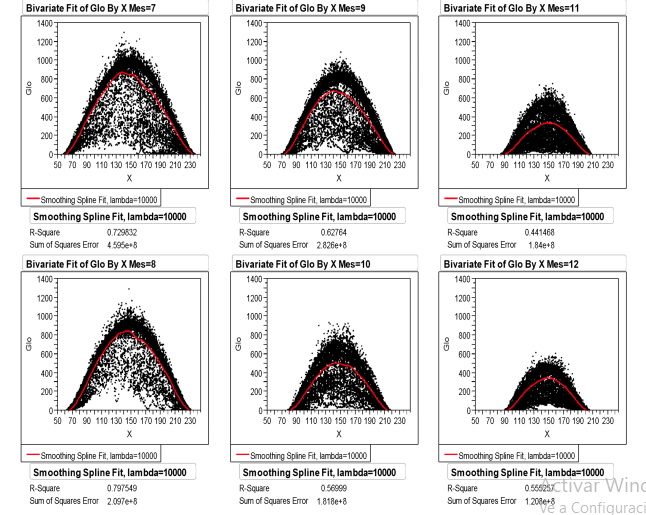
Figure 2 Points observed with the monthly spline adjustments in CEDER in the second half of the year 

It is remarkable the presence of two types of days in each month, except in July and August where this difference disappears. The beginning and end of the radiation vary depending on the month, in this regard, as it is might be expected, it is notable that numbers from reading in the summer months lengthen and shorten in the cold months. The spline radiation peaks reach approximately 800 W/m² in July and August and 350 W/m² in November and January. The correlation coefficients oscillate between 0.664 to 0.893 where the minors correspond to the months of November and March, representing that in spring and autumn there is greater dispersion in information and in summer this is lower.

3.2 Frame of reference characterization in CEDER

Table 1 shows the upward trend of radiation from January to August, due to the climatic stability of the site. In addition, factors such as the amount of information and granularity in the measurement, favor a better approach to reality. According to the scheme presented in the methodology, Table 1 shows the coefficients of the correlations for CEDER. The correlation model is presented in Equation (5):

Table 1 Polynomial coefficients of the spline settings for CEDER 

The Table 1 shows that the best values of R² _spline are presented in the summer months. On the other hand, the polynomials are adjusted with high values of determination, i.e., the worst month (March) has an R² _poly of 0.997 indicating that very high adjustments were achieved. The orders of the monthly polynomials are of 4° and 5°, respectively, the annual analysis presented its best approach with a 6^th order function, where the maximum daily value does not exceed 600 W/m² on average.

3.3 Intermittencies in CEDER

According to the previous relationships, the accounting of the intermittences and their powers are presented in Table 2. The lesser-equal intermittences (I) to 50, 75 and 90% are appreciated as well as the deficits of their powers (P). Table 2 shows that in all the months there were, at 50%, maximum of three intermittencies with a period of 15 minutes, December would need less supply because its deficit is 68.6829 W/m². On the other hand, the maximum duration at 75% of the intermittences was 50 minutes, although the monthly average does not exceed 40 minutes. At 90%, the interval ranges from one hour to two hours with 15 minutes. It is notable that the cold months are the ones that present the highest number of intermittences in the three categories; however, their deficits at 50% are the lowest with an average lower than 100 W/m². Obviously, it is observed that the month with the greatest power insufficiency is April. It is noteworthy that there are 5 months (May-September) with very similar conditions in the number of failures and their power deficits. It can be said that the best month is July, both in the number of intermittencies and in their deficits.

Table 2 Quantification of intermittencies and their power in CEDER 

3.4 Monthly solar radiation in Xalapa

Figures 3 and 4 show the monthly behavior in Xalapa with its respective spline adjustment.

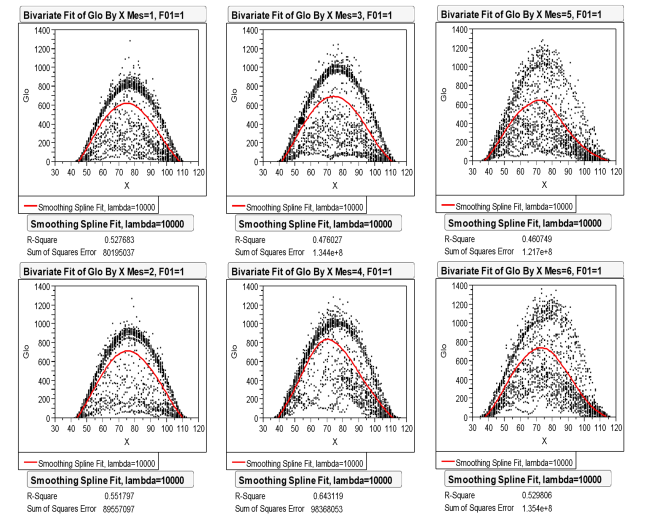
Figure 3 Points observed with the monthly spline adjustments in Xalapa in the first half of the year 

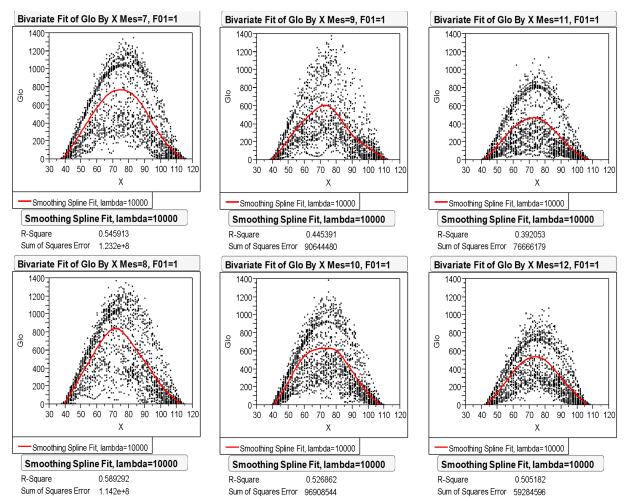
Figure 4 Points observed with the monthly spline adjustments in Xalapa in the second half of the year 

The maximum radiation was reached in the period from 11:40 to 12:50 hrs, with values from 500 to 825 W/m²; the period of sunlight includes from 6:20 to 19:40 hrs. April and August are the months with the highest solar resource and with the best correlation coefficient (r) 0.802 and 0.768, on the contrary, November has an r of 0.626. It is easier to identify the existence of the two types of days than in CEDER.

3.5 A frame of reference characterization in Xalapa

In contrast to the tendency of CEDER, the direction of the radiation is decreasing, reaching its maximum value in April. This behavior is explained by the presence of continuous cloudiness throughout the year, causing greater variability in the radiation. Other causes in the remoteness of high values R² are the number of data and the interval of its acquisition. However, in both places, the month with the lowest solar potential is November, reflecting the worst R². Possibly the biggest difference is found in the annual polynomial adjustment, in the case CEDER a 6th function was necessary and in Xalapa it was 4th.

Table 3 shows the coefficients of the correlations for Xalapa. The table presents the same situation in the orders of the polynomial models even with the smallest number of records, at the same time, the same R² _poly is reached in both cases. The polynomial regressions of the spline adjustments were elaborated at 5% significance (α = 0.05), all β coefficients being significant.

Table 3 Polynomial coefficients of the spline settings for Xalapa 

3.6 Intermittencies in Xalapa

The accounting of the intermittences and their powers are presented in Table 4. The lesser-equal intermittences (I) to 50, 75 and 90% are appreciated as well as the deficits of their powers (P).

Table 4 Quantification of intermittencies and their power in Xalapa 

As shown in Table 4, all months showed a maximum of three intermittencies at 50%, with a maximum period of 30 minutes. On the other hand, the maximum duration at 75% of all the intermittences was 120 minutes, although the monthly average does not exceed 70 minutes. Five hours 10 minutes was the maximum time with 90% of the intermittences. The maximum cumulative intermittencies are presented in November, January and March and the lowest in summer (June-August). As in CEDER, the best month is July, although the lack of power at 50% of the intermittencies is the second most important in magnitude. In the months of seasonal transition, March and the second half of autumn (November and December), the greatest number of intermittences was obtained, as expected in these stations. However, November would need less supply since its power deficit level at 50% is the lowest with 166.043 W/m²; in contrast, March is the month that requires the most support. The most favorable months of the solar resource are from June to August where the number of intermittences is less than 50, 75 and 90% respectively, and, consequently, the power to be back will be close to 34% of the maximum power.

In both cases of study, 50% of the intermittences do not exceed the 3 joint ones, at 75 and 90% the values are similar, although the dispersion is greater in Xalapa. With regard to power deficits, in general, it can be seen that in CEDER less power is lost; however, the average values in the three sections are close. As expected, in Xalapa, due to the measurement, there is a longer duration in the intermittences; however, these amounts are similar to twice the time in CEDER.

The annual analyses were omitted because they do not reflect the monthly or seasonal behaviors, hiding random variations, complicating the calculation of the power to be maintained in each month. On the other hand, [³¹] mentions that most intermittences produce a decrease in the power of 20-30% and that these remain less than a minute, also ensures that if the intermittences are maintained up to six hours cause losses of 80%. In contrast, studies [⁵, ⁶] are not able to predict ten minutes intermittencies, being this period of great interest because of the number of existing events.