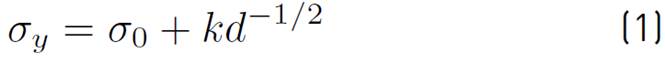English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
The development of materials with higher mechanical resistance, good toughness, and lower specific mass has led researchers to dedicate their efforts to understand the interplay between the mechanical and structural aspects of metals and alloys. Traditional metallic materials are usually polycrystalline with grain sizes in the micrometer scale[1]. These ordinary materials present intrinsic structural defects such as vacancies, dislocations, and grain boundaries (GBs) that strongly affect its mechanical behavior[2].
New materials, such as metallic glasses (MGs), known as amorphous materials, and nanocrystalline (NC) alloys, have been developed in the last decades. In general, these materials exhibit excellent physical and mechanical properties. However, understanding their complex physical metallurgy remains a severe challenge to scientists[3, 4]. Crystalline and MGs materials are quite different concerning the atomic order ranges. MGs present a disordered atomic structure and are thermodynamically metastable solids[5]. Long-range order (LRO) is typical of crystalline materials, whereas it is absent in MGs.
Nonetheless, short-range order (SRO) and even medium-range order (MRO) persist in amorphous alloys[6]. Usually, the SRO corresponds to the local unit involving the nearest neighbor atoms. The MRO encompasses more considerable distances than the short-range of structural configuration; both atomic aggregates influence the MGs' mechanical properties. Moreover, the intrinsic characteristics of crystalline microstructures do not exist in MGs. The classical models currently used to analyze the properties of polycrystals cannot be applied straightforwardly to glassy alloys. NC materials have a mean grain size typically smaller than 100 nm and present higher strength than their coarse-grained counterparts[7, 8]. On the other hand, the mechanical behavior of MGs and NC materials is distinct from the micrometer grain materials, whose crystalline defects are responsible for the elastoplastic properties. Thus, the mechanical behavior dependency as a function of the atomic structure for MGs and NC materials remains not satisfactorily understood[4, 9].
The search for producing bulk MGs and NC samples is a permanent necessity in metallurgy. Indeed, different routes have been developed for MG processing, being the usual ones: the rapid solidification from the liquid state by melt-spinning[10, 11]; the copper mold casting in which the atomic structure of the liquid state is quenched into the solid-state[12]; and the mechanical alloying that produces an amorphous material like powder or small particles followed by consolidation and sintering processes to produce massive samples or additive manufacturing[13]. Nevertheless, the production of NC material directly from the liquid state is a relatively challenging task. In general, three routes are used to produce bulk NC materials: consolidation of mechanical alloying through the sintering of nanopowders[14], severe plastic deformation[14], and crystallization from metallic glass state[15]. This last technique has a broad potential to produce nanocrystalline alloys or at least composite like materials with amorphous matrix and nanocrystals as reinforcement[15]. It is also important to note that the crystallization kinetics behavior is usually determined by isothermal or isochronal treatments[16].
The success of any material in technological applications depends on predicting its mechanical properties via reliable physical models. Hence, the comprehensive understanding of the physical mechanisms responsible for mechanical behavior is a technological necessity. It is well known that the main mechanism of plastic deformation in coarse-grained polycrystalline materials relies on the dynamics of dislocation movements and their interactions[17]. This mechanism prevails for grain size higher than circa dozens of nanometers. However, for smaller grains, it begins to be suppressed[18]. Generally, the usual strategy used to obtain higher strength metallic alloys relies on the model of dislocation pile-up[19], whose strengthening is well described by the Hall-Petch relationship[20, 21], Equation (1).
Where
is the yield stress,
is the frictional stress resisting the motion of gliding dislocations in the absence of grain boundaries, K is the Hall-Petch constant, which is considered to be a measure of the resistance of the grain boundary to slip transfer, and d is the average grain size.
As the grain size decreases, there are fewer dislocations. The stress at the tip of the pile-up decreases so that an increase in the external stress is required to generate dislocations in adjacent grains; thus, the yield strength increases. However, below a grain size of approximately 100 nm, the yield stress may deviate from Equation (1), and there may be even an inverse Hall-Petch relationship when the grain size is smaller than a critical value[18, 19]. The understanding of this phenomenon is not fully clear, but studies indicate that the classical dislocation slip mechanism is not suitable to explain this behavior[9, 20]. Since NC materials possess a significant volume fraction of atoms at or near the GBs, it is expected that a grain-boundary based deformation mechanism to have a critical role in the mechanical behavior[9, 21, 22]. Some mechanisms have been proposed tempting to explain the inverse Hall-Petch relationship, such as the grain boundary sliding (GBS)[23, 24], grain boundary diffusion (GBD)[18, 25], grain rotation (GR)[26, 27], and partial emission dislocation (Shockley dislocation)[9, 28]. Nevertheless, there is hitherto a poor understanding of how these mechanisms actuate.
Among the main topics in the research of MGs, one can cite the glass-forming ability mechanism and mechanical properties, especially the plastic deformation aspects[29-31]. Regarding the latter, it has been proposed that the principal physical mechanism is the formation and rapid movement of the shear bands inside the material volume, which precludes the plasticity yielding[32]. Also, the plastic deformation is strongly correlated with both the SRO and MRO[4].
The complexity of preparing NC and amorphous samples makes the molecular dynamics (MD) an exciting approach to better insight into these materials. For this reason, in this work, we used MD simulations to study the Al80Ti15Ni5 alloy with both amorphous and nanocrystalline structures. This composition was selected due to its capacity to form a ductile amorphous structure similar to the Al87.5Ni10Ti2.5[33]. The MD provides realistic scenarios at the atomic level, simulating diverse structures, and their properties. However, the reliability of the simulated data depends strongly on the interatomic potential. Although there is a Lennard-Jones potential developed for the Ni-Ti-Al alloys[34], the use of another potential is required because of the existing potential, albeit useful for necessary tests on structural properties of the ternary alloy, is not capable of modeling mechanical properties.
2. Simulation method
2.1 Processing of nanocrystalline and amorphous Al80Ti15Ni5 alloy
The MD simulation was performed using the LAMMPS code[35]. Two NC samples containing five and eight grains, both with Al80Ti15Ni5 composition, were generated using the Voronoi tessellation method[36] with an initial size of 15 x 15 x 20 nm3, consisting of 271,829 atoms each. The samples with five and eight grains had an average grain size of 12 and 10 nm, being hereafter referred to as d12 and d10 samples, respectively. The alloy's final stoichiometry was obtained by inserting Ni and Ti atoms randomly into the Al matrix as substitutional solutes. Periodic boundary conditions were applied in all Cartesian directions to remove surface effects. The samples were subjected to energy minimization by the Polak-Ribiere version of the conjugate gradient method and then relaxed at 300 K for 10 ps under the control of Nose-Hoover isobaric-isothermal (NPT) ensemble.
An amorphous sample was created, having as starting material the d10 structure. Initially, the d10 sample was heated from 300 to 2,300 K (above melting temperature) at a heating rate of 10 K.ps-1. Subsequently, the sample was maintained at 2,300 K for 10 ps under the NPT ensemble to stabilize the liquid. Finally, the sample was cooled to 300 K under the cooling rate of 40 K.ps-1 and again stabilized at this temperature for 10 ps. This procedure is similar to that reported in the study of Cu-Zr-Al alloys[37].
The atomic interactions were modeled using the generalized Finnis-Sinclair embedded-atom method (EAM) potential; however, due to the absence of a true ternary potential for the Al-Ti-Ni alloy, we used a ternary potential parameterized by the RAMPAGE method proposed by Ward et al.[38]. The general idea of parametrization methodology and validation is present here.
In the EAM potential, the description of matter is made by the electron wave function, which depends on space coordinates. The wave function's square determines the probability of finding an electron in some located area[39]. Also, the electrons in the multielectron system can be described using electron densities. Each atom's energy in the system is defined as the sum of the energy of the pair interaction of this atom with the other atoms plus the embedded function. In its turns, the embedded function depends on the total electron density of all atoms, except one atom for which the energy is calculated.
To find the atom's total energy, it is necessary to define three functions: the pair interaction energy, electron density, and the embedded function. Quantum mechanical calculations can obtain the functions by fitting some experimental data or determined by using DFT simulations. In the AEM potential, one atom's energy in the atomic structure can be determined by using Equation (2) and (3)[40].
Where U is the total energy of a system of atoms, U
i
is the nominal potential energy of atom i, F is the embedding function,
is the total electron density at atom i that includes electron contributions from other atoms, and
is the pair interaction energy between atoms i and j. According to the EAM formalism, the contribution of electron density at atom i by atom j,
is independent of the environment of atom j.
The EAM/FS or Finnis-Sinclair potentials (FS)[41] have the same basis of the EAM potential, but with a different functional form for the total energy. The RAMPAGE method for build binary or higher-order potentials starts from well-fitted elemental potentials available in the literature. The potentials have been fitted for the one-species systems A and B, and only fit the inter-species cross-potential terms, which is a good compromise between fitting speed and computational accuracy[38, 42]. The functions F
A
, F
B
,
,
,
, and
are thus taken in unchanged form from their original sources, apart from some invariant transformations[38]. The only functions required to be fitted to form a full alloy potential are
,
, and
.
For the pair function, the RAMPAGE method employs a Morse potential formulation. To obtain the inter-species densities
and
, the assumption made is that they are proportional to their respective elemental densities
and
, and the proportionality constants S
a
and S
b
are unknown. Details about the method can be found in[38, 42, 43]. EAM/FS potential for the Al-Ni-Ti system was created from elemental unary potentials reported by Zhou et al.[44]. Each potential used is available at the NIST Interatomic Potentials Repository tabulation[45]. Mixing enthalpy, bulk modulus, and lattice parameter determined by other studies[46, 47] have been used to match the data among DFT, the fitted EAM potentials, and the experimental ones.
2.2 Tensile test and post-processing analysis
The three samples (one MG, two NCs) were submitted to uniaxial tensile tests performed with a strain rate of 1.0 x 1010s-1 at 300 K under periodic boundary conditions. Stresses in the orthogonal directions to the tensile axis, [0 0 1] or z-axis, were zeroed during deformation. The tensile testing was conducted until 0.15 strain. The post-processing analysis was performed using the following tools: Common Neighbor Analysis (CNA)[48], Voronoi analyses[49] and Dislocation Extraction Algorithm (DXA)[50] as implemented in the OVITO package[51], Grain Tracking Analysis (GTA)[52] and LAMMPS X-ray diffraction (XRD) under copper((( radiation
.
3. Results and discussion
3.1 Atomic structure and mechanical properties
Figure 1(a-c) displays the snapshots at 300 K of the samples studied, two NC (named as d12 and d10), and one amorphous. Moreover, the corresponding XRD patterns of the three structures are depicted in Figure 1(d). Diffraction peaks corresponding to Al-a crystalline planes are shown in the diffractograms of d10 and d12 samples, where no clear peaks of secondary phases were observed, indicating that all atoms of Ni and Ti elements are included in the Al-a as solid solution. Also, the peak intensities of the d12 sample are slightly higher than those of d10, reflecting the influence of grain size on XRD intensities. As to the amorphous sample, the massive halo around 40o in Figure 1(d) is typical of a completely glassy structure, in agreement with XRD data reported in[33] for some alloys of the studied ternary system.
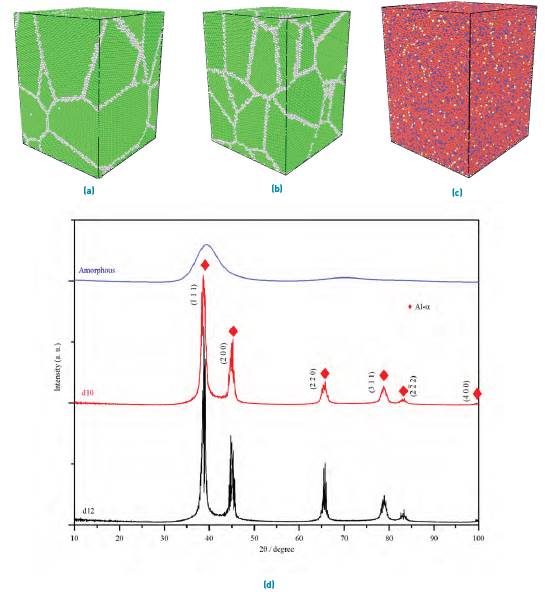
Figure 1 Simulated structures of Al80Ti15Ni5 alloy: (a) d12 and (b) d10. Green atoms refer to FCC structure, and white atoms are those located at grain boundaries. The atomic distribution of amorphous material is depicted in (c). Simulated XRD patterns of NC and amorphous samples are shown in (d)
The simulated uniaxial stress-strain curves are displayed in Figure 2. A higher ultimate tensile stress (UTS) and yield stress are observed for NC structure compared to the amorphous one. The UTS is reached at about 0.07 strain for the amorphous and d10 samples, denoting a tensile strength of approximately 950 MPa and 1,100 MPa, respectively. For the d12 sample, UTS is reached with
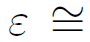0.06 and 1,260 MPa. The UTS values follow an inverse Hall-Petch relationship and are relatively close to experimental values of extruded samples of Al88.5Ni8Ti3.5 alloy with 865 MPa[53].
It is well known that GBs have a strong influence on different material properties. The simplest structural model to analyze an NC material is composed of crystalline grains surrounded by amorphous GBs. The reduction of grain size increases the GB volume fraction that can flow as viscous material under stress, thus reducing the mechanical resistance, in good agreement with our results.
Young’s modulus (E) is obtained from the linear region's slope on the stress-strain curve corresponding to the elastically deformed material. The modulus calculation from the simulation data must include enough data points for a reliable fitting. For this reason, a strain smaller than 0.03 was used to estimate the elastic moduli, resulting in 21.2, 24.7, and 28.8 GPa for the amorphous, d10, and d12 samples, respectively. It is well established for coarse-grained materials that E has low sensitivity to the grain size[54]. However, the obtained results showed a dependency between E and the atomic structure. This type of dependence was also reported in[55] for pure NC aluminum. Considering that GB regions are elastically softer than the crystalline grain interior[56], the reduction of E with the grain size can be explained due to the large volume fraction of GB possessed by the NC materials. Thus, the MGs could be considered a limit-case of NC materials (in which the grain size tends to zero), as already reported for Cu and Cu-Zr based alloy[56, 57]. Nevertheless, the elasticity moduli are lower than the reported for pure NC Al[58]. This quantitative inconsistency can be ascribed to the interatomic potential (see section D).
The stacking fault energy (SFE) determined by Muzyk et al.[59] in pure and alloyed Al demonstrates the significant influence of Ti, decreasing the SFE value from 162 to 93 mJ/m2; however, Ni increases its values to 184 mJ/m2. The addition of both elements improves the partial dislocation emission in the Al-based alloys influencing the deformation modes and decreasing the elastic modulus. Our results show a qualitatively good correlation with the previously cited study.
3.2 Amorphous material and deformation mechanisms
One of the most used methods to analyze the atomic distribution in disordered structures is the pair distribution function that provides a statistical distribution of atoms around a central atom[60]. Although the pair distribution method is an essential analytical tool, it cannot provide accurate information about the three-dimensional atomic configuration. An adequate tool to analyze the SRO in amorphous structures is the Voronoi tessellation technique, where each Voronoi polyhedron (VP) is defined by a set of indices <n3, n4, n5, n6. . .> where ni denotes the number of i-edged bounded faces of the polyhedron around a center atom. In this work, we considered the ten most abundant VP present in the amorphous structure where the <0,2,8,4>, <0,2,8,2>, <0,1,10,4>, <0,1,10,3>, <0,1,10,2> correspond to distorted icosahedral clusters and <0,0,12,0> is the perfect icosahedra. The polyhedrons <0,3,6,4> and <0,3,6,5> are characteristic of FCC-like clusters, and the BCC clusters are represented by <0,3,6,6> and <0,2,8,5>. Figure 3(a) displays the fraction of VP presents at 300 K in the Al80Ti15Ni5 amorphous alloy. Conversely, other types of clusters are eventually present, but they were not considered in our study due to their small population. MRO is roughly based on the VP clusters, such as the Zr-centered <0,2,8,5> polyhedrons, which form an interpenetrating network affecting strongly the mechanical behavior of Cu-Zr based MGs [4]. In this study, the MRO relies mainly on the distorted icosahedral's interconnection, where the <0,2,8,4> VP likely has a greater tendency to form an interpenetrating network.
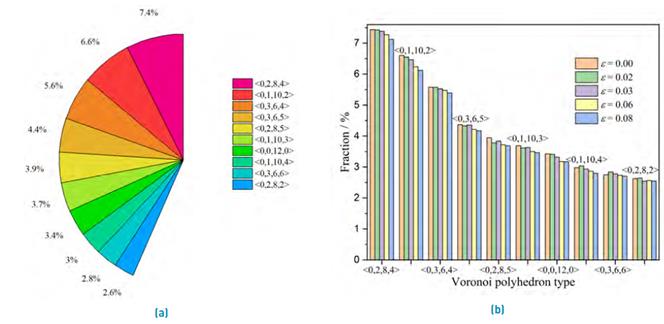
Figure 3 (a) Ten main VP (clusters) present in Al80Ti15Ni5 amorphous alloy at 300 K and without plastic deformation. (b) Evolution of VP with the deformation
It is recognized that the local atomic structures change during tensile deformation, i.e., the strain modifies the SRO and MRO[61]. Thus, the VP evolution as a function of applied strain was analyzed, as shown in Figure 3(b). The polyhedrons <0,0,12,0> and <0,1,10,2> were the ones that suffered the greatest change, being reduced 7.6 % and 7.3 % of its initial configuration, respectively. These changes in atomic configuration caused by shear can be related to the origin of the increased atomic mobility or the starting of shear transformation zones (STZ). Also, the decreasing population in icosahedral clusters during tensile deformation are in good agreement with the reported for Mg-Zn-Ca alloys[62].
Figure 4 presents snapshots of the atomic-level deformation for some strain stages for the Al80Ti15Ni5 amorphous sample. Figure 4(a) displays the sample without strain used as a reference structure. As the stress level increases, the first STZ begin to appear. Also, there are many small regions with a high level of strain distributed homogeneously in the sample's volume, as shown in Figure 4(b). As the deformation continues, the quantity and extension of the STZs are increased, as depicted in Figure 4(c). Most STZs present an inclination about 45 degrees, and some of them coalesce evolving to shear bands [Figure 4(d)).
3.3 Nanocrystalline materials and deformation mechanisms
Due to the small grain sizes, the Al80Ti15Ni5 NC samples behave clearly within the inverse Hall-Petch regime. The atoms are distributed in the interior of grains and the grain boundaries, as shown in Figure 5. The quantity of atoms identified as GB increases with the strain. Conversely, the fraction of atoms in the interior of grains reduces with the strain. This behavior means that mass transport occurs from the grain interior to GB, induced by stress. Concomitantly, the number of defects such as partial dislocations and stacking faults increases, which are in good agreement with decreasing stacking fault energy due to alloying elements. The relative fraction of atoms at the grain interior is higher for the d12 sample than for d10, as expected.
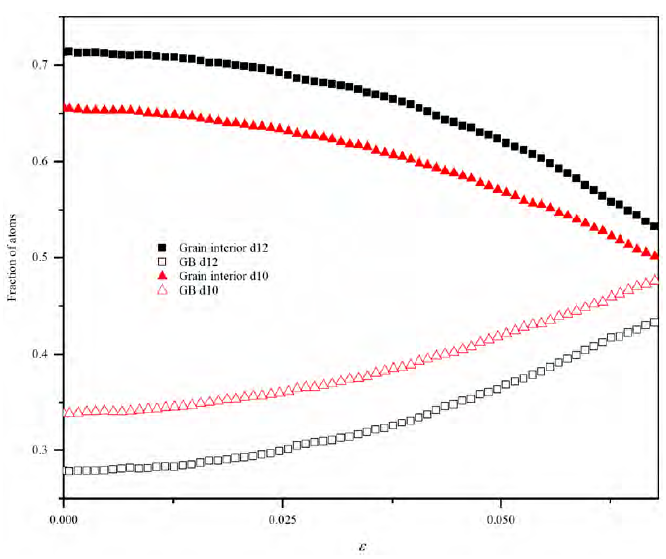
Figure 5 Atomic fraction related to strain for the nanocrystalline samples. GB refers to grain boundary
An essential mechanism of multiplication of dislocations is the Frank-Read source[17]. The stress necessary to activate a Frank-Read source is given by Equation (4)[63].
Where
stands for the shear stress in the plane of dislocation, G the shear modulus, b the magnitude of Burgers vector, and l the distance between two nodes, which can be the grain boundaries.
Considering Equation 4 and the grain features, the maximum possible distance between the pinning points is the grain size. On the other hand, using typical values for G and b of metals, the minimum distance
of an active Frank-Reed source is in the 10-100 nm range[62, 63]. Since the d10 and d12 grain sizes are close to the lower range limit, Frank-Read sources are not expected to be active in the present NC samples, or at least not in a significant way. Hence, only partial dislocations should nucleate, which reduces the material’s strength[9, 18, 64].
To investigate the dislocation dynamics of NC samples, we used the DXA, which has the function of evaluates the dislocation density for different strains. Figure 6(a-d) shows the dislocation segments at 0.00 and 0.06 strain. Frank and Stair-Rod dislocations are present, but their quantities are negligible in comparison with Shockley partials. Perfect dislocations are present just in a small amount at the beginning of deformation and decrease linearly with the strain. However, Shockley partial grow exponentially, as shown in Figure 6(e) for the d12 sample; the parameter
is the dislocation density at a given strain, while
denotes the initial density, and the dislocation ratio is expressed as
. The d10 sample's behavior is similar, except exhibiting a final dislocation ratio of about half compared to d12. Regardless of the sample (d10 or d12), the observed increase of Shockley partials with strain is relatively low. The decreasing of perfect dislocations density is expected since new perfect dislocations are not possible because of the inhibited Frank-Read source described previously. Moreover, the already existent perfect dislocations are dissociated into two Shockley partials or absorbed by the GBs, both processes reducing its density.
Figure 6 Dislocation evolution under different strains. d12 sample: (a) 0.00 and (b) 0.06 strain. d10 sample: (c) 0.00 and (d) 0.06 strain. The colors green, strong blue, light blue, and purple represent Shockley, perfect, Frank, and Stair-Rod dislocations, respectively, while red segments are non-identified dislocations. (e) Normalized dislocation density plotted for d12 sample
As early mentioned, deformation mechanisms usually found in conventional polycrystalline materials at elevated temperatures, such as GBS, GBD, and GR, may be activated at room temperature in nanocrystalline materials[9]. To assess if these phenomena were present in our NC samples, we used the GTA algorithm. Figure 7 shows the results for the GBS and GR analysis for the d12 sample. These values are an average over the five grains. The GTA processing is an intense time-consuming algorithm; hence, the analysis was only performed for the d12 sample and limited to the strain range of 0.040-0.061. These phenomena are expected to be more pronounceable. Surprisingly, the results show almost no rotation of the grains concerning their initial configuration
, at least for the simulated conditions. This result may be caused by the stress fields around the solute atoms. Moreover, GBS seems to have an essential contribution to the overall strain. Considering the grain's 12-nm diameter, the GBS displacement of 0.340 nm yields a GBS strain of 0.028, almost half of the total strain 0.061. It is a worthy note that although the GBS and GBD are two different phenomena, both of them contribute to the global strain, although it is not simple to split their contribution. Moreover, there is an interplay between these processes, i.e., during the deformation of a polycrystalline material, the diffusion affects the sliding and vice-versa[65].
3.4 Influence of interatomic potential
Although a decrease in the elastic modulus is expected within the nanometer regime, the elastic moduli values found in the previous sections can be considered below the expectations. The interatomic potential is crucial in an MD simulation; thus, it is reasonable to consider the potential as responsible for these low values. Since the experimental tensile test with the ternary composition used here is not available in the literature for comparison to the best of our knowledge, we decided to study the elements that compose the alloy separately. For this end, we created aluminum, nickel, and titanium specimens with a mean grain size of approximately 10 nm. These single element samples were simulated using the same criteria as described in section II (ternary interatomic potential) and unary interatomic potentials. The unary potentials used for aluminum, titanium, and nickel are reported in[66-68]. The stress-strain results are displayed in Figure 8, and the elastic moduli in Table 1. The data indicate a deficiency from the ternary potential to reproduce the elastic moduli of pure elements. As expected, the unary potentials are adequate to produce elastic constant for pure elements. Therefore, the E values obtained for the Al80Ti15Ni5 alloy samples were, indeed, affected by the ternary potential. However, it is important to remark that the RAMPAGE method does not aim to find the "best-in-class" potentials but to allow the rapid evolution of the alloy potential[38]. Depending on the system, and the related phenomena, the RAMPAGE method can provide accurate results comparable to the best potentials available or, as in the present work, it can deviate from the experimental results. Nonetheless, MD simulations of alloys that do not have true potentials deserve studies to test the adequacy of potentials sensitive to chemical composition. Moreover, this kind of investigation shed light on the complex phenomena inherent of nanocrystalline and amorphous materials, but its results must be considered qualitatively. It is a worthy note that the EAM potential does not consider the difference in the electrons. Each atom contributes to the different local atomic environments. Several situations depict limitation on the elastic constants' description, especially in systems with a complex phase diagram such as the Al-Ni-Ti system.
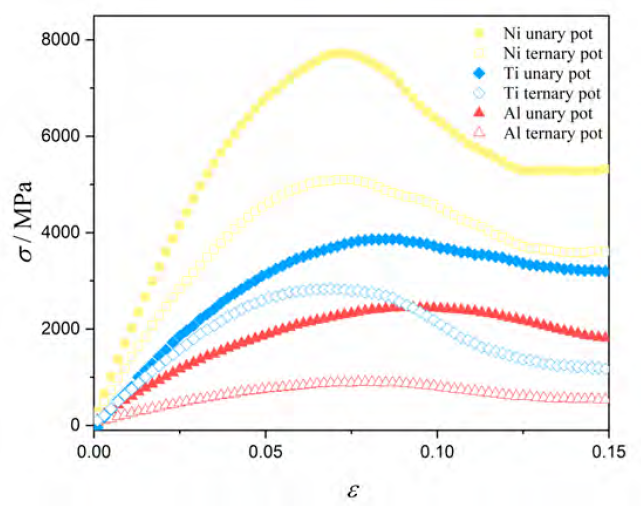
Figure 8 Stress-strain curves for Al, Ni, and Ti with
10 nm using unary and ternary interatomic potentials
4. Conclusions
The mechanical behavior of Al80Ti15Ni5 alloy for amorphous and nanocrystalline structures was studied by molecular dynamics simulation. The Young modulus and the ultimate tensile strength decrease with the nanocrystalline grain size. This fact suggests that the grain boundaries are elastically softer than the interior of nanograins. Furthermore, this behavior indicates that the amorphous structure represents a lower limit-case of the nanocrystalline structure. In the amorphous sample, shear transformation zones were formed still in the elastic regime, and its coalescence becomes shear bands with increasing strain. For the nanocrystalline samples, the data indicate that the plastic deformation of the Al80Ti15Ni5 alloy is governed by the interplay of grain boundary sliding and grain boundary diffusion, which can be interpreted as viscous flow. The reduced grain rotation of less than 0.34o is probably caused by the solute atoms that act as pinpoints. An increase of partial dislocation was observed, but its contribution to the total deformation was limited. For instance, 0.07 strain causes a relatively small increase in dislocation density of just one order of magnitude. Although the ternary interatomic potential used for the Al-Ni-Ti alloy has not shown great accuracy, at least for the elastic moduli, the results can still be useful in a qualitative approach to describe the structural evolution under the strain of the Al80Ti15Ni5 alloy.
