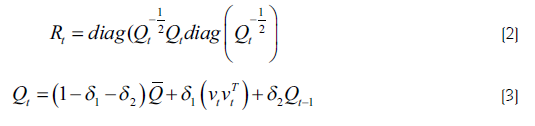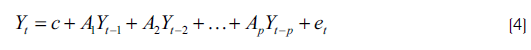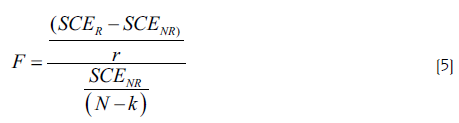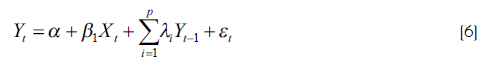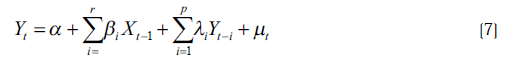INTRODUCCIÓN
La economía peruana, después de 32 años de haber adoptado el modelo de libre mercado, venía mostrando al mundo indicadores macroeconómicos alentadores y con esa carta de presentación venía construyendo relaciones comerciales y financieras con economías desarrolladas y con economías emergentes y países vecinos, suscribiendo acuerdos de tratados de libre comercio y acuerdos bilaterales que permitieron relacionarse comercial y financieramente con el mundo de manera dinámica, actuando en los mercados de bienes y servicios y en los mercados de capitales: tal es así que muchas empresas corporativas peruanas emitieron sus bonos en mercados de Estados Unidos y de Europa: de manera similar lo hizo el gobierno peruano con los bonos, recibiendo una auspiciosa acogida por parte de los inversionistas de los mercados internacionales.
El brote de la COVID-19 fue declarado por la Organización Mundial de la Salud como pandemia mundial, cuando el virus ya había sido reportado en 116 países, incluyendo al Perú, crisis sanitaria que había sacudido los mercados financieros globales. El gobierno peruano había dictado medidas de aislamiento social por 15 días, que posteriormente fueron ampliadas hasta el 30 de junio 2020; desde el 1 de julio 2020, aunque en forma parcial, las actividades económicas ya habían retornado a sus operaciones. Además, según Vega y Sucuple (2020), el Banco Central del Perú (BCRP), para enfrentar la crisis, había tomado medidas monetarias y financieras que propiciaban el funcionamiento de la actividad económica, medidas orientadas a la reducción de costos de financiamiento de mediano y largo plazo y, así mismo, medidas para la mitigación de la variación del tipo de cambio que afecta a los agentes que operan en mercados internacionales y a las familias que tienen pasivos en moneda extranjera.
En otro extremo, es pertinente hacer una breve referencia a la Bolsa de Valores de Lima, que durante la pandemia de la COVID-19 había mostrado evidencias de un fuerte impacto negativo en sus índices más representativos como respuesta a un escenario de incertidumbre, miedo y volatilidad en los mercados financieros globales sobre las expectativas económicas en el corto y largo plazo.
Desde la última semana de enero de 2020, hasta mediados de mayo del mismo año, la bolsa peruana había venido acumulando considerables caídas que llevaron a sus índices más representativos a la pérdida de estabilidad y, en ocasiones, a suspender las negociaciones del día, tras alcanzar el límite de pérdidas. En este contexto económico incierto en el que se observa el incremento de la incertidumbre ante las evidencias de contagio financiero, el Índice General de la Bolsa de Valores de Lima (IGBVL) había mostrado un retroceso marginal de 17,42 %.
Por otro lado, dado que el Perú estaba integrado a mercados de capitales internacionales, le cupo experimentar los impactos negativos de contagio financiero provocado, por ejemplo, por la crisis financiera de 2008, sufriendo cambios en los precios de los activos de renta variable, tal cual puntualiza Rajhans y Jain (2015) sobre los factores que provocan cambios en los precios de los activos financieros de renta variable, siendo uno de ellos el incremento de expectativas inflacionarias.
El estudio empírico de contagio financiero realizado por Akhtaruzzaman et al. (2021) en el contexto de COVID-19, exhibe en sus hallazgos incrementos en las correlaciones dinámicas condicionadas entre los rendimientos de las acciones de empresas localizadas en el mercado de China y las empresas que operan en los mercados de capitales de los países del G-7. Lehnert (2022) estudió la conducta de los inversionistas en el contexto de la COVID-19 identificando sentimientos de miedo como factor importante para tener en cuenta en el análisis de fenómenos de contagio financiero.
Los vínculos entre mercados internacionales son de gran importancia para las decisiones financieras de inversionistas internacionales vinculadas a la estructuración de portafolios de inversión con activos financieros de renta variable, así como para la gestión de las estrategias de salida y entrada hacia otros mercados de renta fija y otros. Los trabajos iniciales de la teoría cuantitativa sobre la conformación de portafolios de inversión desarrollados por Markowitz (1952), la evidencia empírica de Grubel (1968) y el modelo de optimización de portafolio global de Black y Litterman (1992) tuvieron amplia aceptación en las decisiones de la diversificación internacional de portafolios de inversión que conducen a la reducción del riesgo total de una cartera de inversiones y la maximización de los retornos. Por otro lado, el trabajo de modelar la expresión comovimientos de las series de tiempo de los rendimientos de los mercados de valores resulta siendo tarea retadora por tratarse de series de tiempo estacionarias del tipo heterocedástica y condicionada, que en diversas investigaciones se han expresado bajo los modelos del tipo autoregresivo generalizado de heterocedasticidad condicionada (GARCH), estudiado ampliamente por Engle (1982). Así mismo, la aplicación de modelos de vectores autoregresivos (VAR), de análisis de causalidad de Granger (1969), Granger (1988) y Corredor y Vega (2012) en la identificación de respuestas a los impulsos.
Baumöhl et al. (2020) afirman que en las últimas décadas los grandes bancos del mundo se han vuelto más interconectados, y por esta circunstancia, el fracaso de uno de ellos puede desencadenar el fracaso de muchos. Teniendo en cuenta la dinámica de los mercados financieros internacionales, la cercanía y la lejanía de los mercados, se transmiten entre los mercados riesgos financieros. A estos eventos los investigadores han denominado contagio financiero, y al respecto Hansen (2021) afirma que el contagio financiero se define como la propagación de choques entre los actores de los mercados. Por otro lado, Nica (2020) sostiene que en los últimos años las crisis bancarias han provocado una volatilidad significativa del sistema financiero en el mundo. Karungu et al. (2020) afirman que los mercados de valores están muy interrelacionados y los acontecimientos en un lado del mundo están vinculados para afectar los acontecimientos del otro lado del mundo, mostrando evidencias de la transmisión de volatilidad procedente de los mercados financieros maduros hacia los mercados financieros pequeños, como el mercado bursátil peruano.
La importancia y la contribución del presente trabajo se sustenta en el uso de modelos para la generación de indicadores de gestión destinados a los agentes que actúan en los mercados financieros, dado que la transmisión de la volatilidad tiene incidencia en la rentabilidad de los activos de renta variable que cotiza en los mercados bursátiles, en las decisiones vinculadas a la organización de portafolios de inversión, en la fijación de precios de los activos y la política monetaria y, muy especialmente en el Perú, incidencia en la gestión de los patrimonios privados, en los aportantes de Fondos Previsionales y en los pequeños inversionistas de Fondos Mutuos.
En el presente trabajo se utilizaron dos métodos para el análisis del fenómeno de contagio financiero: el método de correlaciones dinámicas, que buscó evidenciar el contagio mediante los coeficientes de correlación dinámica, que se complementó con el análisis hecho con el modelo VAR para la identificación de respuestas a los impulsos, la prueba de causalidad de Granger para identificar acciones de causa-efecto. Por lo tanto, se formularon los objetivos de la investigación en los siguientes términos.
- Analizar las evidencias de contagio financiero que pudieron haber presentado los mercados bursátiles de varios países desarrollados y de algunos países emergentes hacia el mercado bursátil peruano.
- Analizar las evidencias de impulso respuesta que pudo haber dado el mercado bursátil peruano frente a otros mercados bursátiles considerados en el estudio.
- Analizar, en el sentido de Granger, las evidencias de causalidad del mercado bursátil peruano con los otros mercados bursátiles considerados en el estudio.
1. MARCO TEÓRICO
La literatura empírica se ocupó de analizar el tema del contagio financiero utilizando diversos modelos, métodos y técnicas, siendo el más utilizado el enfoque basado en correlaciones, orientado a la identificación de comovimientos en los precios de los activos financieros, en los flujos de capital o en las perturbaciones que ocurren en los mercados de activos reales. Así, el análisis de fenómenos de contagio financiero con modelos para el tratamiento de series de tiempo autoregresivos y de heterocedasticidad condicionada tiene sus inicios en el trabajo realizado por Engle (1982), que introdujo el modelo autoregresivo de heterocedasticidad condicionada (ARCH) al estudio de la variación de la inflación acontecida en Reino Unido, evidenciando el efecto ARCH significativo y el incremento de varianzas estimadas durante la caótica década de 1970. Posteriormente, Bollerslev (1986) propuso una generalización del proceso ARCH sobre la base del trabajo de Engle (1982), dando el nombre de procesos GARCH.
Uno de los primeros estudios en Latinoamérica sobre el contagio financiero fue el de Bernardi (2005), que encontró evidencias de que la turbulencia financiera que se origina en un país se propaga rápidamente a otros países vecinos a través de canales de flujo comercial y financiero. El estudio que aplicó el modelo de correlación dinámica a las series de tiempo del comportamiento histórico del spread de los bonos soberanos de países emergentes latinoamericanos.
En otras geografías, Chiang et al. (2007) estudiaron el modelo de correlación dinámica condicionada (DCC) asimétrico para capturar los efectos del desbordamiento y el grado de interacción en el mercado de capitales de Alemania, en el índice bursátil DAX, verificando incrementos significativos en los coeficientes de correlación dinámica. Dajcman y Festic (2012) estudiaron las dinámicas de comovimiento y desbordamiento de rendimientos bursátiles entre el mercado bursátil de Eslovenia y los mercados de Reino Unido, Alemania y Francia con el modelo DCC MGARCH, evidenciando incrementos significativos en los coeficientes de correlación, demostrando con ello la presencia de contagio financiero. Además, es necesario señalar el análisis empírico realizado por Piffaut y Rey (2016) para detectar el contagio financiero entre los mercados de capitales de Estados Unidos, de Europa y Asia, desde el enfoque del modelo DCC MGARCH.
Las variaciones dinámicas en la volatilidad de los mercados bursátiles tienen influencia en la composición del portafolio de inversiones, tal cual lo demuestra el resultado del estudio de Righi y Ceretta (2012) y de Gorun et al. (2013), quienes hacen notar que, frente a estos eventos de alta volatilidad, las carteras de inversiones tienen que optar por cambios dinámicos. Si dos mercados están moderadamente correlacionados durante periodos estables, la aparición de un choque en un mercado puede llevar a un aumento dramático en el comovimiento del mercado, generando el efecto contagio. Sin embargo, Celik (2012) argumenta que, si la correlación entre dos mercados es tradicionalmente alta, incluso si su correlación estuviera aumentando después de que un mercado experimente una crisis económica, esto no necesariamente genera contagio.
Por otro lado, Trabelsi y Hmida (2018) realizaron el análisis de correlación dinámica condicionada a la rentabilidad diaria de mercados utilizando como muestra a nueve mercados de la zona euro, encontrando incrementados los indicadores de correlación dinámica condicionada, que evidencian la presencia de contagio utilizando el modelo DCC MGARCH. Vera (2019) analiza el problema de contagio financiero en el contexto 20012010 en los mercados de Colombia, México, Perú, Chile y Argentina. Así mismo, Andries y Galasan (2020) se ocuparon de la medición de contagio financiero entre los bancos europeos utilizando el modelo de correlación dinámica, encontrando evidencias resaltantes de la propagación de los efectos del contagio.
El estudio realizado por Gutiérrez (2020) sobre el tema del efecto contagio financiero en los mercados de acciones de América Latina durante la crisis financiera global utilizando el modelo DCC MGARCH de correlaciones condicionales dinámicas multivaria-do, estimó el cambio de correlaciones en el tiempo, mostrando evidencias de contagio financiero del mercado americano hacia los mercados de Brasil, Chile, Perú, Colombia y México, descubriéndose incrementos de correlaciones en el periodo de crisis financiera de 2008.
Corredor y Vega (2020) estudiaron en horizonte de corto plazo el efecto contagio de las variables bursátiles, monetarias y financieras de Estados Unidos sobre el comportamiento de esas variables en el mercado colombiano, analizando la causalidad mediante el test de Granger, la respuesta ante los impulsos mediante el modelo VAR evidenciando incrementos en volatilidad en las variables referidas al mercado de acciones y choques ante el número de noticias. Sandoval-Paucar (2020) estudió bajo el modelo VAR los efectos de propagación de los mercados de Estados Unidos sobre el mercado accionario de Colombia.
Zorgati y Garfatta (2021) estudiaron la proximidad espacial en el problema de contagio financiero durante el periodo de la COVID-19, clasificando la muestra de estudio en dos grupos: el primero, el mercado de China respecto a los países vecinos, y el otro grupo conformado por países que están localizados lejos de China, encontrando manifestaciones de contagio financiero más en países que están lejos de China que en los que están cerca de China. Paskaleva y Stoykova (2021) estudiaron la presencia de contagio financiero entre el mercado bursátil búlgaro y otros mercados, encontrando evidencias que muestran que el mercado de Bulgaria fue expuesto a los efectos de contagio financiero. Wang et al. (2021) estudiaron manifestaciones de contagio en el mercado de Forex, utilizando el modelo DCC MGARCH y buscando identificar canales de transmisión de contagio.
Por otro lado, en la aplicación de modelos DCC MGARCH para el análisis de contagio financiero, tiene especial relevancia el estudio realizado por Gunay et al. (2021) sobre el impacto de la pandemia de COVID-19 en varios sectores del mercado de valores de Australia; en primer lugar, los autores examinaron el contagio financiero entre el mercado de valores de China y los índices sectoriales de Australia desde el modelo DCC MGARCH, encontrando en el tiempo altas correlaciones entre el mercado bursátil de China y la mayoría de los índices sectoriales de Australia. Le y Tran (2021) estudiaron la existencia de contagio financiero entre el mercado bursátil americano y los mercados de valores de Vietnam y de Filipinas mediante el modelo DCC MGARCH, encontrando incrementados en correlaciones dinámicas. Wu et al. (2022) estudiaron el efecto COVID-19 en el problema de contagio financiero a través del modelo DCC MGARCH, y hallaron correlaciones altas de una muestra de 28 mercados bursátiles del mundo.
Corbet et al. (2022) investigaron la presencia de contagio financiero en varios índices bursátiles como expresión del efecto COVID-19, resaltando que todos los mercados, durante el periodo de la crisis, mostraron incrementos en las correlaciones. Sobre el contagio financiero, la literatura registra diversos estudios que utilizaron modelos VAR, como es el caso del análisis de contagio financiero desarrollado por Corredor y Vega (2012), el contagio desde el mercado de Estados Unidos al mercado financiero de Colombia, evidenciando indicios de contagio financiero mediante las pruebas de causalidad de Granger. En otro extremo, Ronderos (2016) estudió el contagio financiero en el periodo de la crisis asiática de 1997 y la crisis mexicana de 1994 utilizando el test de causalidad de Granger.
Por otro lado, Chowdhury et al. (2022) utilizaron el modelo VAR para analizar el impacto de la COVID-19 en la volatilidad del mercado de valores de Estados Unidos, y encontraron evidencias de cointegración y movimientos de forma unidireccional. Shen et al. (2021) utilizaron el modelo VAR para analizar los canales de propagación del riesgo a través de los efectos indirectos dinámicos de la volatilidad dentro de los sectores de la economía de China utilizando datos del mercado de valores. Shobande y Enemona (2021) estudiaron la sostenibilidad de negocios financieros en Nigeria y Ghana utilizando el modelo VAR, evidenciando la importancia de la financiación sostenible en la gestión de los recursos naturales.
Por otro lado, para el análisis empírico de las interrelaciones de las variables se utiliza el modelo VAR. Según Fischer (1977), estos modelos resultan siendo muy convenientes para resumir las regularidades empíricas y sugerir los canales predominantes de transmisión de efectos. Al respecto, Zivot y Wang (2006), afirman que los modelos VAR son flexibles y simples de usar para el análisis de series temporales dinámicas multivariadas y han demostrado ser útiles en la descripción y el pronóstico del comportamiento de series de tiempo económicas y financieras.
Al decir de Londoño (2005), la sola evidencia de correlación entre las variables no constituye necesariamente una relación de causa y sencillamente se acude al análisis de las series de tiempo financieras bajo el planteamiento de Granger (1969), quien analiza la relación de causalidad de forma que afirma que la variable Y es causada por la variable X, o si la variable X coadyuba a explicar el comportamiento de la variable Y, o de forma equivalente, si los coeficientes de la variable X retardada son estadísticamente significativos. El análisis de causalidad se extiende a variables cointegradas cuando la causalidad es una consecuencia necesaria Granger (1988). Además, según Londoño (2005), en el análisis de la dinámica de mercados financieros se busca evidenciar respuestas a los impulsos. En los casos en que se tienen varias series de tiempo, se hace necesaria tomar en cuenta la interdependencia entre ellas.
2. METODOLOGÍA
2.1. Datos
Respecto a los datos requeridos para llevar a cabo el estudio, por conveniencia, siguiendo la estela de relaciones comerciales que mantiene Perú con otras economías, se procedió a seleccionar los índices bursátiles: S&P 500 de Estados Unidos, NIKKEI 225 de Japón, CAC 40 de Francia, IBEX 35 de España, DAX de Alemania, SHANGHAI de China, S&P 500 de México, IPSA de Chile, FTSE de Colombia, BOVESPA de Brasil e IGBVL de Perú. Del mismo modo, se seleccionó el rango de tiempo entre el 3 de enero de 2005 y el 30 de diciembre de 2022. Luego, teniendo en cuenta algunos hechos que han ocurrido en los mercados internacionales que, en cierto modo, han afectado a los mercados de capitales globales, se dividió cada serie de tiempo en cuatro escenarios a efectos de comparar los resultados obtenidos de la correlación dinámica condicionada y, además, del análisis causalidad e impulso respuesta: un primer escenario está comprendido entre 2005-2009, pues en este periodo ocurrió la crisis financiera de los Estados Unidos, precisamente en septiembre de 2008, expandiendo posteriormente la crisis a todo el planeta. Un segundo escenario comprende el periodo 2010-2015, en el que ocurrieron el terremoto de Haití en 2010, el tifón de Filipinas en 2013 y la guerra en Yemen de 2015. Un tercer escenario va desde el año 2016 al 2019, periodo caracterizado por la desaceleración del crecimiento económico. El cuarto escenario es el periodo de la crisis sanitaria de la COVID-19, que se extiende desde enero de 2020 a diciembre de 2022. En la tabla 1 se presenta el listado de mercados bursátiles de los que se ocupa el estudio y de los respectivos índices bursátiles.
Tabla 1 Indices bursátiles de los mercados financieros
| Mercado bursátil | Índice bursátil |
|---|---|
| Estados Unidos | s&p 500 |
| España | ibex 35 |
| Japón | nikkei 225 |
| Francia | cac 40 |
| Alemania | dax |
| China | shanghai |
| México | s&p/bmv inmex |
| Chile | ipsa |
| Colombia | ftse Colombia |
| Brasil | bovespa |
| Perú | s&p Lima General (igbvl) |
Fuente: elaboración propia (2023), con los datos de los índices bursátiles, 2005-2022.
MODELAMIENTO
Una vez concluida la operación de recolección de datos diarios de los índices bursátiles considerados para el estudio, se organizó en una base de datos los índices bursátiles presentados en la tabla 1.
En primer lugar, se obtuvieron la rentabilidad diaria de cada serie de tiempo de índices bursátiles, utilizando la ecuación que se presenta a continuación:
En donde Zt es la rentabilidad diaria expresada en términos porcentuales, P t es el precio en el día t, P t-1 es el precio en el tiempo t - 1.
En segundo lugar, según el objetivo de la investigación, se determinaron los coeficientes de correlación dinámica condicionada para cada escenario, con el propósito de evidenciar las variaciones del fenómeno de contagio financiero ocurrido a lo largo del tiempo y que afectaron al mercado bursátil peruano: para el efecto se utilizó el modelo DCC MGARCH, propuesto por Engle (2002); sus especificaciones se describen en las líneas siguientes:
En donde la matriz de correlaciones Rt no es constante a lo largo del tiempo, 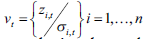 o como un promedio pesado no condicional sobre los residuales estandarizados, y la media no condicional de Qt según Silvennoinen y Teräsvirta (2009) y el diag(Qt) es la matriz diagonal de Qt . La matriz
o como un promedio pesado no condicional sobre los residuales estandarizados, y la media no condicional de Qt según Silvennoinen y Teräsvirta (2009) y el diag(Qt) es la matriz diagonal de Qt . La matriz
Una vez determinada la correlación dinámica condicionada, el paso siguiente analiza el impulso ejercitado desde los mercados bursátiles globales hacia el mercado bursátil peruano, y la respuesta que este había expresado. Se utilizó el modelo VAR, teniendo en cuenta que se tiene un listado de once series de tiempo financieras bajo el supuesto que se afectan entre sí a lo largo del tiempo y, según Novales (2017), no se estima un modelo VAR para realizar inferencias en relación a los coeficientes de variables individuales debido a su baja precisión en su estimación. Su utilidad está centrada en la captura de manifestaciones de impulso respuesta.
Los modelos VAR han sido utilizados para el análisis de las interacciones dinámicas. Es decir, cuando se quiere caracterizar las relaciones simultáneas entre un conjunto de variables, tal cual la expresada en la ecuación que se escribe a continuación:
en donde las variables de la forma Y t que denota a un vector de variables consideradas en el modelo, Y t-1 indica que el valor de la variable i corresponde a periodos precedentes, la variable c es un vector de constantes que sirve como intersección del modelo, A ¡ denota una matriz de parámetros k * k invariante en el tiempo, e t es un vector k que denota el error del modelo. Un modelo VAR es una representación en la forma de ecuaciones simultáneas constituido por un listado de ecuaciones en su forma reducida sin restringir. Las ecuaciones, en su forma reducida, significan que los valores contemporáneos de las variables que conforman el modelo no aparecen como variables explicativas en ninguna de las ecuaciones. Por el contrario, el grupo de variables explicativas de cada ecuación está conformado por un conjunto de retardos de cada una de las variables que conforman el modelo. El modelo VAR presenta en forma alternativa un sistema de ecuaciones simultáneas en el que cada una de las variables están explicadas por sus propios rezagos y los del resto de variables del sistema de ecuaciones.
En el modelo, todas las variables son consideradas endógenas. Los estudios realizados con modelos VAR estuvieron orientados al análisis de las relaciones dinámicas que existen entre las distintas variables, para lo que se han utilizado dos herramientas: la función de respuesta a impulsos y la descomposición de la varianza de los errores de predicción. Al respecto, Sims (1980) y Enders (2014) proponen no diferenciar las series de tiempo, al margen de que presenten raíz unitaria, amparándose en el argumento de que al hacerlo se pierde información importante, relacionada a los comovimientos que se dan entre los datos y a los fenómenos económicos que realmente ocurrieron y que están siendo representados por los datos.
Una vez generado el modelo VAR, se procedió al análisis de las funciones de impulso respuesta de la lista de variables considerada en el estudio, de aquellas que mostraron los efectos de choques en la trayectoria de ajuste de las variables. Una función de impulso-respuesta delinea la respuesta de las variables endógenas ante un choque de una desviación estándar en una de las variables del sistema de ecuaciones. Este choque posee la medida de una desviación estándar, lo que posibilita que se analice como un choque representativo de cualquier otro choque característico en cualquier periodo de la muestra.
Paso seguido, en otro extremo se procedió a realizar el test de causalidad en el sentido de Granger (1969) y Sims (1980), teniendo en cuenta que este tipo de análisis busca identificar si las observaciones pasadas de una variable de series de tiempo posibilitan pronosticar a otra, para decidir la dirección de la causalidad entre dos variables relacionadas y también si se está produciendo retroalimentación o no. Esta indica, de acuerdo con el comportamiento de los datos, si una variable causa a otra. Asimismo, sirve para determinar la presencia del fenómeno de exogeneidad en el modelo, lo que es similarmente igual a decir que no existe. El test permite analizar si X causa a Y o si Y causa a X y dar respuesta a la pregunta de si X causa a Y es para ver cuánto del actual Y puede ser explicado por los valores pasados de Y, y luego para ver si agregando valores residuales de X puede mejorar la explicación de Y.
Para probar si los coeficientes residuales de X son estadísticamente significativos, se utiliza el estadístico F:
En donde:
N: es el número total de observaciones.
K: es el número de parámetros del modelo no restringido.
R: es el número de rezagos.
SCE R : suma de cuadrados del error obtenido con modelo restringido
SCE NR : suma de cuadrados del error del modelo no restringido, se obtiene con la ecuación siguiente:
El procedimiento práctico para la aplicación del test de causalidad de Granger consta de:
En primer lugar, estimar la ecuación (6) aplicando el método de regresión lineal para obtener la suma de cuadrados de error del modelo restringido.
En segundo lugar, estimar la ecuación (7) mediante la aplicación de regresión lineal para calcular la suma de cuadrados de error del modelo no restringido.
En tercer lugar, realizar una prueba de hipótesis con la siguiente expresión:
H 0 : ß 1 = ß 2 = ... = ß r = 0, hipótesis nula que busca demostrar que X no causa a Y.
H 1 =ß j * o, hipótesis alternativa, en este caso la expresión consiste en que X causa a Y.
Para obtener las conclusiones sobre las hipótesis, se utiliza el estadístico de la prueba F y se concluye bajo las condiciones de regla de decisión que se aplica ante la presencia de F calculada.
Y, finalmente, para concluir, se compara el valor de F y calcula con el P-valor calculado para estimar la presencia de causalidad.
3. RESULTADOS
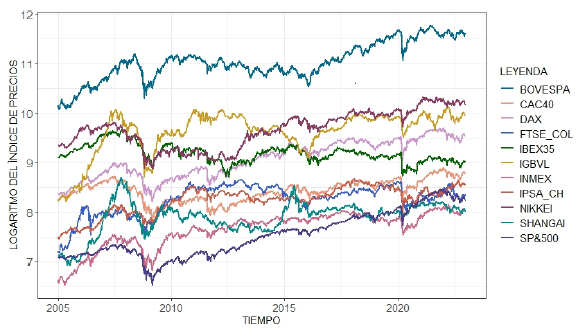
Dentro del conjunto de indicadores e ilustraciones utilizadas en el estudio, para el análisis descriptivo de las series históricas de índices bursátiles considerados para el estudio, la ilustración presentada en la figura 1 es la resultante de haber aplicado la función logaritmo a cada una de las series históricas; esta, de manera clara, permite apreciar las rupturas ocurridas en el periodo de tiempo analizado: se visualiza un primer evento de ruptura de intensidad mayor ocurrido en los últimos meses de 2008 que se extiende hasta 2009, periodo de crisis financiera de los Estados Unidos; un segundo acontecimiento de ruptura de intensidad menor en 2016, y un tercer evento de ruptura de mayor intensidad que se produjo a inicios del año 2020 como efecto de la COVID-19. En estos tres escenarios se aprecian cómo las curvas describen el comportamiento típico de series de tiempo no estacionarias. Según Dajcman y Festic (2012), este tipo de comovimientos en el tiempo entre los mercados bursátiles evidencian indicios de contagio financiero. Se describen movimientos similares entre los mercados bursátiles en los años 2008 al 2009, 2016 y, de manera más pronunciada, en el año 2020.
Fuente: elaboración propia (2023) con los datos obtenidos de índices bursátiles, 2005-2022.
Figura 1 Serie histórica de logaritmo de índices bursátiles 2005: 2022
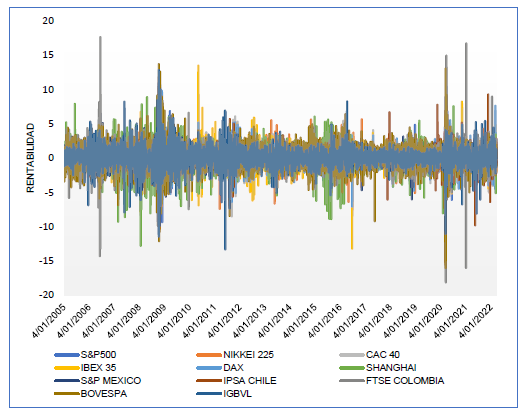
La figura 2 es la resultante de haber aplicado la ecuación (1) a las series de tiempo de índices bursátiles, rentabilidad diaria porcentual de los once mercados bursátiles analizados en el estudio. En la ilustración en referencia se aprecia muy claramente escenarios de alta volatilidad en algunos periodos de las series: así, por ejemplo, el periodo 2008-2020 muestra rasgos de volatilidad muy pronunciada en comparación con otros periodos de tiempo a lo largo de 2005 a 2022.
Fuente: elaboración propia (2023), con los datos obtenidos de índices bursátiles, 2005-2022.
Figura 2 Rentabilidad histórica de los mercados bursátiles
Las cifras mostradas en la tabla 2 refieren los indicadores descriptivos de la rentabilidad diaria de cada uno de los mercados bursátiles. En el indicador de la media de rentabilidad a lo largo del periodo analizado (2005 a 2022), se aprecia que el mercado bursátil peruano exhibe un valor mayor que el de otros mercados, seguido del mercado de Brasil (BOVESPA), del mercado de México (INMEX) y del mercado de Estados Unidos (SYP 500). Los mercados que muestran las más altas volatilidades (desviación estándar) son el mercado de Brasil, China, España y Japón. Estos desbordamientos de variación se propagan rápidamente entre los mercados relacionados que, al decir de Sandoval-Paucar (2020), son indicios de la presencia de contagio financiero.
Tabla 2 Estadística descriptiva de la rentabilidad diaria de los índices bursátiles (2005-2022)
| INDICADOR: | SYP_500 | NIKKEI_225 | CAC_40 | IBEX_35 | DAX | SHANGHAI | INMEX | IPSA | FTSE_COL | BOVESPA | IGBVL |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0,025641 | 0,018058 | 0,011442 | -0,002279 | 0,025986 | 0,020106 | 0,03033 | 0,023738 | 0,02545 | 0,032032 | 0,038241 |
| Median | 0,0688 | 0.0000 | 0,0411 | 0,042 | 0,0745 | 0.0000 | 0,0232 | 0.0000 | 0,0008 | 0.0000 | 0,0222 |
| Maximum | 10,95 | 13,23 | 10,59 | 13,48 | 10,79 | 9,03 | 12,75 | 11,80 | 17,61 | 13,68 | 12,82 |
| Minimum (-) | 12,70 | 12,11 | 13,10 | 15,15 | 13,05 | 12,76 | 7,27 | 15,22 | 18,22 | 15,99 | 13,29 |
| Std. Dev. | 1,24 | 1,43 | 1,37 | 1,45 | 1,36 | 1,53 | 1,25 | 1,14 | 1,14 | 1,71 | 1,43 |
| Skewness | -0,523083 | -0,470515 | -0,262185 | -0,385068 | -0,226323 | -0,61407 | 0,023591 | -0,768804 | -0,672561 | -0,414367 | -0,499934 |
| Kurtosis | 15,71 | 11,42 | 11,13 | 12,79 | 11,10 | 9,18 | 9,84 | 22,44 | 29,56 | 12,21 | 13,72 |
| Jarque-Bera | 30.717,97 | 12.992,88 | 12.523,77 | 18.229,11 | 12.425,98 | 7.490,492 | 8.829,033 | 7.1786,22 | 13,349,20 | 16.103,79 | 21.854,59 |
| Probability | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| Sum | 116,13 | 81,78 | 51,82 | 10,32 | 117,69 | 91,06 | 137,36 | 107,51 | 115,26 | 145,07 | 173,19 |
| Sum. Sq. Dev. | 7.044,058 | 9.372,155 | 8.575,463 | 9.502,965 | 8.341,708 | 10.628,11 | 7.067,984 | 5.873,769 | 8.961,23 | 13.282,96 | 9.320,93 |
| Observations | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 | 4.529 |
Fuente: elaboración propia (2023), con los datos obtenidos de los índices bursátiles, 2005-2022.
Los indicadores de correlación incondicional mostrados en la tabla 3 muestran una relación moderada del mercado bursátil peruano con sus similares de Estados Unidos (S&P 500), Francia (CAC 40), España (IBEX 35) y México (INMEX). Y en el otro extremo, la relación entre leve y baja que existe con sus similares de Japón (NIKKEI 225), China (SHANGHAI) y Chile (IPSA). Todas las relaciones son directas y comparten tendencia estocástica común, y esto significa que todos varían en el mismo sentido, tal cual fue descrito en la figura 2.
Tabla 3 Coeficiente de correlación incondicionada de la rentabilidad diaria de los mercados bursátiles (2005-2022)
| ÍNDICE BURSÁTIL | S&P 500 | nikkei 225 | cac 40 | ibex 35 | dax | shangai | s&p inmex | ipsa Chile | ftse Colombia | bovespa | igbvl peru |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s&p 500 | 1 | 0,1681 | 0,5674 | 0,4803 | 0,5837 | 0,0807 | 0,507 | 0,3379 | 0,3453 | 0,3954 | 0,4142 |
| nikkei 225 | 0,1681 | 1 | 0,3234 | 0,2827 | 0,2928 | 0,3344 | 0,2002 | 0,1237 | 0,1253 | 0,0975 | 0,2127 |
| cac 40 | 0,5674 | 0,3234 | 1 | 0,8572 | 0,9256 | 0,1505 | 0,5074 | 0,3431 | 0,3727 | 0,3046 | 0,4408 |
| ibex 35 | 0,4803 | 0,2827 | 0,8572 | 1 | 0,8087 | 0,1085 | 0,4661 | 0,3263 | 0,3771 | 0,334 | 0,4228 |
| dax | 0,5837 | 0,2928 | 0,9256 | 0,8087 | 1 | 0,1337 | 0,4767 | 0,3557 | 0,3503 | 0,2885 | 0,4343 |
| shangai | 0,0807 | 0,3344 | 0,1505 | 0,1085 | 0,1337 | 1 | 0,1264 | 0,1386 | 0,1163 | 0,0817 | 0,1749 |
| s&p inmex | 0,507 | 0,2002 | 0,5074 | 0,4661 | 0,4767 | 0,1264 | 1 | 0,359 | 0,3915 | 0,4032 | 0,4596 |
| ipsa Chile | 0,3379 | 0,1237 | 0,3431 | 0,3263 | 0,3557 | 0,1386 | 0,359 | 1 | 0,2978 | 0,3333 | 0,3217 |
| ftse Colombia | 0,3453 | 0,1253 | 0,3727 | 0,3771 | 0,3503 | 0,1163 | 0,3915 | 0,2978 | 1 | 0,4161 | 0,3877 |
| bovespa | 0,3954 | 0,0975 | 0,3046 | 0,334 | 0,2885 | 0,0817 | 0,4032 | 0,3333 | 0,4161 | 1 | 0,4006 |
| igbvl | 0,4142 | 0,2127 | 0,4408 | 0,4228 | 0,4343 | 0,1749 | 0,4596 | 0,3217 | 0,3877 | 0,4006 | 1 |
Fuente: elaboración propia (2023), con los datos obtenidos de los índices bursátiles.
La correlación dinámica condicionada, presentada en la tabla 4, se aprecia en el escenario 2020-2022, una relación significativa del mercado bursátil peruano con sus similares de Estados Unidos con 0,40, de México con 0,41, de Brasil con 0,40, de Francia con 0,41, y en el otro extremo, una relación leve o baja con los mercados de China y Japón. Por otro lado, haciendo comparación de los coeficientes de correlación del periodo 2020-2022 con los coeficientes de correlación dinámica de otros escenarios anteriores, resultan siendo significativamente superiores a los coeficientes del periodo prepandemia 2016-2019. Según Trabelsi y Hmida (2018), y Rodríuez y Perrotini (2019), las correlaciones dinámicas incrementadas son evidencia de la presencia de contagio financiero; también, al respecto, Gutiérrez (2020) afirma que son evidencias de contagio financiero ejercitado desde mercados globales maduros hacia mercados pequeños, como el mercado bursátil peruano.
Tabla 4 dcc mgarch por escenarios del mercado bursátil del Perú con otros mercados bursátiles
| dcc mgarch | 2005 - 2009 | 2010- 2015 | 2016-2019 | 2020 - 2022 | % Variación (2020:2022/2005:2009) | % Variación (2020:2022/2010:2015) | %Variación (2020:2022/2016:2022) |
|---|---|---|---|---|---|---|---|
| Corr(s&p, bvl) | 0,3404 | 0,4186 | 0,3683 | 0,3963 | 16,43 % | -5,31 % | 7,60 % |
| Corr(nikkei 225, bvl) | 0,195 | 0,166 | 0,1679 | 0,2113 | 8,36 % | 27,26 % | 25,87 % |
| Corr(cac 40, bvl) | 0,3901 | 0,4005 | 0,3567 | 0,4065 | 4,20 % | 1,50 % | 13,95 % |
| Corr(ibex 35, bvl) | 0,3593 | 0,3504 | 0,3236 | 0,3798 | 5,70 % | 8,39 % | 17,37 % |
| Corr(dax, bvl) | 0,373 | 0,4016 | 0,3407 | 0,3976 | 6,59 % | -0,99 % | 16,69 % |
| Corr(shangai, bvl) | 0,154 | 0,1406 | 0,1438 | 0,1539 | -0,08 % | 9,42 % | 6,99 % |
| Corr(inmex, bvl) | 0,3751 | 0,4036 | 0,3597 | 0,4138 | 10,29 % | 2,52 % | 15,03 % |
| Corr(ipsa, bvl) | 0,3449 | 0,3722 | 0,3453 | 0,3363 | -2,49 % | -9,62 % | -2,59 % |
| Corr(ftse Col., bvl) | 0,289 | 0,2828 | 0,31 | 0,3337 | 15,46 % | 17,99 % | 7,63 % |
| Corr(bovespa, bvl) | 0,3942 | 0,4128 | 0,39 | 0,3991 | 1,23 % | -3,33 % | 2,33 % |
Fuente: elaboración propia (2023), con los datos obtenidos de índices bursátiles.
Si mediante el análisis DCC MGARCH se tienen evidencias de contagio financiero, al decir de Granger (1969) y Sims (1980), es necesario determinar si las observaciones pasadas de una variable de series de tiempo permiten pronosticar a otra, y determinar si una variable causa a otra y, por el otro extremo, es necesario conocer la respuesta ante los impulsos que proceden de otras variables: para identificar este hecho es que se utilizó el modelo VAR. para obtener el modelo para el IGBVL, el que se presenta en líneas siguientes.
IGBVL = 0,204*SYP _ 500(-1) - 0,266*SYP _ 500(-2) + 0,052*NIKKEI _ 225(-1) -0,034*NIKKEI _ 225(-2) + 0,504*CAC _ 40(-1) - 0,350* CAC _ 40(-2) - 0,462*IBEX _ 35(-1) + 0,399*IBEX _ 35(-2) - 0,130*DAX(-1) + 0,106* DAX(-2) - 0,493*SHANGHAI(-1) + 0,536* SHANGHAI (-2) + 1,194*INMEX(-1) - 1,305* INMEX (-2) - 0,146*IPSA(-1) + 0,095* IPSA(-2) + 0,171*FTSE _ Col(-1) - 0,159*FTSE _ Col(-2) - 0,002*BOVESPA(-1) + 0,003* BOVESPA(-2) + 0,964*IGBVL(-1) + 0,026* IGBVL (-2) + 220165
En el modelo arriba expuesto, se observan que, en los coeficientes de las variables influyentes a la Bolsa de Valores de Lima, las influencias más significativas proceden de los mercados de Estados Unidos, Francia, México y China, entre otros, y esto por el flujo comercial y financiero que mantiene el Perú en orden de importancia con China y Estados Unidos. Posteriormente, una vez aplicado el modelamiento VAR, se buscó obtener los efectos de impulso respuesta, cuyos resultados se presentan en la tabla 6 y se ilustran en la figura 3, identificando que la respuesta del mercado bursátil peruano es inmediata y que se manifiesta con rezagos de (1) y (2) ante la innovación que ocurrió en los mercados de Estados Unidos (S&P 500), México (INMEX) y Brasil (BOVESPA), para luego mantenerse el efecto en forma permanente. El número de rezagos 2 es el que optimiza al modelo VAR, tal cual se puede apreciar en el reporte que presenta la tabla 5, y minimiza los indicadores AIC, SC Y HQ; se precisa que el nivel mínimo de AIC se logra en el nivel de rezago 3. Por otro lado, la tabla 5 ilustra también los valores de sentido de Granger a niveles de rezago (1) y (2).
Tabla 5 Test de causalidad de Granger1
| VAR Lag Order Selection Criteria | ||||||
|---|---|---|---|---|---|---|
| Endogenous variables: SYP 500, NIKKEI 225, CAC 40, IBEX 35, DAX, SHANGHAI,INMEX, IPSA, FTSE, COL, BOVESPA, IGBVL | ||||||
| Exogenous | Variables: | C | ||||
| Date: | 1/09/2023 | Time: | 8:27 | |||
| Sample: | 1 | 754 | ||||
| Include | observations: | 746 | ||||
| Lag | LogL | LR | FPE | AIC | SC | HQ |
| 0 | -62209,96 | NA | 7,73E+58 | 166,8122 | 166,8803 | 166,8384 |
| 1 | -48.756,76 | 26.473,58 | 2,32E+43 | 131,0691 | 131,8856* | 131,3838 |
| 2 | --48.502,92 | 492,0246 | 1,62E+43 | 130,7129 | 132,278 | 131,3161* |
| 3 | --48.368,12 | 257,3185 | 1,57e+43* | 130,6759* | 132,9895 | 131,5676 |
| 4 | -48.292,67 | 141,7898 | 1,77E+43 | 130,798 | 133,8601 | 131,9782 |
| 5 | -48.219,32 | 135,6949 | 2,02E+43 | 130,9258 | 134,7363 | 132,3944 |
| 6 | -48.140,3 | 143,8456 | 2,26E+43 | 131,0383 | 135,5974 | 132,7955 |
| 7 | -48.054,1 | 154.3781* | 2,49E+43 | 131,1316 | 136,4392 | 133,1772 |
| 8 | -47.970,6 | 147,0718 | 2,76E+43 | 131,2322 | 137,2882 | 133,5663 |
Fuente: elaboración propia (2023) con los datos obtenidos de los índices bursátiles.
Tabla 6 Impulso de los mercados bursátiles y respuesta de la Bolsa de Valores de Lima (igbvl). Escenario 2020-2022
| Periodo | SYP 500 | NIKKEI 500 | CAC 40 | IBEX 35 | DAX | SHANGHAI | INMEX | IPSA | FTSE _ COL | BOVESPA | IGBVL |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 131,7748 | 33,61617 | 46,3859 | 25,00661 | 6,906051 | 24,11714 | 47,39599 | 25,03916 | 33,58283 | 29,3092 | 232,3635 |
| -9,78979 | -9,14018 | -9,02003 | -8,91709 | -8,89197 | -8,86841 | -8,76175 | -8,65204 | -8,58435 | -8,50706 | -5,99162 | |
| 2 | 142,0104 | 39,21624 | 32,18602 | 0,97554 | -2,501922 | 7,699163 | 75,94496 | 16,79603 | 42,24782 | 25,15918 | 224,0094 |
| -14,2782 | -12,6942 | --13,4932 | -13,662 | -13,5954 | -13,6546 | -13,4885 | -13,33 | -13,2313 | -13,0735 | -11,8991 | |
| 3 | 140,9548 | 44,47071 | 37,53265 | 1,169532 | -4,388337 | 9,866602 | 64,2469 | 13,49771 | 40,05044 | 27,13108 | 223,2201 |
| -15,0828 | -12,5785 | -12,9032 | -13,5613 | -13,7394 | -14,1435 | -13,575 | -14,1217 | -14,153 | -12,404 | -11,9981 | |
| 4 | 140,2679 | 46,29864 | 38,00308 | -2,861108 | -6,06101 | 11,69535 | 61,07624 | 9,77713 | 40,00131 | 26,84607 | 219,8017 |
| -15,3407 | -13,4947 | -13,8635 | -13,7852 | -13,9058 | -15,0676 | -14,3724 | -14,7124 | -14,5808 | -12,9519 | -12,3989 | |
| 5 | 138,1781 | 48,73334 | 38,56945 | -5,750859 | -8,108316 | 13,83964 | 56,55081 | 6,943068 | 39,42155 | 27,22396 | 217,6994 |
| -16,0843 | -14,6683 | -14,99 | -14,2037 | -14,3944 | -16,4527 | -15,4688 | -15,6515 | -15,4177 | -13,5738 | -12,9731 | |
| 6 | 136,6609 | 50,71898 | 39,10077 | -8,703773 | -9,876895 | 15,91252 | 52,51195 | 4,286603 | 38,55778 | 27,39858 | 215,4355 |
| -16,9526 | -15,9493 | -16,3514 | -14,7767 | -15,0464 | -18,0409 | -16,791 | -16,7998 | -16,451 | -14,4609 | -13,7516 | |
| 7 | 135,169 | 52,49492 | 39,40467 | -11,45684 | -11,58339 | 17,92406 | 48,5435 | 1,884375 | 37,57263 | 27,4928 | 213,2855 |
| -17,9096 | -17,2742 | -17,825 | -15,441 | -15,825 | -19,6929 | -18,2063 | -18,0452 | -17,6039 | -15,453 | -14,645 | |
| 8 | 133,7651 | 54,05816 | 39,60479 | -14,06069 | -13,18203 | 19,89213 | 44,71423 | -0,293106 | 36,45757 | 27,49503 | 211,1744 |
| -18,9015 | -18,5856 | -19,3407 | -16,1663 | -16,6848 | -21,319 | -19,6445 | -19,3142 | -18,8089 | -16,5342 | -15,6113 | |
| 9 | 132,4407 | 55,43393 | 39,68308 | -16,52193 | -14,68156 | 21,81234 | 41,02204 | -2,262072 | 35,2385 | 27,41563 | 209,1031 |
| -19,898 | -19,86 | -20,8589 | -16,9265 | -17,5931 | -22,8752 | -21,0648 | -20,5633 | -20,0238 | -17,6619 | -16,6181 | |
| 10 | 131,1792 | 56,6431 | 39,65824 | -18,85297 | -16,08225 | 23,68617 | 37,46584 | -4,039471 | 33,9313 | 27,25718 | 207,0631 |
| -20,8789 | -21,0833 | -22,352 | -17,7046 | -18,5253 | -24,3396 | -22,4434 | -21,7674 | -21,2223 | -18,8136 | -17,6441 | |
| CHOLESKY ORDERING: SYP_500, NIKKEI_500, CAC_40, IBEX_35, DAAX, SHANGHAI, INMEX, IPSA, FTSE_COL, BOVESPA, IGBVL | |||||||||||
| Standard Errors: Analytic | |||||||||||
Fuente: elaboración propia (2023) con los datos obtenidos de los índices bursátiles.
Las cifras mostradas en la tabla 6 se refieren a la función de impulso respuesta, que se observan ilustradas en la figura 3, y que describen la respuesta del mercado bursátil peruano ante el impulso ejercitado por los otros diez mercados de valores considerados en el estudio.
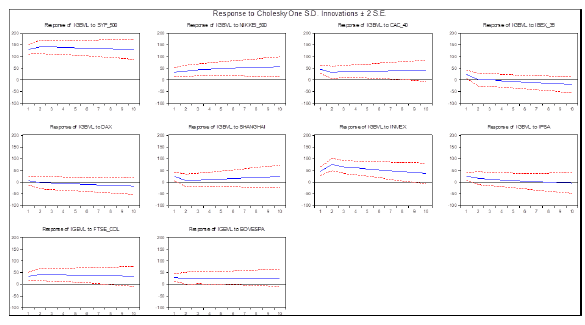
Fuente: elaboración propia (2023), con los datos obtenidos de los índices bursátiles.
Figura 3 Impulso y respuesta de Cholesky
La tabla 6 y la ilustración de la figura 3, son el resultado de haber aplicado el modelo VAR y la opción de impulso respuesta con los datos de los índices bursátiles del periodo de alta volatilidad 2020-2022. Resalta dentro del grupo el efecto shock del mercado bursátil de Estados Unidos al mercado bursátil peruano, que es inmediato con tendencia creciente en los primeros periodos sobre sus propios valores para tener luego un periodo de ajuste rápido con tendencia hacia la baja Sims (1980) expresión de respuesta dinámica a un choque inesperado. También resalta la respuesta del mercado bursátil peruano al accionar del mercado de España (IBEX 35): el efecto es permanente pero lento con una tendencia constante hacia la baja. La respuesta de la Bolsa de Valores, ante la ocurrencia de innovación en el mercado de China (SHANGHAI), es de efecto permanente: al comienzo es bajista para luego estabilizarse en el tiempo. El comportamiento de respuesta bajista por parte del mercado bursátil peruano en el periodo 2020-2022 ha impactado hacia la baja en los precios de activos financieros de renta variable. Como caso particular, se cita el caso específico del Perú, pues en este periodo se ha autorizado el retiro anticipado de fondos previsionales con afectación hacia la baja en la cuota de valor de los fondos.
Tabla 7 Análisis de causalidad de Granger
| Granger Causality Test: | Lags | FStatistic | Probability |
|---|---|---|---|
| (igbvl, syp 500) | 1:9 | 2,7482 | 0,0037 |
| (igbvl, ibex 35) | 1:2 | 6,7535 | 0,0012 |
| (igbvl, inmex) | 1:2 | 4,0888 | 0,0171 |
| (igbvl, ipsa) | 1:6 | 2,5512 | 0,0188 |
| (igbvl, bovespa) | 1:8 | 1,9935 | 0,0447 |
Fuente: elaboración propia (2023), con los datos obtenidos de los índices bursátiles.
Además de los indicadores de correlación, de impulso y respuesta, se requiere identificar y analizar la relación causal desde los otros mercados bursátiles hacia el mercado bursátil peruano, análisis que se ha realizado con la prueba de causalidad de Granger (1969), Granger (1980) y Granger (1988), y como resultante de la aplicación de las ecuaciones (5) y (6) se obtienen los estadísticos F (tabla 7) que, de acuerdo a cada una de ellas, resultan siendo mayor a P _ valor con nivel de significancia estadística de 95 %. Por lo tanto, de acuerdo con lo afirmado por Granger (1988), el efecto a diferentes niveles de rezagos y los movimientos ocurridos en otros mercados han impactado el mercado bursátil peruano. A partir de los resultados presentados en la tabla 7, se concluye que los mercados de Estados Unidos, España, México Chile y Brasil son los que han impactado significativamente en los movimientos del mercado bursátil peruano.
4. DISCUSIÓN
Esta investigación centró su atención en analizar la relación que tuvieron los mercados bursátiles de países desarrollados y de países emergentes con el mercado bursátil peruano en el contexto de la crisis sanitaria de la COVID-19 (2020-2022) y su variación respecto al periodo de prepandemia. Con este propósito se utilizó el modelo DCC MGARCH, a fin de determinar el grado de relación expresado mediante los coeficientes de correlación dinámica condicionada, y para el análisis de impulso respuesta, el modelo VAR y causalidad de Granger. En la investigación se tuvo hallazgos de coeficientes de correlación dinámica condicionada del mercado bursátil peruano con otros mercados notoriamente incrementados en comparación con otros periodos previos a la crisis sanitaria; al decir de Engle (1982), Chiang et al. (2007), Karungu et al. (2020) y Hansen (2021), los coeficientes de correlación incrementados de manera significativa por choques ocurridos en las economías evidencian la presencia de contagio financiero.
Luego, teniendo en cuenta la afirmación de Londoño (2005) y Celik (2012), según la cual una alta correlación entre dos variables no necesariamente confirma la presencia de contagio financiero, se utilizó el modelo VAR para evaluar el impacto dinámico de las perturbaciones aleatorias que ocurren en los mercados financieros y su accionar sobre el sistema variable, pues al decir de Novales (2017), la estimación del modelo no se estima para hacer inferencias acerca de los coeficientes de las variables individuales, pues se estima para identificar el impulso respuesta que existen entre las variables. En ese sentido, las respuestas que ha imprimido el mercado bursátil peruano han sido de reacción inmediata ante los choques procedentes de los mercados bursátiles de Estados Unidos, España (IBEX 35), China (SHANGHAI) y México (INMEX), todas con tendencia a estabilizarse en el tiempo.
Además, se hizo uso de la prueba de causalidad de Granger para localizar si en las relaciones dinámicas del mercado bursátil peruano con los otros mercados bursátiles en estudio, hay mercados que han provocado movimientos estadísticamente significativos en el mercado bursátil peruano. Al respecto, se obtuvieron hallazgos que evidencian impactos procedentes del mercado bursátil de Estados Unidos, de España (IBEX 35), de México (INMEX) y Brasil (BOVESPA) a diferentes niveles de rezagos que van de niveles 1 a 9. Esto, en razón de que el Perú mantiene desde hace un buen tiempo una relación dinámica de flujo comercial y financiero con Estados Unidos y, de manera parecida, con España y México.
CONCLUSIONES
Dado que los problemas de contagio financiero son consecuencia de las crisis desatadas en ciertos países que se transmiten a otros países, las evidencias de contagio financiero expuestas en el presente trabajo, que tiene en cuenta los efectos devastadores que generan, son muy importantes para la política monetaria en el Perú y la fijación de precios en el mercado bursátil, para la organización de portafolios de inversión con activos financieros de renta variable y los inversionistas que actúan en los mercados bursátiles en sus decisiones de entrada, salida y coberturas en la gestión de sus portafolios de inversión, y para los gestores de portafolios de inversión y, en especial en el Perú, para los administradores de fondos colectivos, que constituyen más del 90 % de los actores que se mueven en los mercados de activos financieros.
Para futuras líneas de investigación referidas al estudio de la volatilidad y su transmisión es pertinente abordar la incorporación del componente conductual o emocional en el modelamiento de riesgos financieros.