Introduction
Clinical research should be utilized by physicians as a tool to help reduce uncertainty in scientific knowledge. It seeks to answer questions that can solve problems related to the health conditions of our patients, enabling us to make sound decisions in medical practice1. This process, which refers to the integration of scientific evidence, medical knowledge, and clinical experience, is what defines evidence-based medicine2. Research requires a scientific method, and when it comes to quantitative research, the method involves transforming clinical data into medical knowledge2.
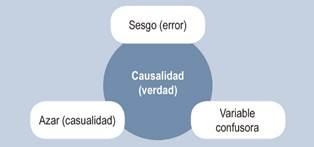
The organization and transformation of this data using mathematical formulas is known as statistical analysis. However, research can yield results that deviate from reality, or in other words, erroneous results (Figure 1). One of the problems that arise in research is the inappropriate use of statistical tests, which stems from a lack of knowledge about statistics and the improper application of research methodology3,4. The risk lies in researchers or readers not recognizing potential errors in research findings and conclusions, known as false positives or false negatives (alpha and beta errors)5. Internal and external validity of research is achieved when the likelihood of alpha or beta error is reduced, and the results are applicable to the target population. A basic recommendation to keep in mind when reading or conducting research is to establish the hypothesis that aims to answer the research question and then determine how to test that hypothesis. In quantitative research, this includes the statistical analysis.
More and more, physicians are now required to justify their medical practices based on scientific evidence, which has led to an increased need for generating clinical research. However, not all physicians are epidemiologists, and many lack a structured understanding of statistics. This classifies physicians into two groups: those who base their medical decisions on guidelines, articles, and protocols, and those with a basic understanding of clinical epidemiology, who can constructively critique the methodology and results of such guidelines, protocols, and scientific articles. Therefore, this review proposes to cover some basic principles that help responsibly critique research studies and provide a foundation for conducting statistical analyses in one’s own research projects.
Basic Concepts: From Simplicity to Understanding the Process of Statistical Analysis
A problem requires a solution, and to address this, a scientific question is posed that seeks to answer the potential solution. The question is formulated based on a proposition derived from prior scientific knowledge and supported by data. This proposition is called a scientific hypothesis and is based on facts and scientific understanding. There is an alternative hypothesis and a null hypothesis, which either confirm or refute the answer to the question. The process of testing the hypothesis is the scientific method in which data are used through observation or experimentation.
Statistical Measures
A statistical measure is a formula or calculation applied to sample data that yields a value, which can then be interpreted to describe the data. There are descriptive statistics related to central tendency (mean, median, mode) and those related to dispersion (standard deviation, range, and variance). Additionally, there are association measures that compare two groups of data between populations. Depending on the research design, these could include relative risk (RR), odds ratio (OR), hazard ratio (HR), among others. It is important to clarify that statistical measures are calculated according to the nature of the variable (e.g., nominal qualitative versus ratio quantitative).
Chance8
Chance refers to an unpredictable outcome due to randomness. In statistics, the result of a statistical measure is neither reproducible nor due to a mathematical algorithm; in other words, the outcome is random and due to chance. The scientific method seeks to minimize random outcomes by establishing probabilities for a phenomenon when crossing variables.
Statistical Significance6
When comparing two groups of data and obtaining a number that indicates their relationship or difference (such as an odds ratio), a mathematical (statistical) formula is applied to evaluate whether the result is due to chance. If it is considered statistically significant, it is assumed there is a low probability that the result occurred by chance (although it can never be guaranteed 100%). The goal is to minimize this chance risk to between 1%, 5%, and 10%, which is why the p-value of <0.05 (less than 5%) is commonly used. Similarly, when comparing results between two groups, statistical formulas are calculated to determine if the obtained statistical measure reflects a real and statistically significant difference. However, it is important to note that this does not always mean that the difference is large, important, or clinically significant.
Bias
When collecting, processing, measuring, and applying mathematical formulas to data, the goal is to show that the values represent the true phenomenon-that is, that they are real. Bias refers to a deviation in the process of collecting, processing, and measuring data, which leads to false results that do not reflect reality. Biases can occur at any stage in the process of database creation and data analysis. Before performing statistical analyses, biases should be measured, quantified, mitigated, and predicted. Recognizing biases is part of the discussion and analysis of results, allowing the reader to evaluate whether they accept the findings and apply them to their clinical practice, considering that the biases do not significantly influence the likelihood of errors in the results. Alternatively, the reader may reject the information due to the risk of obtaining erroneous results in clinical practice. The quality of research is inversely proportional to the level of bias present.
Confounding
When analyzing the association between two variables, A and B, that appears to be reproducible and consistent, but there is a third variable, C, that explains this association, and when controlled-either by removing or matching between groups-the association between A and B disappears. In this case, variable C is a confounding variable.
Causality
Causality is confirmed when one variable is shown to cause an effect in another variable, and this effect is not due to chance, bias, or a confounding variable.
Type I Error (Alpha)
The best way to understand this error is as a false positive. The conclusion indicates that the alternative hypothesis is confirmed and accepted. For example, variable A causes B, or factor C prevents outcome D, among others. However, when the study methodology is replicated, the same result is not obtained, and upon investigation, biases, chance, confounding variables, and other factors are identified. Statistical significance is used to reduce this type of error. It is often compared to “wrongly convicting an innocent person, sentencing them as guilty”.
Type II Error (Beta)
This is a false negative. The conclusion of the study states that the null hypothesis is accepted, meaning there is no causality or association between the variables being tested. However, in reality, this association or difference does exist. It is often likened to “letting a guilty person go free”.
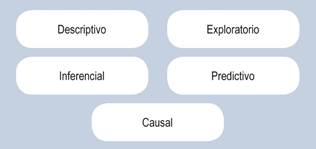
Descriptive Statistics
This type of statistics describes data variables from a population. It covers the entire population and summarizes the data using graphs or statistical measures of central tendency, dispersion (for quantitative variables), or frequencies (for nominal variables).
Inferential Statistics
When it is not possible to describe all the data of a population, random samples (sample sizes) are taken, analyzed, and used to represent (infer) the results for the entire population or to extrapolate to other populations with similar characteristics. To extrapolate study results, statistical formulas are used to estimate the probability that the results represent the population.
Statistical Analysis
Statistical analysis is a mathematical and statistical methodology used to organize, describe, analyze, and interpret data in a valid way, establishing probabilities for extrapolation; in other words, to use the data for decision-making.
Descriptive
The results from a sample database are summarized in tables, graphs, and charts, and can be used to formulate hypotheses. These results cannot be generalized to the entire population; however, they are commonly used in most research designs and form the basis of descriptive observational studies.
Exploratory
This goes beyond descriptive analysis by examining the relationships between variables and seeking associations (correlations) among observations. It aims to control certain variables within subgroups of the database for analysis. Demographic characteristics that differentiate two groups can be identified. Exploratory analysis is used in analytical observational research designs.
Inferential
Descriptive results from a database are subjected to statistical tests that assess whether they can be extrapolated to other similar or general populations. The analysis also evaluates the probability of relationships between variables in the sample and confirms associations and causalities. This type of analysis requires a significant sample size, bias control, and results must be tested to rule out the likelihood of chance. It is used in analytical observational and experimental research designs, as well as systematic reviews.
Predictive
Analytical and inferential results from a research design are applied to mathematical models that estimate future trends, behaviors, or the likelihood of outcomes when variables are modified. It is used in survival designs and economic models.
Causal
This analysis seeks to confirm that a variable not only correlates with another but also causes the effect, without being due to a confounding variable or chance. Different models exist for establishing causality, with the Bradford-Hill model9 being the most recommended. It suggests fulfilling the following criteria: strength of association, consistency, specificity, temporality, biological gradient, biological plausibility, coherence, experimental evidence, analogy, reversibility, and critical judgment. Causal analysis is used in experimental research designs and systematic reviews.
Proposal for Conducting a Statistical Analysis for Quantitative Studies
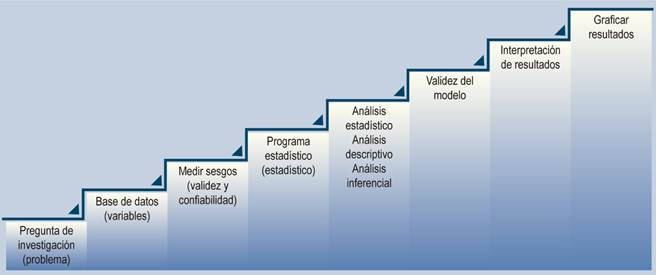
The steps for conducting a statistical analysis in quantitative studies are as follows (Figure 3):
1. Establish the research question and problem: What does the author want to investigate? Propose the null and alternative hypotheses1.
2. Review the database: Explore the data, identify the characteristics of the variables (qualitative or quantitative), and organize the data by variables. Provide a clear and realistic description of the data available. Review the research design4.
3. Evaluate the reliability and validity of data collection: Assess biases in information and measurement. Evaluate how the data were collected and measured, identify potential recording errors, and determine how closely the data reflect what was intended to be measured. Analyze how the data relate to the study subjects10.
4. Select the statistical program: Choose the most practical and reliable statistical software based on the type of analysis needed. Available programs include MS Excel, SPSS, R, Stata, OpenEpi, Epidat, among others.
5. Perform descriptive statistical analysis on each variable, typically represented in the demographic table of an article:
- Frequency distribution (for qualitative variables);
- Measures of central tendency for quantitative variables (mean, mode, and median);
- Measures of variability for quantitative variables (range, standard deviation, and variance).
6. Conduct inferential statistical analysis, taking into account the hypotheses, sample size, and distribution. This analysis is performed when the goal is to present results that readers can use to make decisions in their clinical practice. Design a model that considers and describes the relationship between the data and the study subjects11:
- Parametric analysis: Used when hypotheses involve interval or ratio quantitative variables. Various statistical tests can be applied, such as the Student’s t-test, linear regression, correlation coefficients, difference of proportions tests like the Z standard error, chi-square, Fisher’s exact test, analysis of variance (ANOVA), and analysis of covariance (ANCOVA).
- Non-parametric analysis: Used when hypotheses involve nominal or ordinal qualitative variables. Available statistical tests include Pearson’s chi-square test, binomial test, Fisher’s test, Spearman and Kendall correlation coefficients, tests for cross-tabulations, Wilcoxon, among others12.
- Multivariate analysis: Used when evaluating the effect of more than one variable on an outcome. Available statistical tests include the log-linear model, multiple linear regression, canonical correlation, ANOVA, MANOVA, ANCOVA, and MANCOVA, among others13.
7. Evaluate the model to determine its validity: It is essential to ensure that the database contains all the necessary variables to address the research question, that the method of measuring the variable was the most appropriate, and that the statistical measures or operational metrics selected to calculate differences or associations best describe the phenomenon under investigation. The method can be applied to a different database with similar parameter ranges, and if the results are consistent and reproducible, the model can be considered valid10.
8. Interpret the results using foundational scientific knowledge and propose new hypotheses: It is important to take into account the limitations of the data and the techniques used, as well as any other relevant information that may influence the conclusions2,6,10.
9. Graph and present results: The selection of graphs or result algorithms is not a minor process; the goal is to present the findings clearly and accurately10.
Conclusions
For the results of a study to have internal validity, proper statistical analysis must be conducted. This requires aligning the research question, the study design, and the database that collects the variables to be analyzed. Each variable should be carefully interpreted, and the appropriate statistical methods should be applied for reprocessing and interpretation. It is always crucial to consider how closely the results represent reality, and how much they may be influenced by biases, confounding variables, or chance. A good statistical analysis reduces the probability of error. A medical researcher’s best ally is a biostatistician who can process the mathematical part of the database without losing sight of the clinical concept behind the entire research design.











 text in
text in