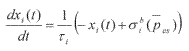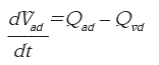INTRODUCCIÓN
El mecanismo de control a corto plazo de la presión arterial (PA) tiene tres componentes principales: los sistemas cardiovascular y nervioso (simpático y parasimpático) y el mecanismo barorreceptor. El sistema de control cardiovascular se encarga principalmente de mantener el flujo sanguíneo hacia el cerebro y el corazón. El sistema nervioso central (SNC) coordina el control reflejo de la PA, y tiene su centro en el bulbo raquídeo. Este mecanismo de control se denomina reflejo barorreceptor. El reflejo se inicia en varios receptores sensitivos periféricos de distensión, denominados presorreceptores o barorreceptores, localizados en las arterias carótidas y aorta (estímulo aferente). Un aumento de la PA distiende los barorreceptores y hace que transmitan señales aumentando su descarga hacia el SNC. Si por el contrario disminuye la presión, se reduce dicha descarga 1.
Estos receptores ubicados en las grandes arterias sistémicas se consideran de alta presión, pues responden a cambios en la PA sistólica y diastólica, en el rango de 60 a 180 mm Hg. Sin embargo, existen otros receptores que actúan de manera similar y están ubicados tanto en la aurícula derecha como en las arterias pulmonares y se denominan receptores de baja presión (RBP). Estos contribuyen al control minimizando los cambios de PA en respuesta a las variaciones en el volumen de sangre; se activan a partir de variaciones, por ejemplo, en el tamaño de las cavidades cardíacas, ocurridas por aumentos o disminuciones del volumen sanguíneo 2. Estas modificaciones de tamaño y volumen dan lugar a alteraciones en la presión intracardíaca que oscilan entre 10 y 25 mm Hg, de ahí su nombre de RBP 3)(4. Su función es contribuir al control de la PA en respuesta a los cambios en el volumen de sangre, es decir, estos receptores ubicados en la aurícula derecha y en las arterias pulmonares no pueden detectar la presión arterial sistémica, pero sí los incrementos simultáneos del volumen sanguíneo en las zonas de baja presión, induciendo reflejos paralelos a los provocados por los barorreceptores ubicados en el seno carotídeo y el arco aórtico; así se logra un control más eficiente de la PA 2.
La Figura 1 resume los diferentes componentes del reflejo barorreceptor como mecanismo de control de la PA; la parte aferente, que envía las señales generadas en los receptores, el sistema eferente que incluye tanto el controlador (SNC) como las señales de respuesta del simpático y el parasimpático y por último los efectores compuestos por el nodo sinusal, el músculo cardíaco y las arteriolas.

Figura 1 Reflejo barorreceptor como mecanismo de control de la presión arterial. Las lineas punteadas denotan el sistema aferente o sensor (señales de trasmision nerviosa al SNC). Las lineas continuas denotan el sistema eferente o controlador (transmision de las senales de control a traves de los sistemas simpatico y parasimpatico) hacia los actuadores (nodo sinusal y arteriolas)
Henson y colaboradores 5 describieron la acción nerviosa sobre los cambios en la PA y la denominaron control por habituación, en el que se ajusta el uso de los sistemas simpático y parasimpático, a fin de obtener una respuesta rápida y estable y a la vez disminuir las acciones a largo plazo 5.
Como alternativa para el estudio de este complejo sistema, la ingeniería biomédica ha utilizado el modelado matemático para el análisis y comprensión de los diferentes procesos implicados en el sistema barorreceptor como mecanismo de control de la PA. Sin embargo, dichos modelos consideran únicamente el comportamiento ampliamente conocido de los barorreceptores del seno carotídeo y del arco aórtico, zonas de alta presión del sistema cardiovascular 6)(14. Tal es el caso de Vallverdú 6 cuyo modelo para el estudio del sistema de control cardiovascular, en pacientes con lesiones coronarias, representa las salidas de los barorreceptores monitorizando la presión sanguínea tanto del seno carotídeo como del arco aórtico, mediante la combinación lineal de la señal de presión, P, y su derivada temporal positiva (dP/dt), ambas filtradas por sistemas de primer orden de constantes de tiempo τ1 y τ2, respectivamente. Esta información se transmite luego a los controladores del sistema cardiovascular. Por su parte Ursino 7, en su modelo del sistema cardiovascular y control nervioso, establece además de la relación dinámica lineal entre la presión en el seno carotídeo y su actividad nerviosa, similar a la representada por Vallverdú, una relación en condiciones estáticas que responde a una forma sigmoidea con un umbral mínimo y una saturación máxima. Otros autores, como Djabella y colaboradores, De Vet y colaboradores, Svetlana y colaboradores 8)(10, también plantean este comportamiento sigmoidal de los receptores y consideran igualmente los receptores carotídeos y aórticos. El modelo planteado por Danielsen 11 y analizado por Ottesen y colaboradores 12 presenta dos alternativas para el modelo del sistema barorreceptor, pero ninguna de ellas considera la contribución de los RBP. Otros modelos más complejos del barorreflejo como el de Doyle y colaboradores 13 utilizan redes neuronales para su simulación. En este caso el diagrama de red neuronal propuesto para el barorreflejo se presenta en lazo cerrado con base en un modelo de dos capas, que reflejan el comportamiento de los receptores de las zonas de alta presión, sin considerar los de baja presión. En resumen, aunque los RBP tienen una participación importante en la variación de la frecuencia cardíaca producto de los cambios en el volumen sanguíneo, los modelos descritos en la literatura solo consideran los receptores de alta presión 6)(14, dejando a un lado la contribución de aquellos ubicados en las zonas de baja presión. En este trabajo se desarrolló una propuesta para el modelado matemático de la actuación de los receptores de las zonas de baja presión, con el fin de contribuir a una representación más realista y completa de la acción de control del sistema nervioso sobre la PA, para un mejor análisis de su comportamiento. El modelo de estos receptores se acopló a un modelo mayor complementando y verificando la acción nerviosa sobre la frecuencia cardíaca como consecuencia de las variaciones de la PA.
MATERIALES Y MÉTODOS
En esta sección se explican las etapas seguidas en el desarrollo del modelo propuesto, haciendo referencia solo a las ecuaciones derivadas para la representación directa de los RBP. Se hizo inicialmente una revisión exhaustiva de la fisiología del sistema cardiovascular y en particular del reflejo barorreceptor. Seguidamente se analizó la contribución al control de la PA de los receptores ubicados en las zonas de baja presión. Posteriormente se plantearon una estructura de funcionamiento y un conjunto de ecuaciones para representar los RBP, ubicados en la aurícula derecha, y se acopló a la estructura básica del modelo del sistema cardiovascular propuesto por Danielsen 11, haciendo algunas modificaciones que se describen oportunamente. Finalmente, se efectuaron las pruebas del modelo acoplado y se obtuvieron los resultados.
La estructura del modelo de Danielsen consiste en un sistema por compartimientos que incluye el corazón, la circulación y el sistema de control. En el corazón se distinguen las partes izquierda y derecha y las circulaciones sistémica y pulmonar. Las partes izquierda y derecha se representan, en el modelo de Danielsen, en función de una elastancia ventricular variable en el tiempo y que representa la función de activación y contractilidad ventricular y una elastancia auricular pasiva. La circulación, tanto sistémica como pulmonar, se divide en cinco secciones, tres para la parte arterial y dos para la sistémica, representadas por ecuaciones diferenciales ordinarias. Tanto el corazón como la circulación son inervados por el sistema nervioso para el control de la PA. Las ecuaciones que describen este sistema se pueden encontrar en el artículo de Danielsen 11. Por otra parte, la respuesta del SNC y/o la parte eferente, en este mismo modelo, se define intuitivamente por el estudio del comportamiento de los datos observados y consta de un componente estático y otro dinámico. El primero equivale a las respuestas de estado estable y el segundo consiste en una ecuación diferencial ordinaria de primer orden que introduce la dinámica temporal, así:
El controlador planteado por Danielsen tiene en cuenta diferente efectores ( xi ), la frecuencia cardíaca, la resistencia periférica en todos los sectores arteriales considerados, el volumen a presión cero y la compliance también en todos los sectores venosos y la elastancia ventricular. El detalle y los valores de los parámetros se pueden encontrar en la referencia 11.
Como parte de los ajustes, a diferencia del modelo base, para el esquema de control se plantea el uso de controladores proporcional-integral-derivativo (PID), para representar el control nervioso de la PA, pues sus características se pueden ajustar al comportamiento fisiológico 15. Este control nervioso tiene efecto sobre la frecuencia cardíaca, la contractilidad y la resistencia periférica 15, pero debido a que los barorreceptores de baja presión influyen sobre la frecuencia cardíaca, solo se detalla en este artículo el modelo de la contribución de dichos receptores sobre la misma. Además, para la circulación sistémica se utiliza el modelo de flujo PoiseuilleHagen 16 y no en función de una resistencia general como en el modelo original, debido a que la acción del sistema nervioso se ejecuta directamente sobre el radio de los vasos sanguíneos considerados.
La disposición de los receptores de baja presión es similar a la de los receptores de alta presión, colocada en paralelo. La Figura 2 muestra el funcionamiento de ambas estructuras como parte del esquema de control planteado. Por medio de líneas punteadas, se diferencian los componentes y el flujo de información de la acción de los receptores de baja presión.

Figura 2 Esquema de control propuesto. La linea punteada representa la contribucion de los receptores de baja presion
El modelo de simulación se ejecuta por cada ciclo cardíaco y para el cálculo de su duración se toma como referencia el modelo de Ursino 7, quien lo calcula como la suma de las acciones simpática y parasimpática. Sin embargo, al igual que Danielsen 11, en su propuesta no considera otros factores importantes que influyen en la frecuencia cardíaca, como los RBP y el automatismo intrínseco del nodo sinoauricular. Se planteó en esta investigación, para aproximar el modelo a un comportamiento más realista, el cálculo del período como la suma del automatismo intrínseco que se produce en el nodo sinoauricular, la contribución simpática y parasimpática generada por la información transmitida por los receptores del seno carotídeo y el arco aórtico, y la estimulación nerviosa provocada por los RBP. El primer factor se adiciona utilizando el modelo IPFM (por la sigla en inglés de Integral Pulse Frequency Modulation) 14)(15, que consiste en una entrada o señal moduladora, m(t), que al actuar a través del modelo IPFM genera los instantes en los que se produciría un latido. Los latidos se generan cuando la integral del ritmo cardíaco instantáneo alcanza un umbral. En ese momento, el proceso se repite. El modelo genera un latido integrando una señal de entrada hasta que alcanza un umbral preestablecido. En ese instante se produce un pulso y el integrador se reinicia 17. El segundo componente es la contribución generada por los sistemas simpático y parasimpático producto de las mediciones y variaciones de la PA y por último la contribución de los receptores ubicados en la aurícula derecha y las arterias pulmonares, generada por los cambios de volumen y cuyo modelo se detalla a continuación.
El algoritmo para el cálculo de la contribución de estos receptores se basa en el concepto de sistemas realimentados. Se considera que la señal generada por los RBP es proporcional al valor máximo del volumen en la aurícula derecha y se compara con el valor promedio referencial en estado normal, originando una señal de error: e2 = Vadmax - Volref . Donde e2 es el error en cada ciclo, Vadmax es el volumen máximo en la aurícula derecha por ciclo y Volref es el volumen referencial promedio, que se establece en 99 mL. ( Vadmax , se calcula a partir de las ecuaciones del modelo base, calculando el valor máximo en cada latido):
donde Vad es el volumen auricular derecho, Qad es el flujo auricular derecho, Qvd es el flujo ventricular derecho (el detalle de las ecuaciones se puede encontrar en la referencia 11).
El valor del error (ec. 2) se envía al sistema de control, que actúa sobre el valor del período de duración de cada ciclo, calculado antes de cada nueva simulación, como se indica en la siguiente ecuación: Tt = T1 + Tp + Ts + re_b . Donde T1 , es el período intrínseco, Tp , la contribución del sistema parasimpático estimulado por los receptores de alta presión, Ts , la contribución del sistema simpático provocado por los receptores de alta presión y re_b, la contribución de los sistemas simpático y parasimpático, producto de la estimulación de los RBP (el modelo propuesto calcula la contribución de la variable re_b; las otras variables forman parte del modelo base al que se acopla).
El modelo calcula el período provocando aumento o disminución de la frecuencia cardíaca en función de la señal enviada por los barorreceptores de alta presión estimulados por los cambios de la presión arterial media (PAM), y la señal enviada por los RBP (re_b) provocados por los cambios de volumen.
Para la contribución de los receptores de volumen se propuso un control proporcional, con la siguiente ecuación: re_b = K e2.
La señal de control es proporcional al error, es decir, su aumento o disminución están basados en las variaciones de volumen desde el valor tomado como referencial o base. El uso de este controlador permite la adecuación de la constante K, para aproximarla al comportamiento fisiológico real. El valor de dicha constante se varió hasta fijarlo en 0,1 para cumplir con el objetivo deseado.
Una vez establecido el modelo para la contribución de los RBP, se acopló al modelo base y se verificó su funcionamiento. Se comprobó en primer lugar que los receptores fuesen capaces de medir los cambios de volumen producidos en la aurícula a partir de los cambios de presión. Esta señal se envió al sistema de control y se graficó como respuesta la contribución de los RBP a la variación de la frecuencia cardíaca, producto de una perturbación. Se graficaron las diferentes situaciones, con y sin la contribución de dichos receptores.
RESULTADOS
Se presentan y discuten algunos de los resultados obtenidos en el modelo de simulación. Según las variaciones de la PA ocurren cambios en el volumen de la aurícula. Si ocurre un aumento de la PA provocado por alguna perturbación externa, se produce un incremento en el volumen. La Figura 3 muestra cómo el volumen se desvía por encima de su valor en estado normal (sin perturbación). El error entre el valor en estado normal y el valor cuando ocurre la perturbación es enviado al sistema nervioso produciendo una alteración en la frecuencia cardíaca, lo cual tiene efecto directo sobre la PA.
La Figura 4 muestra los cambios en la frecuencia cardíaca. Se grafica la respuesta del sistema nervioso sobre dicha frecuencia, teniendo en cuenta tanto los receptores de alta como los de baja presión. Luego se inhibe la acción nerviosa generada por los RBP y se grafica de nuevo. En la gráfica puede observarse la contribución de estos receptores a los cambios en la frecuencia cardíaca.

Figura 4 Respuesta de la frecuencia cardíaca cuando ocurre un aumento de la PAM, sin la actuación de los RBP (línea gruesa) y con ella (línea delgada)
Por efecto de los RBP se obtiene una frecuencia cardíaca promedio de aproximadamente 49 latidos por minuto, mientras que el promedio de la frecuencia sin la contribución de dichos receptores es de 54 latidos por minuto. Se verifica la contribución sobre la frecuencia de las señales enviadas por estos receptores cuando existe una perturbación y se mejora la acción sobre la PA con una disminución adicional de la frecuencia.
DISCUSIÓN
Los resultados obtenidos incluyendo los RBP, como parte del mecanismo de control de la PA, permitieron, en primer lugar, obtener un modelo fisiológicamente más realista al considerar factores que no se habían tenido en cuenta en modelos anteriores, lo que permite una mejor comprensión de la acción nerviosa para el control de la PA. En segundo lugar, el comportamiento del modelo desarrollado se ajustó a los requerimientos planteados para estudiar con un modelo sencillo la contribución de estos receptores al control de la PA. Por último, el modelado matemático, en general, permite el análisis de los sistemas reales a partir de la simulación de diferentes estados o situaciones del sistema. Qué tan eficaz sea el estudio dependerá en primer lugar de su objetivo y, según este, de los factores que se tengan en cuenta para su diseño. Un buen modelo deberá estar ajustado, en la medida de lo posible, a la realidad de su comportamiento, para que pueda ser de utilidad en el estudio del sistema que está siendo representado.
AGRADECIMIENTOS
El trabajo de uno de los autores 2 fue parcialmente apoyado por el proyecto Prometeo de la Secretaría de Educación Superior, Ciencia, Tecnología e Innovación de la República del Ecuador.