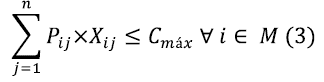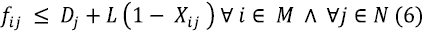I. Introduction
Scheduling of activities in manufacturing and service enterprises should perform efficiently, due to its impact on productivity and competitiveness. Scheduling should contribute to have a greater control of the productive system operations to achieve the proposed goals, and thus to gain a competitive advantage in the market 1-6. Regarding scheduling, difficulties arise from the lack of balance between the production capacity and the capacity of meeting the client's demands in an opportune way 2,7-11.
Production planning is an optimization problem 5. The literature presents cases of activity programming in areas like textile, transport, office, aluminum metallurgy, semiconductor production, molding plastics, and printed circuit boards, among others 12. Further, optimization contributes to the allocation, transport, cutting of materials, plant distribution, forecasts, classification of inventories, production planning, and production scheduling 2,3,13. For sequencing and programming tasks in automated cells, scheduling of storage with muffling in intermediate stages, operations sequence in an assembly system, or for scheduling of tasks in parallel machines with deadlines, it is necessary to minimize the total processing time (makespan), the total time of the system tasks flow, the satisfactory delivery times, the efficient use of resources, the idle time of servers or machines, and the completeness of orders, among others 14.
In industrial production processes, it is possible to work in one or more of the productive stages with parallel machines, which contributes to improve the work execution and to distribute a job between several resources or type of products. All problems of allocation and sequencing in parallel machines, which seek a proximate way to assign and perform jobs on different machines, belong to the NP-Hard class and are fundamental in manufacturing industries 1,4,9,12-13,15-19.
The literature depicts heuristics solutions, metaheuristics, and exact methods that consider Branch and Bound, Branch Price algorithms, Columns Generation, Benders and Danzig Wolf decomposition, linear and lagrangian relaxation, Giffler and Thompson (for active problems and without machines delay), Johnson (for flow shop problems of 2 and 3 machines), Johnson (for job shop problems of 2 machines and multiple jobs), Page's method, CDS algorithm, NEH algorithm , Gupta method, and IG algorithm 2,8.
Our case study considered ten drying chambers (machines) in parallel, of three different technologies, with different temperatures, capabilities and times. More than 40 different products that entered the dryers as requirements were differentiated for avoiding the mix up of density and type of fiber (central or lateral).
In this study, a mathematical model, based on linear programming, is proposed using AMPL software. In addition, a statistical analysis is conducted to evaluate the quality of the solutions provided by the CPLEX and GUROBI commercial solvers. The following section describes the two-phase procedure used in the wood drying industry to formulate the model, which is subsequely validated with two commercial solvers. Additionally, the computing time is improved through a process of parameter analysis, and validated by an exhaustive statistical analysis.
II. Methods and materials
The methods were divided into two stages. In the first stage, the products were grouped by density and fiber type, considering a tolerance range of 3 mm of difference in density; the data were obtained from the SAP system of the company; and the loads were composed according to the maximum capacity of the dryer, with each load consisting of 30 lots of the same density and type; however, in some cases, due to optimization of sawmill production, it was not possible to form a load, hence mixtures were formed. In the second stage, the mathematical model was formulated, and sets, parameters, variables, and constraints were defined.
The first stage consisted in grouping products and adjusting loads. To group products, we obtained the history of the sawmill production, which accounted for a total of 69 products. We classified these products into 45 groups, which we assigned to the adjustment of the loads, according to quality conditions.
III. Formulation of the mathematical model
The requirements to formulate the model in the drying area considered ten drying chambers, with a volume dependent on the product type. Chamber technologies were classified into three types: three dryers of UHT, six of ACTH, and one of ACTHDT type. Dryer technologies were differentiated by temperature, processing time, and capacity; and the 69 products, by type and density. The idea is that the maximum capacity of the dryer contains just one type of product to avoid a wood mix up that may alter the drying process. The processing times, according to the type of product and drying, were provided by the management and validated by the times of the drying control system. Products delivered by sawmills cannot be exposed to environmental conditions for more than three days, i.e., the maximum date to enter the dryer is (k + 3), where k represents the product's storage day by drying area. The programming horizon was monthly.
The model was formulated to propose a solution to the problem of production scheduling in the drying area, focused on making the decision of what, when, and how much product to program, and on which machine perform the operation. Sets, parameters, objective variables function, and restrictions were defined.
A. Sets
The model has two sets m and N, where m = {1,..,m} represents the set of available parallel machines, and N= {1,..,n}, the set of jobs, which fluctuates according to the monthly load.
B. Parameters
A set of four parameters were identified for the model. P ij is the process (drying) time of job j in machine i. B ij, the possibility of processing job j in machine i; this paramenter is established by the technology of the dryer, via a compatibility index. Each job has a reception time, denoted by K j that corresponds to the time at which the product is stored in the courtyard prior to starting the drying process. Jobs have an expiration time defined as D j, since, according to the quality standard, the products cannot be exposed for more than three days to the environmental conditions.
C. Variables
The binary type variable takes a value of 1 if it assigns job j to machine i.
C max : Maximum time of completion for all jobs
The continuous decision variable determines the maximum time of completion of the last job j processed on machine i.
f ij : Entering time of job j in machine i
The continuous variable determines the starting date of job j in the dryer.
D. Objective Function
Min = Cmax
The Objective Function establishes that the maximum time of completion of those processes should be minimized.
E. Restrictions
Restriction (1) ensures that each job j can only be scheduled and processed by a single machine i of m available machines. Restriction (2) ensures compatibility and possibility to process job j on each machine i, according to the conditions of each type of dryer technology, i.e., relating each machine i with jobs j. Restriction (3) establishes the maximum competition time (Cmax) as the greatest amount of processing time on each machine. Restriction (4) establishes sequencing of loads, i.e., the time at which job j enters into machine i plus its processing time, which must be less than the entering time of consecutive jobs j into the same machine i for all machine i and every job j. Restriction (5) refers to the entry time of job j into machine i, establishing when job j is assigned to machine i; the entering time of this job j into machine i must be greater than or equal to the time when j was received; this is for all i belonging to the set M of machines and all j belonging to the set N of jobs. Restriction (6) assures that time of job j entering into machine i does not exceed job j maturity time, when assignation occurs; this is for all i belonging to the set M of machines and for all j belonging to the set N of jobs. Restriction (7) defines the nature of the decision variable, being of binary type. Restrictions (8) and (9) establish the non-negativity of the variables. The L parameter corresponds to a very large, but finite number according to the Big M method.
IV. Results
All experiments were processed on a computer with 4 GB RAM, processor Intel Core i5, model 3570, 3.4 GHz, Windows 7 Professional 32-bit. The model was implemented in AMPL [20], executing 108 combinations of instances and parameters.
A. Scheduling of parallel machines
Manually programming of the ten dryers, in a horizon of six days, resulted in a makespan of 132.23 hours; whereas, programing with the proposed model resulted in a shorter makespan of 121 hours, that is, an improvement of 8.5 %. Moreover, the model decreased the dead time from 454 to 203 hours, and increased the total loads from 31 to 38 loads for the first week of the horizon analyzed.
B. Solver analysis
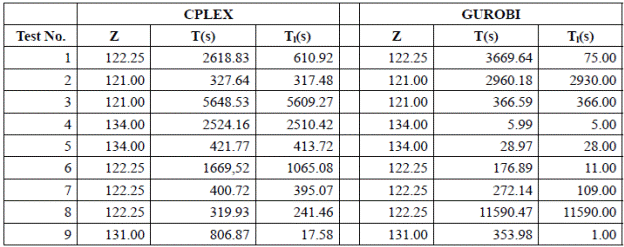
To analyze the parameters that impact the computing time, nine instances were generated, with computing times ranging from 300 to 5000 (s) and from 6 to 11000 (s), in CPLEX version 12.6.3.0 and GUROBI 6.5.0, respectively. Table 1 presents the instance, objective function value (Z Value), time resolution (T (s)), and last improvement time (T1(s)) for both solvers.
Fig. 1 shows the evolution of the upper dimension (Whole Solution) and the lower dimension (Best Bound) for instance No. 1. Upper and lower domensions slowly converge, accounting for most of the improvements for the whole solution (Incumbent) in the first explored nodes, after which, it is only necessary to enumerate nodes up to achieving to close the difference between both levels (GAP), and thus obtain the optimal certificate for the solution, producing only minor improvements in the last nodes.
C. Analysis of parameters with CPLEX and GUROBI
108 instances and parameter combinations were executed to record times, and to comparatively study the GUROBI and CPLEX parameters. In CPLEX, the following parameters were assessed: Mipcuts evaluated at (-1), i.e., does not generate cuts, and Mipcuts evaluated at (2), i.e., aggressively generates cuts. Mipemphasis (0) emphasizes feasibility over optimality, and Mipemphasis (2) emphasizes optimality over feasibility. Repeatpresolve (0) deactivates, represolve (3) repeats pre-processing of the root node and allows new cuts. In GUROBI, Cuts evaluated at (0) does not generate cuts, and Cuts evaluated at (3) aggressively generates cuts. Mipfocus (1) emphasizes feasibility over optimality, and Mipfocus (2) emphasizes optimality over feasibility. Presolve (0) disables the preprocessing of the model, and Presolve (2) pre-processes the model in a more aggressive way.
The computing times (s), according to each parameter, are shown in Table 2; tests are bounded by 3600 (s), and thus avoid significant deviations stemming from excessive times.
D. Statistical analysis
The statistical analysis was performed via hypothesis testing, using the difference between the base model and each parameter; the null and alternative
hypotheses were defined as H 0 =μ1 ≤ μ2 and H 1 =μ1 > μ2, respectively.
Table 3 summarizes the statistical analysis. The only case in which the parameter mean is less than the base model is repeatpresolve valuated at zero for the rest of the cases. The null hypothesis is accepted, therefore, there is no statistical evidence that the averages of the parameters in the evaluated models have less times than the basic model of each solver.
E. GUROBI vs. CPLEX analysis
All instances were resolved with feasible solutions for the problem of scheduling parallel machines. CPLEX solved more instances to the optimum. The time of the parameter of CPLEX repeatpresolve is emphasized; in deactivated mode, it records the lowest time in most of instances.
F. Analysis of cuts with CPLEX and GUROBI
The average time of the Mipcuts parameter evaluated at -1 was 1041.00 (s), and two of the nine instances failed to be resolved to the optimum. When evaluating the parameter at 2, the average time was 924.88 (s), and only one of the nine instances failed to be resolved to the optimum. As for time and number of decisive instances, conducting aggressive cuts yielded better results.
In GUROBI, the cuts parameter in deactivated mode worked slightly better, recording a time average of 714.86 (s) with only a single instance not resolved.
Evaluating the parameter at 3 resulted in an average time of 2422.80 (s), with five instances failing to be resolved to the optimum.
G. Analysis of Mipemphasis and Mipfocus with CPLEX and GUROBI
In CPLEX, with the Mipemphasis parameter evaluated at 1, the average time increased by 31.72 %, and four instances did not converge to the optimum. When evaluating the parameter at 2, the time average was reduced by 17.3 %, and three instances did not obtain the optimum. On GUROBI, with the Mipfocus parameter evaluated at 1, the average time increased by 29.43 %, in addition, nine of six instances failed to resolve to the optimal. For the case of evaluating the parameter at 2, the time average fell by 20.37 %, and two instances did not resolve to the optimum.
Notably, with the Mipemphasis parameter evaluated at 2, for a group of instances (2, 3, 4, 5, 7), times declined considerably. Moreover, in instances 3, 4, and 5, the problems resolved almost instantly.
H. Analysis of Presolve with CPLEX and GUROBI
The parameter repeatpresolve evaluated at zero recorded an average of 414.14 (s) and all instances resolved to the optimum; the best being the basic CPLEX model, with a decrease of 75 % in the resolution average time. For this case, with a level of significance of 0.05, the null hypothesis is rejected, statistically supporting that the basic CPLEX model has times of resolution higher than the repeatpresolve (0) model. Evaluating the parameter at 3, genereated 6 instances that did not resolve to the optimal, and an average computing time that raised to 2671.35 (s).
In GUROBI, evaluating the Presolve parameter at zero generated six unresolved instances to the optimum, and an average time of 2074 (s). When assessing the parameter at two, the aggressive reformulations and cuts on the root node helped solving the problem, resulting in a single instance that could not be resolved to the optimum, and a considerable decrease in the average time to 740.18 (s).
V. Conclusions
Regarding the execution of the model, we obtained favorable results for the input of 38 loads. Applying the model, the dead times decreased to 203 hrs and a total of 38 loads for the first week of December, according to the data of the dry area. With manual programming, however, based on the data downloaded from the control system of the dryers, a dead time of 454 hrs and a total of 31 loads were obtained. We can conclude that implementing a model of production programming positively influences the productive process.
When the size of the instances is superior to 38 loads, the model increased the computing time; quick solutions of good quality to resolve these cases exist; however, the greater amount of time is used to demonstrate that this is the optimal solution. We conducted an experiment to find out which parameters can improve this behavior; for this, we analyzed two types of solvers, CPLEX and GUROBI.
Of the 108 instances executed in AMPL and the 54 CPLEX instances, 60 % experienced improvements regarding time. As for the 54 instances in GUROBI, only 33 % improved the behavior of the model. Furthermore, CPLEX achieved more instances resolved to the optimum, which leads us to conclude that the solver CPLEX is better than the solver GUROBI, in terms of the number of instances resolved.
Regarding the average of each parameter, the only one that presented improvements was repeatpresolve in deactivated mode, which considerably reduced the computing times. Also, in the hypothesis testing, repeatpresolve in deactivated mode was the only parameter whose average differences were significant.
VI. Recommendations and future work
The model showed symmetry given more than one machine with the same technology, and therefore, it presented equal processing times. We suggest exploring new formulations based on representatives and cut planes that actively exploit this condition to improve computing times. In the future, heuristic techniques based on mathematical models (math-heuristics) could help to reduce computing time and efficiently explore the solution space.