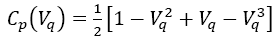I. Introduction
Energy efficiency has always been important in the modern world, especially nowadays given that non-renewable resources are in decline, and in many countries around the world, energy hopes are based on renewable resources such as solar, wind, thermal, oceanic and biomass, which are increasingly exploited using new and modern technologies [1,2,3,4,5,6].
In the case of wind industry, its growth in recent years has been so great that by the end of 2017 it reached a total installed capacity of 539,123 GW, according to the Global Wind Energy Council (GWEC) [7]; countries such as China, USA, Germany, India, Spain, United Kingdom, France, Canada and Brazil have increased considerably their installed capacity in the last years. Wind farms are being built both on shore and off shore, so the growing and importance of wind energy now and in the future is undeniable.
In Wind Energy Conversion Systems (WECS), the power coefficient is an element of great importance; its understanding, representation and estimation have been thoroughly investigated over the years due to the impact on the exploitable wind energy. Even in the early 1920's, Betz established a limit for power coefficient (Cp) known as Betz limit, which has been subject of analysis ever since [8,9,10,11,12]; moreover, important advances in wind energy technologies have been made in recent years, and several research dealing with emerging technologies have already been published [13].
The power of the wind affects the blades of a wind turbine, but not all the power can be extracted. There are many factors to be considered in order to establish an adequate treatment for analyzing this phenomenon. By definition, the power coefficient in a wind energy conversion system is the fraction of the wind energy that is extracted by the turbine. Therefore, it is very important to analyze the behavior of the power coefficient, given that this is a topic where energetic efficiency is being managed.
The study of Cp allows finding the point to maximize wind power extraction according to the speed of the wind. Once the value of tip speed ratio that maximizes Cp is determined, the speed of the generator's rotor can be set by an appropriate control system that allows to obtain the maximum possible Cp for a certain wind speed; however, this is not the goal of this work.
Many equations have been developed to represent Cp, as well as some observers to estimate its behavior depending on the tip speed ratio, but all of them are just approximations of the real shape of Cp. Cp is not easy to be determined and it changes over time due to real conditions of the system, such as mechanical wear, heating and atmospheric conditions, hence the importance to develop models to represent or to estimate Cp.
Previous studies have reviewed the estimation of wind speed based control on wind turbines, based on polynomial estimation, neural network estimation and nonlinear estimations with Newton Raphson [65]. Other studies have presented an overview of general aspects related to WECS as an introduction that provides general information to the readers [14], and of exponential, sinusoidal and algebraic representations for power coefficient [17, 20, 43, 44], failing to include estimators by state observers and own proposals for modeling Cp.
Consequently, and given the scarcity of studies, the context of this investigation turns around the importance to present an overview of representations and estimators of Cp to provide the reader a summary material of this remarkable topic. We hypothesize that a paper that exhaustively reviews the literature on the representations and estimators of the Cp in wind turbines will allow researchers, students and even non-experts in the field of wind energy to understand the behavior of the Cp in wind energy conversion systems, saving time and supporting their investigations.
Here, we summarize the results of most studies related to representations of Cp, such as sinusoidal, exponential and algebraic models; however, these representations only have an acceptable behavior in a certain zone of tip speed radio. On the other hand, there are few estimators of state observers; these models are more complex but better to show the behavior of Cp. After the introduction, we present general aspects such as the definition of Cp and Betz limit, followed by the exponential, sinusoidal and polynomial representations of Cp according to many authors, and the observers and alternative models for Cp. Subsequently, we describe the results and discuss them, and compare the advantages and disadvantages of Cp representations. Finally, we present conclusions and references.
II. Methods
This section presents general aspects of power coefficient such as its definition and characteristic equation. It also shows representations and estimators of Cp, and alternative models based on the stochastic function of probability.
A. General aspects of power coefficient (Cp)
When studying a wind turbine, a typical model considers the system like an ideal, conic and closed tube, which means flow is the same along the tube (Figure 1), so flow conservation law is applied [15, 16] (1).
Where S1, S and S2 represent cross-sectional area upstream, in wind turbine and downstream, respectively. V1, V and V2 represent wind before, on, and after the turbine, respectively. By definition, the power coefficient in a wind turbine is given by equation (2).
where P is the power of the wind and P1 the power extracted by the turbine. Betz demonstrated in 1919 that the maximum value of Cp to be obtained is 0.593; nevertheless, some results that apparently have over exceed Betz limits have been reported [8, 9]. Expression (2) may be expressed as equation (3).
B. Representations of Cp
In actual wind systems, the left section of Cp is different to that shown in Fig. 2. In practice, the limit of Cp when Vq tends to zero is zero because, in that case, V1 is zero, therefore, there is no wind power to be extracted. Throughout the years, research has focused on obtaining functions that better represent the real graph of Cp; some of them are the sinusoidal, exponential and algebraic representations [17].
1) Exponential models: They have been very commonly used in the literature [18,19,20,21,22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36,37,38,39], all of them adjusted to the general structure given by expression (4).
Where λ represents the tip speed ratio, β is the pitch angle, and γ is defined by equation (5).
Different values of coefficients are used depending on the authors (Table 1). Naturally, the complexity of the calculations, as well as the differences between the curves of Cp, are related to the number of coefficients considered in the function defined for Cp. The negative behavior of curves shown in Fig. 3 were suppressed by programming code.
2) Sinusoidal model: Several authors have proposed a model for Cp using sinusoidal functions, so the curves are partially similar to the shape of Cp [40,41,42,43]. The general model is shown by expression (6).
Different values for coefficients ai and bi have been proposed (Table 2).
Fig. 4 shows the Cp curves for every proposed coefficient. Negative values of Cp are suppressed by programming code. The differences among the Cp curves mostly depend on the angle of the function sine.
3) Polynomial model: This is a very well-known model for representing Cp, which curve is generated by equation (7). Nevertheless, eventually, this curve tends to either positive or negative infinity. The complexity of the calculations is naturally related to the number of coefficients used in the model. Four polynomials cases have been proposed by different authors, as well as a particular case that was developed in this paper [43,44,45,46]. Table 3 shows the proposed coefficients, and Fig 5. the curves.
Different curves generated by (7) accordingly to the proposed coefficients shown in Table 3 are illustrated in Fig. 5. Negative values of the curves proposed in [45, 46] were suppressed by programming code.
Noteworthy, the function proposed in this paper is perfectly adjusted along typical values of λ, it fits the practical limits of Cp when λ tends to zero and is into the Betz limit. Coefficients were obtained through mathematical analysis by linear regression using MATLAB. Differences among the curves of Cp depend on the power of the polynomial and the coefficients associated to the terms.
C. Estimators of Cp
Several studies have concentrated on estimating the curve of Cp through state observers [47,48,49,50,51,52,53,54,55,56,57,58,59,60]. Certainly, wind turbine manufacturers usually provide a Cp curve, but it eventually changes due to mechanical stress, friction or system robustness. The change in Cp causes undesirable results and difficulty in controlling the system appropriately [61,62,63].
1) Continuous state observer: Some researchers have proposed dynamic models to estimate Cp. In [50], a continuous state observer is proposed to estimate Cp in a wind turbine connected to a separately excited dc generator to facilitate maximum power point tracking control design as shown in (8).
Where ω is angular speed, Cp power coefficient, ρ air density, R rotor radius, u wind speed, J inertia, γ transmission gear ratio, K1 induced emf constant, if field current, ia armature current, B turbine frictional constant, Ө angular position, l1 , l2 observer constants, RT armature + load resistance and LT armature + load inductance. Two advantages of this observer is that it is capable of handling measurement noise, and it can also have been applied to other WECS where different kinds of generators are used.
2) Alternative models: Some original models [64] have also been proposed to represent the Cp curve such as expressions (9) and (10).
On one hand, Figure 6 shows the associated curve to expression (9), which has the advantage of having a limited magnitude of Cp, even for values of λ that are outside of the experimentally feasible limits. This expression is similar than that used as a stochastic function. On the other hand, it can be observed in Figure 7 the related curve to expression (10) which has a bias factor that allows a better approximation to the real Cp curve.
III. Results and discussion
After reviewing the literature about representations and estimation of Cp, we found an important variety of models, whose advantages and disadvantages are summarized in Table 4. In the case of the representation of Cp by a polynomial of 4th grade, the results were obtained using the mathematical software MATLAB, establishing the equations to solve different coefficients of this polynomial by considering a symmetrical response of Cp. Several approximations were made before obtaining the most suitable coefficients for the 4th grade polynomial, keeping the values of Cp under Betz coefficient.
Moreover, we obtained alternative models through heuristic tests based on the stochastic function of probability. We obtained good results in values of Cp even in the regions beyond the operation zone of tip speed ratio, so this is the relevance of this representation for Cp. As there are few studies about representations and estimations of Cp, one of the relevancies of this work is to show these models after doing an exhaustive bibliographical research, which constitutes the main strength of this work.
IV. Conclusion
Based on the available literature, several models have been proposed to describe Cp, but they are only approximations and usually present problems representing Cp for values out of the typical zone of tip speed radio, especially exponential, sinusoidal and polynomial models. For estimating Cp by state observers, curves of Cp are more accurate, but they imply a considerable increase in complexity and calculations. All these models present values of Cp lower than the Betz limit of 0.593.
An analysis of the behavior of alternative models showed that they presented an accurate approximation to the real Cp curve for values of tip speed ratio above the typical zone; they may be an important alternative for representing Cp, however, the first one presents a maximum value of just 0.17 for Cp, while the second is above the Betz limit.
After reviewing the state of the art, we found only few studies about power coefficient estimation, so it still constitutes an important field worthy to be studied. It may be a trend topic in the near future.
Author's contribution
J. G. González Hernández: reviewing of the state of the art, analysis of information, experimental tests, programming, generation of tables and graphics. R. Salas Cabrera: supervisor of the research, reviewer of structure and syntax, critical analysis of the information and approval of results.