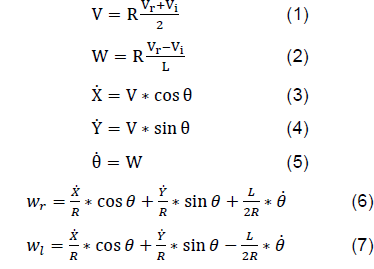I. INTRODUCTION
Generally, studies on trajectory tracking of mobile robots are based on classical mathematical models described in the literature, which represent in a very simplified way the kinematics of the robot, such as [1, 2]. In some cases, mathematical equations are included that roughly represent the dynamics of the system [3]. These equations work relatively well when the system is linear in a specific range, as proposed by Alves [4], the mathematical model of the motors of the traction system is only obtained from physical laws, so the model may present low accuracy when there are many variations of the system dynamics over time, uncertainty or disturbances.
Related works try to solve this problem in different ways, some authors focus on analyzing the impact of parametric uncertainties of a kinematic model on the estimation of the speed and pose of the robot, which provides important information for the design of the controllers [5]. Abdelwahab [6] presents a rule-based heuristic control system with fuzzy logic, which has proven to be useful in addressing uncertainty and imprecision to achieve robust and smooth trajectory tracking. Ortigoza [7] also proposes as a strategy to develop models and controllers for each subsystem that makes up the robot, including the power stage. Dobribarsci [8] proposes the identification of motors up to the design of linear and non-linear controllers. In these and other articles it is common that the models obtained do not include updates over time.
The objective of the research is to present a methodology for the identification, modeling and optimal control of a mobile robot in trajectory tracking tasks [9], for which online identification is performed, that is, the model is being updated in real time, constituting a significant contribution to making the model and robot controllers more accurate. A discrete-time parametric model is used, among which the autoregressive model with exogenous variable ARX [10, 11] stands out.
This article is structured as follows: section 2 describes the hardware, software and methodology used for identification, mathematical modeling and control, section 3 presents the results and analysis, section 4 presents the conclusions.
II. MATERIALS AND METHODS
This section describes the hardware and software materials, and the methodology for identifying, modeling, and controlling the robot for trajectory tracking missions.
A. Mobile Robot
With the Lego Mindstorms EV3 [12] educational kit, a differential locomotion mobile robot was built, as shown in figure 1.
C. Identification, Modeling and Control
1) Direct Kinematics of the Mobile Robot. To obtain the kinematic behavior data of the differential robot, it is assumed that the robot moves on a flat surface without friction, that it moves only by the rotational motion of the wheels, that it is considered as a solid, rigid mechanism without flexible parts, but that the holonomic constraints of the system must be considered [13-14], that is, it cannot move to the sides, as shown in figure 2.
The measurements of interest in the modeling process are the distance between the wheels, called L and the radius of the wheels, called R, as shown in figure 3.
To achieve precise movement, control must be exercised over the right and left wheel velocities, VR and VL, which affect the states of the system x, y, θ. The robot's linear and angular velocities are defined in equations (1) and (2), from which equations (3), (4) and (5) define the kinematics of the robot's motion on each axis.
Where v is the linear velocity, θ is the angle of orientation,
 and w are the angular velocity. Equation (8) denotes the kinematic of the vehicle's motion. With the direct kinematic model of the robot, the control system for tracking the trajectory is developed.
and w are the angular velocity. Equation (8) denotes the kinematic of the vehicle's motion. With the direct kinematic model of the robot, the control system for tracking the trajectory is developed.
2) Inverse Kinematics of the Mobile Robot. To control the movement of the robot, the angular velocities of the robot wheels are altered, which are determined from the desired linear and angular velocities, which are represented by equation (9).
3) Motors Identification, Modeling and Control. For the modeling of the engines, an on-line identification method is used, with a recursive least square RLS algorithm and autoregressive parametric model with exogenous variable ARX of first order. For each motor, a self-adjusting PID adaptive controller is implemented in pole assignment. The RLS algorithm constantly updates the ARX model of the motors and the parameters of the adaptive controllers, allowing more accurate system response. Each motor control transfer function is shows in equations (10) and (11) and their Simulink implementation is shown in figure 4.
In this representation, the position error vector
This error corresponds to the robot's reference system
 , where
, where
 , are the coordinates of the target. If α Є I, where:
, are the coordinates of the target. If α Є I, where:
Applying transformation to polar coordinates considering as its origin the objective point, we obtain:
Where p is the distance between the moving robot and the target, α is the angle needed to orient the robot towards the target point. Finally, β is the angle of orientation of the robot with respect to the coordinate system of the target point.
The task of controller design is to find a control matrix, which is given by equation (17), in equation (18) the control action is expressed.
4) Trajectory Tracking Control. For the trajectory tracking is proposed a Lyapunov control algorithm, based on the robot kinematic model, to generate the signals of the speed and orientation angle, with which the mobile robot is intended to follow the coordinated points x and y of the reference trajectory previously described in Matlab and transmitted via Wi-Fi from the computer. Figure 5 shows the kinematic parameters to be considered between each point of the robot's trajectory. Equations (19) and (20) represent autoregressive models with exogenous variable for each motor.
Figure 6 shows the implementation in Simulink of equations 14, 15, 16, and the path generator in the Matlab function block.
For the modeling and simulation of the trajectory points tracking control of the mobile robot, equations (19) and (20) for the linear and angular speeds control of the mobile robot were implemented in Simulink. Figure 7 shows the result of the validation and simulation of the trajectory tracking by Lyapunov.
Figure 8 shows the forward and inverse kinematics of the differential drive robot.
III. RESULTS AND ANALYSIS
The figure 9 shows the trajectory tracking results of the real robot, there is a certain margin of error at the beginning of the trajectory of the mobile robot, this is due to the initial values present in the matrix k, equation (17). For the circular trajectory, where the robot starts from position (0,0), and 0° orientation degrees, it is observed that the robot requires more time to reach the desired trajectory, the opposite happens for the straight-line trajectory, it influences the computational expenditure by the processing system and energy consumption by the traction system. Table 1 shows the criterias of the error integral [15] used for selecting the PID adaptive controller. the controller that has the best results is the self-adjusting adaptive in pole assignment.
Tabla 1 Selection criteria PID self-adjusting adaptive controller.
| Motor | Criteria | Self-adjustable controller in phase margin | Self-adjusting controller in pole allocation |
|---|---|---|---|
| A | IAE | 29.57 | 1.829 |
| ICE | 736.3 | 17.31 | |
| IAET | 15.64 | 0.077 | |
| D | IAE | 29.65 | 1.798 |
| ICE | 736.8 | 17.16 | |
| IAET | 15.73 | 0.104 |
IV. CONCLUSIONS
The methodology of identification, modeling and control presented in this article allows the permanent online update of the locomotion system engine models, as well as the parameters of the controllers designed to track the trajectories of the differential drive robot, which is an advantage because it achieves more accurate system response compared to traditional identification, modeling and control techniques that have a limited range of operation.
The online identification method implemented allows knowing at any instant of time the mathematical model of the motors, an aspect that is not possible in those techniques where the model is only obtained from physical laws.
The online parameters update of the trajectory tracking controllers, allows movements with precision and smoothness, compared to results obtained with the classic PID controllers evaluated. The execution of smooth trajectories is associated with less control effort and lower energy consumption [16].
The implementation of controllers from the Lyapunov stability analysis, facilitates to the system to work optimally in the event of unexpected changes or disturbances, consequently, the robot may have a better cost-benefit ratio in energy consumption, smoothness of the trajectory, precision of movements, etc.
The proposed methodology provides a strategy to solve path and trajectory tracking control missions. Simulations and experiments were performed in real environments to verify their robustness and efficiency. In addition, taking mathematical models to first-order systems favors the low computational cost of the proposed solution.