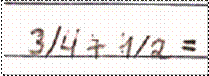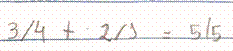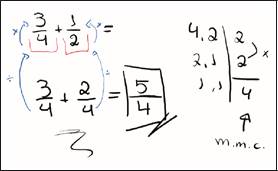Introdução
De acordo com os Parâmetros Curriculares Nacionais de Matemática do Ensino Fundamental - PCN (Brasil, 1998), é importante utilizar estratégias de ensino que se distanciem da forma tradicional de ensinar. Tal documento incentiva, por exemplo, o uso da resolução de problemas no ensino de Matemática. No PCN aponta-se que o problema deve ser o ponto de partida e não a definição matemática, destacando que:
o problema certamente não é um exercício em que o aluno aplica, de forma quase mecânica, uma fórmula ou um processo operatório. Só há problema se o aluno for levado a interpretar o enunciado da questão que lhe é posta e a estruturar a situação que lhe é apresentada. (Brasil, 1998, p. 41)
No Brasil, alguns estudos que realizaram e analisaram propostas de ensino no viés do uso do problema como ponto de partida para abordar um novo conteúdo revelaram que: apesar de dificuldades de alunos dos ensinos fundamental e médio no uso de seus conhecimentos matemáticos, aprendidos anteriormente, o trabalho feito em sala de aula propiciou condições para que esses alunos desenvolvessem estratégias e, assim, pudessem associá-las ao novo conteúdo que estava a ser aprendido (Vieira et al., 2013; Sousa e Proença, 2019; Vargas e Noguti, 2020; Oliveira e Proença, 2020).
Vieira et al. (2013) abordaram a simetria de reflexão pela introdução de uma situação-problema, envolvendo a palavra “RESGATE”, escrita na parte frontal da ambulância. Os dados mostraram que os 37 alunos do sétimo ano do ensino fundamental, ao resolvê-la, utilizaram duas maneiras: invertendo apenas a palavra; e invertendo a palavra, mas também invertendo as letras.
Sousa e Proença (2019) abordaram a equação de 1º grau com uma incógnita pela introdução de duas situações de Matemática, sendo a primeira do tipo partilha e a segunda do tipo transformação. Os resultados mostraram que, dos 34 alunos de sétimo ano do ensino fundamental, a maioria dos sete grupos adotou a estratégia “tentativa e erro” para resolver os dois problemas. A estratégia “montar tabela” só foi utilizada no primeiro problema e por três grupos, o que, neste caso, contribuiu para a generalização e associação a uma equação de primeiro grau. Durante a pesquisa, as dificuldades dos alunos decorreram do uso do conceito de dobro, triplo e igualdade.
Vargas e Noguti (2020) abordaram a progressão aritmética pela introdução de cinco problemas. Os resultados mostraram que os 38 alunos do primeiro ano do ensino médio tiveram as seguintes dificuldades: na compreensão da expressão algébrica, fazendo substituição indevida das variáveis; nos cálculos necessários, fazendo divisão antes da subtração. No entanto, apontou-se que os alunos demonstraram interesse nas discussões e reflexões durante a sistematização do conteúdo.
Oliveira e Proença (2020) abordaram a Matemática Financeira, referente ao conteúdo de acréscimos e descontos, pela introdução de uma situação Matemática. Os resultados mostraram que os 44 alunos do terceiro ano do ensino médio tiveram dificuldades na elaboração de uma estratégia, porém, com o auxílio da professora-pesquisadora, puderam propor e utilizar três estratégias: equação de primeiro grau; equação de primeiro grau, usando frações; regra de três.
Nesse sentido, utilizar o problema como ponto de partida pode ajudar os alunos a focarem sobre o processo de resolução de problemas e na construção de conhecimentos e não simplesmente na aplicação direta do conteúdo apresentado pelo professor (Fi e Degner, 2012; Lester e Cai, 2016; Proença, 2018; 2021). Torna-se importante, assim, realizar mais estudos com sugestões de propostas de ensino em outros conteúdos matemáticos para revelar as dificuldades inerentes. Um conteúdo seria o que envolve a operação de adição de frações, para o qual não encontramos estudos sobre o assunto com uso do problema como ponto de partida, desenvolvido em sala de aula. Diante disso, o objetivo desta experiência de caso educativo foi compreender a contribuição de um ensino da operação de adição de frações via resolução de problemas para o aprendizagem dos alunos.
Fundamentação da experiência
A nossa experiência de caso educativo seguiu os pressupostos teóricos da abordagem de Ensino-Aprendizagem de Matemática via Resolução de Problemas (EAMVRP), proposta por Proença (2018), a qual adota o uso do problema como ponto de partida, e que envolve cinco ações de ensino: escolha do problema; introdução do problema; auxílio aos alunos durante a resolução; discussão das estratégias dos alunos; articulação das estratégias dos alunos ao conteúdo.
Escolha do problema
Esta primeira ação implica na escolha de uma situação de Matemática (possível problema). O professor pode fazer essa escolha, obtendo-a na íntegra, sendo reelaborada, sendo elaborada ou com foco em tratar de um padrão algébrico. Junto a isso, Proença (2018) indica que sejam elencadas possíveis estratégias de resolução, as quais podem ajudar a resolvê-la, tais como tentativa e erro, fazer figuras, desenhos ou diagramas, montar tabelas e a de utilizar casos particulares para, no processo de generalização, encontrar um padrão. O ponto principal de realizar essa escolha e de elencar estratégias é dar condições aos alunos para poderem utilizar seus conhecimentos prévios de Matemática, de modo que no final possa articulá-las à forma matemática do novo conteúdo a ser estudado. No âmbito escolar, induzir os alunos a pensarem em conceitos e procedimentos matemáticos que já aprenderam, contribui com a formação de ideias matemáticas que possam ser utilizadas, por exemplo, na construção de equações matemáticas, de conceitos matemáticos e outras ideias, proporcionando, então, uma relação entre seus conhecimentos prévios e os que estão sendo trabalhados.
Introdução do problema
Esta segunda ação de ensino refere-se ao contato do professor com os alunos, em que lhes apresentará a situação de Matemática escolhida. Dividir a turma em grupos menores é uma atitude incentivada por Proença (2018) porque possibilita que cada grupo socialize opiniões e argumentos para proporem suas estratégias de resolução, bem como possibilitará ao professor discutir, nas próximas ações, suas ideias. Assim, Proença (2018) explicou que é nesta ação e nesse envolvimento em grupos pequenos que o contato inicial com a situação de Matemática pode tornar-se um problema, de modo que:
no caso da Matemática, entendemos que uma situação de Matemática se torna um problema quando a pessoa precisa mobilizar conceitos, princípios e procedimentos matemáticos aprendidos anteriormente para chegar a uma resposta. Não se trata, assim, do uso direto de uma fórmula ou regra conhecidas - quando isso ocorre, a situação tende a se configurar como um exercício. É importante relembrar que a função de um exercício no ensino é justamente que o aluno aplique fórmulas, regras, algoritmos, que siga modelos. (Proenca, 2018, p. 17-18)
Auxílio aos alunos durante a resolução
Esta terceira ação implica na postura do professor como observador, incentivador e direcionador sobre o que os alunos fazem, voltada a favorecer e apoiar suas aprendizagens, segundo Proença (2018). Este autor explicou que, quando algum grupo não consegue pensar em alguma estratégia de resolução, um direcionamento do professor pode ser o de dar dicas ou de fazer questionamentos que o direcione a uma estratégia que foi elencada na primeira ação, a de escolha do problema. Dessa forma, não se trata de apresentá-la de forma integral e sim de incentivar, por exemplo: que tal pensarem em montar uma tabela, organizando os dados? Que tal fazer um desenho? Além disso, como observador, o professor deve avaliar/analisar os grupos no processo de resolução de problemas. Proença (2018) indica que o professor deve (deveria) avaliar os grupos nas quatro etapas de resolução de problemas, a saber: representação; planejamento; execução; monitoramento. A representação envolve a compreensão do problema pelo aluno, devendo mobilizar seus conhecimentos linguístico (língua materna) e semântico (matemáticos). Nesta etapa, estudos como o de Guérios & Ligeski (2013) e Proença et al. (2020) revelaram que se trata da principal etapa de resolução de problemas, pois mostraram que, respectivamente, 33 e 111 alunos brasileiros de nono ano do ensino fundamental tiveram como dificuldade maior a de uso de seus conhecimentos matemáticos, o que pode dificultar a proposição de estratégias adequadas. O planejamento implica de o aluno apresentar um caminho, isto é, uma estratégia de resolução, a qual pode ocorrer dependendo de seu conhecimento estratégico. A execução consiste do aluno executar sua estratégia, o que exige uso de conhecimento procedimental, ou seja, realizar os cálculos e desenhos envolvidos. Por fim, o monitoramento implica de o aluno avaliar a resposta encontrada, segundo contexto do problema, e mesmo rever a resolução seguida para identificar se está adequada.
Discussão das estratégias dos alunos
Esta quarta ação implica na socialização das estratégias utilizadas pelos grupos. A sugestão é que o professor peça a cada grupo que um representante exponha e explique em lousa como resolveram o problema. Apesar do foco ser para as estratégias, cabe ao professor avaliar e comentar sobre as dificuldades envolvidas no processo de resolução de problemas, levando-os a entender em que consistiram os erros. Dessa forma, ao se envolverem nas etapas de resolução de problemas, conforme as abordadas por Proença (2018), e passando a compreender tais erros, cria-se um ambiente que propicia aos alunos desenvolverem seus conhecimentos e, assim, conforme mostraram Krutetskii (1976) e Triana (2005), desenvolverem habilidades matemáticas para resolução de problemas matemáticos como, por exemplo, o uso consciente de estratégias e o pensar por meio do processo de generalização.
Articulação das estratégias dos alunos ao conteúdo
Esta quinta e última ação tem como foco tomar como referência uma ou mais estratégias apresentadas e, assim, utilizar pontos principais e relacioná-los ao novo conteúdo matemático que está a ser introduzido. Na hipótese de não haver a possibilidade para uma articulação, pode-se apenas demonstrar a forma de resolução matemática desse novo conteúdo. Os estudos de Sousa e Proença (2019) e Oliveira e Proença (2020) seguiram o EAMVRP e, nesta ação de articulação, apenas no segundo problema de Sousa e Proença (2019) não foi possível estabelecer uma articulação.
Descrição da experiência
A experiência de caso educativo se deu pela elaboração de uma proposta de ensino, baseada no EAMARP e suas cinco ações, propostas por Proença (2018), com foco em abordar o conteúdo de operação de adição de frações (cálculo do mínimo múltiplo comum (m.m.c.) e a ideia de “dividir pelo de baixo e multiplicar pelo de cima”) pela introdução de um problema. Implementamos a proposta a uma turma de 10 alunos brasileiros do 6º ano de ensino fundamental de uma escola pública que está localizada no interior do estado do Paraná. O ambiente das aulas ocorreu de forma online pela plataforma Google Meet, devido à época ser essa a forma de aulas permitidas em meio à COVID-19, sendo as aulas gravadas. A seguir, segue a descrição da proposta de ensino.
Escolha do problema
A situação de Matemática escolhida foi obtida na íntegra de Proença (2019, p. 5), a saber: “Sílvio e Lúcio estão participando de uma corrida de bicicleta. Sílvio já percorreu
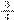 do trajeto e Lúcio percorreu
do trajeto e Lúcio percorreu
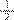 do trajeto. Qual o total percorrido pelos dois juntos?” Assim, conforme indicou Proença (2018), fizemos a previsão de possíveis estratégias que poderiam ajudar a resolver essa situação, as quais, apesar da essência no uso da equivalência de frações, apresentam formas diferentes de execução, conforme abaixo:
do trajeto. Qual o total percorrido pelos dois juntos?” Assim, conforme indicou Proença (2018), fizemos a previsão de possíveis estratégias que poderiam ajudar a resolver essa situação, as quais, apesar da essência no uso da equivalência de frações, apresentam formas diferentes de execução, conforme abaixo:
Estratégia 1
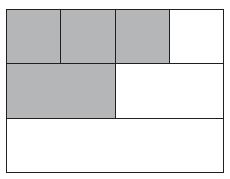
Denominamos por “uso de figura geométrica e equivalência de frações”. Utilizamos três retângulos para situar o trajeto percorrido por Sílvio e Lúcio, bem como situar o todo (inteiro), conforme mostra a Figura 1 abaixo. O retângulo de Sílvio foi representado por 4 quadrados, sendo o seu trajeto percorrido representado por 3 quadrados pintados
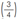 . Já o retângulo de Lúcio foi dividido em 2 retângulos, sendo que o seu trajeto percorrido foi representado por um retângulo pintado
. Já o retângulo de Lúcio foi dividido em 2 retângulos, sendo que o seu trajeto percorrido foi representado por um retângulo pintado
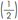 . Por último, o todo, que foi representado por apenas um retângulo em branco.
. Por último, o todo, que foi representado por apenas um retângulo em branco.
Na Figura 1, acima, podemos ver que Sílvio percorreu uma distância maior do que Lúcio. Agora, para sabermos qual é a distância total percorrida pelos dois juntos, é necessário que os trajetos percorridos por Sílvio e Lúcio sejam divididos, ao mesmo tempo, em partes iguais para podermos realizar uma adição, de modo que o todo (trajeto) também seja dividido nessas mesmas partes iguais. Buscamos, em essência, utilizar a ideia de equivalência de frações. Dessa forma, o retângulo pintado que representa o trajeto percorrido por Lúcio
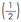 deve ser subdividido de forma a se obter uma fração equivalente, sendo que essa subdivisão seja feita com base nos quadrados do trajeto percorrido por Sílvio. Junto com isso, a subdivisão deve ocorrer em termos do retângulo que representa Lúcio, o que deve ser em quatro quadrados, igual a de Sílvio. Finalmente, podemos obter a fração equivalente:
deve ser subdividido de forma a se obter uma fração equivalente, sendo que essa subdivisão seja feita com base nos quadrados do trajeto percorrido por Sílvio. Junto com isso, a subdivisão deve ocorrer em termos do retângulo que representa Lúcio, o que deve ser em quatro quadrados, igual a de Sílvio. Finalmente, podemos obter a fração equivalente:
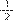 =
=
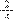 . Assim, o próprio trajeto acaba por ser dividido em quatro partes iguais, o que revela maior clareza da divisão do todo, conforme a Figura 2 a seguir.
. Assim, o próprio trajeto acaba por ser dividido em quatro partes iguais, o que revela maior clareza da divisão do todo, conforme a Figura 2 a seguir.
Uma vez que os retângulos de Sílvio e Lúcio estão divididos igualmente em quatro partes iguais, podemos adicionar todas as partes pintadas, que são cinco, e dividir pelo todo, que é quatro, e teremos o valor total percorrido por eles, o que pode ser feito diretamente da seguinte forma:
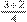 =
=
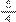 . Caso seja de preferência do solucionador, pode-se fazer a adição com as frações em separado:
. Caso seja de preferência do solucionador, pode-se fazer a adição com as frações em separado:
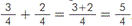 . Assim, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
. Assim, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
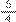 do caminho todo.
do caminho todo.
Estratégia 2
Denominamos de “uso da equivalência de frações”. Com base nas duas frações que constam do enunciado da situação de Matemática, podemos utilizar, diretamente, a equivalência de frações. Assim, devemos perceber que a fração
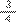 (trajeto percorrido por Sílvio) tem denominador maior do que a fração
(trajeto percorrido por Sílvio) tem denominador maior do que a fração
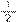 (trajeto percorrido por Lúcio), sendo que esta última fração é que deve ser transformada em uma fração que tenha mesmo denominador da fração
(trajeto percorrido por Lúcio), sendo que esta última fração é que deve ser transformada em uma fração que tenha mesmo denominador da fração
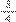 , o que, consequentemente, pelo processo de obtenção de equivalência, implica na mudança de valor do numerador. Para tal, devemos multiplicar numerador e denominador da fração
, o que, consequentemente, pelo processo de obtenção de equivalência, implica na mudança de valor do numerador. Para tal, devemos multiplicar numerador e denominador da fração
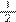 por 2, o que resulta em
por 2, o que resulta em
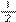 =
=
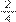 . Diante disso, podemos substituir
. Diante disso, podemos substituir
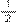 por
por
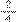 e adicionar a
e adicionar a
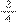 e ter o valor total do trajeto percorrido pelos dois juntos, bastando adicionar os numeradores e manter o mesmo valor do denominador:
e ter o valor total do trajeto percorrido pelos dois juntos, bastando adicionar os numeradores e manter o mesmo valor do denominador:
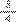 +
+
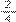 =
=
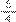 . O denominador é mantido (e não adicionado), porque se trata da divisão do todo (inteiro), ou seja, das quatro partes que o trajeto foi dividido. Assim, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
. O denominador é mantido (e não adicionado), porque se trata da divisão do todo (inteiro), ou seja, das quatro partes que o trajeto foi dividido. Assim, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
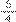 do caminho todo.
do caminho todo.
Estratégia 3
Denominamos de “multiplicação por frações igual a 1”. Utilizamos esse tipo de multiplicação nas frações com objetivo de obter denominadores iguais, o que ajuda a realizar a adição de frações. Este procedimento é similar ao mínimo múltiplo comum (m.m.c.), sendo que a diferença é que não iremos procurar o menor número múltiplo dos denominadores e sim qualquer número em comum. Podemos multiplicar a primeira fração por
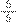 (1) e a segunda fração por
(1) e a segunda fração por
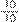 (1), e teremos:
(1), e teremos:
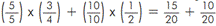 Assim, como obtemos denominadores iguais, podemos adicionar as frações,
Assim, como obtemos denominadores iguais, podemos adicionar as frações,
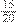 +
+
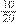 =
=
 , e, em seguida, podemos simplificar por 5, e teremos
, e, em seguida, podemos simplificar por 5, e teremos
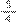 . Portanto, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
. Portanto, a resposta seria: O total percorrido por Sílvio e Lúcio juntos é de
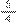 do caminho todo.
do caminho todo.
Introdução do problema
A ideia era propor a divisão dos alunos em grupos, porém, por não conseguirmos estabelecer grupos no recurso tecnológico, cujas falas pudessem ser gravadas, decidimos por projetar a situação de Matemática na tela do Google Meet e, assim, os alunos tiveram que a resolver individualmente. Incentivamos os alunos a resolverem no caderno e pelo caminho que preferissem. A partir do momento que os alunos iniciaram a leitura da situação de Matemática, identificamos dificuldades para propor um caminho, de modo que entendemos que a referida situação se tornou um problema, como Proença (2018) havia previsto.
Auxílio aos alunos durante a resolução
Procuramos não dar um caminho ou apresentar informações que permitissem obter de imediato a resposta. Como os alunos propuseram uma estratégia, apenas os auxiliamos nas dúvidas que surgiram, mas sem dizer se estava certa ou não, pois queríamos discutir os equívocos cometidos e se a estratégia era condizente, na ação seguinte. Ao final desta terceira ação, os alunos escanearam ou tiraram fotos de suas resoluções e as enviaram no grupo Whatsapp criado para recebê-las. Dessa forma, analisamos as resoluções, conforme as quatro etapas de resolução de problemas de Proença (2018).
Discussão das estratégias dos alunos
Nesta quarta ação, pedimos aos alunos que compartilhassem as resoluções pela apresentação por meio do Google Meet, de modo a socializar as estratégias utilizadas. Tanto nesta ação quanto na anterior e na seguinte, buscamos identificar e descrever a participação dos alunos.
Articulação das estratégias dos alunos ao conteúdo
Em nossa proposta de ensino, criamos uma forma de articulação das três estratégias ao algoritmo da adição de frações, elencadas na ação de escolha do problema. Porém, como em sala de aula os alunos utilizaram estratégias voltadas a adicionar os numeradores e denominadores das frações sem saber que isso não pode ocorrer para quando os denominadores são diferentes, apresentamos para eles diretamente (Figura 7) a forma de resolução do novo conteúdo em que pudemos, assim, ajudá-los a entender o motivo dessa da execução dessa estratégia ser equivocada.
Sistematização e análise da experiência
A nossa experiência se insere na vertente de pesquisa de natureza qualitativa, pois envolveu as ações dos alunos no ambiente de aulas que foi pesquisado, sendo, assim, uma pesquisa interpretativa, segundo Bogdan e Biklen (1994). As resoluções dos alunos, as gravações, as observações e as anotações feitas ao longo das aulas constituíram nosso material para posterior análise dos dados. Diante disso, a análise dos dados coletados se deu por meio de dois eixos: a) Dificuldades nas etapas de resolução de problemas - elaboramos um quadro para mostrar as dificuldades dos alunos em cada etapa de resolução do problema, de modo que essas etapas foram definidas a priori. Além disso, apresentamos figuras de suas estratégias para podermos revelar as dificuldades dos alunos nessas etapas;
b) Participação dos alunos - junto às descrições sobre as aulas, apresentamos três quadros para sintetizar a participação dos alunos nas três últimas ações de ensino, cujas categorias de análise foram definidas a posteriori.
Dificuldades nas etapas de resolução de problemas. Neste eixo, ao longo da ação de auxílio aos alunos durante a resolução, o professor-pesquisador constantemente perguntava para os alunos como estavam resolvendo o problema.
Professor: Todo mundo está conseguindo fazer?
A7: Eu não entendi como que faz?
A2: Eu não estou conseguindo fazer, eu não consigo fazer as contas.
Professor: Como que você está tentando fazer?
A2: Eu estou tentando somar as frações, mas eu acho que está errado.
Professor: Tenta fazer dessa maneira, some as frações como você acha que está certo.
A2: Ok, vou acabar e já envio.
Professor: Alguém mais não está conseguindo resolver?
Essa postura do professor em buscar auxiliar os alunos foi identificada no estudo de Oliveira e Proença (2020), na qual mostrou-se que as dificuldades de alunos de ensino médio na elaboração de uma estratégia foram superadas com o auxílio da professora- pesquisadora. Diante disso, ao final dessa ação, o Quadro 1 a seguir mostra as quatro etapas de resolução de problemas e em quais delas os alunos tiveram dificuldades.
Quadro 1 Dificuldades dos alunos nas etapas de resolução de problemas.
| Etapas | Alunos |
|---|---|
| Representação | - |
| Planejamento | - |
| Execução | A1, A2, A3, A4, A5, A6, A7, A8, A9, A10 |
| Monitoramento | A1, A2, A3, A4, A5, A6, A7, A8, A9, A10 |
Fonte: autores.
Sobre a etapa de representação, o Quadro 1 acima revela que não houve dificuldades de compreensão. A nossa observação feita tanto no momento que foi entregue a situação de Matemática aos alunos, quanto no momento de análise de suas folhas de resolução mostrou que foi identificado como eles entenderam que a situação envolvia uma corrida de bicicletas entre duas pessoas, que havia um trajeto a ser percorrido, que se queria saber quanto os dois andaram juntos e, assim, que a situação envolvia uma adição de duas frações.
Referente à etapa de planejamento, verificamos no Quadro 1 que os alunos não tiveram dificuldades para propor uma estratégia de resolução, resultado este semelhante com da pesquisa de Sousa e Proença (2019), a qual mostrou que alunos de sétimo ano de ensino fundamental não tiveram dificuldades em propor uma estratégia. Identificamos que os 10 alunos de nosso estudo utilizou da mesma estratégia, escrevendo a adição das duas frações da forma, conforme ilustramos na Figura 3.
Sobre a etapa de execução, o Quadro 1 mostra que os 10 alunos apresentaram dificuldades para executar a estratégia proposta, o que também ocorreu no estudo de Vargas e Noguti (2020) sobre o conteúdo de progressão aritmética com alunos do primeiro ano do ensino médio, os quais tiveram dificuldades em realizar cálculos envolvendo estratégias para resolver o problema proposto. Identificamos que os 10 alunos do nosso estudo realizaram duas formas de execução, conforme mostra o Quadro 2 a seguir.
Quadro 2 Tipo de execução da estratégia que foi utilizada.
| Execução realizada | Alunos |
|---|---|
| Adicionou os numeradores e os denominadores | A1, A2, A3, A5, A6, A8, A9 e A10 |
| Inverteu uma das frações e realizou a adição dos numeradores e dos denominadores | A7, A4 |
Fonte: autores.
Verificamos que o Quadro 2, acima, mostra que a execução da estratégia, baseada em adicionar os numeradores e os denominadores, foi utilizada por oito alunos, conforme ilustramos na Figura 4:
O aluno A1 executou a estratégia por adicionar os numeradores e denominadores, fazendo 3 + 1 = 4 e 4 + 2 = 6, obtendo, então,
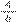 . Dessa forma, verificamos que esse procedimento não é o correto para adição de duas frações, pois não se pode adicionar denominadores diferentes. Consequentemente, os oito alunos que assim executaram essa estratégia não conseguiram (e não conseguiriam) chegar ao resultado correto. Para que a adição ocorresse corretamente, esses alunos deveriam ter buscado, primeiramente, obter denominadores iguais, tendo em vista uma divisão igual do inteiro (todo), conforme evidenciamos nas três estratégias que prevemos.
. Dessa forma, verificamos que esse procedimento não é o correto para adição de duas frações, pois não se pode adicionar denominadores diferentes. Consequentemente, os oito alunos que assim executaram essa estratégia não conseguiram (e não conseguiriam) chegar ao resultado correto. Para que a adição ocorresse corretamente, esses alunos deveriam ter buscado, primeiramente, obter denominadores iguais, tendo em vista uma divisão igual do inteiro (todo), conforme evidenciamos nas três estratégias que prevemos.
Já sobre a forma que se baseou em inverter uma das frações e realizar a adição dos numeradores e dos denominadores, observamos no Quadro 2 que foi feita pelos alunos A4 e A7. Esses alunos inverteram uma das frações e realizaram a adição dos numeradores e dos denominadores, ou seja, inverteram a fração
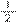 , deixando-a como
, deixando-a como
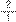 e realizaram a adição
e realizaram a adição
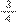 +
+
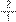 =
=
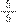 , conforme ilustramos na Figura 5 a seguir.
, conforme ilustramos na Figura 5 a seguir.
Além de terem invertido uma das frações, o que não tem relação com a adição de frações, esses alunos A4 e A7 também erraram ao escolherem adicionar os denominadores, assim como fizeram os demais colegas, o que também os levou a uma resposta incorreta. Esses resultados sustentam o fato de que os alunos dessa turma investigada não conseguiram mobilizar conhecimentos prévios como os de equivalência de frações, que constam das nossas estratégias previstas, entre as quais imaginavamos que poderiam utilizar para resolver a situação de Matemática. Dessa forma, seguindo o ensino e a abordagem do EAMARP de Proença (2018), é possível apontar que no uso do problema como ponto de partida revelou que esses conhecimentos prévios dos alunos ainda não estão bem formados. Isso também mostra que esses alunos terão outras dificuldades em outros conteúdos que exigem operar com frações como as frações algébricas.
Por fim, na etapa de monitoramento, o Quadro 1 mostra que todos os 10 alunos apresentaram dificuldades. Consideramos dessa forma porque tanto nas observações que fizemos ao longo das aulas quanto na leitura que fizemos das folhas de resposta desses alunos, conseguimos entender que eles não buscaram verificar se a resposta estava correta no contexto do problema e também não revelaram atitude para rever a resolução seguida. Possivelmente, pode ser que a execução da estratégia que tomaram como rumo foi entendida realmente como adequada para obter uma resposta, o qual pode ter sido o motivo de não procurar verificar aquilo que fizeram.
Diante desses resultados, entendemos que apesar da estratégia de resolução que foi utilizada ser coerente
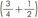 , ficou evidente que os alunos não procuram usos de outras possibilidades de tentativa de busca de uma resposta. Não utilizaram representações por desenho dessas duas frações e nem mesmo a ideia de frações equivalentes, ambas utilizadas nas estratégias previstas, na ação de escolha do problema, conforme o planejamento ao EAMARP (Proença, 2018). A ideia de frações equivalentes, por exemplo, deveria ter sido utilizada pelos alunos, pois é um conteúdo central na Matemática que possibilita realizar a operação aritmética de adição (e de subtração) de frações sem necessariamente usar o algoritmo que envolve cálculo de mínimo múltiplo comum (m.m.c.) e a ideia de “divide pelo debaixo e multiplica pelo de acima”. Assim, as estratégias previstas no EAMARP para adição de frações serviram como forma de dar sustentação ao professor sobre os conhecimentos que os alunos poderiam mobilizar, de modo que foi de nossa escolha não lhes indicar diretamente a essência dessas estratégias previstas e sim olhar para um uso de seus conhecimentos.
, ficou evidente que os alunos não procuram usos de outras possibilidades de tentativa de busca de uma resposta. Não utilizaram representações por desenho dessas duas frações e nem mesmo a ideia de frações equivalentes, ambas utilizadas nas estratégias previstas, na ação de escolha do problema, conforme o planejamento ao EAMARP (Proença, 2018). A ideia de frações equivalentes, por exemplo, deveria ter sido utilizada pelos alunos, pois é um conteúdo central na Matemática que possibilita realizar a operação aritmética de adição (e de subtração) de frações sem necessariamente usar o algoritmo que envolve cálculo de mínimo múltiplo comum (m.m.c.) e a ideia de “divide pelo debaixo e multiplica pelo de acima”. Assim, as estratégias previstas no EAMARP para adição de frações serviram como forma de dar sustentação ao professor sobre os conhecimentos que os alunos poderiam mobilizar, de modo que foi de nossa escolha não lhes indicar diretamente a essência dessas estratégias previstas e sim olhar para um uso de seus conhecimentos.
Além disso, podemos apontar que esses alunos não têm, possivelmente, bem formada a compreensão do que seria o todo e, assim, dificuldades no seu reconhecimento, pois o primeiro conhecimento necessário é sobre o conceito de frações, de modo que deveriam saber que o denominador de uma fração representa as partes iguais nas que o todo (trajeto) foi dividido, não sendo adequado adicionar denominadores diferentes. Essa compreensão errada ocorreu no estudo de Proença (2015) com estudantes de um curso de Pedagogia. Nesse sentido, pode ser que o professor foque em automatizar procedimentos com frações sem recorrer a formas de ensinar (Rojas et al., 2015) como, por exemplo, utilizar apenas exercícios em detrimento do uso de um ensino que seja baseado na resolução de problemas para favorecer a compreensão conceitual. Dessa forma, isso revela que se os professores (futuros) têm dificuldades, possivelmente seus alunos também as terão.
Participação dos alunos
Apesar dessas dificuldades nas etapas de resolução de problemas, identificadas ao final da terceira ação de ensino, acima, foi possível verificar que houve envolvimento dos alunos, de modo que tentaram resolver a situação proposta, conforme mostra o Quadro 3 a seguir.
Quadro 3: Participação dos alunos
| Participação dos alunos | Alunos |
| Não teve nenhuma interação com o professor-pesquisador | - |
| Conversava com o professor-pesquisador pelo chat | A9, A10 |
| Ligava o microfone para conversar com o professor-pesquisador | A3, A4, A5, A6, A8 |
| Ligava câmera e microfone para conversar com o professor-pesquisador | A1, A2, A7 |
. Fonte: autores.
Podemos observar no Quadro 3 que nenhum aluno “não teve nenhuma interação com o professor-pesquisador”. Portanto, todos os alunos se manifestaram com o professor- pesquisador, sendo pelo chat, microfone ou câmera ligada. No caso, a maioria deles, cinco alunos, “ligava o microfone para conversar com o professor-pesquisador”. Isso revela que houve uma disposição dos alunos na procura de uma solução, ou seja, uma participação ativa. Porém, as dificuldades que tiveram revelam indícios de que o ensino que receberam não esteja ou não foi voltado ao favorecimento da compreensão desses alunos sobre ideias como a equivalência de frações e reconhecimento de todo (totalidade).
No caso da ação de discussão das estratégias dos alunos, buscamos socializar as resoluções e, assim, as estratégias dos alunos com toda a turma. Porém, apenas dois deles se disponibilizaram a expor o que fizeram, conforme mostra-se no Quadro 4 a seguir.
Quadro 4: Participação dos alunos
| Participação dos alunos | Alunos |
|---|---|
| Apenas assistiu as explicações dos colegas | A2, A3, A4, A5, A6, A8, A9, A10 |
| Apresentou a estratégia para os colegas | A1, A7 |
Fonte: autores.
Os diálogos abaixo revelam que A1 e A7 apresentaram suas resoluções. A resolução foi transmitida pela tela Google Meet do professor-pesquisador para todos os alunos na sala.
Professor: Vou apresentar para vocês a resolução do A1. Todo mundo consegue ver? A1, explica como você chegou em quatro sextos.
A1: Eu só calculei os dois.
Professor: Como assim? Como você somou?
A1: Eu somei os de cima com os de embaixo.
O aluno A1 utilizou a estratégia de adicionar os numeradores e denominadores das duas frações (Figura 4 atrás), obtendo o resultado incorreto. Já o aluno A7 utilizou a estratégia de inverter uma das frações e adicionar os numeradores e denominadores (Figura 5 atrás), também obtendo resultado incorreto, conforme diálogo a seguir.
Professor: Vamos abrir o de A7 aqui agora. A7, explica para gente como que você fez a adição de frações.
A7: Eu somei os primeiros números das frações (numeradores) e depois os números de embaixo (denominadores). Nesse caso, na segunda fração eu inverti, só que daí eu somei o primeiro de acima. O outro de embaixo da primeira fração de acima da outra.
Professor: Aqui na primeira A7 fez igual com A1, ele pegou o primeiro numerador e somou com outro numerador e deu quatro (3+1=4) e depois ele pegou o denominador quatro e somou com o denominador dois, o que obteve o denominador que deu seis, certo? O A1 e A7 fizeram isso. Aqui embaixo o A7 fez uma segunda opção, ele pegou o numerador do primeiro, e inverteu a segunda fração: era
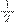 e virou
e virou
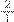 . Ele somou três com dois deu cinco e depois ele somou o quatro com um, o que também deu cinco, resultando em
. Ele somou três com dois deu cinco e depois ele somou o quatro com um, o que também deu cinco, resultando em
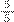 .
.
Destacamos que os resultados do Quadro 3 e do Quadro 4 revelam uma participação dos alunos nas aulas, na maioria das vezes, apenas como expectador e não como ativo, com inciativa de expor sua resolução. Possivelmente, por serem basicamente duas estratégias que foram utilizadas, oito deles não se disponibilizaram a mostrar o que fizeram, o que vai na direção do estudo de Sousa e Proença (2019) sobre a pouca participação dos alunos. Ao contrário disso, no estudo de Vargas e Noguti (2020), os alunos demonstraram interesse nas discussões e reflexões durante as aulas.
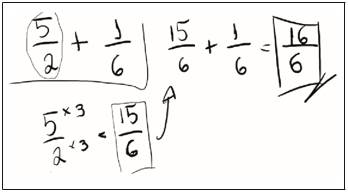
Por fim, na quinta ação, Articulação das estratégias dos alunos ao conteúdo, o foco foi utilizar uma das estratégias previstas, da ação de escolha do problema, para direcionar os alunos na articulação para o novo conteúdo, e do algoritmo da adição. Nesse momento, também foi possível mostrar a participação dos alunos. Nesta ação, uma vez que os alunos seguiram uma estratégia (tentar diretamente operar com as duas frações), cujas duas execuções foram equivocadas, o professor-pesquisador apresentou-lhes diretamente a forma do algoritmo da operação de adição de frações pelo cálculo do m.m.c. Mas, antes, tomamos como referência um exemplo para explicar como ocorre a equivalência de frações, baseado na estratégia de “uso da equivalência de frações”, devido a sua importância como conteúdo estrutural que permite operar com adição de frações sem recorrer ao algoritmo, conforme mostra a Figura 6 e o diálogo a seguir:
Professor: Os denominadores são iguais?
A7: Não.
Professor: Eu vou escolher uma fração para fazer a equivalência. Qual das duas frações aqui eu escolho: a cinco meio ou a um sobre seis?
A1: Cinco meio.
Professor: Beleza! Vou pegar o cinco meio. Qual meu objetivo fazendo a equivalência? É chegar ao denominador igual aqui ao 6! Trocar o 2 pelo 6! Então, que número vou multiplicar toda essa fração para que o dois seja igual a seis?
A7: 3.
Professor: E quanto é 2x3?
A7: É 6.
Professor: E agora o denominador seis aqui embaixo (
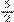 =
=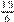 fração que estamos fazendo equivalência) é igual ao seis denominador aqui acima (a fração
fração que estamos fazendo equivalência) é igual ao seis denominador aqui acima (a fração 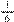 da adição de
da adição de 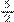 +
+ 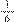 ), beleza? Vamos usar essa equivalência aquí. O que eu coloco aqui no lugar do cinco meio?
), beleza? Vamos usar essa equivalência aquí. O que eu coloco aqui no lugar do cinco meio?A7: Quinze sobre seis.
Professor: Então eu coloco quinze sobre seis mais o um sobre seis. Agora, vamos adicionar aquí. Embaixo eu vou adicionar?
A8: Não.
Professor: Então vai ficar seis aqui embaixo e acima eu vou adicionar?
A8: Sim, fica 16.
Professor: Então esse é o resultado da nossa adição de frações:
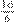 .
.
Após essa apresentação do cálculo da adição das duas frações pelo caminho da equivalência de frações, o professor-pesquisador passou a apresentar o algoritmo da operação de adição. A Figura 7 e o diálogo a seguir mostram como isso ocorreu.
Professor: Essa forma matemática que eu vou explicar para vocês chama-se mínimo múltiplo comum. Alguém já ouviu esse nome?
A2: Eu já ouvi m.m.c.
Professor: Alguém sabe como operar isso aqui?
A2: Não.
Professor: A gente usa m.m.c. para fazer adições e subtrações de frações que tem que achar um denominador igual, comum entre eles. Dessa adição
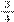 +
+ 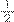 , alguém tem ideia de como a gente faz para achar os denominadores iguais sem usar a equivalência de frações?
, alguém tem ideia de como a gente faz para achar os denominadores iguais sem usar a equivalência de frações?A6: Não.
Professor: Vou explicar a vocês como fazer para achar o m.m.c. Eu gostaria que todos pegassem uma folha agora para escrever também comigo, tá bom? Vocês vão no cantinho da folha, escrevam aí os denominadores que a gente quer (4 e 2). A gente fará o denominador igual. Peguem os dois denominadores aqui e escrevam no cantinho “4, 2” e passem um traço aqui. Assim, para o 4 e 2, vamos utilizar os números que dividem o quatro ou o dois ao mesmo tempo. Vamos iniciar pelos menores números que dividem o 4 e o 2. Qual o primeiro número que eu posso utilizar para dividir o dois ou quatro?
A2: 2.
Professor: Então coloca o dois aqui. Quanto é 4 dividido por 2?
A2: 2.
Professor: Então desce o 2 aqui. E quanto é 2 dividido por 2?
A6: 1.
Professor: Então desce o número um aqui. Esse será o resultado? Não! A gente só acaba quando tiver o número um e um aqui embaixo, beleza? Vamos para essa linha aqui embaixo, agora. Tem algum número que eu consigo dividir por dois?
A2: 2.
Professor: Então, eu vou colocar aqui de novo o número 2 e daí 2 dividido por 2 será 1 para aqui embaixo. Aí acabou. O que a gente faz agora aqui? Multiplicamos os dois números 2 que apareceram aqui do lado do traço. Quanto é 2x2?
A2: 4.
Professor: Isso, é 4! Esse é o nosso m.m.c.! O valor do m.m.c. vai ser o nosso novo denominador. Vou colocar aqui embaixo para ficar mais fácil: esse 4 e esse 4. É o valor aqui que a gente achou. Agora, tem uma coisa, vocês vão ouvir muito na sua vida inteira que é: divide pelo debaixo e depois multiplica pelo de acima. Vocês vão pegar esse 4 que é o denominador e dividir pelo denominador de cada fração e depois multiplicar o respectivo resultado pelo numerador de cada fração. Ou seja, para cada fração, vocês vão pegar esse 4 aqui e dividir pelo de embaixo e depois pegar o resultado disso e multiplicar pelo de acima. Quanto é 4 dividido por 4?
A2: 1.
Professor: Quanto que é 1 x 3?
A2: 3.
Professor: Quanto que é 4 dividido por 2?
A6: 2.
Professor: Quanto que é 1x2?
A2: 2.
Professor: A adição das frações novas então ficou. Olha só os denominadores aqui, não são iguais?
A2: Sim.
Professor: Eu posso fazer essa adição aqui então. Quanto que vai dar aqui?
A2: Aqui embaixo vai ser 4.
A6: Acima, 5.
Professor: Portanto, a adição das duas frações da situação da corrida de bicicleta para achar o total percorrido resulta em
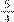 , ou seja, da forma como fizemos pelo m.m.c., será
, ou seja, da forma como fizemos pelo m.m.c., será 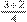 +
+ 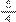 =
= 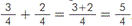 +
+ 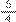 =
= 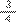 .
.
Tendo em vista essas apresentações (equivalência e o algoritmo da adição), o Quadro 5 a seguir mostra como se deu a participação dos alunos quando o professor-pesquisador apresentou essa forma matemática de resolução (novo conteúdo a ser estudado).
Quadro 5: Participação dos alunos na ação de articulação ao conteúdo
| Participação | Aluno(s) |
|---|---|
| Apenas assistiu às explicações | A3, A4, A5, A9 e A10 |
| Se manifestou, respondendo às perguntas durante a apresentação | A1, A2, A6, A7 e A8 |
Fonte: autores.
Verificamos no Quadro 5 que cinco alunos não se manifestaram pelo Google Meet durante as apresentações do professor-pesquisador, o que foi similar ao estudo de Sousa e Proença (2019) ao mostrarem que nas aulas presenciais, na ação de articulação da estratégia ao conteúdo de equação, os alunos de sete grupos foram poucos participativos. Já os outros cinco alunos participaram respondendo às perguntas durante as resoluções, o que foi similar ao estudo de Vargas e Noguti (2020), no qual os alunos mostraram interesse na sistematização do conteúdo de progressão aritmética. Apesar disso, em ambos os dois tipos de participação, identificamos alunos que apontaram compreender o algoritmo da operação da adição, conforme diálogo a seguir.
Professor: Vocês conseguiram entender?
A1: Sim.
A3: Eu pensei que era mais difícil.
A7: Eu consegui entender.
Enfim, a proposta de ensino se encerrou justamente com a apresentação/formalização do algoritmo da operação de adição de frações, a qual, segundo Proença (2018), foi feita porque não foi possível realizar uma articulação, porém, foi a postura prevista. Em continuidade da aula, propusemos três exercícios para que os alunos aplicassem o cálculo do m.m.c., seguindo o algoritmo estudado.
Considerações finais
A presente experiência de caso educativo teve como objetivo compreender a contribuição de um ensino da operação de adição de frações via resolução de problemas para a aprendizagem dos alunos. Para isso, foi elaborada uma proposta de ensino com resolução de problemas de acordo com as cinco ações do EAMARP de Proença (2018).
Os principais resultados sobre as dificuldades dos alunos nas etapas de resolução de problemas revelaram que a estratégia escolhida (planejamento) foi única e que a sua execução foi incorreta. Esperávamos que os alunos mobilizassem conhecimentos como uso de equivalência de frações, pois o enunciado já apontava as duas frações. Também era possível que fizessem uso de desenhos, o que envolveria a ideia de equivalência de frações. Dessa forma, quando se realiza o ensino na abordagem do EAMARP, pudemos revelar que os alunos não conseguiram fazer uso de estratégias de resolução, evidenciando suas dificuldades no uso de conhecimentos anteriores que deveriam estar bem formados.
Esse resultado mostra que esses alunos podem não estar sendo levados a aprender a resolver problemas e a aprender Matemática. Isso indica a necessidade de envolvê-los em aulas que revejam e rediscutam esses conhecimentos do ponto de vista conceitual e procedimental, pois a ideia de todo do conceito de fração e a de equivalência não foram utilizadas, de modo que possivelmente não estavam desenvolvidas para uso na resolução de problemas.
Sobre a participação dos alunos nas aulas, verificamos que houve envolvimento, sendo em maior grau na ação de auxílio aos alunos, diminuindo na ação de discussão das estratégias e tendo mais participação na ação de articulação. Nesse sentido, é possível apontar que o EAMARP proporcionou a participação ativa dos alunos e, de certa forma, motivou-lhes a se envolverem na aprendizagem, o que está na direção dos estudos de Vieira et al. (2013), Sousa e Proença (2019), Vargas e Noguti (2020) e Oliveira e Proença (2020) em que o trabalho feito em sala de aula com uso do problema como ponto de partida contribuiu positivamente para a aprendizagem dos alunos.
Contudo, podemos apontar que realizar o EAMARP contribuiu no sentido de que os alunos puderam vivenciar a resolução de problemas, podendo mobilizar seus conhecimentos, apesar da execução da estratégia não ter possibilitado encontrar uma solução correta ao problema. O favorecimento das aprendizagens dos alunos pode ser apontado em termos de que resgatamos um uso da equivalência de frações para tornar claro o erro que cometeram na forma como realizaram a adição das duas frações. Com isso, a articulação entre a estratégia de uso da equivalência e o novo conteúdo permitiu levar os alunos a entenderem o uso do algoritmo da adição de frações e como a fração equivalente aparece nesse procedimento matemático.
Como limitações do estudo, realizar as aulas na forma online dificultou estabelecer o trabalho em grupo e, assim, não houve as trocas de ideias entre os alunos, porém nada que os impossibilitassem de resolver o problema. Sobre as aulas realizadas, estudos que vierem a utilizar o EAMARP poderiam incentivar uso das estratégias previstas como sugerir que tentassem fazer desenhos ou sugerir a adequação de equivalência de frações, escolha essa que não adotamos em nosso ensino e estudo. Portanto, para implementações futuras de propostas de ensino que se direcionem ao estudo de conteúdos matemáticos, bem como o conteúdo de frações, sugerimos que as práticas pedagógicas se alicercem nas cinco ações do EAMARP e que possam realizar o trabalho em grupo, agora com as aulas presenciais retornando nas escolas, e revelar limites e possibilidades desse ensino e dos aprendizagens dos alunos.