PRODUCCIÓN FARMACÉUTICA

 

MÉTODO EXTENDIDO DE HILDEBRAND EN LA PREDICCIÓN DE LA SOLUBILIDAD DE NAPROXENO EN MEZCLAS COSOLVENTES ETANOL + AGUA

 

EXTENDED HILDEBRAND SOLUBILITY APPROACH FOR NAPROXEN SOLUBILITY ESTIMATION IN ETHANOL + WATER COSOLVENT MIXTURES

 

 

Diana M. ARAGON N.¹; Diana P. Pacheco A.¹; Millar A. RUIDIAZ M.¹; Alejandro D. SOSNIK.²; Fleming MARTINEZ R.¹*
¹ Grupo de Investigaciones Farmacéutico-Fisicoquímicas, Departamento de Farmacia, Facultad de Ciencias, Universidad Nacional de Colombia. A.A. 14490, Bogota D.C. Colombia.
² Departamento de Tecnología Farmacéutica, Universidad de Buenos Aires, Consejo Nacional de Investigaciones Científicas y Técnicas. Buenos Aires, Argentina.

 

 

---

RESUMEN

El naproxeno (NAP) es un antiinflamatorio no esteroidal de amplio uso en la actualidad; sin embargo sus propiedades fisicoquímicas aún no han sido totalmente estudiadas. En la presente investigación se aplica el Método Extendido de Solubilidad de Hildebrand (MESH), desarrollado por Martin et al al estudio de la solubilidad del NAP en mezclas binarias etanol + agua a 298,15 K ± 0,05 K. Se utilizan el volumen molar y el parámetro de solubilidad del NAP calculados por los métodos de Fedors y van Krevelen, respectivamente. Se encuentra una adecuada capacidad predictiva del MESH al utilizar un modelo polinómico regular de quinto orden para NAP, relacionando el parámetro de interacción W con el parámetro de solubilidad de las mezclas solventes. Sin embargo, las desviaciones obtenidas en la solubilidad estimada, respecto a los valores experimentales, fueron de magnitud semejante a las obtenidas al calcular esta propiedad directamente, utilizando una regresión empírica del logaritmo de la solubilidad experimental del fármaco en función del parámetro de solubilidad de las mezclas cosolventes.

Palabras clave: naproxeno, estimación de solubilidad, Método Extendido de Solubilidad de Hildebrand, mezclas cosolventes

---

ABSTRACT

Naproxen (NAP) is a widely used non-steroidal anti-inflammatory drug; however their physicochemical properties have not been thoroughly studied. In this work, Extended Hildebrand Solubility Approach (EHSA) developed by Martin et al was applied to evaluate the solubility of NAP in ethanol + water cosolvent mixtures at 298.15 K ± 0.05 K. Molar volume and solubility parameter values of NAP, were calculated according to Fedors and van Krevelen methods. A good predictive capacity of EHSA was found using regular polynomial models in fifth order for NAP, when the W interaction parameter is related to the solubility parameter of the cosolvent mixtures. Nevertheless, deviations on estimated solubility obtained respect to experimental solubility values had shown the same order compared with those obtained directly by logarithm empirical regression means of experimental solubilities as a function of cosolvent solubility parameters.

Keywords: naproxen, solubility estimation, Extended Hildebrand Solubility Approach, cosolvent mixtures

---

 

 

INTRODUCCIÓN

El naproxeno (NAP, Figura 1) es un fármaco analgésico y antiinflamatorio derivado del ácido propiónico, ampliamente utilizado en la terapéutica actual para el tratamiento sintomático de la artritis reumatoidea, y en general para todo proceso agudo o crónico relacionado con dolor e inflamación (1). En el mercado farmacéutico colombiano, el NAP se presenta en tabletas, cápsulas, polvo para suspensión, y además como suspensión lista para administración peroral. Así mismo, este fármaco se consigue en forma inyectable en ampollas de 500 mg/5 mL (2).

 

Figura 1. Estructura molecular del naproxeno.

 

Según reportes de la literatura, las formulaciones líquidas inyectables se caracterizan por suministrar una alta dosis de fármaco en un pequeño volumen de producto; por lo tanto, algunas propiedades fisicoquímicas, tales como la solubilidad y los volúmenes ocupados por los principios activos y los otros componentes en la solución, se tornan muy importantes para el diseñador farmacéutico, ya que el conocimiento de estas propiedades, así como el adecuado manejo, y de ser posible, la predicción de estos fenómenos, facilitan de manera sustancial el desarrollo de los medicamentos (3).

Por lo anteriormente expuesto, en esta investigación se presenta un estudio fisicoquímico sobre la predicción de la solubilidad del NAP a 298,
15 K ± 0,05 K en mezclas binarias formadas por etanol y agua. El estudio está basado en el Método Extendido de Solubilidad de Hildebrand (MESH), el cual fue desarrollado por el Profesor Alfred N. Martin y otros investigadores para su aplicación práctica en sistemas de interés farmacéutico (4-8). Para este fin se determinó la solubilidad del NAP en los solventes puros y en diferentes mezclas cosolventes. Además, con el fin de aplicar el MESH a este sistema binario, a partir de medidas de densidad y de cálculos teóricos basados en contribución de grupos, se calcularon las contribuciones volumétricas de los solutos y de las mezclas solventes a las soluciones saturadas; así mismo se utilizaron algunos datos de la literatura sobre las propiedades relativas a la fusión de estos fármacos. Esta investigación constituye una ampliación de lo presentado recientemente en la literatura sobre el estudio de la predicción de la solubilidad de este mismo fármaco en los sistemas propilenoglicol + agua (9) y propilenoglicol + etanol (10), y del acetaminofeno en estos mismos sistemas cosolventes (11,12), en adición a los trabajos del Profesor Martin et al desarrollados con otros fármacos (4-8).

 

ASPECTOS TEÓRICOS

La solubilidad ideal de un soluto sólido en un solvente líquido para obtener una solución líquida (13), se calcula adecuadamente mediante la expresión [1]:

en la cual ΔH_fus es la entalpía de fusión del soluto, R es la constante de los gases (1,987 cal mol^–1 K^–1), T_fus es la temperatura absoluta de fusión del soluto y T_fus es la temperatura absoluta de la solución. Por otro lado, la solubilidad real (X₂) se calcula adicionando el término de no-idealidad (log γ₂) a la expresión anterior (Ec. [1]) (10-12), para obtener la siguiente ecuación:

El término γ₂ es el coeficiente de actividad del soluto en la solución saturada y debe ser determinado experimentalmente para soluciones reales, en las cuales se presentan interacciones de diversa índole, tales como los enlaces de hidrógeno; sin embargo, se han desarrollado diferentes técnicas para hacer estimados razonables de este término. Un ejemplo específico de tales aproximaciones lo constituyen las denominadas soluciones regulares, introducidas por Hildebrand y Scatchard, en las cuales, a diferencia de las soluciones ideales, se permite un ligero cambio entálpico positivo, esto es, se requiere suministrar una pequeña cantidad de energía para que se conduzca el proceso de solución, mientras que el cambio entrópico es el correspondiente a una solución ideal. La solubilidad en las soluciones regulares (10, 13, 14) se obtiene a partir de:

donde V₂ es el volumen molar parcial del soluto (cm³ mol^-1), θ₁ es la fracción volumétrica del solvente en la solución saturada y δ₁ y δ₂ son los parámetros de solubilidad del solvente y del soluto, respectivamente. El parámetro de solubilidad se define como la raíz cuadrada de la densidad de energía cohesiva y se calcula como: , donde ΔH_v es la entalpía de vaporización y V_l es el volumen molar del líquido. En la literatura (8, 15) se encuentran disponibles los valores de parámetro de solubilidad para muchos solventes y también para algunos compuestos sólidos, entre ellos varios fármacos.

La mayoría de soluciones de interés farmacéutico se desvían notoriamente del comportamiento de las soluciones regulares (debido al tipo de interacciones presentes, en particular la formación de enlaces de hidrógeno, y además, a la diferencia entre los volúmenes molares de solutos y solventes). Así, a comienzos de los años 80 del siglo pasado, Martin et al plantearon el MESH, el cual ha resultado muy útil para estimar la solubilidad de varios fármacos en sistemas cosolventes binarios y ternarios (4-12). Si se introduce el término volumétrico-energético A, definido como , entonces la solubilidad real de un soluto en cualquier sistema solvente se puede calcular a partir de:

en la cual el término W es igual a 2Kδ₁δ₂, y en donde K es el parámetro de Walker, introducido inicialmente para el estudio de soluciones de polímeros (16). El factor W compensa las desviaciones respecto al comportamiento de soluciones regulares y se calcula a partir de datos experimentales como:

donde γ₂, como se indicó anteriormente, es el coeficiente de actividad del soluto en la solución y se calcula como el cociente .

Los valores obtenidos experimentalmente para el factor W pueden ser correlacionados mediante análisis de regresión, usando polinomios regulares de orden superior en función del parámetro de solubilidad de las mezclas solventes así:

Estos modelos polinómicos pueden ser utilizados para estimar la solubilidad por cálculo reverso (regresión en el cálculo, usando la ecuación obtenida a partir de los datos experimentales), resolviendo esta propiedad a partir del factor W obtenido de la regresión polinómica (Ec. [6]).

 

MATERIALES Y MÉTODOS

Materiales

Se utilizaron los siguientes materiales: naproxeno USP (17); etanol absoluto R.A. Merck (EtOH); agua destilada (W) conductividad < 2 µS cm^–1; tamiz molecular Merck (números 3 y 4); filtros Durapore^® 0,45 µm Millipore Corp.; material aforado de vidrio.

Preparación de las mezclas cosolventes

Se prepararon mezclas binarias EtOH + W en composiciones desde 0,00 hasta 100,00 % m/m de EtOH variando de 10,00 en 10,00 % m/m, por pesada, en una balanza digital de platillo externo Mettler Toledo PB302 de sensibilidad ± 0,01 g.

Determinación de la solubilidad

Se colocaron cantidades específicas de las diferentes mezclas EtOH + W y de los solventes puros en frascos de vidrio NP (No parenteral: Tipo IV) y en cada uno se adicionó un exceso de NAP, se taparon los frascos, se agitaron mecánicamente en un agitador Burell^® Modelo 75 durante una hora y se colocaron en un baño termostático Magni Whirl Blue M a 313,15 K ± 0,05 K con agitación manual esporádica durante al menos 72 horas. Posteriormente se ajustó la temperatura en 298,15 K ± 0,05 K dejando las muestras durante al menos 24 horas para permitir la precipitación del exceso de fármaco disuelto. Se tomaron muestras de las soluciones sobrenadantes, las cuales fueron filtradas para eliminar partículas sólidas no disueltas, determinando su densidad con un densímetro digital DMA 45 Anton Paar conectado a un termostato Magni Whirl Blue M a 298,15 K ± 0,05 K, siguiendo un procedimiento descrito previamente (18), para facilitar la interconversión de unidades másicas y volumétricas. Las muestras fueron diluidas gravimétricamente con alcohol USP (17) y analizadas por espectrofotometría UV en un equipo BioMate 3 Thermo Electron Corp. Todos los procedimientos indicados se realizaron al menos tres veces y los respectivos resultados fueron promediados.

Cálculo de las contribuciones volumétricas

Puesto que en las ecuaciones [3], [4] y [5] se requieren las contribuciones volumétricas de cada componente a la solución saturada, en este trabajo inicialmente se utilizó el volumen específico aparente del soluto (VEA₂) para calcular estas contribuciones. El valor de VEA₂ en cualquier solución (10) se puede calcular como:

en la cual m₂ y m₁ son las masas de soluto y solvente en la solución saturada, respectivamente, VE₁ es el volumen específico del solvente (calculado como el recíproco de la densidad) y ρ_soln es la densidad de la solución. El volumen molar aparente se calcula multiplicando VEA₂ por la masa molar del fármaco considerado.

 

RESULTADOS Y DISCUSIÓN

En la Tabla 1 se presenta la composición másica y volumétrica de las mezclas solventes EtOH + W junto con las respectivas densidades y parámetros de solubilidad a 298,15 K (19). La fracción volumétrica (φ) se halló simplemente como el cociente entre el volumen de EtOH y la suma de los volúmenes de EtOH y W suponiendo aditividad de volúmenes (20). El parámetro de solubilidad de las mezclas cosolventes (δ_mix) se calculó mediante aditividad en términos volumétricos de acuerdo a: , en la cual δ_i es el parámetro de solubilidad de cada componente, en este caso 13,0 cal^1/2 cm^-3/2 para el EtOH y 23,4 cal^1/2 cm^-3/2 para el W a 298,15 K (8).

 

Tabla 1. Composición de las mezclas disolventes, densidad de las mezclas, fracción volumétrica de EtOH en las mezclas y parámetros de solubilidad de la mezclas a 298,15 K.

 

En la Tabla 2 se aprecian algunas propiedades fisicoquímicas del fármaco en estudio, tomadas de la literatura (21-23), mientras que en la Tabla 3 se presenta la densidad de las soluciones saturadas de NAP, además la solubilidad del fármaco, expresada en % masa/volumen (g/100 mL) y en fracción molar; observándose que la solubilidad experimental varía de forma no lineal con la composición cosolvente (24). En la Figura 2 aparecen la solubilidad experimental y la solubilidad calculada usando el modelo de soluciones regulares (Ec. [3]) en función del parámetro de solubilidad de las mezclas disolventes.

A partir de los valores de densidad de las mezclas solventes (Tabla 1) y de las soluciones saturadas (Tabla 3), junto con la solubilidad en % p/v (Tabla 3), se calcularon las fracciones volumétricas del solvente (φ₁) y los volúmenes molares aparentes del soluto (V₂) en las soluciones saturadas, mediante la Ec. [7] y la masa molar del fármaco (Tabla 2). Estos valores también se presentan en la Tabla 3.

 

Tabla 2. Algunas propiedades físicas y químicas del NAP.

^(a) Tomado de Budavari et al (21).
^(b) Tomado de Perlovich et al (22).
^(c) Tomado de Betageri et al (23).
^(d) Determinado en alcohol USP (17).

 

Tabla 3. Densidad de las mezclas saturadas, solubilidad en % m/v y en fracción molar del NAP en las mezclas, volumen molar del NAP y fracción volumétrica del solvente en la solución saturada en las mezclas a 298,15 K.

 

Figura 2. Solubilidad experimental y solubilidad calculada según el modelo de soluciones regulares de Hildebrand del NAP en función del parámetro de solubilidad de las mezclas solventes a 298,15 K.

 

En la literatura para este tipo de tratamientos predictivos de la solubilidad, tradicionalmente se ha asumido como constante el valor del volumen molar del soluto en la solución (8, 16), valor que en el caso de solutos sólidos (a causa de la gran dificultad en su determinación experimental), en la mayoría de los casos es calculado por métodos de contribución de grupos, dentro de los cuales el más popular es el propuesto por Fedors (25). Sin embargo, como se aprecia en la Tabla 3, esta propiedad no es constante sino que depende de la composición del medio solvente debido a las diferentes clases de interacciones intermoleculares presentes en estas soluciones, aunque los valores son bastante desproporcionados en el caso de las mezclas polares y, por lo tanto, de muy baja solubilidad, en particular en el agua pura (valor negativo enorme: -2095,5 cm³ mol^-1). Debe aclararse, sin embargo, que los valores de V₂ obtenidos en las mezclas de composición hasta el 30 % de EtOH no son confiables debido a la cercanía entre los valores de densidad de la solución saturada y la mezcla cosolvente. Por lo tanto, en este trabajo se utilizó el valor calculado por el método de Fedors, esto es 166,7 cm³ mol^-1 (Tabla 4), cercano al valor experimental obtenido en EtOH puro. En segundo lugar, la fracción volumétrica del solvente en la solución saturada se calculó según la expresión:

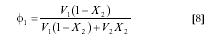
donde el término V₁ es el volumen molar del solvente. En el caso de la mezclas EtOH + W esta última propiedad se calculó mediante el método de aditividad lineal de volúmenes como: 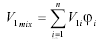Sin embargo, aunque es bien sabido que en el caso de mezclas cosolventes con fuerte presencia de enlaces de hidrógeno y grandes diferencias en los volúmenes molares de los componentes, los volúmenes de mezcla no son propiamente aditivos, este tratamiento ha sido ampliamente usado en este tipo de investigaciones (4-8).

 

Tabla 4. Aplicación de los métodos de Fedors y van Krevelen para la estimación del volumen molar y los parámetros de solubilidad parciales de Hansen y total de Hildebrand para el NAP.

^(a) Calculados de acuerdo a los valores presentados por Fedors (25).
^(b) Calculados de acuerdo a los valores y procedimientos descritos por Barton (26).
^(c) Parámetro parcial por fuerzas de dispersión.
^(d) Parámetro parcial por fuerzas dipolares.
^(e) Parámetro parcial por enlaces de hidrógeno.
^(f) Calculado restando al disustituido la diferencia existente entre el di y el monosustituido.
^(g) Parámetro de solubilidad total (1,0 cal1/2 cm-3/2 = 2,0455MPa1/2).

 

De otro lado, en la Tabla 5 se presentan los logaritmos de los coeficientes de actividad del fármaco en las diferentes mezclas, calculados utilizando la solubilidad ideal de 0,0833 para NAP a 298,15 K (22). En todos los casos, γ₂ es mayor que la unidad, debido a que la solubilidad experimental es menor que la ideal.

Adicionalmente, en la Tabla 5 pueden apreciarse los factores A, K y W. Para el cálculo del parámetro W se utilizó como valor del parámetro de solubilidad del fármaco, el obtenido mediante los métodos de Fedors (25) y de van Krevelen (26), esto es, 10,8 cal^1/2 cm^-3/2 (Tabla 4). Esto se hizo así ya que en este sistema no se obtiene el máximo de solubilidad en alguna mezcla cosolvente sino que este valor se obtiene en EtOH puro, a diferencia de lo encontrado en el caso de la solubilidad del acetaminofeno en otros sistemas cosolventes (11, 12).

 

Tabla 5. Logaritmo de coeficiente de actividad, factor A, factor K, factor W experimental y calculado utilizando modelos polinómicos regulares de órdenes 1, 2, 3, 4 y 5 a 298,15 K.

 

Como se indicó anteriormente, el factor W responde por las desviaciones presentadas por las soluciones reales respecto a las soluciones regulares, debido principalmente a interacciones específicas de tipo unión de hidrógeno, presentes en estos sistemas estudiados. El fármaco y los dos solventes considerados en este estudio pueden fácilmente establecer estas uniones, ya sea como donores o como aceptores de hidrógeno, debido a los grupos hidroxilo en los dos cosolventes, e hidroxilo, carbonilo y metoxilo en el fármaco (Figura 1).

En la Figura 3 se presenta la variación del factor W con el parámetro de solubilidad de las mezclas solventes, donde puede observarse un comportamiento que se desvía ligeramente de la linealidad. En la Tabla 5 se presentan los valores calculados o normalizados del factor W, obtenidos utilizando modelos de grados 1 a 5, donde es bien claro que estos valores dependen del tipo de modelo polinómico regular utilizado en la regresión. Situaciones similares han sido descritas por Martin et al (4, 8), al estudiar la cafeína en mezclas agua-dioxano, y por Martínez (11, 12), estudiando el acetaminofeno en mezclas propilenogicol + W y propilenoglicol + EtOH, al comparar los resultados obtenidos con polinomios de segundo y de cuarto orden.

 

Figura 3. Variación del factor W en función del parámetro de solubilidad de las mezclas solventes a 298,15 K.

 

En la Tabla 6 pueden observarse los valores de solubilidad calculados por cálculo reverso utilizando los diferentes valores del factor W obtenidos mediante las regresiones polinómicas de diferente orden que han sido presentados en la Tabla 5. Como criterio de comparación, se ofrecen en la Tabla 6 también los porcentajes de diferencia entre la solubilidad experimental y la calculada usando los diferentes modelos de regresión.

 

Tabla 6. Solubilidad calculada utilizando factor W obtenido por modelos de regresión de órdenes 1, 2, 3, 4 y 5, y porcentaje de diferencia respecto al valor experimental a 298,15 K.

 

Puede observarse que en la medida que se van haciendo más complejos los polinomios, se van obteniendo mejores concordancias entre los valores calculados y los experimentales, lo que se confirma al verificar los porcentajes de desviación promedio (3,8 % para orden 5). De manera similar a lo encontrado en otros estudios (4-12), en este caso el incremento más notable en la concordancia obtenida se presenta al pasar del orden 1 al 2, si bien en los siguientes pasos también se encuentran incrementos visibles, incluyendo el paso del orden 3 al 4, mientras que en el paso del orden 4 al 5, aparentemente no hay cambios significativos; sin embargo para los cálculos siguientes se utilizó el modelo con menor desviación general, esto es, el orden 5 (Ec. [9]).

Si bien la desviación general en la Ec. [9] es de 3,8 %, los valores más altos se encuentran en las mezclas cosolventes más polares, que contienen alrededor del 20% de EtOH, en las cuales aún puede presentarse agua voluminosa estructurada por enlaces de hidrógeno. Para verificar este posible efecto, en la Figura 4 se presenta el logaritmo decimal de la solubilidad en función de la polaridad de las mezclas. Así mismo se presenta la línea de solubilidad aditiva logarítmica según lo esperado de acuerdo al tratamiento de Yalkowsky y Valvani (27). Según esta figura se tiene que en las mezclas más polares la solubilidad es menor que la esperada según el modelo log-lineal y que en la mezcla cercana al 30 % de EtOH (19,7 cal^1/2 cm^-3/2) se pasa de desviaciones negativas a positivas.

 

Figura 4. Logaritmo decimal de la solubilidad experimental (----) y comportamiento aditivo logarítmico (------) de la solubilidad del NAP en función del parámetro de solubilidad de las mezclas solventes a 298,15 K.

 

Una explicación posible para las desviaciones negativas presentadas a bajas proporciones de cosolvente, podría hallarse en el trabajo de Kimura et al (28), quienes obtuvieron comportamientos similares en los calores de disolución de 1-metil-2-pirrolidinona en mezclas alcohol-agua, y según el cual, a bajas concentraciones de cosolvente, el agua retiene su habilidad para formar estructuras ordenadas.

Como es bien sabido, los cosolventes poseen grupos polares y no polares en su estructura molecular, y por lo tanto, se espera que la hidratación hidrofóbica ocurra alrededor de las partes no polares del compuesto (estructuración del agua formando agregados del tipo "témpano"), mientras que los enlaces de hidrógeno se forman entre los grupos polares y el agua. Aunque los alcoholes de pequeña masa molar generalmente han sido considerados como compuestos polares, Matsumoto et al (29) han ofrecido evidencia de la influencia del grupo metilo terminal de estos cosolventes sobre la estructuración del agua, mediante el estudio de las entalpías molares de exceso. Estas interacciones existentes entre los alcoholes y el agua podrían reducir la interacción entre el agua y el NAP, llevando a una solubilidad inferior a la esperada según la línea de aditividad.

En cambio, a altas concentraciones de cosolvente en las mezclas, la estructura tridimensional del agua se pierde y, por lo tanto, las moléculas de agua estarían más disponibles para interactuar con las moléculas del fármaco, lo cual, a su vez, llevaría a obtener solubilidades relativamente altas. Otra explicación plausible para las altas desviaciones encontradas estaría dada en función de un posible fenómeno de autoasociación del fármaco en la solución saturada (30); sin embargo, para verificar esto en el presente caso se requeriría de otro tipo de evidencia experimental, tal como el estudio de los coeficientes de distribución del NAP en función de la concentración, en diferentes sistemas solvente orgánico/agua.

En la literatura se ha presentado evidencia de tipo termodinámico para explicar el comportamiento de este sistema, en términos del cambio de conducción para el proceso de solución del fármaco, al pasar de una conducción entrópica por debajo del 30 % de EtOH a una conducción entálpica en concentraciones mayores del cosolvente (24). Se han explicado estos resultados como una consecuencia de la pérdida de estructura del agua presente alrededor de los grupos no polares del fármaco (dos grupos metilo y un naftilo, Figura 1), la cual se encontraba inicialmente asociada entre sí por hidratación hidrofóbica. Esta desestructuración se va produciendo en la medida que se reemplaza el agua por etanol.

Una reflexión que podría surgir respecto a la concordancia obtenida al comparar la solubilidad experimental con la calculada a partir de modelos de regresión construidos sobre datos experimentales directos o procesados, es la relativa a la justificación de cálculos complejos involucrando otras variables del sistema (Ec. [4] y Tablas 5 y 6), en lugar de la simple regresión de solubilidad en función del parámetro de solubilidad de la mezcla solvente (Tabla 3 y Figuras 2 y 4). Por lo tanto, en la Tabla 7 se comparan las solubilidades experimentales, las calculadas directamente como logaritmo decimal de X₂ mediante regresión polinómica regular de cuarto grado (Figura 4, Ec. [10]), y las calculadas indirectamente involucrando los parámetros W obtenidos del polinomio de quinto grado (Tabla 6, Ec. [9]). Así mismo, se presentan en esta tabla los respectivos porcentajes de diferencia, con respecto al valor experimental.

 

Tabla 7. Comparación de los valores de solubilidad calculados directamente y mediante el método extendido de Hildebrand.

 

En la Tabla 7 puede observarse que aparentemente no hay diferencias significativas entre los valores calculados por los dos métodos, lo que se verifica mediante los promedios de desviación, para los cálculos directo (4,9%) y por el Método Extendido de Hildebrand (3,8%), respectivamente. A diferencia de lo encontrado en el estudio del acetaminofén (10, 11), en el caso de NAP los resultados previos estarían demostrando una escasa practicidad del MESH, método que a su vez implica experimentación adicional (entre la que se destaca la determinación de densidades y de algunas propiedades relativas a la fusión del soluto). Sin embargo, debe tenerse presente que este método considera la solubilidad desde un enfoque fisicoquímico sistemático muy racional, y además porque únicamente haría falta encontrar un método efectivo para calcular el parámetro K de Walker, con el cual se calcularía el término W según la expresión 2Kδ₁δ₂ mencionada anteriormente, ya que los términos δ₁ y δ₂ serían conocidos, con lo que podría calcularse directamente la solubilidad del fármaco en cualquier composición cosolvente.

 

CONCLUSIONES

De lo descrito anteriormente se verifica que en este sistema solvente no se obtiene la máxima solubilidad de NAP en alguna mezcla cosolvente, por lo que el parámetro de solubilidad de este fármaco es inferior al correspondiente al solvente menos polar, esto es, el EtOH. La solubilidad experimental del fármaco en mezclas con menos del 80% de EtOH es menor que la respectiva solubilidad ideal, lo que a su vez conduce a coeficientes de actividad mayores que la unidad. Adicionalmente, en esta investigación se ha utilizado satisfactoriamente el MESH en el estudio de la solubilidad de NAP en mezclas EtOH + W, utilizando para este fin el volumen molar y el parámetro de solubilidad calculados por contribución de grupos. En particular, se ha encontrado una buena capacidad predictiva utilizando un modelo polinómico de quinto orden, del parámetro de interacción W en función del parámetro de solubilidad de las mezclas solventes. Sin embargo, al comparar los resultados obtenidos directamente y aquellos obtenidos con el MESH, se encuentra que en apariencia no hay mejoría significativa en el carácter predictivo al pasar desde el método estrictamente empírico hasta el método propuesto por Martin et al, a diferencia de lo encontrado en el estudio de otros fármacos.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Roberts II LJ, Morrow JD. Analgesic-antipiretic and anti-inflammatory agents and drugs employed in the treatment of gout. En: Hardman JG, Limbird LE, Gilman AG, editores. Goodman & Gilman's. The pharmacological basis of therapeutics. 10 ed. New York: McGraw-Hill; 2001. pp. 703-705.        [ Links ]

2. Rosenstein-Ster E. Diccionario de especialidades farmacéuticas. 31 ed. Bogotá: Thompson P.L.M., S.A.; 2003.        [ Links ]

3. Jiménez F, Martínez F. Una estrategia para la selección sistemática de vehículos en el diseño de formas farmacéuticas líquidas homogéneas. Rev Colomb Cienc Quím Farm 1995; 24(1): 19-23.        [ Links ]

4. Martin A, Newburger J, Adjei A. Extended Hildebrand approach: solubility of caffeine in dioxane-water mixtures. J Pharm Sci 1980; 69(6): 659-661.        [ Links ]

5. Martin A, Wu PL. Extended Hildebrand solubility approach: p-Hydroxibenzoic acid in mixtures of dioxane and water. J Pharm Sci 1981; 72(6): 587-592.        [ Links ]

6. Martin A, Miralles MJ. Extended Hildebrand solubility approach: Solubility of tolbutamide, acetohexamide, and sulfisomidine in binary solvent mixtures. J Pharm Sci 1982; 71(4): 439-442.        [ Links ]

7. Martin A, Wu PL, Adjei A, Mehdizadeh M, James KC, Metzler C. Extended Hildebrand solubility approach: testosterone and testosterone propionate in binary solvents. J Pharm Sci 1982; 71(12): 1334-1340.        [ Links ]

8. Sinko PJ. Martin's physical pharmacy and pharmaceutical sciences. 5 ed. Philadelphia: Lippincott Williams & Wilkins; 2006. pp. 247-250.        [ Links ]

9. Manrique YJ, Pacheco DP, Martínez F. Estimación de la solubilidad de ibuprofeno y naproxeno en mezclas propilenoglicol + agua, Póster presentado en: XVII Congreso Farmacéutico Argentino, Villa Carlos Paz, Córdoba, Argentina, 2006.        [ Links ]

10. Pacheco DP, Manrique YJ, Vargas EF, Barbosa HJ, Martínez F. Validez del método extendido de Hildebrand en la predicción de las solubilidades de ibuprofén y naproxén en mezclas propilenoglicol-etanol. Rev Colomb Quím 2007; 36(1): 55-72.        [ Links ]

11. Martínez F. Utilidad del método extendido de Hildebrand en el estudio de la solubilidad del acetaminofén en mezclas agua-propilenoglicol. Rev Acad Colomb Cienc 2005; 29(112): 429-438.        [ Links ]

12. Martínez F. Aplicación del método extendido de Hildebrand al estudio de la solubilidad del acetaminofén en mezclas etanol-propilenoglicol. Acta Farm Bonaerense 2005; 24(2): 215-224.        [ Links ]

13. Ávila CM, Martínez F. Thermodynamic study of the solubility of benzocaine in some organic and aqueous solvents. J Solution Chem 2002; 31(12): 975-985.        [ Links ]

14. Hildebrand JH, Prausnitz JM, Scott RL. Regular and Related Solutions. New York: Van Nostrand Reinhold; 1970.        [ Links ]

15. Hansen CM, Beerbower A. Solubility parameters. En: Kirk & Othmer: Encyclopedia of chemical technology, Suppl. 2 ed. New York: John Wiley & Sons; 1971. pp. 889-910.        [ Links ]

16. Martin A, Bustamante P. El parámetro de solubilidad en las ciencias farmacéuticas. Anal Real Acad Farm 1989; 55(2): 175-202.        [ Links ]

17. US Pharmacopeia 23 ed. United States Pharmacopeial Convention, Rockville, MD. 1994.        [ Links ]

18. Martínez F, Gómez A, Ávila CM. Volúmenes molales parciales de transferencia de algunas sulfonamidas desde el agua hasta la mezcla agua-etanol (X = 0.5). Acta Farm Bonaerense 2002; 21(2): 107-118.        [ Links ]

19. Jiménez J, Manrique J, Martínez F. Effect of temperature on some volumetric properties for ethanol + water mixtures. Rev Colomb Cienc Quím Farm 2004; 33(2): 145-155.        [ Links ]

20. Connors KA. Thermodynamics of pharmaceutical systems: an introduction for students of pharmacy. Hoboken, NJ: Wiley-Interscience; 2002. pp. 61-66.        [ Links ]

21. Budavari S, O'Neil MJ, Smith A, Heckelman PE, Obenchain Jr. JR, Gallipeau JAR, D'Arecea MA. The Merck index, an encyclopedia of chemicals, drugs, and biologicals. 13 ed. Whitehouse Station (NJ): Merck; 2001. p. 1149.         [ Links ]

22. Perlovich GL, Kurkov SV, Kinchin AN, Bauer-Brandl A. Thermodynamics of solutions III: Comparison of the solvation of (+)-naproxen with other NSAIDs. Eur J Pharm Biopharm 2004; 57(2): 411-420.        [ Links ]

23. Betageri GV, Nayernama A, Habib MJ. Thermodynamics of partitioning of nonsteroidal anti-inflammatory drugs in the n-octanol/buffer and liposome systems. Int J Pharm Adv 1996; 1(3): 310-319.        [ Links ]

24. Pacheco DP, Martínez F. Thermodynamic analysis of the solubility of naproxen in ethanol + water cosolvent mixtures. Phys Chem Liquids 2007; 45(5): 581-595.        [ Links ]

25. Fedors RF. A method for estimating both the solubility parameters and molar volumes of liquids. Polym Eng Sci 1974; 14(2): 147-154.        [ Links ]

26. Barton A. Handbook of solubility parameters and other cohesion parameters. 2 ed. New York: CRC Press; 1991. pp. 157-193.        [ Links ]

27. Yalkowsky SH. Solubility and solubilization in aqueous media. New York: American Chemical Society and Oxford University Press; 1999. pp. 180-235.        [ Links ]

28. Kimura F, Murakami S, Fujishiro R. Thermodynamics of aqueous solutions of nonelectrolytes. II. Enthalpies of transfer of 1-methyl-2-pyrrolidinone from water to many aqueous alcohols. J Solution Chem 1975; 4(3): 241-247.        [ Links ]

29. Matsumoto Y, Touhara H, Nakanishi K, Watanabe N. Molar excess enthalpies for water + ethanediol, + 1,2-propanediol, and + 1,3-propanediol at 298.15 K. J Chem Thermodyn 1977; 9(8): 801-805.        [ Links ]

30. Rubino JT, Obeng EK. Influence of solute structure on deviations from the log-linear solubility equation in propylene glycol: water mixtures. J Pharm Sci 1991; 80(5): 479-483.        [ Links ]

 

AGRADECIMIENTOS

Agradecemos muy formalmente a la DIB-DINAIN de la Universidad Nacional de Colombia (UNC) por el apoyo financiero y al Departamento de Farmacia de la UNC por facilitar los equipos e instalaciones requeridos para el desarrollo de esta investigación.

 

 

Recibido: Octubre 19 de 2007; Aceptado: Abril 8 de 2008

 

 

* Autor a quien se debe dirigir la correspondencia: fmartinezr@unal.edu.co