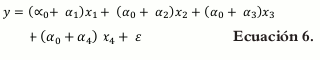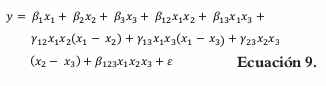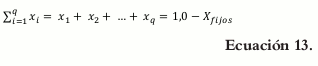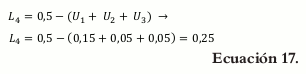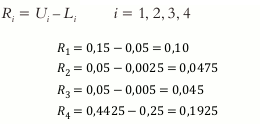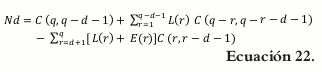INDUSTRIAL FARMACÉUTICA

El objetivo principal de este trabajo es aplicar el diseño experimental de mezclas a la formulación de una forma farmacéutica sólida (ibuprofeno) mediante el estudio de sus excipientes y la proporción de éstos en la formulación, además de mostrar cómo el personal de investigación y desarrollo en las empresas farmacéuticas nacionales puede utilizar las herramientas estadísticas, como el diseño experimental de mezclas, para obtener un producto con las características requeridas, y posteriormente su optimización reduciendo no sólo los costos de investigación sino también los costos de producción. El diseño experimental de mezclas permite estudiar el comportamiento de la formulación de ibuprofeno desde el punto de vista farmacotécnico, a través del análisis del ángulo de reposo, la dureza del núcleo y la friabilidad, además del índice de Carr's caracterizando una superficie de respuesta que permite un eficiente aprovechamiento de esta metodología para la resolución del problema de formulación. El ángulo de reposo muestra que se debe mejorar la fluidez de la formulación para garantizar un correcto llenado de las matrices en el proceso de tableteado a escala industrial, los parámetros de dureza y friabilidad muestran que las formulaciones cumplen y que se puede seguir con un proceso de optimización de la formulación.

Palabras clave: diseño experimental de mezclas, investigación y desarrollo, superficie de respuesta.

The principal aim of this paper is to apply the experimental design of mixtures to formulate a solid dosage form (ibuprofen) through the study of the excipients and their proportion in the formulation. Besides it shows to the research and development teams in the pharmaceutical national companies how they can use statistical tools like the experimental design of mixtures to obtain a product with the required characteristics. The optimization of this one reduces not only the costs of investigation but also the costs of production. The experimental design of mixtures allows to typify the performance of the ibuprofeno formulation from the pharmatechnic point of view, as well as the angle of rest, hardness of the nucleus and friability. Besides Carr's's index, characterizing a surface of response that allows an efficient utilization of this methodology for the resolution of the problem of formulation. The angle of rest shows that it is necessary to improve the fluency of the formulation to guarantee a correct filling of the counterfoils in the rattling process on an industrial scale. The parameters of hardness and friability show that the formulations are correct and that it is possible to continue with a process to optimize the formulation.

Key words: experimental design of mixtures, research and development, surface of response.

En los últimos años la industria farmacéutica se ha dado a la búsqueda de procedimientos que optimicen la velocidad de respuesta, reduciendo los tiempos de fabricación y los costos asociados a la manufactura de un producto sin que necesariamente esto afecte su calidad. El sector farmacéutico no es ajeno, a la tendencia de simplificar sus procesos en áreas críticas como la fabricación de formas farmacéuticas sólidas.

Las tabletas, los preparados farmacéuticos más comúnmente utilizados, disponibles en varias formas y administración por vía oral, han llegado a ser la elección habitual tanto de la industria farmacéutica como de los pacientes, gracias a múltiples ventajas como su bajo costo de manufactura, la facilidad en su almacenamiento, dispensación y administración; además, su gran versatilidad en la liberación del principio activo, que puede ser controlada al modificar el diseño y el contenido de la formulación farmacéutica. Excipientes tales como diluyentes, aglutinantes y lubricantes, generalmente son necesarios en la formulación para facilitar el proceso de manufactura y brindar propiedades mecánicas adecuadas en el comprimido. En este punto es importante la elección de los excipientes adecuados para optimizar el desarrollo de una formulación deseada (1).

Es importante destacar la necesidad de explorar técnicas de diseño y formulación para los principios activos que permitan reducir tiempo y costo de manera eficiente y que, a su vez, permitan que las propiedades farmacotécnicas garanticen un comprimido de excelente calidad. Dentro de las metodologías se encuentra el diseño experimental de mezclas (2), estrategia que permite evaluar de manera consistente la influencia de cada uno de los componentes de una formulación, en este caso los excipientes, y el papel que desempeñan en el proceso de manufactura de una tableta por compresión directa. El diseño experimental de mezclas ha sido utilizado para la compresión de tabletas con pobres características de compactación (3), también en la mejora de la solubilidad de principios activos (4), en la obtención de mezclas que permitan la extracción óptima de metabolitos secundarios en plantas de interés farmacéutico (5). Así, el diseño de mezclas ha llegado a ser una metodología adecuada para asumir el diseño y la pre-formulación, permitiendo identificar comportamientos en las variables que pueden afectar el proceso de manufactura a nivel industrial y que pueden ser corregidas desde el proceso de formulación.

Diseño experimental con mezclas

Las formulaciones farmacéuticas son casi todas, invariablemente, mezclas de excipientes y principio activo. En este caso la respuesta experimental puede ser una propiedad de la mezcla, y el factor mezcla, definido como la composición de la misma (6). En este caso es importante distinguir entre la proporción de ingredientes en una formulación y el total de la formulación; donde una mezcla es definida por la proporción de sus componentes y no por la cantidad de la mezcla (7).

En un experimento de mezclas, si la cantidad total de la mezcla se mantiene constante y el valor de la respuesta cambia cuando se modifica la proporción relativa de los ingredientes que la componen, el comportamiento de la respuesta es definido como una función conjunta característica de los ingredientes en la mezcla (8).

Tanto el principio activo (ibuprofeno) como los excipientes (avicel, estearato de magnesio, PVP y lactosa) fueron facilitados por la planta de producción de medicamentos de la Universidad de Antioquia, las cuales fueron adquiridas por ésta en Representaciones DIVER Ltda.

Equipos

Para el proceso de tableteado se utilizó una tableteadora Stokes B2; la dureza se midió en un durómetro marca Vankel modelo VK 200 (strog-cobb); y la friabilidad se midió en un friabilizador Vankel modelo 45-2000. El software estadístico utilizado es el Design-Expert® versión 7.0.0, Stat-Ease, Inc.

Se midieron el ángulo de reposo para la mezcla de polvos, la dureza y la friabilidad para las tabletas como variables respuesta, además se estimó el índice de Carr's para determinar la densidad aparente de la mezcla.

Diseño experimental de mezclas

Para el experimento de mezclas se aplicó un diseño no simple con restricciones (8) (Véase figura 1), donde la forma del dominio experimental no se caracteriza por un triángulo o pirámide, sino por un poliedro, de acuerdo a las restricciones que toma cada componente (Véase figura 2).

Figura 1. Arreglo dimensional para una mezcla de 4 componentes.

Figura 2. Región experimental restringida según el sistema de 4 componentes, dada por las restricciones en la proporción de los componentes 0,05 < x₁ < 0,15 - 0,0025 < x₂ < 0,15 - 0,005 < x₃ < 0,05 - 0,25 <x₄ < 0,4425

La cantidad de ibuprofeno se fijó en 300 mg, y la cantidad de excipientes, en 300 mg (X₁ + X₂ + X₃ + X₄ = 100%, = ∑_x=1ⁿ 1,0) para un peso total de la tableta de 600 mg. Para los X_i (véase la tabla 1).

Siguiendo el modelo experimental el arreglo para cada variable es el siguiente:

Donde q representa el número de componentes (o constituyentes) en el sistema bajo estudio, y x representa la proporción del i-ésimo constituyente en la mezcla. La sumatoria de la proporción de los componentes o su fracción debe ser igual a la unidad.

La proporción de cada excipiente en cada formulación tiene ciertas restricciones que se traducen en el hecho de que cada componente x_i de la mezcla se encuentra entre unos límites que no van desde 0,0 hasta 1,0 (8). A este tipo de restricción en los constituyentes se le conoce como pseudocomponente y está representado de la siguiente forma para el componente i.

Donde L_i (L-pseudocomponente) es la restricción inferior, y U_i (U-pseudocomponente) representa la restricción superior.

Modelo matemático para caracterizar la superficie de respuesta en la región experimental

Ecuación canónica de primer orden.

El modelo matemático para la ecuación de primer orden es el siguiente:

Debido a que la suma de todos los componentes es la unidad ∑_x=1ⁿ 1,0 se puede remplazar α₀ por α₀(x₁ + x₂ + x₃ + x₄) (7).

ó

Donde β_i = α₀ + α_i

La ecuación de primer orden permite caracte­rizar cómo cada factor influye de manera inde­pendiente en la respuesta. Para todas las ecuaciones, ε es un componente del error aleatorio que tiene distribución normal con media cero y varianza σ².

Ecuación canónica de segundo orden o ecuación cuadrática

El modelo matemático para la ecuación de segundo orden es:

La ecuación de segundo orden permite identificar las posibles interacciones en mezclas binarias entre dos de los componentes de la mezcla total.

Ecuación canónica de tercer orden (modelo cúbico y modelo cúbico reducido)

Si el modelo de segundo orden no es adecuado, o no presenta un buen ajuste, es necesario un modelo de orden mayor, generalmente de tercer grado. La expresión canónica completa para la mezcla de tres componentes es conocida como modelo cúbico y se escribe de la siguiente forma:

El modelo cúbico reducido omite los términos γ_ijx_ix_j(x_i - x_j) (6) (7), que representan las interacciones cúbicas de dos componentes.

Puesto que las variables para el diseño experimental son 4 (lubricante, desintegrante, compactante y diluyente) el modelo completo es el siguiente:

Estos modelos son conocidos como modelos Scheffé (7).

De acuerdo con el modelo a caracterizar en la respuesta de superficie, el número mínimo de experimentos debe ser igual al número de términos con los que cuente el modelo.

Construcción del diseño experimental

La tabla 1 muestra la función que cumplen los excipientes en la formulación y los niveles mínimos y máximos.

Tabla 1. Dominio experimental inicial para la formulación de Ibuprofeno tabletas.

Debido que el diseño experimental cuenta con valores fijos, como son el principio activo (ibuprofeno) o algún otro ingrediente (Véase tabla 1), los arreglos para cada variable cambian.

Donde x'_i representa el i-ésimo componente en la mezcla en términos de pseudocomponentes y q representa los componentes de la mezcla.

Puesto que el principio activo fue fijado, la suma de la proporción de las variables debe ser igual a la unidad restándole los valores de las variables fijadas.

En términos de los pseudocomponentes, y de acuerdo con la restricción asignada a los valores fijos, la proporción de los componentes queda representada así:

En este caso las restricciones para los componentes quedan representadas de la siguiente forma:

Debido a que la lactosa (X₄) no tiene definidas sus restricciones, éstas deben ser calculadas para detectar si hay alguna inconsistencia.

Calculando L₄:

Calculando U₄:

De acuerdo con esto las restricciones quedan representadas de la siguiente manera:

Para la detección de inconsistencias en las restricciones, la resolución completa de la detección de las restricciones y el cálculo de los límites dimensionales, remitirse a (8).

Calcular el rango R_i para cada x_i

Calcular el rango R_L para L-pseudocomponente y el rango R_U para U-pseudocomponente

Debido a que ningun R_i > R_L ∀ = 1,2,3,4, y ningún R_i > R_U ∀ = 1,2,3,4, las restricciones no presentan indonsistencias.

Cálculo del número de límites d-dimensionales (vértices, bordes y caras del poliedro) en la región de restricción

La siguiente fórmula (9) es utilizada para calcular el número de límites d-dimensionales (d= 0,1,...,4-2), donde d representa los límites dimensionales de una región definida de acuerdo con restricciones consistentes

El primer paso es calcular el rango R_i = U_i - L_i, i= 1,2,3 y 4, para cada uno de los componentes y calcular R_L = 1 - ∑_i=1^q L_i y R_U = ∑_i=1^q U_i - 1. Ahora, R_p, es el valor mínimo entre R_L y R_U.

El número de combinaciones de q se extiende r veces de acuerdo a C_(q,r)= q!/r!(q-r)!, donde q representa los componentes de la mezcla y r las posibles combinaciones que existen entre ellos.

C_{(q, r)} se divide en tres componentes mutuamente excluyentes para r = 1, 2,..., q.

L_(r) = Número de combinaciones de los componentes cuyos rangos suman un número menor que R_p

E_(r) = Número de combinaciones de los componentes cuyos rangos suman un número igual a R_p

G_(r) = Número de combinaciones de los componentes cuyos rangos suman un número mayor que R_p.

Se tiene que:

De acuerdo con esto, la fórmula para calcular el número de límites d-dimensionales de la región definida es:

donde d = 1,2,...,q-2 y d representa las dimensiones por construir, si d=0 se determinan los vértices, para d=1 se determinan los lados y para d=2 se determinan las caras del poliedro.

La ecuación para los vértices, d=0

Para d = 1

Se tiene que

Ahora R_p = mín. (R_L, R_U), R_p= mín. (0,1925 y 0,1925), entonces R_p = 0,1925.

Se tiene que r es igual al número de combinaciones entre los componentes, entonces r= 1,2,3 y 4.

Calculamos L_(r), E_(r), G_(r)

Cuando:

Se tiene que:

De acuerdo con esto, el arreglo reemplazando en la ecuación 22 para los vértices, lados y caras del poliedro es el siguiente

Vértices = 8 Lados = 12 Caras = 6

Cálculo de las coordenadas para los vértices en la región de restricción

Existen varios algoritmos para el cálculo de las coordenadas de los vértices, entre ellos el algoritmo de los vértices extremos, de McLean y Anderson (9); el algoritmo de XVERT, de Snee y Marquardt (9); y el algoritmo XVERT1, de Nigam, Gupta y Gupta (9). Este último no calcula todos los vértices de la región de restricción. Los dos últimos son similares al algoritmo de los vértices extremos, de McLean y Anderson (9), por tal razón este se utilizará para el cálculo de las coordenadas de los vértices del poliedro.

Algoritmo de los vértices extremos de McLean y Anderson

Este algoritmo es utilizado para la determinación de aquellos vértices que están definidos como la combinación de los límites superiores e inferiores de las restricciones, y puede ser obtenido directamente de la utilización de los límites superior e inferior de q-1 componentes (9).

Ahora se procede a llenar los espacios en blanco (Véase tabla 2), observando siempre que el valor que va en ese espacio esté dentro de las restricciones para cada factor, el espacio en blanco se determina así:

Tabla 2. Listado de todas las posibles combinaciones de los 4 componentes de la mezcla para una formulación de ibuprofeno tabletas, según el algoritmo de McLean y Anderson.

De acuerdo con esto, los puntos 1, 2, 3, 4, 5, 6, 7 y 8 (Véase tabla 3) son los vértices extremos que cumplen con las restricciones para cada componente; los puntos 10, 15, 18, 23, 26 y 31 son repeticiones en los primeros 8 puntos y, por lo tanto, se descartan.

Tabla 3. Coordenadas de los vértices del poliedro según el algoritmo de McLean y Anderson.

Determinación del número de experimentos por realizar

Con respecto al modelo matemático a utilizar es el número de experimentos a desarrollar. Para el modelo de segundo orden se necesitan (ecuación 26) distintos puntos que representan los coeficientes dentro de la ecuación canónica.

Siempre que se va a determinar una superficie de respuesta para un diseño experimental de mezclas se parte de la ecuación canónica de segundo orden; por lo tanto, se aplica la ecuación 26 para determinar el número de experimentos mínimos a realizar.

El número mínimo de experimentos a realizar es 10. Es importante anotar que con sólo diez experimentos se sacrifica bastante precisión en los parámetros estimados en términos de sus varianzas, como también la precisión en el predictor (9). Así pues, es importante asegurar la precisión, tanto de los parámetros a estimar como del predictor, adicionando tantos puntos como sea posible. La mejor manera es que cada vértice represente un experimento, además de que se adicione un experimento por cada cara del poliedro y un experimento representado por el centro del poliedro (9), los experimentos en las caras y en el centro del poliedro permiten determinar si la superficie de respuesta es no lineal. De acuerdo con esto, para la formulación de ibuprofeno tabletas serían en total 8 experimentos por cada una de las caras y un experimento que represente el centro del poliedro, para un total de 15 formulaciones a ensayar (Véase figura 3). Los centros de las caras se calculan dejando un factor fijo, ya sea en su restricción inferior o superior, y tomando el valor medio entre la restricción superior e inferior de los componentes restantes. El centro del poliedro se calcula tomando el valor medio entre las restricciones inferiores y superiores de todos los componentes

Figura 3. Vértices y centroides del poliedro en la región de restricción. Los números indican el punto del diseño.

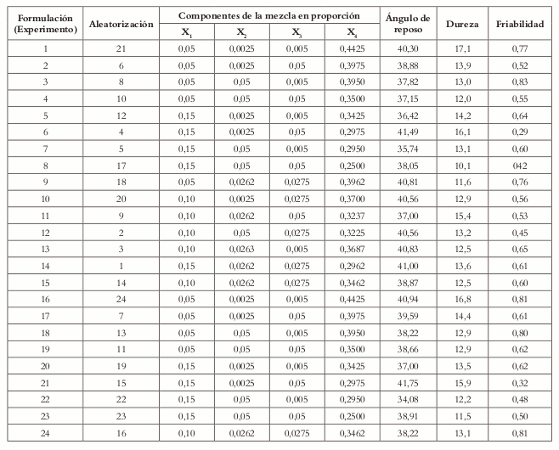
De acuerdo con el diseño experimental de mezclas, el número total de experimentos fue de 15, que representan los ocho vértices del poliedro, los 6 centroides de las caras, y el punto central del poliedro, que constituye el punto medio de la mezcla. Para garantizar la precisión se replicaron puntos en el diseño experimental. Los puntos replicados fueron los vértices y el centro del poliedro para un total de 24 experimentos (Véase tabla 4). Los resultados del diseño completo se encuentran resumidos en la tabla 5 donde, además, aparecen las formulaciones aleatorizadas en el orden de corrida para disminuir el sesgo por fatiga de los equipos de medición y compresión.

Tabla 4. Arreglo experimental.

Tabla 5. Resultados y aleatorización de los experimentos.

Ángulo de reposo

Los resultados obtenidos para el ángulo de reposo muestran que todas las formulaciones presentan un flujo pobre, pero esto no indica necesariamente que las mezclas no sean adecuadas, de hecho, estas mostraron que tenían capacidad para fluir de manera libre, pero en estado estático las formulaciones presentaban alta cohesión, propiedad que indica la capacidad que tienen los excipientes de permanecer juntos, característica dada por el compactante, lo cual se vio reflejado den el índice de Carr's, donde valores muy altos indican la poca capacidad de las mezclas para fluir por si solas, es decir, necesitan estar en movimiento para generar flujo constante (Véase tabla 66).

Tabla 6. Pesos promedios e Índice de Carr's.

El ángulo de reposo es una propiedad característica, que indica cómo se comportará la mezcla en el proceso de tableteado permitiendo el llenado de la matriz para su posterior compresión, y que se ve reflejado en el peso promedio de la tableta. En la tabla 6 se encuentra resumido el valor del peso promedio e índice de Carr's de las formulaciones donde puede observarse una alta variabilidad en los pesos de las tabletas

Según la suma de cuadrados tipo I (Véase tabla 7), los modelos canónicos cuadrático y cúbico especial representan mejor la respuesta de superficie y los factores, el modelo cúbico completo presenta problemas de confusión. Para determinar cual modelo ese el más adecuado, se procede a verificar la falta de ajusta para todos los modelos

Tabla 7. Suma de cuadrados tipo I para el modelo secuencial.

Prueba de falta de ajuste

La prueba de falta de ajuste indica que el modelo cuadrático presenta problema en su ajuste con un valor p (0,0005) significativo para el modelo

El modelo cúbico especial tambien muestra una falta de ajuste significativa, pero en comparación con el modelo cuadrático, menos significativa

La falta de ajuste indica que los modelos no son buenos predictores, debido a que las réplicas que se realizaron corresponden ha experimentos independientes y al analizar el gráfico de transformaciones de potencia (Box Cox) para determinar si se debe realizar transformación de los datos, el gráfico de Box Cox (Véase figura 4) indica que no se requiere, tanto para el modelo cuadrático (lambda= 1,0) como para el cúbico especial (lambda= 1,0); además, que para mejorar el ajuste y la precisión se deben realizar réplicas en algunos puntos. Al observar el Leverage dado por la matriz Hat (Véase tabla 8), podemos ver que sus valores más altos se encuentran para los puntos ubicados en las caras del poliedro, lo que sugiere que son posibles candidatos para ser replicados, permitiendo la mejora del modelo.

Figura 4. Análisis de la gráfica de Box Cox para determinar si se deben hacer transformaciones a los datos (a) modelo cuadrático, (b) modelo cúbico.

A pesar de que los valores del Leverage en la matriz no son altos para los puntos ubicados en los centros de las caras del poliedro, sí se podría esperar que la posible replicación de estos puntos pudiera mejorar la falta de ajuste y, por ende, la precisión en los valores estimados.

Tabla 8. Valores derivados de la matriz Hat (X'X)^-1.

Dureza

Los valores de la dureza mostraron ser bastantes homogéneos, a pesar de que la formulación 1 tuvo un valor promedio por encima de la especificación, este puede atribuirse ha ajuste de la máquina tableteadora que a la formulación en sí.

Según la suma de cuadrados tipo I (Véase tabla 9), el modelo canónico cúbico especial representa la mejor respuesta de superficie, y el modelo cúbico presenta problemas de confusión. Para determinar cuál modelo es el más adecuado se procede a verificar la falta de ajuste para todos los modelos.

Tabla 9. Suma de cuadrados tipo I para el modelo secuencial.

Prueba de falta de ajuste

La prueba de falta de ajuste muestra que, para el modelo canónico cúbico especial, ésta es no significativa, lo que indica que este es el mejor modelo que representa la superficie de respuesta en la región de restricción dada por los pseudocomponentes en la formulación. Que el valor p (<0,0001) sea inferior a 0,05, indica que al menos uno de los términos del modelo es significativo.

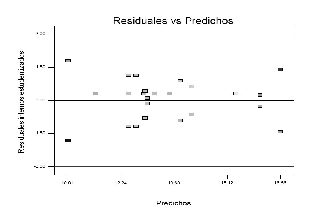
El valor F y el valor p (Véase tabla 10) indican que la falta de ajuste es no significativa; por tal razón se asume que el modelo es adecuado, lo que se ve confirmado por el gráfico de probabilidad normal (Véase figura 5). La figura 6 muestra que los residuales siguen una distribución normal, lo que indica que el modelo es adecuado; además, que no se deben hacer transformación de los datos.

Tabla 10. Análisis de varianza (ANOVA) para la mezcla bajo el modelo cúbico especial.

Figura 5. Gráfico de probabilidad normal.

Figura 6. Gráfico de Residuales vs Valores predichos.

La figura 7 muestra que la varianza es constante al exhibir un comportamiento aleatorio de los datos sobre el gráfico. El gráfico de residuales externos estudentizados en la figura 7 no muestra datos atípicos, lo que indica que no existen efectos de la corrida en el modelo, o que se requiera realizar transformación de los datos.

Figura 7. Gráfico de residuales externos estudentizados.

La ecuación para el modelo, en términos de los pseudocomponentes, es la siguiente:

El valor de R² ajustado (0,8916) indica que 89,16% de la variación existente alrededor de la media es explicada por el modelo. El valor del R² predicho (0,7805) indica que el modelo es un buen predictor para la variable respuesta, lo cual se ve confirmado por la razonable concordancia (diferencia inferior a 0,20) entre el R² ajustado y el R² predicho. El valor de la precisión adecuada (13,764) muestra que hay poca asociación entre el error y la respuesta relativa predicha (se espera que el valor sea mayor a 4), es decir, el ruido no afecta la respuesta (Véase tabla 11).

Tabla 11. Estadísticos de la regresión para la dureza.

Figura 8. Gráfico de contorno y tridimensional para la región de restricción cuando X₄ (lactosa) toma el valor medio (X₄ = 0,3462).

Friabilidad

Los valores para la friabilidad estuvieron todos por debajo de la especificación, lo cual permite considerar como efectivas estas formulaciones para conservar la integridad de la tableta en su transporte y manipulación y garantizando así la no pérdida del principio activo por desgaste.

La suma de cuadrados tipo I (Véase tabla 12) muestra que el modelo canónico cúbico especial es el que mejor explica la superficie de respuesta.

Para determinar cuál modelo es el más adecuado se procede a verificar la falta de ajuste para todos los modelos.

Tabla 12. Suma de cuadrados tipo I para el modelo secuencial.

Prueba de falta de ajuste

La prueba de falta de ajuste muestra que, para el modelo cúbico especial, esta no es significativa, lo que lo señala como el mejor modelo que representa la superficie de respuesta en la región de restricción dada por los pseudocomponentes en la formulación (Véase tabla 13).

Tabla 13. Análisis de varianza (ANOVA) para la mezcla bajo el modelo cúbico especial.

Puesto que el valor p (<0,0001) es inferior a α= 0,05, al menos uno de los términos del modelo es significativo, es decir, el modelo es significativo.

El valor F (0,09) y el valor p (0,7690) indican que la falta de ajuste no es significativa. Por tal razón se asume que el modelo es adecuado, lo cual se ve confirmado por el gráfico de probabilidad normal (Véase figura 9).

Figura 9. Gráfico de probabilidad normal

La ecuación para el modelo en términos de los pseudocomponentes es la siguiente:

El valor de R² ajustado (0,9048) indica que 90,48% de la variación existente alrededor de la media es explicada por el modelo. El valor del R 2 predicho (0,8018) indica que el modelo es un buen predictor para la variable respuesta, lo cual se ve confirmado por la razonable concordancia (diferencia inferior a 0,20) entre el R² ajustado y el R² predicho. El valor de la precisión adecuada (15,242) muestra que hay poca asociación entre el error y la respuesta relativa predicha (se espera que el valor sea mayor a 4), es decir, el ruido no afecta la respuesta (Véase tabla 14).

Tabla 14. Estadísticos de la regresión para la friabilidad.

La figura 10 muestra que los residuales siguen una distribución normal, lo que indica que el modelo es adecuado; además, que no se debe realizar transformación de los datos.

Figura 10. Gráfico de residuales vs Valores predichos.

A pesar de que no se observa comportamiento aleatorio claro en la figura 10, de los residuales internos estudentizados vs los valores predichos, no se puede decir que la varianza no sea constante para el modelo. El gráfico de residuales externos estudentizados en la figura 11 no muestra datos atípicos, lo que indica que no hay efectos de la corrida en el modelo o que hay que realizar transformación de los datos.

Figura 11. Gráfico de residuales externos estudentizados.

Figura 12. Gráfico de contorno y tridimensional para la región de restricción cuando X₄ (lactosa) toma el valor medio (X₄ = 0,3462).

Al realizar una revisión de la bibliografía existente para las formulaciones de Ibuprofeno (10), se encontró que para mejorar la fluidez de las mezclas se utiliza óxido de silicio coloidal como coadyuvante en proporciones del 1%, lo que mejora de manera sustancial la capacidad de flujo pero no afecta las otros parámetros farmacotécnicos de la formulación, como dureza, friabilidad y disolución. La utilización de este lubricante de última generación asociado con el estearato de magnesio (lubricante de elección) estaría en contraposición del objetivo de este estudio, que es el buscar opciones de formulación menos costosas pero que preserven las propiedades del medicamento en cuanto a funcionalidad, e incrementaría el coste final de producción. Ahora bien, como ya se mencionó, las formulaciones reportadas de ibuprofeno, además del óxido de silicio coloidal, utilizan alrededor de 10 excipientes distintos (10) para lograr una formulación óptima. La adición de un excipiente más, como variable fija, es decir, para todas las formulaciones utilizarlo al 1% no implicaría un incremento sustancial del costo final del producto y disminuiría la alta variabilidad en el ángulo de reposo, pero significaría realizar otro diseño experimental para evaluar las posibles respuestas, y así obtener una formulación adecuada para producción a nivel industrial.

Los resultados de dureza están acordes con los valores esperados para la formulación dentro de lo que se considera como parámetros de calidad. Esto quiere decir que el compactante X₃ (excipiente de compactación) cumplió de manera eficiente con su función de generar cohesión entre las moléculas de los distintos componentes de la formulación.

Al evaluar los valores de friabilidad para todas las formulaciones, se observa que estas cumplen con el parámetro establecido que debe ser inferior al 1%, parámetro que indica la capacidad que tienen las tabletas de resistir el desgaste por el roce con las superficies y el que se puede producir contra las paredes del blíster en su empaque final.

Se demostró que es posible formular medicamentos basándose en el diseño de mezclas. Como se mencionó, toda forma farmacéutica es invariablemente una mezcla de componentes. Estos componentes o excipientes y el principio activo cumplen funciones específicas, y el resultado final, que es el medicamento, es la suma de las interacciones de los componentes. Además, se logró demostrar que es posible modificar formulaciones ya existentes buscando un objetivo común, en nuestro caso, disminuir el coste de adquisición de los excipientes al modificar una formulación, y que con pequeñas adecuaciones se puede obtener una formulación óptima de bajo costo.

1. Banker SG, Rhodes CT. Modern Pharmaceutics. 4a Ed. New York: Marcel Dekker; 2002.        [ Links ]

2. Rae Cho B, Shin S, Choi Y, Kovach J. Development of a multidisciplinary optimization process for designing optimal pharmaceutical formulations with constrained experimental regions. Int J Adv Manuf Technol. 2009; 44 (9-10): 841-853.        [ Links ]

3. Martinello T, Kaneko TM, Robles Velasco VM, Santos Taqueda ME, Consiglieri VO. Optimization of poorly compactable drug tablets manufactured by direct compression using the mixture experimental design. Int J Pharm. 2006; 322 (1-2): 87-95.        [ Links ]

4. Campisi B, Chicco D, Vojnovic D, Phan-Tan-Luu R. Experimental design for a pharmaceutical formulation: Optimization and robustness. J Pharmaceut Biomed. 1998; 18 (1-2): 57-65.        [ Links ]

5. Borges CN, Bruns RE, Almeida AA, Scarminio IS. Mixturemixture design for fingerprint Optimization of chromatographic mobile phases and extraction solution for Camellia sinesis. Anal Chim Acta. 2007; 595 (1-2):28-37.        [ Links ]

6. Armstrong NA. Pharmaceutical Experimental Design and Interpretation. 2a ed. Boca Raton: Taylor and Francis Group; 2006.        [ Links ]

7. Lewis GA, Mathieu D, Phan-Tan-Luu R. Pharmaceutical Experimental Design. New York: Marcel Dekker; 1999.        [ Links ]

8. Pinillos JM, Gómez CM. Elaboración de una Formulación Farmacéutica a Través de un Diseño Experimental de Mezclas [Monografía Especialización]. Medellin: Universidad Nacional de Colombia; 2008.        [ Links ]

9. Cornell J. Experiments with Mixtures. 3a Ed. New York: John Wiley & Sons; 2002.        [ Links ]

10. Niazi SK. Handbook of Pharmaceutical Manufacturing Formulation. Compressed Solid Products Volume 1. New York: CRC Press LLC; 2004.        [ Links ]

* Autor a quien debe dirigir la correspondencia: jpinillos@farmacia.udea.edu.co