Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Suma Psicológica
Print version ISSN 0121-4381
Suma Psicol. vol.19 no.2 Bogotá July/Dec. 2012
UNA REVISIÓN DE LAS RELACIONES ENTRE LOS SISTEMAS DINÁMICOS Y LA PSICOLOGÍA DEL DESARROLLO
A REVIEW OF RELATIONS BETWEEN DYNAMIC SYSTEMS AND DEVELOPMENTAL PSYCHOLOGY
Jaime Castro-Martínez
Institución Universitaria Politécnico Grancolombiano, Colombia
Hernán Sierra-Mejía
y Rita Flórez-Romero
Universidad Nacional de Colombia, Colombia
La correspondencia relacionada con este artículo puede ser dirigida a Jaime Castro Martínez, correo electrónico: jcastrom@poli.edu.co
Recibido: octubre 30 de 2012 Aceptado: diciembre 4 de 2012
Resumen
Este artículo tiene como propósito presentar una revisión de las relaciones entre los sistemas dinámicos y las teorías del desarrollo. Para ello, se mencionan ciertos antecedentes de la aparición de los sistemas complejos en psicología, que derivan en su inclusión en la psicología del desarrollo, especialmente con la sinergética y su aplicación al problema del movimiento de Bernstein. Se expone la psicología del desarrollo de Esther Thelen y Paul van Geert, donde se describen diversas propiedades de los sistemas dinámicos no lineales y varios métodos para estudiar el cambio psicológico. El texto finaliza señalando algunas consecuencias de la implementación de esta aproximación y los posibles retos para una ciencia del cambio.
Palabras clave: desarrollo, sistemas dinámicos, variabilidad, caos, sinergética
Abstract
This paper presents a review of relations between dynamical systems and development theories. To do this, mentioned some background of the emergence of complex systems in psychology is mentioned, which result in their inclusion in developmental psychology, especially with the synergetic and its application to the problem of the motion of Bernstein. Explain Esther Thelen and Paul van Geert developmental psychology is explained, which describes various properties of nonlinear dynamical systems and some types of methods for studying psychological change. The paper concludes by pointing out some consequences of the implementation of this approach and potential challenges for a science of change.
Key words: Development, dynamic systems, variability, chaos, synergetic.
Todo investigador del desarrollo, cuando aborda el desarrollo desde cualquier perspectiva, se ve abocado a poner atención sobre qué se desarrolla y cómo lo hace (Granott, 1998). Se ve en la necesidad de clarificar las estructuras y procesos posibles en los cambios y continuidades de las dinámicas tanto individuales como grupales. Desde sus inicios, la psicología del desarrollo se había interesado por dar respuesta a estos dos interrogantes; sin embargo, a pesar de los adelantos en la búsqueda de mecanismos con los cuales describir y explicar dichos cambios, no conseguía explicar la variabilidad intra e intersujeto, en términos macro y microgenéticos, y los cambios abruptos y profundos de la ontogenia.
Inicialmente, bajo un modelo estructuralista Piagetiano, se pensaba que la aparición de estructuras cualitativamente nuevas era el resultado de procesos de adaptación que conducían a reorganizaciones constantes de las estructuras del conocimiento existentes (Piaget, 1969a, 1969b, 1971, 1972; Piaget & Inhelder, 1973). Posteriormente, con los teóricos del procesamiento de la información simbólica, estos cambios tendrían lugar en el nivel de las capacidades de representar el conocimiento, más que en un nivel estructural específico (Klahr, 1992). Y más recientemente, con los teóricos de la especificidad de dominio, aunque se aceptaba que existiesen cambios sistemáticos en las estructuras del conocimiento, estos no eran generales, existiendo diferencias entre dominios específicos del conocimiento (Karmiloff-Smith, 1994).
Estos distintos avances iniciaron una fragmentación conceptual y empírica profunda que paulatinamente dejaba de lado las preguntas por mecanismos generales (Sternberg, 1999). Así, la mayoría de los estudios sobre qué cambia en el desarrollo, se habían centrado en fases relativamente estáticas que analizaban la ejecución infantil y las formas de pensamiento en una edad dada, y comparaban esos hallazgos entre edades (Granott, 1998). Sólo, a medida que se intentaba dar respuesta al cómo, se empezaron a incluir nuevos modelos de investigación sustentados en el microdesarrollo (Granott & Parziale, 2002; Siegler, 1996), conexionismo (Munakata & McClelland, 2003) y sistemas automodificables (Smith & Thelen, 1993), que resaltaban el papel esencial de la temporalidad y de la dinámica de las estructuras en cambio permanente.
A raíz de estas inclusiones, los nuevos teóricos del desarrollo veían la necesidad de introducir en sus trabajos una serie de conceptos referidos, desde la aproximación estructural, a la idea de arreglos u organizaciones que funcionaran como sistemas más generales y sintéticos; y desde una aproximación procesual, a modificaciones autoorganizables y emergentes. De esta forma, la fragmentación teórica, el aislamiento conceptual y la arbitrariedad empírica que caracterizaba a la psicología del desarrollo del momento, daba paso a la búsqueda de un cuerpo de insight compartido, un marco explicativo basado en principios científicos generales (Lewis, 2000b). Es así que, hacia mediados de los 80's autores como Esther Thelen y Alan Fogel, veían en la teoría de los sistemas dinámicos una herramienta con la cual era posible responder a los problemas comunes en la psicología del desarrollo, conduciendo a una primera publicación conjunta sobre su aplicación al desarrollo motor infantil (Thelen, Kelso, & Fogel, 1987), y al desarrollo comunicativo y expresivo temprano (Fogel & Thelen, 1987).
Sistemas complejos en psicología: antecedentes
Los orígenes de la concepción de un orden complejo en la naturaleza, en la era moderna, se remontan a finales del siglo XIX y principios del XX, con la crítica al atomismo de la época, y con la reevaluación del reduccionismo como método científico idóneo en la adquisición de conocimiento (Sawyer, 2002). Pero particularmente se cuenta el desarrollo del álgebra topológica de Poincaré como el primer instrumento con el cual se abría paso a una nueva forma de interpretar el espacio y las relaciones al interior de éste. La naciente ciencia de la complejidad empezaría a incluir elementos de distintas ramas del conocimiento, y a impactar áreas diversas como la fisiología, la geofísica o la economía. Los desarrollos de la teoría de conjuntos en matemáticas, la teoría general de sistemas en biología, o la teoría de las estructuras disipativas en química, entre otras, conformarían una nueva "mirada" de las estructuras y procesos que tienen lugar en todos los campos del conocimiento.
Hacia la década del 70, supuestos de la complejidad, como la teoría de las catástrofes de René Thom (1975), alcanzaban a filtrarse de manera importante en las ciencias sociales, y en particular en la psicología. Los desarrollos de esta teoría llevaron a la aparición de un primer artículo que mostraba la aplicación de la complejidad en las ciencias comportamentales y de la vida (Cobb & Ragade, 1978), y posteriormente se utilizaría en la descripción de fenómenos conductuales y cognitivos (Rose & Fischer, 1998; van der Maas & Hopkins, 1998; van der Maas & Molenaar, 1992a). Conceptos como el de histéresis, el cual hace referencia a la propiedad de una función con una parte "no lineal", que es inaccesible y que se dobla hacia atrás en su curso (Figura 1), se habrían utilizado para interpretar ideas piagetianas como la de discontinuidad (Fischer & Paré-Blagoev, 2000; Van Der Maas & Molenaar, 1992b), y en fenómenos emocionales como la ira y la frustración (Scherer, 2000).
De manera similar, la teoría del caos se empezaría a utilizar a finales de los 80's, y principios de la década de los 90's, para estudiar la conducta humana y el desarrollo (Fabian & Stadler, 1991; Freeman & Skorda, 1990; Heiby, 1992; Li & Xu, 1987; Lonie, 1991; Nelson, 1992; Schmid-Denter, 1992; Skinner, 1989; Thelen & Smith, 1994; van Geert, 1994; Vroon, 1992). Guastello (2000), por ejemplo, divide los aportes iniciales de la teoría del caos en tres campos de la psicología: el referente a la ciencia cognitiva, el campo de la psicología social y organizacional, y el campo de la psicología de la personalidad y psicología clínica. Es así que, a partir de elaboraciones teóricas distintas, como las de Abraham y Gilgen (1995), Robertson y Combs (1995), y de Sulis y Combs (1996), se daría lugar, a mediados de los 90's, a la formación de la Sociedad para la Teoría del Caos en Psicología y las Ciencias de la Vida.
La sinergética de Haken y el problema de Bernstein
Mientras que la teoría de las catástrofes de Thom (1975) iniciaba su incursión en las ciencias sociales, Hermann Haken introducía, en el campo de la física, el concepto de sinergética, con el cual trata de estudiar los procesos de formación de estructuras de los sistemas al disminuir sus grados de libertad, desde lo inestable hacia lo estable (Haken, 1999). La sinergética se convertía en el estudio de la emergencia de estructuras espaciales, temporales, espacio-temporales y funcionales equilibradas, en sistemas complejos, estructuras estables llamadas en muchos casos atractores. Estos son entendidos como lugares en el espacio donde el sistema se estabiliza, cualquiera que sea la condición inicial y cualquiera que sea el camino que el sistema tome para alcanzar el equilibrio (Figura 2).
Para Haken (1999), la autoorganización del sistema se daba por lo que él llamó parámetros de control o de orden. Dichos parámetros cumplían la misión de "esclavizar" ciertos grados de libertad, forzando a los componentes del sistema a comportarse de una manera coherente. La relación que establecen se considera de tipo interactiva, en la medida en que los componentes individuales determinarían el parámetro mismo.
De esta forma, la sinergética llegaba a consolidarse en una herramienta para analizar las transiciones de comportamientos y para resolver los problemas de reconocimiento de patrones, los cuales emergían de la autoorganización del sistema. Con ella se manipularía el desarrollo de una organización caótica, disminuyendo su caoticidad, a través de la reducción del número de atractores del sistema (Haken, 1999; Haken, Kelso, Fuchs, & Pandya, 1990). En este sentido, con la sinergética se daría origen propiamente a la teoría de los sistemas dinámicos.
Posterior a estos adelantos se discutía al interior de las ciencias del movimiento cómo dar respuesta al llamado Problema de Bernstein (Bernstein, 1967; Sporns & Edelman, 1993). Dicho problema consiste en explicar los orígenes del movimiento por fuera de un agente central de control. Para entender el problema de Bernstein hay que considerar que la acción motriz involucra la continua regulación de una miríada de movimientos musculares. Esta característica, que en la literatura se ha llamado "de grano fino", por la especificidad de las estructuras necesarias para el movimiento, sólo podía ser entendida a través de la orquestación de un conjunto complejo. Resultaba evidente que las respuestas de cualquier conjunto de este tipo podrían colapsar cualquier mecanismo de control central, ya que el número de mecanismos subordinados que se necesitarían para ejercer el más mínimo movimiento en un tiempo específico era exageradamente alto (Camras & Witherington, 2005).
Esta perspectiva de un mecanismo de control central llevó a Kelso y otros autores (Kelso, 1981a, 1981b; Kelso & Schöner, 1988a, 1988b; Kelso & Tuller, 1984; Schöner & Kelso, 1988; Turvey, 1990), a adoptar las nociones de Haken para pensar los músculos como ensambles organizados de manera sinergética que pueden operar como un grupo. La carga del control se distribuiría entre procesos de alto y bajo control, y la activación de un solo miembro del ensamble podía conducir a la activación de otros miembros, sin la necesidad de una respuesta específica de un agente de control de orden superior. Desde esta nueva perspectiva, la activación motora era concebida en su mayoría como auto organizada, más que dictaminada en su totalidad por un comando de orden superior (Thelen, 2000b). Es así que el ensamble de sinergias tomaría ventaja de los aspectos no neuronales del movimiento: los efectos de la gravedad, las propiedades elásticas de los músculos y los efectos inerciales (Thelen & Bates, 2003).
La perspectiva de ensambles auto organizados eliminaba los planes o programas codificados en un agente de control central. Dejaba de lado el asunto de la pre programación genética para hablar de estructuras coordinativas en los sistemas motores que trabajarían como grupos funcionales de músculos y uniones, cuya coordinación mutua era regulada sinérgicamente por el sistema funcionando como un todo (Fogel & Thelen, 1987). En sentido estricto, estas estructuras coordinadas eran vistas como una clase especial de sistema termodinámico, un sistema disipativo no lineal que usaba energía para mantener la complejidad (Kugler, Kelso, & Turvey, 1980).
Tales adelantos tendrían dos consecuencias importantes para la psicología del desarrollo de la época: por un lado, mostraban al movimiento como un sistema dinámico, lo cual permitía interpretar su desarrollo bajo esta misma característica, y por otro, utilizaban el parámetro de orden como un concepto válido para entender la variabilidad y la estabilidad de un sistema en constante cambio, lo que había sido un problema para los teóricos del desarrollo hasta ese momento. Estas formas de apreciar la propuesta de Haken y de los sistemas dinámicos conducirían, finalmente, a la conformación de las dos corrientes más importantes en la utilización de los sistemas dinámicos en la psicología del desarrollo: la corriente de Bloomington y la de Groningen y, a un sinnúmero de aplicaciones en otros campos psicológicos.
El inicio de los sistemas dinámicos en la psicología del desarrollo
En un primer momento Thelen y otros autores (Hofsten, 1989; Kamm, Thelen, & Jensen, 1990; Thelen, 1985, 1995; Thelen & Smith, 1994) utilizaron algunos de los principios de los sistemas dinámicos para explicar la ontogenia y la auto organización de la acción motriz infantil, proponiendo que el desarrollo de nuevas habilidades motoras resultaba de cambios en sus componentes, los cuales se hallaban relacionados de manera sinérgica, más que en la maduración de un programa motor predefinido. La propuesta inicial se encontraba orientada a demostrar que algunos fenómenos comportamentales, como la actividad motriz, no podían ser explicados fácilmente por las teorías tradicionales basadas en maduraciones tempranas.
Los primeros trabajos de esta autora en niños pequeños, sobre las dinámicas del movimiento, habían demostrado la multicomponencialidad de la conducta de caminar, el desarrollo diferencial de estos componentes y la sensibilidad a eventos orgánicos y medioambientales (Thelen, 1984). A partir de estos desarrollos, Esther Thelen, de la Universidad de Indiana, en Bloomington, utilizaría de manera descriptiva ciertas propiedades de los sistemas dinámicos, como la complejidad, la auto organización, la estabilidad dinámica y atractividad, los cambios y transiciones de fase, y las relaciones en escalas de tiempo, para entender el desarrollo motor infantil (Thelen & Smith, 1994; Thelen & Ulrich, 1991), pero quizá ha sido su consideración de las escalas de tiempo y el uso de escenarios topológicos, sus inclusiones conceptuales y metodológicas más relevantes al campo de la ciencia del desarrollo.
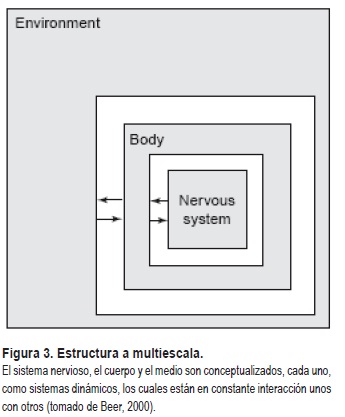
Uno de los principales usos de los fundamentos de los sistemas dinámicos llevado a cabo por esta autora estuvo en la determinación de escalas de tiempo interrelacionadas y mutuamente graduadas (Thelen & Smith, 1994). Dentro de los primeros supuestos de los sistemas dinámicos se dice que los organismos en desarrollo son sistemas complejos, compuestos de muchos elementos individuales embebidos o incrustados unos dentro de otros, y abiertos a un medio ambiente complejo. Esta diferenciación de elementos, subsistemas y relaciones entre elementos de muy diverso tipo, por efecto de la auto organización, puede generar estructuras a multiescala, es decir, patrones de inclusión sucesiva de unos sistemas en otros, a través de distintos niveles jerárquicos (Figura 3).
Otro supuesto importante es que los cambios ocurren en diferentes escalas de tiempo. La excitación neuronal ocurre en milisegundos, los tiempos de reacción son del orden de cientos de milisegundos, las personas aprenden habilidades después de horas, días y meses de práctica, los cambios en el desarrollo ocurren en el transcurso de semanas, meses y años, y la evolución durante un periodo de tiempo mucho mayor. Todas estas escalas podrían acoplarse, por ejemplo, en una propuesta de estudio compleja de un aprendizaje específico. Desde la perspectiva de los sistemas dinámicos, considerar cada proceso por separado es erróneo. Las escalas de tiempo deben ser unificadas y coherentes, al igual que los elementos interactuantes del sistema (Smith & Thelen, 2003).
Bloomington: aportes conceptuales y metodológicos
A continuación se presentarán algunos de los aportes señalados de la perspectiva de Bloomington.
Escalas de tiempo: tiempo real vs tiempo del desarrollo
El primer aporte importante de la escuela de Bloomington está en la reconceptualización de los tiempos del desarrollo. En esencia, Thelen nos habla de dos tiempos (Thelen & Smith, 1994). El primero es el llamado tiempo real, el aquí y el ahora, los segundos y fracciones de segundos de la conducta inmediata. Según la autora, cada acto es una forma de conducta nueva: estable y predecible en algunas de sus características, pero variable, flexible y adaptativa en cada instancia. Para esta autora, la piedra angular de la teoría dinámica del desarrollo es esta naturaleza emergente de la conducta acoplada en tiempo real. El segundo tiempo es el tiempo de la ontogenia o del desarrollo. Con el desarrollo, la estabilidad de algunas formas puede aumentar o disminuir, pero el acoplamiento dinámico de las conductas permanece constante.
En los sistemas psicológicos, las escalas de tiempo comúnmente incluyen la emergencia de la conducta en tiempo real y la emergencia de hábitos conductuales en tiempo del desarrollo (Lewis, 2000a, 2002). Así, procesos en una escala influencian procesos en otra. La coherencia del tiempo y los niveles de los sistemas complejos significan que las dinámicas de una escala de tiempo deben ser continuas con, y estar anidadas en, la dinámica de todas las otras escalas de tiempo (Smith & Thelen, 2003). Esta consideración es importante cuando se quiere abordar un fenómeno psicológico. Por ejemplo, Lewis (2000a, 2002), para estudiar la auto organización emocional, se basa en tres niveles del desarrollo emocional: el nivel de los episodios, el referido a los estados de ánimo, y el nivel de la personalidad. Cada uno se diferencia por la escala de tiempo adoptada: la primera iría de segundos a minutos, la segunda de horas a días, mientras que el nivel de la personalidad implicaría un tiempo de años de construcción. Esta visión de la temporalidad ha conducido a una interpretación de los procesos temporales del desarrollo en términos de microdesarrollo, mesodesarrollo y macrodesarrollo (Valsiner, 2006). Cada uno de estos niveles se caracterizaría por poseer una unidad de tiempo funcional propia. Según Valsiner (2006) la microgénesis, por ejemplo, estaría limitada a la transformación del desarrollo que ocurre en milisegundos. Mientras que la ontogenia, vinculada más directamente al mesodesarrollo, estaría restringida al tiempo de vida del organismo. Esta forma de ver los procesos en distintos niveles implica una comprensión de los fenómenos en paralelo, una nueva forma en la ciencia de abordar las estructuras y procesos complejos. Según este autor, lo importante en todo caso es conservar la interacción de los niveles en las distintas escalas de tiempo. Las diferentes consideraciones sobre las dinámicas temporales rescatan la posibilidad de la autosimilitud entre escalas.
Graficación de escenarios de cambio
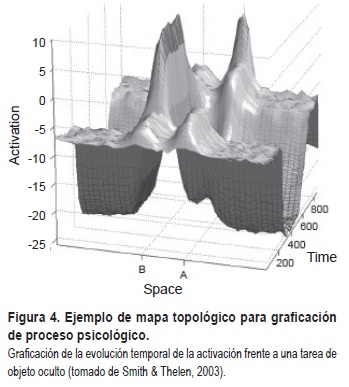
El segundo aporte importante de la inclusión de Thelen y la corriente de Bloomington en los sistemas dinámicos es el uso de paisajes o escenarios topológicos para describir las modificaciones en la ejecución de ciertas tareas (Figura 4). Thelen y otros autores (Gershkoff-Stowe & Thelen, 2004; Schutte, Spencer, & Schöner, 2003; Smith & Thelen, 2003; Spencer & Schöner, 2003), en un intento por aplicar la característica de campo de los sistemas dinámicos, utilizaron este método para describir la ejecución de varios niños en la llamada tarea de búsqueda del objeto oculto, la cual hace referencia a una tarea típica de permanencia de objeto. La tarea consiste en ocultar un objeto en un lugar A. Tras un tiempo especificado por el investigador se le permite al niño buscar el objeto. La siguiente parte de la tarea consiste en mover el objeto de un lugar A a uno B. El "error" común del niño es buscar el objeto en A y no en B, aunque su mirada puede variar de un lugar a otro (Figura 4).
Thelen interpreta las variaciones en los mapas topológicos como las diferencias en la activación (arousal) del niño frente a la tarea. La activación no sería del tipo todo o nada, sino que, por el contrario, aumenta y decae gradualmente. Para la autora, estas modificaciones en los niveles de activación juegan un papel importante en los cambios del desarrollo frente al comportamiento de la tarea. Lo que ésta y otros autores han encontrado es que la ejecución de dicha tarea depende especialmente de los inputs visuales y de procesos de memoria. Tras muchos ensayos la búsqueda del objeto variará de A a B (Spencer, Smith, & Thelen, 2001; Thelen, 2000a), (Figura 5).
Igualmente para Thelen, el error A-no B es mejor explicado por la teoría de la acción situada, en la cual un sujeto corpóreo o psicológico, no un sujeto epistémico, actúa con la ayuda y constricción de un mundo físico que envuelve el medioambiente externo y las propiedades físicas del cuerpo, incluyendo el cerebro. En la llamada Teoría del Campo Dinámico la representación del bebé de las localizaciones espaciales se relaciona con un campo sostenido de pesos de activación en el cerebro. De acuerdo a Thelen y sus colegas (Thelen, Schöner, Scheier, & Smith, 2001), el modelo se aplica a la acción real en objetos físicos en espacio y tiempo real. Para Thelen, hablar de representación desde esta psicología es innecesario, por cuanto que la cognición es un sistema dinámico complejo que percibe y actúa en el mundo en tiempo real, sin una representación dada (Smith, 2005).
La autora complementa esta serie de teorías con la llamada Teoría de la Corporalización (Embodiment), sobre la cual sostiene la importancia de pensar la cognición a través del movimiento corporal. La hipótesis de la corporalización supone que la inteligencia emerge en la interacción de un organismo con un medio, y como el resultado de la actividad sensoriomotriz. Esta hipótesis sugiere que todo el conocimiento emerge, se incrusta, distribuye y no se separa de los procesos en tiempo real, de percibir, recordar, atender y actuar (Samuelson & Smith, 2000). La cognición, desde esta perspectiva teórica, es un conjunto complejo de procesos internos que se afectan mutuamente y se dirigen al mundo a través de la percepción y la acción en tiempo real, sin representaciones fijas y segregadas de ningún tipo. La cognición sólo sería un sistema dinámico complejo.
El uso de este método ha tenido implicaciones importantes en otras áreas del desarrollo. Lewis y colaboradores (1999), por ejemplo, utilizan la técnica de graficación en una rejilla espacio estado (State space grid) como método espacio-temporal para ubicar atractores en el comportamiento de un niño frente a la separación de su madre en diversas etapas de su desarrollo (de 2 a 6 meses). La alta estabilidad del atractor, visualizada en la integración de las partes del mismo en la rejilla, se muestra en unas edades (entre los 3 y los 6 meses), pero no antes (Figura 6). Estos trabajos también demuestran la alta variabilidad en el comportamiento entre individuos, ya que la forma de los atractores y la aparición de los mismos varía de un niño a otro y de una etapa a otra.
Groningen y la corriente europea de los sistemas dinámicos
Paralelamente a estos avances, hacia principios de los 90's, Paul van Geert, de la Universidad de Groningen, Holanda, vería igualmente en los conceptos de sinergética y parámetros de orden de Haken, una forma de estudiar el desarrollo lingüístico temprano (van Geert, 1991). Para van Geert, la increíble complejidad del cerebro y la correspondiente complejidad del mundo son caracterizados por patrones complejos, parámetros de orden, que emergerían de las interacciones entre organismos y medios (van Geert, 1994).
Modelos de Fisher & Dawson
Van Geert inicia su incursión por los sistemas dinámicos utilizando el componente matemático de los mismos para generar modelos que simulan el desarrollo en diversas áreas de la psicología. En particular, este autor inicia sus desarrollos conceptuales utilizando el modelo de crecimiento logístico, que corresponde a uno de los cuatro modelos descritos por Fischer y Dawson (2002) para explicar el desarrollo lingüístico, cognitivo y socioemocional. A continuación se presenta brevemente cada uno de estos modelos:
Modelo de ecuación estructural. A partir de los trabajos de Kaplan (2000), estos modelos se basan en la regresión lineal, la cual es una herramienta que compara diferentes modelos de relación lineal entre medidas y/o constructos. Se dice que los tipos de ecuación estructural no son óptimos para responder a muchas de las preguntas del desarrollo debido a sus presupuestos lineales y a su falta de enfoque en los patrones del cambio (Fischer & Dawson, 2002).
Modelo de crecimiento lineal. Estos son modelos de ecuación estructural modificados para aplicarse a problemas de crecimiento (Duncan, Duncan, Strycker, & Li, 1999), los cuales incluyen el modelo de crecimiento latente y usan la función de crecimiento de cada persona como su unidad de análisis.
Modelo de crecimiento logístico. A diferencia del modelo anterior introduce la visualización de los cambios no lineales. Con este modelo se reconoce que la mayor parte del desarrollo envuelve cambios no lineales que surgen de la dinámica de crecimiento. El crecimiento logístico se basa en la ecuación estándar de crecimiento usada en las ciencias biológicas, en la cual la curva básica es en forma de S en vez de una curva lineal.
Modelo de crecimiento dinámico. Estos modelos eliminan el presupuesto lineal de la mayoría de los análisis estadísticos y conllevan a que los patrones de crecimiento tomen formas más complejas. Las herramientas estadísticas se centran en un grupo de patrones, pero el modelamiento de crecimiento mueve el análisis hacia la curva de crecimiento de los individuos, tomando cada curva individual como la unidad base. Cuando las complejas curvas de crecimiento individual son promediadas entre muchos individuos, resulta, generalmente, una curva alisada única, pero desafortunadamente esta curva no representa de manera precisa los patrones de crecimiento individual (Demetriou & Raftopoulos, 1999).
En general, un modelo de crecimiento dinámico da cuenta explícitamente del principio de causalidad mutua o recíproca. En él se concibe el desarrollo como una red de componentes en interacción, basados en relaciones de soporte, relaciones competitivas y condicionales. Las relaciones son recíprocas pero no necesariamente simétricas. Al modelar tales redes de acción recíproca es posible comprender la emergencia de estados, regresiones temporales, crecimiento en forma de U invertida, oscilaciones, zigzags y crecimiento en forma de S (Gershkoff-Stowe & Thelen, 2004; Thelen & Ulrich, 1991; Yan & Fischer, 2002; Zanone & Kelso, 1991).
De igual forma, los modelos dinámicos no lineales pueden ser usados para marcar diferencias individuales en las curvas de crecimiento. Esto se debe a que las ecuaciones que describen los sistemas cambiantes son sensibles a los valores iniciales, es decir, las trayectorias de las organizaciones dependen de las condiciones iniciales del sistema. Aún si dos conjuntos de condiciones iniciales son ligeramente diferentes, en los sistemas dinámicos no lineales sus estados divergirán rápidamente. Las curvas de crecimiento que describen el desarrollo de dos individuos, cada una caracterizada por el mismo parámetro pero con diferentes valores iniciales, podrían mostrar marcadas diferencias sobre muchas iteraciones (Howe & Lewis, 2005). Desde esta perspectiva de modelo, para capturar las propiedades de la dinámica de relaciones, las medidas que se hagan deben cumplir con los siguientes requisitos:
En primer lugar, la medida debe ser repetida con tal frecuencia (intervalos entre las medidas) que la característica variabilidad de una persona pueda determinarse (el rasgo característico en el cual el puntaje de la persona variará). Este rango es el producto de la variación del contexto característico de la persona, pero también de la variabilidad inherente a las condiciones internas. En segunda instancia, la variable medida debe ser distribuida a través de la persona y las características contextuales de la misma. La naturaleza distribuida a menudo coincide con el funcionamiento de la persona en modos muy específicos. La medida implica que los modos particulares de operación son examinados en forma de pruebas múltiples en varios contextos.
Se dice que los modelos utilizados en particular en la psicología del desarrollo se establecen idealmente para dar cuenta del desarrollo porque ellos pueden "ajustar" las continuidades y discontinuidades que surgen en el devenir. La estabilidad de una estructura del desarrollo puede ser alterada de forma tal que algunos estados llegan a ser menos preferidos y menos confiables, mientras que otros resultan más estables y dominantes. Estas discontinuidades son capturadas en los modelos de sistemas dinámicos usando la noción de transición de fases mencionada anteriormente.
La ecuación de crecimiento cognitivo
Utilizando los modelos anteriores, van Geert define el crecimiento como un incremento cuantitativo catalítico en una variable creciente, siguiendo la emergencia de una posibilidad estructural específica en el sistema cognitivo (van Geert, 1991, p.1), y utiliza el crecimiento logístico más específicamente en la interpretación del crecimiento del vocabulario. van Geert (1991) menciona la existencia de tres propiedades del crecimiento cognitivo: (a) El incremento debe ser autocatalítico, es decir, no se debe dar por impedimentos extrínsecos. El crecimiento es regido por sí mismo, cualquier incremento que importe la mera adición de una fuente externa no es un crecimiento genuino. (b) Debe ser cuantitativo. El crecimiento es una propiedad de una variable. El valor de cada una debe ser expresado en términos de un número entero o fraccionario, aunque se acepta que el crecimiento puede ser usado para describir cambios cualitativos tales como el desarrollo estructural. (c) El desarrollo debe seguir una posibilidad estructural del sistema cognitivo, es decir, el desarrollo debe estar inscrito en un modelo estructural específico que provea interpretaciones cognitivas puntuales de los datos observados. A partir de estas características van Geert presenta la siguiente ecuación de crecimiento (Steenbeek & van Geert, 2005):
Lt+1 = Lt (1 + r - r * Lt /K)
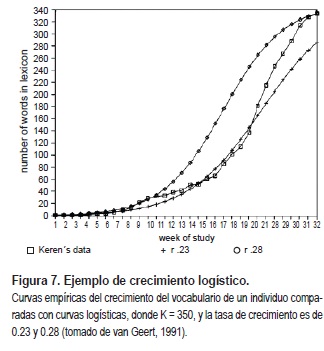
Esta ecuación describe cómo un nivel de crecimiento posterior (Lt+1), en un tiempo (t + 1), es causado por un nivel de crecimiento anterior (Lt), en un tiempo (t), y por dos parámetros adicionales r y K, en donde r representa la tasa de crecimiento y K una constante. La ecuación genera una secuencia de niveles de crecimiento que se siguen unas a otras y forman una curva de crecimiento (Figura 7). Otros ejemplos del uso de ecuaciones logísticas similares se pueden hallar en las investigaciones del mismo autor sobre el juego diádico (Steenbeek & van Geert, 2005).
A partir de estos modelos, la corriente de Groningen desarrolló una línea interesada en el estudio de las discontinuidades y variabilidades del desarrollo. Hasta ese momento las teorías convencionales habían considerado la variabilidad como ruido, errores en las medidas que enmascaraban el verdadero fenómeno pero que podían eliminarse con métodos investigativos apropiados. Siegler (1996) mostró la prevalencia y valor de la variabilidad y su papel eminente en el desarrollo. Reveló que la variabilidad es constante no sólo entre dominios, como alegaba la especificad de dominio, sino también al interior de los mismos, ya fuese entre niños o en un niño en particular. La variabilidad existía entre tareas al interior de un dominio, entre objetos al interior de una tarea, entre presentaciones de un mismo objeto, y aún, en una única presentación de un único objeto. La variabilidad, así, era vista como una fuerza potencial que conducía o encausaba el desarrollo, y como un indicador, también potencial, de los procesos del devenir.
Poco a poco la variabilidad llegaría a ser el centro de atención no sólo por su prevalencia sino por su papel importante para explicar el desarrollo (Granott, 1998). El incremento del interés por los aspectos irregulares del cambio es visible en las investigaciones que se vinculan al estudio del desarrollo motor, lingüístico y emocional. Los investigadores en estos campos perciben la variabilidad comportamental como un precursor de nuevos repertorios conductuales (Bertenthal, 1999; Thelen, 2000b).
Las investigaciones dirigidas al estudio del desarrollo emocional, por ejemplo, presentan indicios de que los niños despliegan conductas variables tanto al interior de las observaciones como entre ellas (de Weerth, van Geert, & Hoijtink, 1999). A su vez, la variabilidad no se restringiría a los individuos sino que también se podría percibir en las interacciones emocionales iniciales (de Weerth & van Geert, 2002; Fogel, 1988; Fogel, Toda, & Kawai, 1988; Granic & Lamey, 2002; Lavelli & Fogel, 2002, 2005). La variabilidad, según estas investigaciones, le asegura al niño una atención maternal continua (de Weerth & van Geert, 1999). Pero a medida que el niño crece la variabilidad puede disminuir como forma de estabilizar ciertos patrones conductuales y rasgos cognitivos que le permiten desenvolverse más ágilmente en el mundo. En el desarrollo del lenguaje, las investigaciones han develado que éste se caracteriza por enormes fluctuaciones. Ruhland y van Geert (1998), igualmente muestran que las formas de las curvas finales en el desarrollo lingüístico poseen grandes diferencias interindividuales, al tiempo que todos los niños mostrarían fuc-tuaciones considerables en su propio desarrollo del lenguaje.
Modelos de estudio de la variabilidad: el uso de datos de tiempo serial
A partir de estas consideraciones sobre la variabilidad, van Geert y van Dijk (2002; van Dijk, 2004) presentan diversas técnicas, esencialmente descriptivas, usadas para analizar tanto la tendencia general como la variabilidad, y que pueden aplicarse en muchas clases de datos de series de tiempo del desarrollo individual. A continuación se presentan algunas de ellas:
Técnicas de graficación de variables cualitativas y cuantitativas. Si partimos de que la variabilidad puede ser tanto cuantitativa como cualitativa, para el caso de la variabilidad cuantitativa cada medida consiste de un nivel en una dimensión única. La variabilidad en este tipo de datos puede ser fluctuante, y la fluctuación es posible de diagramar en una gráfica continua (Figura 8).
Para el caso de una variable cualitativa, cada medida consiste de un conjunto de conductas las cuales tienen, cada una, una ocurrencia específica. La diferencia fundamental entre las variables cualitativas y cuantitativas radica en una dimensión adicional. No sólo habría diferencias en el nivel de las medidas de las variables sino que también variables completamente nuevas pueden ser introducidas. Estas discrepancias en las medidas son expresadas en un gráfico de barras apiladas (Figura 9).
Técnica de Dato Crudo y de Alisamiento. Esta técnica coloca los datos en un diagrama único X-Y, generando un gráfico similar al mostrado en la Figura 8; además, con esta técnica se trata de visualizar la tendencia del desarrollo en los datos usando un polinomio de segundo grado, es decir, una ecuación algebraica que represente una línea de tendencia como la observada en la gráfica. Mientras que los datos en el diagrama X-Y son más bien variables, la línea de tendencia es complemente alisada. Sin embargo, esta técnica conduce a pérdida de información que puede ser valiosa. En muchos casos se utiliza cuando la variabilidad es considerada de poca relevancia (Figura 10).
Graficando la variabilidad: movimiento de mínimos, máximos y promedios. Esta técnica intenta mantener los datos de la variabilidad alrededor de una tendencia general. Los datos son presentados en un ancho de banda de puntajes. Este método utiliza una ventana móvil, un marco temporal que se mueve de una posición a otra. Cada ventana solapa parcialmente la ventana precedente. Una vez diagramado se inspecciona visualmente si muestran fluctuaciones considerables en el tiempo. Adicional a este gráfico se pueden agregar valores de mediana o combinar con la técnica de alisamiento (Figura 11). Dicha técnica es altamente sensible a valores extremos.
Graficando la variabilidad: líneas de altitud.
Este método permite un estudio más a profundidad de la distribución de los valores en el rango. La técnica incorpora las posiciones intermedias en un gráfico de líneas de altitud, en el cual no sólo se diagraman los valores mínimos y máximos en la ventana móvil, sino también los segundos, terceros y demás valores más altos, luego se conectan los correspondientes datos puntuales por una línea (Figura 12). En principio, las líneas de altitud pueden ser interpretadas de la misma forma que las líneas geográficas que representan la altitud y las inclinaciones de un relieve físico.
Graficando la variabilidad: técnica de progmaxregmin. Este método conserva los valores altos y bajos en los casos en que sea necesario mantener esta información. El método consiste en seleccionar una ventana en la cual se tienen un número específico de datos, y se computa el valor máximo para esa ventana. Cuando se incrementa la ventana con otro dato puntual, se mantiene el punto inicial constante y se computa el valor máximo del periodo de la ventana extendida, y así sucesivamente hasta tomar todos los datos. El proceso es reversivo. Iniciando con el último dato se computa el valor mínimo y se realiza el procedimiento anterior. Haciendo esto se tiene una serie de datos de máximos progresivos y mínimos regresivos, lo que se aproxima al concepto matemático de "casco convexo". Este método muestra el rango seleccionado a través de un periodo de tiempo único.
Las distintas técnicas, aquí señaladas, son utilizadas por van Geert para obtener una primera impresión de la tendencia general de las curvas del desarrollo y la forma como la variabilidad se encuentra relacionada con esta tendencia. Según algunos autores (Lewis, 2000b) una aproximación más certera de los sistemas dinámicos a la psicología del desarrollo implicaría el uso de múltiples técnicas y modelos teóricos, por lo cual se recomienda la combinación, por ejemplo, de las técnicas de graficado propuestas por van Geert, más las técnicas de graficado topológico presentadas por Thelen, además de la incorporación de modelos dinámicos, ya sea a través de ecuaciones de crecimiento logístico o cualquier otra ecuación dinámica.
Presentado el marco actual de las dos corrientes principales que han incorporado los sistemas dinámicos al desarrollo, resta aclarar algunas de las consecuencias específicas y los posibles retos para una ciencia del cambio.
Conclusiones
La perspectiva de los sistemas dinámicos ha traído consigo aportes importantes a la psicología del desarrollo, tanto teórica como metodológicamente. Las dos escuelas, antes señaladas, han permitido ampliar el panorama de los estudios del desarrollo al reconsiderar los principios comunes al desarrollo mismo, principios que se expresan a través de la complejidad, la irreversibilidad, y la multicomponencialidad. Esta perspectiva resalta aspectos clave como la variabilidad del desarrollo y las escalas temporales distintas en las que tiene lugar la evolución de los fenómenos, tanto de orden macrogenético como microgenético. Igualmente, ha permitido el avance de metodologías para el estudio del desarrollo, ya sea a través de la graficación de escenarios de cambio por medio de mapas topológicos, o a través de ecuaciones de análisis de series de tiempos que permiten observar la variabilidad tanto individual como interindividual.
Valsiner (2006), por ejemplo, menciona cuatro características del desarrollo psicológico que, con la inclusión de esta nueva perspectiva, llegan a ser resaltadas:
La complejidad de las estructuras y procesos en desarrollo
Con la propuesta de los sistemas dinámicos el desarrollo deja de ser un proceso de relaciones lineales, o una simple suma de componentes, para convertirse en una especie de transformación altamente compleja. Las dinámicas del desarrollo empezarían a mostrar una alta sensibilidad a las condiciones iniciales y grandes cambios a largo plazo. Ejemplos de esta sensibilidad se pueden encontrar en el estudio de las trayectorias de vida de individuos en condiciones aparentemente similares (condiciones socioeconómicas, familiares, escolares, etc.) las cuales divergen significativamente a partir de cambios mínimos en sus historias de vida (Valsiner, 2006; Fogel, 1999).
La irreversibilidad del tiempo del desarrollo
A partir de la consideración de la entropía, como parte del marco de la complejidad en el cual se incluye los sistemas dinámicos, el desarrollo llega a ser irreversible, en el sentido de que, una vez que una nueva estructura emerge, o se alcanza un nivel de crecimiento, el organismo no se revierte a formas tempranas (Valsiner, 2006; Prigogine, 1973, 1976). Es claro que ciertas funciones pueden declinar con la edad o con ciertas patologías, pero los procesos del desarrollo no llegan a deshacerse.
Interacción a varios niveles
Con los sistemas dinámicos se hace aún más evidente la necesidad de interrelacionar diversos niveles explicativos en el desarrollo infantil y adulto. En el desarrollo emocional, por ejemplo, ya no sólo se visualiza el interjuego del niño con la madre, como marco descriptivo del desarrollo mismo, sino que también se incluyen los cambios y variaciones a nivel de las estructuras cerebrales en un tiempo real, tanto de uno como de otro, además del nivel de las modificaciones en tiempos mayores que explicarían la consolidación de personalidades emocionales más o menos estables (Valsiner, 2006; Lewis, 2002, 2005).
La variabilidad de las acciones y comportamientos
Por último, las teorías de los sistemas dinámicos colocan a la variabilidad en el centro del estudio del desarrollo. La comprensión de las variaciones en las ejecuciones por parte de un individuo, o entre individuos, es ahora más fácilmente manejable con cualquiera de las técnicas descritas anteriormente, y los desfases del desarrollo no son ya causa de discusión entre los teóricos modernos (Valsiner, 2006; Siegler, 1994; van Dijk, 2004).
Discusión
Un efecto interesante de la inclusión de los sistemas dinámicos se encuentra en la reconsideración de las teorías clásicas del desarrollo, como la teoría piagetiana o vygotskiana. Para van Geert (1998, 2000), por ejemplo, la variabilidad y la estabilidad relativa son explicables a través de mecanismos generales identificables en las tesis piagetianas y vygotskianas. Según Piaget (1969b) cada encuentro de un sujeto con la realidad resulta en una adaptación dual del sujeto a esa parte de la realidad. Primero, involucra una asimilación de la realidad encontrada a los procedimientos existentes de acción o comprensión en el niño. Segundo, involucra una acomodación de los procedimientos internos existentes a alguna de las exigencias de la realidad con la cual la persona es confrontada.
De esta forma, hay siempre algo nuevo en la realidad que experimentamos, pero la naturaleza de esta novedad co-depende de lo que somos capaces de acomodar. Vygotski (1989), por su parte, propone un principio dual comparable. Para este autor existiría una diferencia entre lo que un niño puede lograr cuando actúa por sí mismo (nivel de desarrollo actual) y cuando el mismo niño puede hacerlo con ayuda de otras personas más competentes (nivel de desarrollo potencial). Las diversas formas de soporte o ayuda son gradualmente incorporadas en la propia competencia infantil, trasformando el nivel potencial en un futuro nivel de desarrollo actual. Este rango de diferencia, entre lo que el niño puede hacer con y sin ayuda, fue llamado por Vygotski la zona de desarrollo próximo o proximal (ZDP).
van Geert (2000) recapitula las tesis piagetiana y vygotskiana para hablar de modelos del desarrollo en donde fuerzas conservativas incrementan la fortaleza de cualquier proceso interno, a través de una experiencia particular, y donde fuerzas progresivas incrementan la fortaleza del procedimiento interno que cae en la intersección entre la novedad y la familiaridad. Estas consideraciones no sólo incorporan teorías anteriores y relevantes a éste nuevo marco, sino que también reviven el interés por encontrar mecanismos que controlan, encausan o direccional el desarrollo. A pesar de los grandes avances en la teoría y métodos de los sistemas dinámicos, aún quedan grandes retos por superar e interrogantes por resolver. Podemos reducir estos a dos grandes campos: el ontológico, referido a la causalidad, y el epistémico, relacionado a la explicabilidad.
Causalidad
Aunque si bien los sistemas dinámicos (y general las teorías de la complejidad) rompen con los modelos causalistas clásicos, aún queda por resolver si efectivamente estos sistemas dejan de ser causales o mantienen una causalidad compleja. Esto tendría consecuencias importantes para una ciencia del desarrollo, específicamente en la comprensión del desarrollo bajo un marco determinista o estocástico.
El movimiento de la complejidad, en general, se ha convertido en la esperanza de aquellos que buscan ver la realidad de manera menos determinada y más impredecible. El mundo del caos es comprendido como algo a lo cual no es posible acceder, lo que significa una posición de ruptura, por muchos bienvenida, frente a los paradigmas tradicionales en la ciencia, caracterizados por la predicción. Sin embargo, para entender este dilema, consideremos en principio, como lo hace la mayoría de investigadores en desarrollo, que el desarrollo en sí es un sistema abierto, en donde es posible el intercambio del individuo con el medio a lo largo de su ciclo vital. Según Erwin Schrödinger, físico austriaco, premio Nobel en 1933, y uno de los padres de la mecánica cuántica, un sistema abierto se alimenta de entropía negativa, y mientras un sistema tal sea capaz de seguir alimentándose de esta entropía, tenderá hacia estados de menor entropía positiva, de menor desorden y de mayor improbabilidad. Esto es realmente importante porque nos señala que en sistemas caóticos autoorganizables, donde existen bucles de retroalimentación o intercambios e interacciones constantes entre niveles organizativos, la probabilidad o estocasticidad desaparece, dando lugar a estados más determinísticos. Sin embargo, la discusión continúa abierta si se considera la existencia de un caos determinístico en el desarrollo1, ya que sería necesario hablar de una posible estocasticidad debido a la perdida de información a lo largo del tiempo, lo que mantiene intacta la discusión antes referida.
Explicabilidad
Otra de las controversias fuertes en la ciencia versa sobre las características descriptivas y explicativas de ciertos modelos, perspectivas o teorías. Hasta el momento no es claro si la perspectiva de los sistemas dinámicos puede ser usada como marco explicativo de los fenómenos del desarrollo. Algunas cuestiones similares en otros campos de la psicología han sido presentadas por autores como Baratgin & Politzer (2006), al hablar tanto de las características normativas como descriptivas en redes bayesianas; o en los interesantes desarrollos de Moliner y Gutermann (2004) en representaciones sociales, sobre lo descriptivo o explicativo de una representación social. En el terreno de las representaciones sociales, por ejemplo, las dos vertientes con las cuales se estudia los fenómenos sociales dinámicos (vertientes descriptivas y explicativas) llegan a aproximarse, hecho que resalta su relación con lo señalado por Baratgin y Politzer (2006) en cuanto a que toda aproximación científica a un fenómeno buscaría aproximar los criterios normativos a los descriptivos. Por ahora, los sistemas dinámicos presentan una aplicación más bien descriptiva al campo del desarrollo; sin embargo, no se descarta un acercamiento a la cualidad explicativa de ésta herramienta, si consideramos que la misma posee una serie de propiedades epistémicas y ónticas visibles en los estados y observables de un sistema que exhibe caos determinístico (Atmanspacher, 2000; Atmanspacher & Kronz, 1998).
Un problema que se desprende del anterior es el referido al uso de las series temporales en la investigación psicológica. Independientemente que se considere el fenómeno del desarrollo como continuo o discreto, y en su defecto se utilice la versión continua o discreta de los sistemas dinámicos, para algunos existiría un problema al aplicar esta teoría a los fenómenos psicológicos, ya sea porque generalmente se trata de problemas con series temporales relativamente cortas, con escalas de pocos intervalos, o por el posible alto nivel de ruido que se genera con las variables psicológicas, lo que imposibilita la construcción de modelos caóticos (Tscharcher & Scheier, 1998). El uso de series temporales implicaría, por un lado, la aplicación de métodos que permitan capturar muchos momentos en cortos intervalos de tiempo, como los utilizados en los estudios del microdesarrollo, y una preparación rigurosa en este tipo de matemática, que posibilite disminuir los niveles de ruido en la toma de datos, mientras se aproxime a un problema psicológico específico.
Como consecuencia de lo anterior surgen los siguientes inconvenientes en la integración de los sistemas dinámicos a la psicología del desarrollo:
Estipular las variables o condiciones iniciales que intervienen en la aparición de un proceso complejo llega a ser un proceso difícil para cualquier investigación en desarrollo. Esta dificultad puede ser problemática para la generación de modelos de series de tiempos necesarios para un análisis dinámico. Cuáles son las condiciones iniciales que determinan el desarrollo de un sistema, llega a ser una pregunta por solventar en cualquier investigación del desarrollo sujeta a este marco.
Por otro lado, para la psicología del desarrollo el tema de la irreversibilidad genera varias controversias, por un lado, en el efecto o relación con la psicología piagetiana, donde la irreversibilidad no sólo es posible sino que se considera como un proceso fundamental de las estructuras del pensamiento en desarrollo, y segundo, en las relaciones o diferencias con posturas teleológicas del desarrollo, como la propuesta por Demetriou y Raftopoulos (1999), donde existiría un desenvolvimiento errático pero altamente direccionado del mismo.
Además, a pesar de la propuesta multidimensional, los límites de los niveles siguen siendo en muchas ocasiones difusos. El paso de una jerarquía a otra parece dar saltos cualitativos difíciles de manejar por la teoría.
También es importante señalar, que la perspectiva de los sistemas dinámicos apunta a procesos y estructuras que pueden, muchas veces, mantenerse cohesionados en el tiempo, dependiendo de parámetros de control específicos, en atractores relativamente estables. Las investigaciones actuales se han centrado más en el aspecto de la variabilidad en el tiempo real pero hasta el momento pocas se aventuran a explicar la posible estabilidad de las estructuras en los tiempos del desarrollo (van Geert y Steenbeek, 2005a, 2005b).
A pesar de estos retos, para algunos investigadores, con la inclusión de los sistemas dinámicos se podría dar un gran salto hacia delante en la ciencia del desarrollo, salto análogo a la moderna síntesis de la genética molecular o a la selección natural en la biología evolutiva (Keating & Miller, 2000). Las teorías modernas en desarrollo han empezado a tomar caminos distintos a los tradicionales. Ejemplo de ello son las nuevas propuestas como la de Gärdenfors (2000), dirigidas a estipular los principios de una geometría del pensamiento, a través de una teoría de los espacios conceptuales construidos sobre estructuras geométricas basadas en un número de dimensiones cualitativas; o los acercamientos de los desarrollos de Prigogine al campo de los sistemas sociales, donde se rescata la posibilidad de pensar un orden individual inscrito en una dinámica temporal (Prigogine, 1976). La ciencia del desarrollo parece avanzar de la mano de una nueva conceptualización del espacio y del tiempo en psicología. Estas nuevas búsquedas de explicación de estructuras y procesos en el tiempo han permitido la inclusión de aproximaciones totalmente novedosas del devenir psicológico, aproximaciones que sin duda han comenzado a impactar en la forma como se comprende el desarrollo infantil y adulto, en cómo se entienden las interacciones que se generan con el medio, y en los cambios a nivel del organismo, de las redes cerebrales, de las acciones y las representaciones del mundo (Castro & Flórez, 2007). Una comprensión agrupada en un marco más holista, complejo y dinámico.
Notas
1El caos determinista se sustenta sobre las siguientes cuatro características: a. son entornos que presentan una gran sensibilidad a las condiciones iniciales, y existen retroalimentaciones; b. se pueden describir matemáticamente con ecuaciones diferenciales no lineales; c. son disipativas, es decir, requieren aportes externos de energía; y d. se pierde una pequeña parte de la información en cada una de las etapas del proceso, de forma que no es posible conocer las condiciones iniciales tras un tiempo.
Referencias
Abraham, F. D., & Gilgen, A. R. (Eds.). (1995). Chaos theory in psychology. Westport, CT: Praeger. [ Links ]
Atmanspacher, H. (2000). Ontic and espistemic descriptions of chaotic systems. In D. M. Dubois (Ed.), Computing Anticipatory Systems: CASYS'99 - Third International Conference (pp. 465-478). Berlin: Springer. [ Links ]
Atmanspacher, H., & Kronz, F. (1998). Many realisms. Acta Polytechnica Scandinavica, Ma-91, 31-43. [ Links ]
Baratgin, J., & Politzer, G. (2006). Is the mind bayesian? The case for agnosticism. Mind & Society, 5(1), 1-38. [ Links ]
Beer, R. D. (2000). Dynamical approaches to cognitive science. Trends in Cognitive Sciences, 4(3), 91-99. [ Links ]
Bernstein, N. (1967). Coordination and regulation of movements. New York: Pergamon Press.
Bertenthal, B. (1999). Variation and selection in the development of perception and action. In G. Savelsbergh, H. L. J. van der Maas & P. van Geert (Eds.), Non-linear developmental processes (Vol. 175, pp. 105-121). Amsterdam: Koninklijke Nederlandse Academie van Wetenschappen.
Camras, L. A., & Witherington, D. C. (2005). Dynamical systems approaches to emotional development. Developmental Review, 25, 328-350.
Castro, J. A., & Flórez, R. (2007). La emergencia del lenguaje y los sistemas dinámicos. Revista Colombiana de Psicología, 16, 185-202.
Cobb, L., & Ragade, R. K. (1978). Applications of catastrophe theory in the behavioral and life sciences. Behavioral Science, 23, 291-419.
de Weerth, C., & van Geert, P. (1999). Transitions and variability in infant behavior. In G. Savelsbergh, H. L. J. van der Maas & P. van Geert (Eds.), Non-linear developmental processes (Vol. 175, pp. 3-14). Amsterdam: Koninklijke Nederlandse Academie van Wetenschappen.
de Weerth, C., & van Geert, P. (2002). Changing patterns of infant behavior and mother-infant interaction: Intra- and interindividual variability. Infant Behavior & Development, 24, 347-371.
de Weerth, C., van Geert, P., & Hoijtink, H. (1999). Intraindividual variability in infant behavior. Developmental Psychology, 35(4), 1102-1112.
Demetriou, A., & Raftopoulos, A. (1999). Modeling the developing mind: From structure to change. Developmental Review, 19, 319-368.
Duncan, T. E., Duncan, S. C., Strycker, L. A., & Li, F. (1999). An introduction to latent variable growth curve modeling: Concepts, issues, and applications. Mahwah, N.J.: Erlbaum.
Fabian, T., & Stadler, M. (1991). A chaos theoretical approach to delinquent behavior in psychosocial stress situations. Gestalt Theory, 13, 98-106.
Fischer, K. W., & Dawson, T. L. (2002). A new kind of developmental science: Using models to integrate theory and research. Monographs of the Society for Research in Child Development, 67, 1-17.
Fischer, K. W., & Paré-Blagoev, J. (2000). From individual differences to dynamic pathways of development. Child Development, 71(4), 850-853.
Fogel, A. (1988). Cyclicity and stability in mother-infant face-to-face interaction: A comment on Cohn and Tronick (1988). Developmental Psychology, 24(3), 393-395.
Fogel, A. (1999). Systems, cycles, and developmental pathways. Human Development, 42, 213-216.
Fogel, A., & Thelen, E. (1987). Development of early expressive and communicative action: Reinterpreting the evidence from a dynamic systems perspective. Developmental Psychology, 23(6), 747-761.
Fogel, A., Toda, S., & Kawai, M. (1988). Mother-Infant face-to-face interaction in Japan and the United States: A laboratory comparison using 3-monthold infants. Developmental Psychology, 24(3), 398-406.
Freeman, W., & Skorda, C. (1990). Chaotic dynamics versus representationalism. Behavioral and Brain Sciences, 13, 167-168.
Gärdenfors, P. (2000). Conceptual spaces: The geometry of thought. Cambridge, MA: The MIT Press.
Gershkoff-Stowe, L., & Thelen, E. (2004). U-shaped changes in behavior: A dynamic systems perspective. Journal of Cognition and Development, 5(1), 11-36.
Granic, I., & Lamey, A. V. (2002). Combining dynamic systems and multivariate analyses to compare the mother-child interactions of externalizing subtypes. Journal of Abnormal Child Psychology, 30(3), 265-283.
Granott, N. (1998). A paradigm shift in the study of development. Human Development, 41, 360-365.
Granott, N., & Parziale, J. (Eds.). (2002). Microdevelopment: Transition processes in development and learning. New York, NY: Cambridge University Press.
Guastello, S. (2000). Nonlinear dynamics in Psychology. Discrete Dynamics in Nature and Society, 00, 1-20.
Haken, H. (1999). Synergetics and some applications to psychology. In W. Tschacher & P.-P. Daualder (Eds.), Dynamics, synergetics, autonomous agents. London: World Scientific.
Haken, H., Kelso, J. A. S., Fuchs, A., & Pandya, A. (1990). Dynamic pattern recognition of coordinated biological motion. Neural Networks, 3, 395-401.
Heiby, E. (1992). Some implications of chaos and multivariate theories for the assessment of depression. European Journal of Psychological Assessment, 8, 70.
Hofsten, C. v. (1989). Motor development as the development of systems: Comments on the special section. Developmental Psychology, 25(6), 950-953.
Howe, M. L., & Lewis, M. D. (2005). The importance of dynamic systems approaches for understanding development. Developmental Review, 25, 247-251.
Kamm, K., Thelen, E., & Jensen, J. L. (1990). A dynamical systems approach to motor development. Physical Therapy, 70(12), 763-775.
Kaplan, D. T. (2000). Structural equation modeling: Foundations and extensions. Thousand Oaks, C.A.: Sage.
Karmiloff-Smith, A. (1994). Más allá de la modularidad. Madrid: Alianza Editorial.
Keating, D. P., & Miller, F. K. (2000). The dynamics of emotional development: Models, metaphors, and method. In M. D. Lewis & I. Granic (Eds.), Emotion, development, and self-organization: Dynamic systems approaches to emotional development (pp. 373-392). Cambridge, U.K.: Cambridge University Press.
Kelso, J. A. S. (1981a). Contrasting perspectives on order and regulation in movement. In J. Long & A. Baddeley (Eds.), Attention and performance (IX). Hillsdale, N.J.: Erlbaum.
Kelso, J. A. S. (1981b). Motivating muscles: The problem of action. Contemporary Psychology, 26, 181-182.
Kelso, J. A. S., & Schöner, G. (1988a). Dynamic patterns of sensori-motor behavior: biological control structures and constraints. Neural Networks, 1.
Kelso, J. A. S., & Schöner, G. (1988b). Self-organization of coordinative movement patterns. Human Movement Science, 7, 27-46.
Kelso, J. A. S., & Tuller, B. (1984). A dynamical basis for action systems. In M. S. Gazzaniga (Ed.), Handbook of Neuroscience (pp. 321-356). New York: Plenum.
Klahr, D. (1992). Information-processing approaches to cognitive deve-lopment. In M. H. Bornstein & M. E. Lamb (Eds.), Developmental psychology: An advanced textbook (3rd ed., pp. 273-335). Hillsdale, NJ: Lawrence Erlbaum.
Kugler, P., Kelso, J. A. S., & Turvey, M. (1980). On the control and coordination of naturally developing systems. In J. A. S. Kelso & J. E. Clark (Eds.), The development of movement control and coordination (pp. 5-78). New York: John Wiley.
Lavelli, M., & Fogel, A. (2002). Developmental changes in mother-infant face-to-face communication: Birth to 3 months. Developmental Psychology, 38(2), 288-305.
Lavelli, M., & Fogel, A. (2005). Developmental changes in the relationship between the infant's attention and emotion during early face-to-face communication: The 2-month transition. Developmental Psychology, 41(1), 265-280.
Lewis, M. D. (2000a). Emotional self-organization at three time scales. In M. D. Lewis & I. Granic (Eds.), Emotion, development, and self-organization: Dynamic systems approaches to emotional development. Cambridge, U.K.: Cambridge University Press.
Lewis, M. D. (2000b). The promise of dynamic systems approaches for an integrated account of human development. Child Development, 71(1), 36-43.
Lewis, M. D. (2002). Interacting time scales in personality (and cognitive) development: Intentions, emotions, and emergent forms. In N. Granott & J. Parziale (Eds.), Microdevelopment: Transition processes in development and learning (pp. 183-212). New York, NY: Cambridge University Press.
Lewis, M. D. (2005). Bridging emotion theory and neurobiology through dynamic systems modeling. Behavioral and Brain Sciences, 28, 169-245.
Lewis, M. D., Lamey, A. V., & Douglas, L. (1999). A new dynamic systems method for the analysis of early socioemotional develop-ment. Developmental Science, 2(4), 457-475.
Li, W., & Xu, L. (1987). Chaos and its significance in physiological psychology. Acta Psychologica Sinica, 19, 307-311.
Lonie, I. (1991). Chaos theory: A new paradigm for psychotherapy? Australia and New Zealand Journal of Psychiatry, 25, 584.
Moliner, P., & Gutermann, M. (2004). Dynamique des descriptions et des explications dans une representation sociale. Textes sur les répresentations sociales, 13, 2.1-2.12.
Munakata, Y., & McClelland, J. L. (2003). Connectionist models of development. Developmental Science, 6(4), 413-429.
Nelson, A. (1992). The application of chaos theory to the understanding of psychological transformations. Dissertation Abstracts International, 52, 4477.
Piaget, J. (1969a). Biología y comportamiento. México: Siglo Veintiuno.
Piaget, J. (1969b). Psicología de la inteligencia. Buenos Aires: Psique. (Original publicado en 1947).
Piaget, J. (1971). El estructuralismo. Buenos Aires: Proteo.
Piaget, J. (1972). El nacimiento de la inteligencia en el niño. Madrid: Aguilar. (Original publicado en 1936).
Piaget, J., & Inhelder, B. (1973). Psicología del niño. Madrid: Morata.
Prigogine, I. (1973). Irreversibility as a symmetry-breaking process. Nature, 246, 67-71.
Prigogine, I. (1976). Order through fluctuation: Self-organization and social system. In E. Jantsch & C. Waddington (Eds.), Evolution and consciousness: Human systems in transition. Reading, MA: Addison-Wesley.
Robertson, R., & Combs, A. (Eds.). (1995). Chaos theory in Psychology and life sciences. Mahwah, NJ: Erlbaum.
Rose, S. P., & Fischer, K. W. (1998). Models and rulers in dynamical development. British Journal of Developmental Psychology, 16(1), 123-131.
Ruhland, R., & van Geert, P. (1998). Jumping into syntax: Transitions in the development of closed class words. British Journal of Developmental Psychology, 16, 65-95.
Samuelson, L. K., & Smith, L. B. (2000). Grounding development in cognitive process. Child Development, 71(1), 98-106.
Sawyer, R. K. (2002). Emergence in psychology: Lessons from the history of non-reductionist science. Human Development, 45, 2-28.
Scherer, K. R. (2000). Emotions as episodes of subsystem synchronization driven by nonlinear appraisal processes In M. D. Lewis & I. Granic (Eds.), Emotion, development, and self-organization: Dynamic systems approaches to emotional development. Cambridge, U.K.: Cambridge University Press.
Schmid-Denter, U. (1992). Chaos research: A new physical challenge for psychology? Psychologic Erziehung und Unterricht, 39, 1-16.
Schöner, G., & Kelso, J. A. S. (1988). Dynamic pattern generation in behavioral and neural systems. Science, 239, 1513-1520.
Schutte, A. R., Spencer, J. P., & Schöner, G. (2003). Testing the Dynamic Field Theory: Working memory for locations becomes more spatially precise over development. Child Development, 74(5), 1393-1417.
Siegler, R. (1994). Cognitive variability: A key to understanding cognitive development. Current Directions in Psychological Science, 3, 1-5.
Siegler, R. (1996). Emerging minds: The process of change in children's thinking. New York: Oxford University Press.
Skinner, H. (1989). Butterfly wings flapping: Do we need more "chaos" in understanding addiction? British Journal of Addiction, 84, 353-356.
Smith, L. B. (2005). Cognition as a dynamic system: Principles from embodiment. Developmental Review, 25, 278-298.
Smith, L. B., & Thelen, E. (2003). Development as a dynamic system. Trends in Cognitive Sciences, 7(8), 343-348.
Smith, L. B., & Thelen, E. (Eds.). (1993). A dynamic systems approach to development: Applications. Cambridge, MA: The MIT Press.
Spencer, J. P., & Schöner, G. (2003). Bridging the representational gap in the dynamic systems approach to development. Developmental Science, 6(4), 392-412.
Spencer, J. P., Smith, L. B., & Thelen, E. (2001). Tests of a dynamic systems account of the A-not-B error: The influence of prior experience on the spatial memory abilities of two-year-olds. Child Development, 72(5), 1327-1346.
Sporns, O., & Edelman, G. M. (1993). Solving Bernstein's problem: A proposal for the development of coordinated movement by selection. Child Development, 64, 960-981.
Steenbeek, H., & van Geert, P. (2005). A dynamic systems model of dyadic interaction during play of two children. European Journal of Developmental Psychology, 0(0), 1-41.
Sternberg, R. J. (1999). After Piaget, the Deluge. Human Development, 42, 220-224.
Sulis, W., & Combs, A. (Eds.). (1996). Nonlinear dynamics in human behavior. Singapur: World Scientific.
Thelen, E. (1984). Learning to walk: Ecological demands and phylogenetic constraints. In L. P. Lipsitt (Ed.), Advances in infancy research (Vol. 3, pp. 213-250). Norwood, NJ: Ablex.
Thelen, E. (1985). Developmental origins of motor coordination: Leg movements in human infants. Developmental Psychobiology, 18, 1-22.
Thelen, E. (1995). Motor development: A new synthesis. American Psychologist, 50(2), 79-95.
Thelen, E. (2000a). Grounded in the world: Developmental origins of the embodied mind. Infancy, 1(1), 3-28.
Thelen, E. (2000b). Motor development as foundation and future of developmental psychology. International Journal of Behavioral Development, 24(4), 385-397.
Thelen, E., & Bates, E. (2003). Connectionism and dynamic systems: Are they really different? Developmental Science, 6(4), 378-391.
Thelen, E., Kelso, J. A. S., & Fogel, A. (1987). Self-organizing systems and infant motor development. Developmental Review, 7, 39-65.
Thelen, E., Schöner, G., Scheier, C., & Smith, L. B. (2001). The dynamics of embodiment: A feld theory of infant perseverative reaching. Behavioral and Brain Sciences, 24, 1-86.
Thelen, E., & Smith, L. B. (1994). A dynamics systems approach to the development of cognition and action. Cambridge, MA: The MIT Press.
Thelen, E., & Ulrich, B. D. (1991). Hidden skills: A dynamic systems analysis of treadmill stepping during the first year. Monographs of the Society for Research in Child Development, 56(Serial No 223).
Thom, R. (1975). Structural stability and morphogenesis: An outline of a general theory models. New York: Benjamin.
Tscharcher, W., & Scheier, C. (1998). Complex psychological systems: Synergetics and chaos. In F. Masterprasqua & P. A. Perna (Eds.), The psychological meaning of chaos. Washington: American Psychological Association.
Turvey, M. (1990). Coordination. American Psychologist, 45, 938-953.
Valsiner, J. (2006). Developmental epistemology and implications for methodology. In R. Lerner (Ed.), Handbook of Child Psychology (6 ed., Vol. 1 Theoretical models of human development). New York: Wiley.
van der Maas, H. L. J., & Hopkins, B. (1998). Developmental transitions: So what's new? British Journal of Developmental Psychology, 16, 1-13.
van der Maas, H. L. J., & Molenaar, P. C. M. (1992a). A catastrophe-theoretical approach to cognitive development. Psychological Review, 99, 395-417.
van der Maas, H. L. J., & Molenaar, P. C. M. (1992b). Stagewise cognitive development: An application of catastrophe theory. Psychological Review, 99(3), 395-417.
van Dijk, M. (2004). Child language cuts capers: Variability and ambiguity in early child development. Groningen: University of Groningen.
van Geert, P. (1991). A dynamic systems model of cognitive and language growth. Psychological Review, 98, 3-53.
van Geert, P. (1994). Dynamic systems of development: Change between complexity and chaos. London: Harvester Wheatsheaf.
van Geert, P. (1998). A dynamic systems model of basic developmental mechanisms: Piaget, Vygotsky, and beyond. Psychological Review, 105(4), 634-677.
van Geert, P. (2000). The dynamics of general developmental mechanisms: From Piaget and Vygotsky to dynamic systems models. Crrent Directions in Psychological Science, 9(2), 64-68.
van Geert, P. (2003). Dynamic systems approaches and modeling of developmental processes. In J. Valsiner & K. J. Conolly (Eds.), Handbook of Developmental Psychology (pp. 640-672). London: Sage.
van Geert, P., & Steenbeek, H. (2005a). A complexity and dynamic systems approach to developmental assessment, modeling and research. In K. W. Fischer, A. Battro & P. Lena (Eds.), Mind, brain and education. Cambridge, UK: Cambridge University Press.
van Geert, P., & Steenbeek, H. (2005b). Explaining after by before: Basic aspects of a dynamic systems approach to the study of development. Developmental Review, 25, 408-442.
van Geert, P., & van Dijk, M. (2002). Focus on Variability: New tools to study intra-individual variability in developmental data. Infant Behavior and Development, 25(4), 340-374.
Vroon, P. (1992). Chaos theory and human behavior. Psychology, 27, 2-7.
Vygotski, L. S. (1989). El desarrollo de los procesos psicológicos superiores. Barcelona: Crítica.
Yan, Z., & Fischer, K. W. (2002). Always under construction: Dynamic variations in adult cognitive microdevelopment. Human Development, 45(3), 141-160.
Zanone, P. G., & Kelso, J. A. S. (1991). Experimental studies of behavioral attractors and their evolution with learning. In J. Requin & G. E. Stelmach (Eds.), Tutorials in motor neuroscience (pp. 121-133). Dordrecht: Kluwer.