ANÁLISIS DEL COMPORTAMIENTO NO-LINEAL Y CAOS EN UNA MICROCAVIDAD SEMICONDUCTORA

ANALYSIS OF NON-LINEAR BEHAVIOR AND CHAOS IN A SEMICONDUCTING MICROCAVITY

Andrés F. Urquijo-Rodriguez, José D. Hernández-Rivero, Herbert Vinck-Posada

Grupo de Óptica e información cuántica, Departamento de Física, Universidad Nacional de Colombia, Bogotá, Colombia.
Andrés F. Urquijo-Rodriguez: afurquijor@unal.edu.co

(Recibido: Febrero/2016. Aceptado: Mayo/2016)

Resumen

En este trabajo presentamos un estudio del régimen no lineal para una microcavidad semiconductora que contiene un punto cuántico. Nosotros caracterizamos el régimen no lineal de este sistema a través de la dinámica de los valores esperados de operadores usando la aproximación de campo medio en la imagen de Heisenberg. También presentamos cuantificadores clásicos de caos tales como: exponentes de Lyapunov, secciones de Poincaré y diagramas de bifurcación en este sistema.

Palabras clave: Caos, microcavidad, punto cuántico, Exponente de Lyapunov.

Abstract

In this work we present a study on the nonlinear behavior of a semiconducting microcavity containing a single Quantum-Dot. We characterize the nonlinear regime of this system through the dynamics of mean values of operators by using the mean field approximation in the Heisenberg picture. We also present classical quantifiers of chaos such as: Lyapunov exponents, Poincare sections and bifurcation diagrams in this system.

Keywords: Chaos, Lyapunov exponents, Quantum Dot, Microcavity.

Introducción

En las últimas décadas, el estudio de las propiedades ópticas de sistemas semiconductores, por medio de la dinámica no lineal se ha convertido en un creciente campo de estudio en la Física tanto teórica como experimental, gracias a la aplicabilidad de estos sistemas en el campo de los dispositivos opto-electrónicos. El acoplamiento entre la luz y la materia en sistemas semiconductores como los puntos cuánticos, genera efectos cuánticos y no-linealidades en el sistema, como el cambio de las propiedades cuántico-estadísticas de la la luz emitida, y fenómenos de biestabilidad [1] y multiestabilidad. Esto hace, de la teoría de los sistemas dinámicos una herramienta esencial, para la descripción de este tipo de fenómenos, puesto que estrategias como el formalismo de la ecuación maestra, no permiten dilucidar estos efectos, debido al carácter lineal de la teoría.

En sistemas reales, tales como los utilizados en el laboratorio, la presencia continua de entes forzantes, como el ruido electromagnético, generan efectos considerables sobre la mediciáon de este tipo sistemas. Ejemplos de tales resultados obtenidos por medio de perturbaciones externas incluyen: control del caos, resonancia estocástica [2, 3], dinámica caótica extraña, entre otras. Esto nos lleva a explorar como la dináamica de estos sistemas depende de su espacio de paráametros en regámenes no lineales.

Modelo Teórico

Nosotros estudiamos un punto cuántico ubicado dentro de una microcavidad semiconductora (Fig. 1). Este se encuentra localizado en la posición donde el campo electromagnético es máximo dentro de la microcavidad. Nuestro sistema se encuentra inicialmente en el estado base y evoluciona hasta encontrar el estado estacionario. Para describir la evolución temporal de este sistema, consideramos el hamiltoniano de Jaynes-Cumming [4]:

En este, los dos primeros términos corresponden a la energía propia de la microcavidad y la energía propia del excitón, y el último término representa la interacción entre la cavidad y el punto cuántico.

En la búsqueda de regiones del espacio de parámetros del sistema en donde se exhiba el comportamiento no lineal, consideramos un bombeo coherente producido por un campo eléctrico externo [5], actuando como un ente forzante. Este término es incluido en el sistema de forma clásica como una estrategia para estudiar la dependencia del sistema a fluctuaciones periódicas en el tiempo. Matemáticamente este bombeo lo escribimos como

Donde f es el parámetro de amplitud del campo y O su frecuencia de oscilación.

En la aproximación de campo medio, se considera que dos operadores poseen mínima correlación

Es decir, que el valor esperado de un producto de operadores puede ser factorizado como el producto de sus valores esperados. Usando este hecho, en la imagen de Heisenberg podemos escribir la evoluciún temporal de los valores esperados de los operadores a, a^† y σ y σ^† de nuestro sistema por medio del siguiente sistema dinámico no-autónomo [6]:

Donde τ es un tiempo adimensional normalizado como: τ = t/τ_c. γ y k son los canales de disipación adimensionales agregados de forma fenomenologica al sistema del exciton y de los fotones en la cavidad

y g es la constante de interacción entre la cavidad y el punto-cuántico.

Para obtener el sistema de ecuaciones diferenciales que rigen la dinámica del sistema físico en la aproximación de campo medio, es necesario tener especial cuidado con la estadística que siguen las partículas involucradas en el sistema, para obtener una correcta descripción física del problema. En nuestro caso los fotones y los excitones siguen las estadísticas bosónicas y termiónicas, respectivamente:

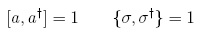
Para integrar numéricamente el sistema de ecuaciones [2], separamos la parte real e imaginaria de este sistema, obteniendo un conjunto de ecuaciones diferenciales ordinarias acopladas con valores reales:

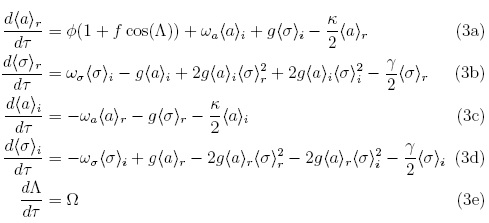
Con la restricción ⊥ = Ωτ.

Debido a la alta dimensionalidad que posee el sistema dinámico, y el hecho de ser no-autónomo, es complejo realizar un análisis de tipo analítico. Así, una estrategia más sencilla para abordar el problema es el uso de técnicas numéricas.

En la Integración numérica de este sistema utilizamos el método Runge-Kutta de orden cuatro con un tamaño de paso temporal Δt = 2π/5000. Aplicando este método en su versión para sistemas acoplados encontramos la evolución temporal de las partes real e imaginaria de los valores medios de los operadores α y σ. Una vez integradas las ecuaciones que describen la dinámica de los valores medios, construimos nuestro espacio de fase con las intensidades I_a e I_σ, definidas como:

Estas intensidades son respectivamente el número medio de excitones y el número medio de fotones en la cavidad.

Exponentes de Lyapunov

Una de las características importantes presentes en un sistema dinámico caótico, es la denominada sensibilidad a las condiciones iniciales. En donde órbitas que evolucionan desde una vecindad del espacio de fase se separan exponencialmente rápido luego de un tiempo característico llamado tiempo horizontal.

Matemáticamente este hecho se expresa como [7, 8]:

Donde δ₀ es la separación infinitesimal inicial entre dos orbitas x* y x^†, δ_n es la separación existente entre las dos órbitas luego de haber transcurrido un tiempo t = nΔt, y λ es el mayor exponente de Lyapunov.

Cuando el sistema de interés es un flujo (sistema de ecuaciones diferenciales) en el espacio de fase, es importante conocer como es el crecimiento exponencial en cada una de las direcciones principales del sistema, por lo cual existe un exponente de Lyapunov asociado a cada dirección principal. A este conjunto de cantidades se le conoce como espectro de Lyapunov y tiene como característica que dichas cantidades están ordenadas.

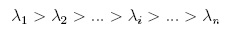
Resultados y discusión

En nuestro análisis consideramos la dependencia que tiene el comportamiento dinámico del sistema en función del parámetro de amplitud del campo ƒ. Asó, definimos el restante espacio de parámetros fijo de la siguiente manera: Ω = 1.01eV, Φ = 0.695eV, g = 0.1965eV, k = 0.07eV, γ = 0.009eV, ω_σ = 1.0eV, y ω_σ = 1.1eV

Periodicidad

El primer caso a considerar es la denominada región periódica. La figura 3 muestra la evolución temporal de las intensidades I_a e I_σ, también se muestran el mayor y el menor exponente de Lyapunov. Dado que ambos exponentes de Lyapunov son negativos, en esta región del espacio de parámetros la solución del sistema tiene comportamiento periódico, esto también lo confirma la respectiva sección de Poincaré, figura 4. En esta, se muestra el cruce del flujo en el espacio de fase a través de un plano ubicado en ℜ{a} = 0, dicho cruce presenta una conglomeración de puntos en dos regiones muy pequeñas de la sección, lo que indica la existencia de una órbita de período 2.

Cuasi-periodicidad

Otro de los regímenes observados en el sistema, es el cuasi-periódico. En este la solución es una mezcla de movimientos periódicos de muchas frecuencias fundamentales diferentes. El comportamiento del sistema físico en esta región es mostrado en la figura 5. El mayor exponente de Lyapunov en esta región ƒ Є [0.0, 0.293)) es cero, lo que indica que en una de las direcciones principales del sistema no se presenta convergencia ni divergencia exponencial en la evolución temporal. La sección de Poincare en la región cuasi-periódica es mostrada en la figura 6.

Caos

La última región a discutir es la caótica. Nuestros experimentos numéricos nos llevaron a encontrar una región donde los exponentes de Lyapunov (mayor y menor) poseen respectivamente valores positivos y negativos, lo cual implica que existe divergencia entre orbitas vecinas del espacio de fase. La región del espacio de parámetros en donde ocurre tal comportamiento es ƒ Є [0.294, 0.304]. La evolución temporal del sistema es mostrada en la figura 7.

La sección de Poincare en este régimen sufre múltiples cruces, lo cual resulta en una región dispersa sobre el espacio de fase del sistema (Fig. 9). La evolución del sistema carece de una periodicidad y un estado estacionario definido. Para finalmente obtener información completa del espacio de parámetros del sistema y completar los requisitos para catalogar el sistema como caótico, mostramos el diagrama de bifurcaciones del sistema (Fig. 10). En donde vemos que existe una dependencia de la dinámica del sistema a cambios sobre el espacio de parámetros. La ruta al caos en este sistema no es la usual, es decir, no se presenta como una cascada de doblamiento de período, sino inicia con un régimen cuasi-periódico, luego caótico y al final una solución periódica.

Conclusiones

Analizamos los distintos tipos de comportamiento dinámico presentes en el sistema de un punto cuántico dentro de una microcavidad semiconductora, modelado a través del hamiltoniano de Jaynes-Cummings bajo la acción de un forzamiento externo y rangos de disipación, usando la aproximación de campo medio y la teoría de los sistemas dinámicos. Encontramos una región del espacio de parámetros del sistema en donde la dinámica es caótica. Además, mostramos que existe dependencia de la dinámica al espacio de parámetros del sistema. Otros comportamientos como periodicidad y cuasi-periodicidad, también se encuentran en este sistema.

Agradecimientos

Este trabajo ha sido financiado por Colciencias dentro del proyecto con código 110156933525, contrato número 026-2013 y código HERMES 17432. Por otra parte, reconocemos el apoyo técnico y computacional del Grupo de (Óptica e Información Cuántica de la Universidad Nacional de Colombia, Sede Bogotá.

Referencias

[1] A. Baas, J. P. Karr, H. Eleuch, and E. Giacobino, Phys. Rev. A 69, 023809 (2004).         [ Links ]

[2] R. Benzi, A. Sutera, and A. Vulpiani, Journal of Physics A: Mathematical and General 14, L453 (1981).         [ Links ]

[3] C. Rouvas-Nicolis and G. Nicolis, Scholarpedia 2, 1474 (2007).         [ Links ]

[4] J. I. Perea, D. Porras, and C. Tejedor, Phys. Rev. B 70, 115304 (2004).         [ Links ]

[5] H. Eleuch and A. Prasad, Physics Letters A 376, 1970 (2012).         [ Links ]

[6] Prants and Konkov, Microcavities and Photonics Bandgaps: Dynamical chaos for the strongly coupled microcavity-quantum well-exciton system (Springer, 1996) pp. 589-594.         [ Links ]

[7] E. Ott, Chaos in dynamical systems (Cambridge University Press, 1988).         [ Links ]

[8] M. Tabor, Chaos and integrability in nonlinear dynamics: An introduction (Wiley, 1993).         [ Links ]