INTUICIÓN, SESGOS y HEURÍSTICAS EN LA ELECCIÓN

Juan Santiago*

Freddy Cante

Juan Santiago es Magister(c) en Ingenieria financiera. Magister en Educación, Pontificia Universidad Javeriana. Estudiante del Doctorado en Ciencias Económicas, Universidad Nacional de Colombia. Se desempeña actualmente como profesor de probabilidad, inferencia y modelos de análisis estadísticos en la Facultad de Ingeniería de la Pontificia Universidad Javeriana (Bogotá, Colombia). E-mail: jsantiago@javeriana.edu.co. Dirección de correspondencia: Cra 30 No 45-03, Universidad Nacional de Colombia, Doctorado en Ciencias Económicas, edificio 238, oficina 122 (Bogotá, Colombia).

Freddy Cante es Doctor en Ciencias Económicas de la Universidad Nacional de Colombia. Profesor e investigador del CEPI y de la Facultad de Ciencia Política y Gobierno de la Universidad del Rosario (Bogotá, Colombia). E-rnail: fredy.cantema@urosario.edu.co. Dirección de correspondencia: Calle 14 No 6-25. Universidad del Rosario, Facultad de Ciencia Política y Gobierno, CEPI (Bogotá, Colombia). En el presente artículo se expone una parte de las ideas desarrolladas por los autores en sus trabajos de grado (Mención Honorífica) y de Doctorado, respectivamente.

Este artículo fue recibido el 16 de mayo de 2008 y su publicación aprobada el 30 de septiembre de 2008.

Resumen

El Programa de investigación “Heurísticas y Sesgos” liderado por el economista Amos Tversky (fallecido en 1996) y por el sicólogo ganador del premio Nobel Daniel Kahneman, ha ofrecido desde 1971 una alternativa al Modelo de la Utilidad Esperada en el campo de la toma de decisiones. Las proposiciones de la “Teoría de Prospectos” enfocada en los aspectos psicológicos que afectan la elección individual, cuestionan el status normativo de la Teoría de la Elección Racional, sus supuestos y su pretensión predictiva. El presente artículo espera ofrecer al lector un contraste entre las dos teorías.

Palabras clave: elección, racionalidad, prospectos, incertidumbre, utilidad. JEL: D03, D11, D81.

Abstract

The “Heuristics and Biases” research program led by economist A. Tversky (who died in 1996) and by the Nobel Prize winning psychologist D. Kahneman, has provided since 1971 an alternative approach to the Expected Utility Model in the field of decision making. Assertions of this descriptive theory focused on the psychological aspects affecting individual choice, called “The Prospect Theory”, question the normative status of Rational Choice Theory, its underlying assumptions and it predictive pretension. This article aims to provide a contrast between the two theories.

Key words: choice, rationality, prospects, uncertainty, utility. JEL: D03, D11, D81.

Résumé

Le Programme de recherche “Heuristiques et Biais” animé par l’économiste Amos Tversky (décédé en 1996) et par le psychologue gagnant du prix Nobel Daniel Kahneman, a offert dès 1971 une alternative au Modèle de l’Utilité Espérée dans le domaine de la théorie du choix. Les propositions de la “Théorie de Prospectus” orientée vers les aspects psychologiques qui affectent l’élection individuelle, défie le statut normatif de la Théorie du choix Rationnel, ses suppositions et sa prétention prédictive. Cet article cherche à offrir au lecteur une comparaison entre les deux théories.

Mot clés: théorie du choix, rationalité, prospectus, incertitude, utilité. JEL : D03, D11, D81.

"Cierta clase de optimismo, o de supuesto optimismo, afirma que si nos esforzamos pensando, o si somos lo suficientemente racionales, podemos resolver todos nuestros problemas".

H. A. Simon

"En la medida en que se refieren a la realidad las proposiciones matemáticas no son ciertas, yen la medida en que son ciertas no se refieren a la realidad".

Albert Einstein

El siglo pasado dejó a su paso importantes desarrollos de la teoría económica, entre los que se destacan la teoría de la elección racional y el modelo de la utilidad esperada; sin embargo, tales herencias intelectuales parecen quedar confinadas al mundo de lo ideal. Pese a que tal empresa intelectual navega en contravía de la realidad, aún arrancando el siglo XXI persiste la obsesión de cientos de economistas y científicos sociales por esta tentativa y el, quizás, excesivo uso de las matemáticas para enfrentarse a realidades profundamente inestables e inciertas. Posiblemente, en un mañana, las secciones de cuentos de ficción de las bibliotecas contengan cientos de libros con aplicaciones de elección racional y modelos de utilidad esperada, para un vasto conjunto de temas que van desde dietas de un consumidor, pronósticos de una empresa, hasta procesos más complicados como la acción colectiva, el cambio social y el conflicto internacional. La racionalidad, en el sentido estrecho que la define la Teoría de la Elección Racional, no puede explicar todos los fenómenos que se le pide que explique.

A pesar de la existencia de potentes equipos computacionales para el procesamiento de la inmensa cantidad de información disponible, la toma de decisiones, al menos para la inmensa mayoría de las personas, no dista mucho de los burdos procesos de escogencia de cinco siglos atrás. Los problemas de sesgos, prejuicios, explosiones emocionales y miopía presentes en las escogencias de los personajes de una comedia de William Shakespeare, como El Mercader de Venecia, aún son moneda corriente en las decisiones de comienzos del tercer milenio. Una posible ventaja en nuestros días es que algunos científicos sociales comienzan a mostrar, mediante argumentos críticos, persistente observación y experimentación, las viejas evidencias que, mediante un lenguaje más emotivo, habían mostrado notables literatos. Aquí se destacan los seminales escritos de Hayek sobre complejidad e incertidumbre (1978), de Hirschman en relación con los valores o metapreferencias y el amor cívico (1984) y de Elster acerca de las emociones (1999).

Apreciaciones buenas o no, con mucho fundamento o muy poco, han intentado cuestionar los supuestos de la racionalidad perfecta y el modelo de la utilidad esperada. Objeciones tempranas al modelo en cuestión vinieron de Allais (1954, 2003), que presentó un contraejemplo a la Escuela Americana (liderada por Samuelson y Savage) en el cual surgía una reversión de preferencias por parte de un agente confrontado ante dos formas lógicamente equivalentes de descripción del problema de elección.

Simon (1989, original de 1954, 2006) entabló una crítica fundamental a la idea de racionalidad perfecta que consideró inalcanzable para el ser humano en virtud de las limitaciones cognitivas que lo aquejan, mostró con argumentos y evidencias empíricas que, es más realista hablar de una racionalidad limitada pues las personas tan sólo pueden alcanzar soluciones satisfacientes (suficientemente satisfactorias) y no óptimos. Otras implicaciones derivadas del seminal aporte de Simon se resumen a continuación:

Dadas las limitaciones cognitivas de los agentes en el proceso de elección observadas por Simon, en línea con Hayek (1978), la economía del conocimiento de las complejas sociedades extensas funciona con individuos que conocen muy poco. Es decir, las decisiones individuales y colectivas sensatas, en contravía de los supuestos de perfecta información, muestran que las personas deciden con poca información seleccionada aunque cuenten con mucha informacion disponible, dada su limitada capacidad de procesamiento de información (algo también señalado por Simon).

Quizás la contribución más valiosa de la teoría de juegos ha sido la de mostrar cuan indefinible es la racionalidad cuando los jugadores poseen ilimitadas capacidades computacionales para anticipar las expectativas de los demás.

Gran parte de las decisiones humanas, en particular las de la gente con más experiencia en la ciencia y el arte, son producto de la intuición (escogencia automática), y no de prolongados y sofisticados procesos de elección racional. Los agentes no optimizan.

El mundo de lo artificial, que abarca el ámbito de lo económico, es contingente y no puede ser objeto más que de unos ejercicios de predicción muy generales, sin aventurarse en detallar escenarios futuros, sin usar cifras y sin olvidar la enorme cantidad de soluciones creativas y diversas que pueden surgir.

Por su parte, Strotz (1955) enfatizó en la inconsistencia de las preferencias a lo largo del tiempo. En Loewenstein y Elster (1992) se ofrece un análisis de las implicaciones del trabajo de Strotz, referido en particular, al hedonismo ya la valoración intertemporal. Edwards (1961) propuso reemplazar las probabilidades canónicas que multiplicaban a las utilidades esperadas dentro del esquema de la Utilidad Esperada por funciones de ponderación dependientes de esas probabilidades.

Dentro de la Teoría de la Utilidad Esperada, un problema persistente ha sido la noción de la utilidad y la posibilidad de su medición, problema soslayado asumiendo la imposibilidad de una medición "objetiva" para un fenómeno "subjetivo". Contrario a la usanza de una función de utilidad evaluada sobre estados finales de riqueza, Markowitz (1952) propuso una función de utilidad relativa al consumo corriente que, años mas tarde, fue evaluada por Mosteller y Nogee (1961, en Edwards 1961) Y por Suppes (1961), dando como resultado una utilidad con dos regiones una convexa y otra cóncava divididas por un punto de inflexión.

Las observaciones precedentes, ya fuera de manera implícita o explícita, buscaron salvar el modelo de la utilidad esperada de dos maneras, primero, defendiendo sus pi lares (probabilidades bayesianas y la existencia del una función de utilidad) y segundo, intentando' cerrar la brecha entre sus prescripciones y los resultados observados en la realidad.

En los años setentas del siglo XX, Kahneman y Tversky (1979) comenzaron a desarrollar una serie de experimentos para analizar la toma de decisiones bajo riesgo e incertidumbre, algunos de sus resultados serán descritos a lo largo de este artículo. Bajo el nombre de Prospect theory -teoría de prospectos¹ o de la elección riesgosa-, tales autores incorporan, al menos, dos hallazgos fundamentales en la conducta del agente que decide: primero, su aversión a perder y, segundo, su ponderación de probabilidades. No serán objeto del presente escrito otras importantes teorías de la decisión como la Dissapointment theory² de Loomes y Sugden (1986) y Bell (1985) y la teoría de la utilidad esperada generalizada de Machina (1982) así como la de Procedural utility³ de Le Menestrel (2001).

Posterior a esta introducción sigue una síntesis del modelo de la utilidad esperada (sección 2); enseguida una presentación de la teoría sugerida por Kahneman y Tversky (sección 3); posteriormente se enuncian algunos problemas que no pueden ser resueltos mediante el modelo tradicional de la utilidad (sección 4) y, finalmente (sección 5); las conclusiones que alientan la indagación y la observación empírica en el ámbito de las ciencias sociales.

UNA SÍNTESIS DEL MODELO DE LA UTILIDAD ESPERADA

De forma contundente, Von Neumann y Morgenstern (1944, 30) señalaron que una tarea prioritaria de la teoría económica es la de ofrecer una adecuada descripción acerca de los supuestos que se han hecho sobre las motivaciones de los individuos. Ellos, sin embargo, siguieron la tradición de asumir que las personas se pueden clasificar en consumidores (maximizadores de satisfacción) y empresarios (maximizadores de beneficios), y subrayaron que los individuos racionales buscan las máximas utilidades. Además supusieron que los sujetos económicos tienen completa información sobre las características físicas de la situación en que operan y son capaces de realizar todas las operaciones matemáticas que el procesamiento de tal información requiere.

Los teóricos de la racionalidad perfecta asumen que los individuos tienen una consistencia lógica entre medios y fines y, por tanto, suponen la posibilidad de optimizar en el momento que el agente decide y a medida que pasa el tiempo. También asumen la existencia de un ordenamiento de las preferencias (las cuales se toman como dadas e invariables), sobre el cual el agente pueda maximizar la utilidad derivada de los resultados de sus decisiones, sea en un contexto de certeza, en uno riesgoso o en uno incierto. Uno de los productos de la teoría económica, compatible con la idea de una racionalidad perfecta, es el Modelo de Utilidad Esperada expuesto en textos como los de Von Neuman y Morgenstern (1944) y Savage (1954).

De acuerdo con Simon (1989, 23), son cuatro los supuestos del modelo de utilidad esperada:

1) Quien toma las decisiones tiene una bien definida función de utilidad (la cual envuelve la diversidad de valores humanos) y puede asignar un número cardinal que expresa la intensidad de su preferencia por un conjunto de sucesos futuros.

2) Las alternativas a elegir están bien definidas, y abarcan el presente y el futuro.

3) El elector conoce bien las consecuencias de cada alternativa (o estrategia), a tal punto que puede asignar una distribución de probabilidad conjunta a todas las series de hechos futuros.

4) Quien elige escogerá la opción o estrategia que maximice el valor esperado de su propia función de utilidad.

Simon (1989) sostiene que la teoría de la elección racional es un doble fraude y un instrumento mercenario. El doble timo de tal teoría se produce porque omite tratar el problema de las creencias (no reconoce que unos mismos hechos pueden ser interpretados de manera distinta por personas diferentes) y, además, evita considerar la diversidad de valores (no reconoce que las personas tienen fines diversos distintos a la maximización de la utilidad). En consecuencia, tal teoría, en el mejor de los casos (es decir, que funcionara en realidad), ayudaría a responder cómo decidir y, por tanto, estaría al servicio de seres con finalidades y valores tan disímiles como Hitler y Gandhi.

Por su parte Elster (1999) sostiene que las variadas motivaciones humanas (que subyacen a las preferencias) se podrían clasificar en tres subconjuntos, a saber: interés, entendido como la búsqueda de ventajas por parte de individuos o colectivos selectivos en forma de dinero, poder y estatus, y que es objeto de un cálculo racional; pasión que suele estar por fuera del control (por lo visceral) y que conduce directamente a la acción, y que abarca desde crudas reacciones (miedo, rabia, hambre, etc.) hasta emociones con referentes cognitivos (amor, odio, venganza, etc.); y razón, que podría ofrecer alguna referencia sobre valores deseables y sobre creencias verdaderas, pero que en un sentido práctico se reduce a un referente por lo imparcial. Y este autor (Elster 2002, 25) ofrece una aclaración conceptual sobre racionalidad y teoría de la utilidad esperada, que se esboza así:

[...] una acción es racional si cumple con estas tres condiciones de optimización. Primero, debe ser la mejor forma de satisfacer el deseo del agente, de acuerdo con sus creencias sobre las opciones disponibles y sus consecuencias. En los modelos económicos, esto se expresa diciendo que el agente maximiza la utilidad esperada [...] Segundo, las creencias deben ser las mejores que pueda formarse el agente, por ejemplo, tener la mayor probabilidad de ser verdad, dada la información disponible [...] Tercero, la cantidad de información que posee el agente debe ser el resultado de una inversión óptima en la adquisición de información [...]

No obstante, en ese mismo documento, Elster hace un recuento de diversos trabajos en los cuales se muestra que, con gran frecuencia, las preferencias de las personas son distantes de la verdad, y sus escogencias no sólo difieren de la optimalidad sino también de la racionalidad. Elster (1982) había hecho énfasis en que una teoría amplia de la racionalidad debería tener creencias cercanas a lo verdadero y deseos o preferencias no cuestionables éticamente (como la envidia y la venganza).

Los prospectos en la teoría de la utilidad esperada

Harsanyi (1989) formaliza la Teoría de la Utilidad en contextos ciertos, riesgosos e inciertos, teniendo en cuenta el comportamiento racional de un agente aislado. En el caso de elección individual bajo certidumbre, donde se utiliza una noción ordinal de utilidad, como lo aclara Varian (1992, 1994), el resultado de cualquier acción posible es plenamente predecible. En el caso de riesgo, la probabilidad de cualquier posible resultado es conocida, es decir se refiere a eventos "canónicos". En el caso de incertidumbre, algunas o todas las probabilidades objetivas son desconocidas o indefinidas para el agente. Para describir los resultados esperados de cualquier acción humana bajo certidumbre, se introduce la noción de prospectos seguros; bajo riesgo, la de prospectos riesgosos y bajo incertidumbre, la de prospectos inciertos. Enseguida se presentan los detalles de tal formalización.

Prospectos seguros y prospectos riesgosos

Se habla de riesgo o de incertidumbre cuando al menos alguna de las acciones disponibles para el agente puede tener dos o más resultados alternativos, sin que este sea capaz de discernir, cuál resultado particular ocurrirá en un caso dado. Específicamente, se habla de riesgo, cuando las probabilidades objetivas asociadas con todos los posibles resultados son conocidas por el agente.

Un prospecto seguro se caracteriza por especificar los valores de un número finito de variables (un vector con un número finito de componentes). El conjunto de todos los prospectos seguros será denotado por X.

Un prospecto riesgoso es una distribución de probabilidades sobre el conjunto X de todos los prospectos seguros. Si el número de diferentes prospectos seguros es finito, el prospecto riesgoso tendrá la siguiente notación:

[1]

Las p_i son mutuamente excluyentes, (2) y colectivamente exhaustivas (3):

[2]

[3]

Los prospectos riesgosos simples tienen como componentes a prospectos seguros; los prospectos riesgosos compuestos tienen como elementos (o al menos a algunos de ellos) a prospectos riesgosos o ciertos. El conjunto de todos los prospectos riesgosos, tanto simples como compuestos es Y. Cuando k = 2, esto es, para prospectos binarios, se usa la notación:

[4]

Las convenciones para los prospectos riesgosos se formalizan así:

1. Probabilidad unitaria: si p= 1 entonces:

[5]

Esto significa que un prospecto riesgoso que rinde el resultado A con probabilidad de 1 y por ende un resultado alternativo B con probabilidad O, es lo mismo que la plena certeza de obtener A.

Es claro que los prospectos seguros son casos especiales de los prospectos riesgosos; esto implica que X está contenido en Y.

2. Conmutatividad:

[6]

3. Adición de probabilidades. Sean A_l = A₂ entonces:

[7]

Si dos eventos disyuntos tienen el mismo pago podemos sumar sus probabilidades por la ley de adición de probabilidades.

4. Multiplicación de probabilidades (principio de loterías de dos etapas). Sean los prospectos:

[8]

[9]

Entonces:

[10]

Donde E es una lotería de dos etapas. En la etapa 1 el poseedor de un billete E tendrá una probabilidad q de ganar el tiquete C, y tendrá la probabilidad (1 - q) de ganar el premio D. Si gana C, participa en la etapa dos de la lotería, donde tiene la probabilidad p de ganar el premio A y la probabilidad 1 - p de ganar el premio B. Luego, por la ley de multiplicación de probabilidades, asumiendo que los resultados de las etapas son estadísticamente independientes entre sí, se obtendrá una probabilidad pq de ganar A, una probabilidad (1 - p)q de ganar B y una probabilidad (1 - q) de ganar D. La convención 4 supone que el tomador de decisiones será indiferente entre una lotería de una etapa y una de dos etapas.

Prospectos inciertos

En este caso, si el tomador de decisiones toma alguna decisión particular, en general puede predecir que esta acción producirá uno o más resultados alternativos, A_l, A₂, ... , A_k. donde las probabilidades objetivas asociadas con estos resultados alternativos no son conocidas. Será usado el prospecto incierto

[11]

Esto indica que bajo el prospecto incierto B, el resultado A_i será obtenido si el evento e_i, ocurre. Es claro que los eventos e_k son mutuamente excluyentes y colectivamente exhaustivos y "deben ser elegidos de tal forma que uno y sólo uno de ellos ocurra en cualquier caso dado", enfatizó Harsanyi. Con k = 2, se tiene:

[12]

Donde e* es la no ocurrencia del condicionante e, que recibe el nombre de "evento complementario de e". El conjunto de prospectos inciertos es Z. Las convenciones para los prospectos inciertos se formalizan así:

l. Plena certeza:

[13]

Según esta convención, cualquier evento cierto puede ser escrito como incierto. Así los prospectos seguros serán casos particulares de los prospectos inciertos.

Por tanto X está contenido en Z y como A también puede ser un prospecto riesgoso, Y está contenido en Z.

2. Conmutatividad:

[14]

Maximización de la utilidad en el caso de certidumbre

Aquí se usarán los conceptos de preferencia o de indiferencia. A es preferido a B por parte del agente, si él siempre (es decir, con probabilidad igual al), elige A en vez de B, dondequiera que tenga que elegir entre ellos.

El agente es indiferente entre A y B (o son equivalentes para él) si es igualmente probable que él elija cada opción. Bajo racionalidad perfecta la clara preferencia y la clara indiferencia son las únicas dos relaciones que pueden existir entre dos opciones cuando un agente intenta establecer una comparación entre dos opciones. Luego, se asume que el agente elegirá A (o B), con probabilidad de 0,5 o de uno (por definición, él no puede elegir A con probabilidad de 2/3). Son planteados tres axiomas básicos de las preferencias:

a. Transitividad de la preferencia estricta.

b. Transitividad de la indiferencia.

c. Completitud.

Esta última asegura que dos prospectos seguros, A y B pueden ser comparados. Para los prospectos seguros, A y B, existen tres posibilidades mutuamente excluyentes, o A es preferido a B, o B es preferido a A, o son indiferentes entre sí.

a. y b. son requerimientos de consistencia; c. expresa el requerimiento de que el agente sea capaz de elegir entre cualquier par de prospectos seguros (A y B), considerando su relativa deseabilidad. Si c. no se cumple, él es incapaz de comparar las alternativas A y B. Harsanyi (1989, 29), dejó en claro que la conducta de las personas no siempre confirma estos tres axiomas, "las personas hacen elecciones intransitivas o parecen incapaces de determinar qué prefieren entre un par de alternativas". Empero, para Harsanyi tales desviaciones "no afectan la utilidad de los axiomas como axiomas para una teoría racionalista normativa de la conducta [ ... ] podemos suponer que las desviaciones simplemente representan conductas irracionales atribuible s por ejemplo a las limitadas capacidades de procesamiento de la información por parte de los agentes".

a. b. y c. son equivalentes a los siguientes dos axiomas con respecto a la relación débil de preferencia:

a.* Transitividad de la preferencia débil.

b.* Completitud de la preferencia débil.

Esto último implica que para cualquier par de prospectos seguros, A y B, pueden darse sólo dos relaciones, o A es al menos tan bueno como B, o B es al menos tan bueno como A. Luego, A y B deben estar relacionados.

Recuérdese, Debreu (1959, 7-8), afirmó que una relación de preferencia débil que cumple a* y b* es un "preorden completo".

Sean A y B, prospectos seguros. Sea U una función de valor real definida sobre el conjunto X con la propiedad:

[15]

Entonces U es llamada "función de utilidad" para el individuo i. U representa las preferencias del agente.

Puede verse que si U satisface (15), la elección racional para el individuo i será tratar de maximizar su utilidad con sus elecciones. (15) equivale a (16), que se compone de las siguientes proposiciones:

[16]

Harsanyi (1989) propone dos axiomas sobre la relación de preferencia del agente para definir su comportamiento racional bajo certidumbre:

Axioma 1 (Preorden completo). La relación de preferencia débil es un preorden completo sobre X, que es el conjunto de todos los prospectos seguros. Es decir, esta relación satisface los axiomas a* y b*.

Axioma 2 (Continuidad). Para cualquier prospecto seguro A, tanto su conjunto inferior como su conjunto superior son conjuntos cerrados. Este axioma puede plantearse así: suponga que una secuencia de prospectos seguros B₁ , B₂, ... , converge a un prospecto seguro B₀ y suponga que A es al menos tan bueno como B_i, entonces también ocurre que A es al menos tan bueno como B₀; De igual manera, suponga que la secuencia de prospectos seguros, C_l, C₂, ... , converge a un determinado prospecto seguro, C₀, Y suponga que C_i, es al menos tan bueno como A, entonces también ocurre que C₀ es al menos tan bueno como A.

Teniendo lo anterior presente, puede ser formulado el siguiente teorema:

Teorema 1 (Harsanyi 1989). Si las preferencias del agente entre prospectos seguros satisfacen los Axiomas 1 y 2, entonces existe una función de utilidad continua que representa sus preferencias entre prospectos seguros. Por tanto, la conducta de elección del agente será tal como si él intentase maximizar esa función de utilidad"⁴

Líneas más abajo, Harsanyi aclara que la función de utilidad establecida por el teorema anterior es una función de utilidad ordinal, en este caso definida sobre X, función con la forma:

[17]

Las propiedades de esta función ya son conocidas, son la monotonicidad creciente y la continuidad, para satisfacer (15).

Maximizacián de la utilidad individual en caso de riesgo

En el caso de riesgo se usa una función de utilidad tipo Von NeumannMorgenstern, cardinal, denominada, función de utilidad, U ^e,

U ^e depende de tres axiomas, los axiomas para el comportamiento racional bajo riesgo, que en esencia, son extensiones de los axiomas 1 y 2:

Axioma 1 * (Preorden completo). La relación de preferencia débil es un preorden completo sobre el conjunto Y de todos los prospectos riesgosos.

Axioma 2* (Continuidad). Para cualquier alternativa B, con respecto a cualquier par de alternativas, A y C, tanto el conjunto de probabilidades superior como el inferior son cerrados.

Es más fácil ver a 2* de la siguiente manera. Suponga que la secuencia de probabilidades, p₁, p₂, ... , converge a un determinado punto, p₀ y, suponga que B es al menos tan bueno como (A, p₁; C, 1 - p₁), entonces también ocurre que B es al menos tan bueno como (A, p₀; C, 1 - p₀). Para el caso del conjunto superior haga suposiciones análogas.

Axioma 3* (Monotonicidad en los premios). Suponga que A* es mayor que A y p es mayor que 0, entonces:

[18]

lo inverso también es cierto. Esto significa que el valor de la utilidad de un billete de lotería aumentará si una determinada recompensa A es reemplazada por otra que es preferida A*⁵. Harsanyi en este punto, propone el siguiente:

Teorema 2. Existe una función de utilidad con la propiedad de la U ^e para los prospectos riesgosos:

[19]

U(A) es una función de utilidad para prospectos riesgosos que cumple la propiedad U ^e. Tal teorema establece la existencia de la función de utilidad cardinal, única y preservadora del orden.

Maximización de la utilidad esperada individual en caso de incertidumbre

En el caso de incertidumbre, de acuerdo a la aproximación bayesiana, el propósito de Harsanyi (1989, sección 3.5) será "plantear la existencia de una función de utilidad que tenga la propiedad de la U ^e, no sólo en términos de probabilidades objetivas conocidas por el agente, sino en términos de las propias probabilidades subjetivas que él asigna a los eventos cuyas probabilidades objetivas desconoce". Es decir, se quiere plantear la existencia de una función de utilidad U, que defina la utilidad de cualquier prospecto incierto U(C), como:

[20]

Donde p ^e es la probabilidad subjetiva del agente para el evento e y depende de su ocurrencia y no sólo de las alternativas A y B. Harsanyi se apoya en las ideas de Savage (1954) para demostrar la existencia de tal función de utilidad⁶. La afirmación de que el agente conoce la probabilidad objetiva del evento e, es equivalente a que conozca la frecuencia a largo plazo del evento. Harsanyi propone tres axiomas para el comportamiento racional bajo incertidumbre:

Axioma 1 ** (Preorden completo). La relación de preferencia débil es un preorden completo sobre el conjunto Z de todos los prospectos inciertos.

Axioma 2** (Propiedad de la "utilidad esperada" para prospectos inciertos). El agente tiene una función de utilidad U, en la cual para cualquier prospecto riesgoso, C = (A,p; B, 1 - p), se asigna la utilidad:

[21]

2**, implica que las preferencias del agente entre prospectos riesgosos satisfacen los axiomas 1 *, 2*, 3* así como las convenciones 1, 2, 3. Por el teorema 2 estos axiomas y convenciones implican (21).

Axioma 3** (monotonicidad en los premios para los prospectos inciertos) -principio "sure-thing" o de la cosa segura, para prospectos inciertos-o Suponga que A* es al menos tan bueno como A, entonces:.

[22]

Este axioma implica que si un determinado premio A, es reemplazado por un premio más valorable A*, esto no puede disminuir el valor del billete; éste es el análogo natural para el axioma 3* .

Los tres axiomas de incertidumbre reafirman y extienden los axiomas para el riesgo, y de acuerdo con éstos, puede plantearse el siguiente teorema:

Teorema 3. Existe una función de utilidad con la propiedad de la U ^e en términos de las probabilidades subjetivas del tomador de decisiones. Tal función es

[23]

Claramente, puede verse que como toda construcción dentro de la elección racional estándar, el Modelo de la Utilidad Esperada carece de objeción lógica alguna; es más, ofrece una lógica de la elección.

UNA TEORÍA PSICOLÓGICA DE LA ELECCIÓN

Daniel Kahneman y Amos Tversky, siguiendo a H. A. Simon, se dedicaron a estudiar cómo las creencias de los agentes inciden en la toma de decisiones. Lejos de encontrar seres que ostentan creencias objetivas y efectúan engorrosos y sofisticados procesos de elección racional, los mencionados autores mostraron que las personas tienen sesgos cognitivos, sufren intuiciones (muchas veces impulsadas y realzadas por emociones) y usan heurísticas cuando deciden. La parte sustancial de estos aportes está condensada en Kahneman (2000, 2002). Enseguida se hace una presentación de sus elementos básicos.

Sobre la escogencia intuitiva

En el mundo real, las escogencias humanas distan de los supuestos ideales de la elección racional y del platónico modelo de la utilidad esperada. Elster (1999) advierte que la elección racional solamente puede expresar los intereses (puesto que las emociones y las razones no son objeto de decisiones racionales). Por su parte H. Simon (1989, 22.) muestra que la teoría de la utilidad esperada abarca toda la diversidad de valores humanos (razones, sentimientos, pasiones e intereses diversos) dentro de una sola función. Ya Elster (1983) había hecho énfasis en que una teoría amplia de la racionalidad debería sugerir unos fines humanos constructivos (distintos, por ejemplo, a la codicia y a la envidia), y señalar unas creencias que tiendan a ser verdaderas (o al menos objetivas).

Uno de los méritos de Kahneman y Tversky es su trabajo empírico (experimentación con seres humanos), lo cual rompe con la estéril metodología de la abstracción suprema (mediante la cual se supone, cual un acto de fe, que los individuos se comportan conforme a los principios prescriptivos de la teoría de la elección racional). En términos generales, su hallazgo global es que las personas, con frecuencia, deciden intuitivamente (mediante impresiones) y no por medio de juicios (que resultarían de un proceso de escogencia tan dispendioso y calculado como el postulado por los teóricos de la elección racional). Una buena síntesis se encuentra en Gilovich, Griffin y Kahneman (2002).

Como se ilustra en la Gráfica 1, las personas suelen decidir a partir de intuiciones (basadas en impresiones) y no tanto por medio de juicios que resulten de una escogencia racional engorrosa y deliberada. Puesto en breve: el sistema perceptivo de la persona y las operaciones intuitivas del sistema 1 generan impresiones: los juicios intuitivos reflejan directamente las impresiones. Tal observación ayuda a conocer algunos rasgos de la escogencia humana, destacando los siguientes: a) al decidir, con frecuencia, las personas ubican la cualidad más accesible del objeto de escogencia (deciden al ver la primera impresión); b) la gente se suele concentrar en el rasgo más sobresaliente o exagerado de un objeto o situación y al obrar así es afectada por alguna emoción; e) antes que escoger fría y calculadamente entre varias opciones, las personas suelen elegir bajo presión y, a priori, se enamoran o inclinan por determinada alternativa.

Una consecuencia de la escogencia intuitiva es que en contra de uno de los supuestos capitales de la teoría de la elección racional, las personas no poseen preferencias dadas e invariables, sino que más bien éstas se forman en el proceso mismo de la elección y, como si esto fuese poco, los ordenamientos de preferencias se alteran dependiendo de los diversos contextos de la escogencia. Se destacan dos evidencias fundamentales de la elección intuitiva expuesta en diversos trabajos de Kahneman y Tversky, a saber: los efectos de encuadre y la función de utilidad sensible a los cambios (pérdidas o ganancias) a partir de un punto de referencia (denominado status quo).

La existencia de efectos de encuadre es una evidencia de tal calibre que, prácticamente, invalida los supuestos de invarianza (extensionalidad) y de independencia de las alternativas irrelevantes, los cuales son de gran importancia para la teoría de elección racional. La gente es sensible a la manera como se le presenta un problema (no es lo mismo afirmar que de un universo de 600 personas se salvarán 200 vidas, a decir que de 600 personas se perderán 400 vidas), aunque no varíe la información objetiva. Los individuos del mundo real son sensibles a la introducción de alternativas (en realidad relevantes) a su menú de elección: suele suceder, por ejemplo, que la existencia de un apartamento medianamente cercano y de precio intermedio altere la elección (ordenamiento de preferencias) entre uno distante y muy barato, y uno más cercano pero muy caro.

Kahneman y Tversky y Slovic (1982) concibieron el proceso de elección ante todo como un proceso mental de estimación intuitiva de cantidades, probabilidades y valores numéricos, orientado a la comparación y evaluación de éstos con algún estándar preestablecido:

"las creencias son expresadas en frases del tipo "yo pienso que ... ",

"las oportunidades son ... ", "es improbable que ... ", ... ocasionalmente, las creencias considerando ciertos eventos son expresadas en forma numérica como probabilidades. Proponemos que la gente confia en un número limitado de heurísticas que reducen las complicadas tareas de cálculo de probabilidades y de predicción de valores a operaciones de estimación mucho más simples" (Kahneman, Tversky y Slovic, 1982, cap. 1 )

El carácter intuitivo de este proceso le confiere tres rasgos que pueden ser tan deseables como indeseables: es un proceso del cual el agente no conoce todas sus etapas, y es por lo tanto automático y emotivo. Entonces, el agente para economizar tiempo y esfuerzo en la toma de decisiones, usa una serie de reglas empíricas o heurlsticas⁷ que conducen a errores sistemáticos o a sesgos que no serán detallados aquí. Los experimentos realizados durante las tres últimas décadas del siglo pasado permitieron a estos autores corroborar observaciones que no eran nuevas.

1. La mayoría de personas hace estimaciones de probabilidad que no concuerdan con las leyes de probabilidad (bayesianas). Debe mencionarse que Meehl en 1954, contrastando las predicciones estadísticas con las predicciones clínicas, en un artículo del mismo nombre, había hecho una afirmación en el mismo sentido (Kahneman y Tversky 2000).

2. La mayoría de personas no valora las consecuencias de sus acciones en un sentido absoluto; ellos hacen evaluaciones de sus resultados relativos a ciertos puntos de referencia establecidos por ellos mismos.

Lejos de un sofisticado proceso de cálculo como el que se propone en los modelos de decisión racional, "el cálculo de cantidades subjetivas semeja el cálculo subjetivo de magnitudes fisicas tales como la distancia y el tamaño" repiten vez tras vez Kahneman y Tversky en sus escritos.

La formulación más antigua de la Teoría de Prospectos vio la luz en 1979 y ofreció una alternativa adicional⁸ a las existentes sobre la toma de decisiones riesgosas. En aras de la brevedad, Kahneman y Tversky propusieron la siguiente función de valoración subjetiva para prospectos riesgosos con n resultados:

[24]

π (p) son funciones de las probabilidades asociadas a cada alternativa denominadas por Kahneman y Tversky, funciones de ponderación; mientras que las v (x) son llamadas funciones de valoración subjetiva.

Para prospectos binarios estrictamente positivos (x_i > O), o estrictamente negativos (x_i < 0), que son colectivamente exhaustivos (∑ p_i = 1), fueron ofrecidas las funciones de valoración subjetiva

[25]

que expresan el principio de segregación por el cual un prospecto binario riesgoso es mentalmente evaluado partiendo de sus dos componentes, uno sin riesgo que es el resultado mínimo cierto que el agente espera obtener de su decisión y uno riesgoso que es el resultado derivado del carácter azaroso de su situación. Componentes que respectivamente son el primer y segundo sumandos de (25) donde se ha asumido que x_l > x₂ y p₁ < p₂.

La valoración subjetiva de un prospecto riesgoso dependerá entonces de dos funciones:

1. Una función de ponderación, definida sobre las probabilidades, π (p) con π (p) ε [0,1] y,

2. Una función de valoración subjetiva para cada posible resultado, v (x).

Las características de estas funciones serán descritas a continuación.

La función de ponderación

La función aludida es una transformación no lineal de las probabilidades asignadas a cada uno de los resultados del prospecto riesgoso. En 1984 (reimpreso en 2000) estos autores ofrecen una representación preliminar de la función de ponderación como explicación de la aversión al riesgo en el dominio de las ganancias⁹ y de la búsqueda del riesgo en el dominio de las pérdidas por parte de los agentes. Esta función fue representada como aparece en la Gráfica 2.

En contraste con la Teoría de la Utilidad Esperada que asume que las ponderaciones de los resultados corresponden a sus probabilidades, la función de ponderación de la Teoría de Prospectos expresa el hecho de que las ponderaciones no son iguales a las probabilidades excepto para las probabilidades extremas, esto es, π (0) = 0 y π (1) = 1.

Esta función de ponderación se caracterizó por:

1. Sobreponderación de las bajas probabilidades.

2. Subponderación de las probabilidades intermedias y altas.

3. Ponderaciones iguales para ganancias y para pérdidas.

Las ponderaciones en la Teoría de Prospectos son inferidas de las elecciones entre prospectos tal como las probabilidades subjetivas son inferidas en la aproximación Savage-Ramsey. Las ponderaciones no son probabilidades porque no obedecen a los axiomas de la probabilidad y por ello no deben ser interpretadas como medidas del grado de creencia.

La función de valoración subjetiva

De acuerdo con Kahneman (2002), una propiedad general de los sistemas perceptivos (Gráfica 1) es que permiten realzar la accesibilidad de los cambios y las diferencias y, además, la percepción depende de un marco de referencia. Así las cosas, los atributos percibidos de un estímulo notable reflejan el contraste entre el estímulo y el contexto previo a la ocurrencia de tal impulso. Por cierto, la dependencia de un punto de referencia es incompatible con la interpretación estándar de la teoría de la utilidad esperada. Kahneman y Tversky dicen que esta idea surgió como una adecuación natural de la Teoría del Nivel de Adaptación de Helson (1955), según la cual la evaluación de un estímulo fisico depende de la magnitud de la intensidad de ese estímulo relativa a algún nivel de referencia.

Puede decirse que el pilar fundamental de la Teoría de Prospectos Riesgosos fue el planteamiento de una función de valor subjetiva definida no sobre estados finales de riqueza sino sobre ganancias y pérdidas, con relación a un punto de referencia que usualmente es el status quo del elector. Por consiguiente las preferencias son dependientes del status quo de quien decide. En la Gráfica 3 (la función subjetiva del valor), se advierte que los individuos cuando eligen discriminan entre pérdidas y ganancias, que subjetivamente las pérdidas pesan más que las ganancias (la función es cóncava en el terreno de las ganancias y convexa y más inclinada en el de las pérdidas).

Se asume que los individuos experimentan una utilidad subjetiva, de placer o desagrado, en relación con la percepción de pérdidas y ganancias.

La función subjetiva de valor es asimétrica, dado que las pérdidas tienen más impacto que las ganancias: la pena de perder 200 dólares casi no se quita con la suerte de ganar 400 dólares. La teoría de los prospectos de Kahneman y Tversky muestra que los individuos suelen estar preocupados por resultados de corto plazo y su función subjetiva del valor expresa que existe una valoración emocional asociada a los cambios de riqueza (pérdidas o ganancias). La utilidad no puede estar divorciada de la emoción y las emociones son activadas por cambios en los estados o contextos de la escogencia.

Una representación de la función de valoración subjetiva en el plano x - V (x), es una curva en forma de S, cóncava en el cuadrante III y convexa en el primero, expresada por medio de una fórmula tipo:

[26]

Donde x es el pago recibido; σ es un coeficiente de aversión relativa al riesgo obviamente constante (σ > 0) y λ es el factor de aversión a perder que ha sido estimado en tomo a -2, 5. El factor de aversión a perder indica el número de veces que una pérdida es estimada subjetivamente relativa a una ganancia del mismo tamaño, es decir, este factor es la razón entre las valoraciones subjetivas de una pérdida y una ganancia del mismo tamaño:

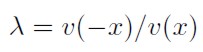[27]

Esta función de valor se caracteriza por:

1. Aversión a perder: a la gente le disgusta más una pérdida de lo que le gusta una ganancia del mismo tamaño, esto es:

[28]

2. Sensibilidad decreciente: el impacto de un cambio en las ganancias o en las pérdidas es menor a medida que este se aleja del punto de referencia. La sensibilidad decreciente implica que la función de valor sea cóncava en el dominio de las ganancias, v" (x) < 0 y convexa en el dominio de las pérdidas, v" (x) > 0.

La sensibilidad decreciente implica que la función de valor sea cóncava en el dominio de las ganancias, v" (x) < 0 y convexa en el dominio de las pérdidas, v" (x) > 0

Teoría de prospectos acumulativa

Durante la segunda mitad de los años ochenta fueron observados comportamientos más complejos ante el riesgo: la aversión a éste para ganancias de alta probabilidad y pérdidas de baja probabilidad y la búsqueda del riesgo para ganancias de baja probabilidad y pérdidas de alta probabilidad. Tales actitudes ahora conocidas como el cuádruple patrón de actitudes ante el riesgo; no podían ser explicadas dentro de la teoría de prospectos riesgosos y, por tanto, se asumieron ponderaciones iguales tanto para ganancias como para pérdidas. Buscando solucionar estos inconvenientes Tversky y Kahneman (1992, reimpreso en 2000) formularon una "Teoría Acumulativa de Prospectos" (Cumulative prospect theory).

Fue necesario alterar la condición 3 (sobre la igualdad de la funciones de ponderación para ganancias y pérdidas) y plantear una cuarta condición sobre la función de ponderación de probabilidades para lograr explicar el cuádruple patrón de actitudes ante el riesgo. Estos cambios en la función de ponderación fueron realizados en Tversky y Kahneman (1992, reimpreso en 2000).

Explícitamente, los autores propusieron las siguientes cuatro características propias de la función de ponderación subjetiva:

1. Sobreponderación de las bajas probabilidades.

2. Subponderación de las probabilidades intermedias y altas.

3. Ponderaciones diferentes para ganancias y para pérdidas.

4. Sensibilidad decreciente para la función de ponderación.

Esta última implica que el impacto en un cambio de la probabilidad disminuye a medida que aumenta su distancia relativa a las probabilidades extremas, es decir, el impacto de un paso de la posibilidad a la certeza o de la posibilidad a la imposibilidad es mayor que un cambio ocurrido en los rangos medios de probabilidad, patrón que ha sido llamado subaditividad (Tversky y Fox 1995, Prelec 2000). La sensibilidad decreciente también explicó un principio formulado en 1979, la subproporcionalidad por el cual

"para una razón fija de probabilidades, la razón de las correspondientes ponderaciones es más cercana a 1 cuando las probabilidades son bajas que cuando son altas. Tal propiedad (Subproporcionalidad) impone considerables restricciones a la forma de la función de ponderación" (Kahneman y Tversky 1979, 282; Kahneman et al. 2000, capítulos 2 y 3).

La Teoría Acumulativa de Prospectos puede ser representada por las siguientes fórmulas:

1. Para prospectos simples tipo (x, p) con un resultado no 0,

[29]

2. Para prospectos binarios tipo (x_l, p₁; x₂, p₂) con dos resultado no 0 y se tiene que:

[30]

[31]

[32]

donde w son las funciones de ponderación diferenciales dependiendo del signo del resultado obtenido que serán w⁺ y w^- para resultados positivos (ganancias) y negativos (pérdidas), respectivamente.

La representación gráfica de la función de ponderación ofrecida por Kahneman y Tversky (1992) a partir de sus propias estimaciones se presenta a continuación.

Nótese que la curva más volátil es la función de ponderación para ganancias. Las funciones de ponderación que satisfacen estas condiciones han sido evaluadas por Camerer y Ha (1994) Y Gonzáles (1996a) en el caso de funciones con un parámetro, y por Tversky y Fax (1995, en Kahneman et al. 2000) en el caso de funciones con dos parámetros. Prelec (2000, en Kahneman et al. 2000) ofrece una versión de la función de ponderación similar a la de la Gráfica 2 partiendo de la fórmula:

Donde α es un parámetro estimado en 0,36 aproximadamente. Bajo la égida de la Teoría Acumulativa de Prospectos, el determinante fundamental del cuádruple patrón de actitudes ante el riesgo ha llegado a ser la no linealidad de las probabilidades expresada por la función de ponderación.

Algunos axiomas de la teoría de la utilidad esperada violados en las elecciones cotidianas

Kahneman y Tversky (1979, 1986, 1992 reimpresos en 2000), describen cuatro principios cualitativos de carácter sustantivo o axiomas que deberían gobernar las elecciones de un agente racional, esto es, maximizador de la utilidad, cuando afronta decisiones entre prospectos riesgosos o inciertos:

1. Transitividad.

2. Sustitución ¹⁰: si el prospecto A es preferido al prospecto B entonces un chance igual de obtener A o un tercer prospecto C es preferido a un chance igual de obtener B o C. Desde 1986, este axioma de la elección racional fue llamado por estos autores como cancelación, que expresa una eliminación de cualquier estado de la naturaleza que rinda el mismo resultado.

3. Dominancia: si el prospecto A es preferido débilmente al B en todos excepto en un aspecto en el que A es preferido estrictamente a B, entonces A será preferido estrictamente a B.

4. Invarianza procedimental: el orden de las preferencias entre prospectos no debe ser alterado por la forma en que los prospectos son descritos. La invarianza implica que dos versiones lógicamente equivalentes de un problema de elección deben rendir las mismas decisiones.

Los axiomas anteriores están tras supuestos más técnicos como la continuidad. Ninguno de estos axiomas ha sido observado por personas ingenuas o expertas, ni corregido con incentivos materiales como pagos monetarios elevados¹¹ ni adoptando procedimientos para que las personas evalúen los prospectos en términos de sus activos totales. Es obligación aclarar que en ningún momento la Teoría de Prospectos se ha basado en un ataque sistemático de los axiomas de la elección racional como lo hizo Simon en repetidas ocasiones (particularmente en 1989), sino en una búsqueda de alternativas descriptivas válidas que puedan ajustarse a los resultados hallados y a las conductas no explicadas dentro de la racionalidad estándar.

ALGUNOS FENOMENOS QUE NO SE AJUSTAN A LOS RESULTADOS DE LOS MODELOS DE UTILIDAD ESPERADA

En esta sección no se tiene otra pretensión que esbozar algunos problemas que, en aras de un análisis más realista, requieren un tratamiento más cercano a la teoría de los prospectos de Kahneman y Tversky, estos son:

Equity premium. Alude al mayor retomo que reciben las acciones u otros papeles de renta variable con relación al retomo recibido por papeles de renta fija como los bonos. Mehra y Prescott (1985, en Kahneman et al. 2000, capítulos 14, 16 y 17) observando un retomo para los stocks superior en 8 % anual al retomo de los bonos desde 1920s, afirmaron que bajo los supuestos de la teoría económica estándar este patrón implicaba una conducta absurdamente aversa al riesgo por parte de los inversionistas, para demandar tan alta prima por la tenencia de activos riesgosos. Kahneman et al. 2000, muestran con la ayuda de la Teoría de Prospectos, que los inversionistas no son aversos a la variabilidad de los retornos sino aversos a perder. Como los retornos anuales sobre los stocks son mucho más frecuentemente negativos de lo que lo son los de los bonos, las inversiones "aversas a perder" ("loss averse") demandarán una mayor prima.

Efecto disposición. La gente es propensa a mantener stocks que han perdido valor demasiado tiempo y venden los "ganadores" demasiado pronto, afirma Odean (citado por Kahneman et al. 2000, cap. 21).

Sobre la tasa marginal intertemporal de sustitución entre trabajo y ocio. Lucas y Rapping en 1969 propusieron un modelo con sustitución intertemporal entre trabajo yacio para explicar la relación positiva, a nivel agregado, entre el producto y el empleo, asociada con pequeños movimientos en el salario real. Específicamente, argumentaron que pequeños cambios temporales en el salario real ocasionarían una respuesta en la oferta laboral, con "trabajadores dispuestos a sustituir ocio por trabajo de los períodos en que el salario es alto a los períodos en los que el salario es bajo", supuesto que requiere de un mercado laboral flexible e implica simplemente que los trabajadores de este mercado trabajaran más horas cuando el salario es alto y menos horas cuando el salario es bajo. Camerer et al. (1997, 407- 441; Kahneman et al. 2000, 356-70) estudiaron un mercado laboral con las características requeridas, los taxistas neoyorquinos. Ellos partieron de la hipótesis de que los taxistas fijan un ingreso objetivo diario como límite para su oferta laboral, hipótesis que implica que los taxistas tendrán que trabajar más horas los días "malos" cuando su ingreso por hora es bajo, en la consecución de su ingreso objetivo y, trabajarán menos tiempo los días "buenos" cuando su ingreso por hora es alto, lo que les permite alcanzar más rápido su ingreso objetivo, implicación que desde la teoría económica estándar es claramente ineficiente. Los resultados del análisis de los datos recogidos por Camerer y su equipo, mostraron una fuerte correlación negativa entre los salarios por hora de los taxistas y el número de horas trabajadas, esto significa que las taxistas tienen "horizontes de un díaz tienen una función de utilidad para el ingreso diario obtenido que se curva en el ingreso diario objetivo.

Sobre las elasticidades de precios asimétricas para los bienes de consumo. A los consumidores les desagrada más un aumento en el precio de lo que les agrada una disminución del mismo; consecuentemente, sus compras disminuirán más cuando los precios aumenten, de lo que se incrementan cuando los precios disminuyen. Evidencia sobre esta conducta de los consumidores se encuentra en Kahneman et al. 2000, capítulos 16 y 42).

Sobre las decisiones de ahorro y consumo. Un resultado central de los modelos sobre asignación intertemporal de recursos, es que las personas gastarán hoy más a la vista de ingresos futuros altos y recortarán sus gastos hoy cuando esperan ingresos futuros bajos. Shea (1992, 1995) ha revisado este fenomeno. Por ejemplo, para un grupo de profesores universitarios sindicalizados cuyo contrato era negociado con un año de antelación, que los profesores gastaron más cuando esperaban salarios al alza, pero no disminuyeron su consumo cuando sus salarios futuros fueron recortados.

Sobre la elección del consumidor. Las personas padecen de un sesgo de status quo (Zeckhauser 1996) por el cual la retención del status quo es una opción preferida en muchos problemas de decisión. El sesgo de status quo ya había sido referido en Thaler (1980), como efecto dotación y significa que la pérdida de utilidad asociada con ceder un bien es mayor que la ganancia de la utilidad asociada con recibirlo. Luego, el valor subjetivo de un bien parece cambiar cuando el bien es incorporado en la dotación de un agente. Este sesgo o efecto es una consecuencia natural de la aversión a perder e implica que existen bienes cuyas curvas de indiferencia no son reversibles (Kahneman et al. 2000, capítulos 7,8 y 9). Como se sabrá, una curva de indiferencia indica los tradeoffs correspondientes entre dos bienes y esta tasa de sustitución es la misma en un punto de una curva de indiferencia en cualquier dirección.

Los sesgos para mantener el estatus quo, la guerra y la ley. Un hallazgo notable de los diversos trabajos de Kahneman y Tversky (2000), discutidos en Arrow (1995) Y en Cante (2006 y 2008) es que las personas suelen aferrarse a su status quo y suelen renunciar a éste si les otorgan mucho más de lo que ellas deben ceder (lo que obedece a la aversión a perder). Esto tiene importantes implicaciones para los estudios sobre la negociación, la guerra y la ley, entre los que se destacan:

• La posibilidad de acuerdos se reduce notoriamente cuando los negociadores o bandos en conflicto se aferran a un status quo, puesto que cada parte busca recibir más que el doble de lo que cede. La persistencia del desacuerdo se incrementa si el status quo de las partes corresponde a posiciones extremas (cuando cada parte se aferra a un extremo y su antagonista a la posición adversa).
• Las guerras suelen escalarse y perpetuarse porque, posiblemente en razón de la aversión a perder y los sesgos a mantener un status quo, la milenaria ley del talión no es simétrica (ojo por ojo) sino sesgada (si me sacan un ojo, entonces saco dos ojos al enemigo).
• La ley tiende a favorecer el conservadurismo y a ser paretiana (en el sentido de favorecer el status quo). La posesión es nueve décimos de la ley, reza el dicho anglosajón. Y los derechos adquiridos se suelen defender con más ímpetu (intensidad) que los derechos que aún no existen.

CONCLUSIONES

Los modelos económicos derivados de la racionalidad estándar no son infalibles. Divergencias entre teorías positivas y normativas surgen a cada momento y la brecha entre la inadecuación de una teoría a la realidad no puede ser soslayada por ninguna cantidad de "argumentos teóricos" que estén soportados en supuestos equivocados (por lo hondamente irreales). La Teoría de Prospectos contiene al menos tres elementos que pueden explicar varias predicciones contraintuitivas ofrecidas por los modelos normativos:

1. La función de valoración definida para ganancias y pérdidas relativas a un punto de referencia.

2. La aversión a perder. Un supuesto ofrecido por Read, Loewenstein, Rabin y Thaler por el cualísla unas decisiones de otras que podrían ser agrupadas con ella" (en Camerer, 1995, 1997, 1998; Rabin 1998; Kahneman et al. 2000, 287; Kahneman et al. 2002).

La incorporación de varios rasgos psicológicos, como la aversión a perder o al riesgo y la sensibilidad decreciente frente a un estímulo, que caracterizan la conducta humana ante la toma de decisiones riesgosas o inciertas permite a la Teoría de Prospectos ofrecer una alternativa válida dentro del análisis de decisión al modelo de la utilidad esperada. Particularmente, esta teoría descriptiva explica una serie de conductas que dentro de la racionalidad estándar no tienen cabida y que de aparecer son etiquetadas como "irracionales", asumidas como "marginales" y por ello dejadas a la deriva y sin explicación, conductas que antes de ser la excepción son la norma como las siguientes:

• La no aplicación de las leyes de la probabilidad.
• La no evaluación de los resultados en términos de estados finales de riqueza.
• La influencia del contexto en las elecciones a través del "framing" de las opciones.
• La influencia de ciertos estados motivacionales en las elecciones teniendo en cuenta que toda elección, aunque con disímil intensidad, está imbuida de alguna emoción¹² efectiva o disposicional e implica un juicio de valor ético del que la teoría económica no ha podido desprenderse y recientemente ha intentado incorporar, este es el caso de la nociones de justicia que afectan las elecciones en los juegos bipersonales ¹³.

Todas estas conductas alteran las predicciones ofrecidas (en tomo a la elección individual) desde los modelos fieles a la lógica de la racionalidad estándar que en términos generales, parten de un agente maximizador de la utilidad, omnisciente y dotado de unas excepcional capacidad de cálculo.

Sería pretensioso y aún contradictorio abogar por una teoría más (una nueva pretensión de dictar leyes generales), alterna a la elección racional. Esfuerzos como los de H. A. Simon, 1. Elster, Kahneman y Tversky, señalan la importancia enorme del trabajo empírico y la experimentación. No se puede persistir en la ficción de suponer que las personas se comportan como lo dictaminan los caprichos del teórico, es imperativo que este observe la realidad y compruebe cómo se comporta la gente de carne, hueso y sentimientos.

NOTAS AL PIE

1 En el presente artículo, se entenderá por prospecto (prospect) a "cualquier lista de consecuencias derivadas de una elección con sus respectivas probabilidades" (Starmer 2000, 335). Sin embargo, no se usará el término expectativa (expectation) para evitar confundirlo con términos más concretos como el de valor esperadc.texpected value) de una variable aleatoria o la utilidad esperada (expected utility) asociada a una decisión.

2 Tratada también por Delquié 200l. El antecedente de Dissapointment theory fue la Regret theory tratada por los mismos autores independientemente en 1982. Ver Santiago 2003, 75; Starmer 2000; Sirvent 1994; Delquié 2000.

3 La utilidad procedimental parte de la idea en virtud de la cual el agente incorpora al momento de decidir, aspectos relacionados con los procesos para obtener las consecuencias que se buscan con la decisión, de los cuales también deriva utilidad. Entonces, se propone una función de utilidad no solamente consecuencialista que contemple tales aspectos procedimentales de la toma de decisiones. Scitovsky (1978), describió cómo las personas derivan satisfacción no sólo de las consecuencias de una acción sino de la acción que les lleva a las consecuencias en sí misma, Frey (2000, 2002), Le Menestrel (2001) Y Stutzer y Frey (2006) usan tal concepción en sus investigaciones.

4 La prueba de esta afirmación de Harsanyi está en Debreu (1959, 55-59).

5 Harsanyi (1982, 40) afirma que su principio de sustitución (axioma 3*), es similar al principio "sure-thing" de Savage (1954, 21-26), pero para Harsanyi 3* es más débil dado que implica que "el valor del billete no puede disminuir si un premio dado A es reemplazado por un premio más valorado, A*".

6 También se apoya en otros autores como Pratt, Raiffa y Schlaifer (1964). Estos autores también sustentan los argumentos de Shubik (1989), quien dispone de una bibliografia mucho más amplia.

7 "Las heurísticas no se prestan al análisis formal porque su aplicación depende de la formulación del problema, del método de "sonsacamiento" -obtención- ("elicitation") y del contexto de la elección" (Kahneman et al. 2000, 66).

8 0tros modelos alternativos al de la Utilidad Esperada han sido presentados en Allais (1954), Coornbs (1975), Fishburn (1978, 1989) Y (Kahnernan y Tversky, 2000). El lector interesado es remitido a los textos de Machina, particularmente los publicados en 1982 y en 1989.

9 Dentro de la teoría económica estándar la aversión al riesgo es sinónimo de la concavidad de la función de utilidad definida sobre estados finales de riqueza y ha sido explicada por la utilidad marginal decreciente de ésta, una explicación errónea para Rabin (1997) quien afirmó que los niveles de aversión al riesgo requeridos para que la función de utilidad sea cóncava son absurdamente ridículos.

10 Kahneman y Tversky (1986 en Kahneman et al. 2000,209-223) escribieron que Von Neumann y Morgenstern lo llamaron así en 1944, pero Machina (1982, 278) que lo denominó "independencia", en una nota al pie de página afirmó que en la formulación original de Von Neumann y Morgenstem este axioma no apareció explícitamente, aunque ellos reconocieron, como lo hicieron Kahneman y Tversky, que la Teoría de la utilidad esperada dependía crucialmente de la validez empírica de este axioma. En el mismo texto, Kahneman y Tversky equipararon este axioma con las propiedades formales del "Principio Cosa Segura" de Savage (1954) y con la "Condición de Independencia" de Luce y Krantz (1971).

11 Las mayores violaciones del modelo de la utilidad esperada han ocurrido con o sin incentivos y sin importar que tan grandes eran estos en términos monetarios, como fue comprobado en el estudio de Kachelmeier et al. (1992) que ofrecieron incentivos con tres y cuatro dígitos por sesión a sus sujetos. Comúnmente se aduce como crítica que estos incentivos monetarios son relativamente pequeños cuando son comparados con el ingreso de los participantes; asunto que no fue el caso del estudio en cuestión. Los sujetos en la condición de alto pago recibieron tres veces su ingreso mensual en una sola sesión. Camerer 1989, 1997 y 1998 (en Kahneman et al., 2000, cap 16) y Kahneman y Tversky (1992) describen los aportes de Kachelmeier y de otros evaluadores de la Teoría de Prospectos.

12 Frank (1988) desarrolla un modelo de compromiso que apela a las emociones ocurrentes o a las disposicionales para entablar una conducta estratégica en juegos bipersonales.

13 Ver Rabin (1997), Lakatos (2002), Camerer (2002) y Gintis et al. 2005).

REFERENCIAS BIBLIOGRÁFICAS

1. Allais, M. (2003). "Le Comportement de I'Homme Rationnel devant le Risque: Critique des Postulats et Axiomes de l'Ecole Americaine. Econometrica", Econometrica, 21(4): 503-546. Disponible en: http://www.jstor.org/stable/1907921. Consultado el 12 de septiembre de 2008.        [ Links ]

2. Allais, M. (1954). "Puissance et Dangers de l'Utilisation de l'Outil Mathematique Economique". Econometrica, 22 (1): 58-71. Disponible en: http://www.jstor.org/stable/1909833. Consu1ato el 12 de septiembre de 2008.         [ Links ]

3. Arrow, J. (1995). Barriers to Conflict Resolution. New York: W. W. Norton & Company.         [ Links ]

4. Bell, D.E. (1985). Putting a premium on regret. Management Science, 29: 1156- 1166.         [ Links ]

5. Benartzi, S., R. Michaely y R. Thaler (1997). "Do Dividends Signal the Future or the Past?". Journal of Finance, 52 (3): 1007-1034.         [ Links ]

6. Camerer, C. y Weber, R. (1999). "The econometrics and behavioral economics of escalation of commitment: A re-examination of Staw and Hoang's NBA data". Working Paper 1043, California Institute of Technology, Division ofthe Humanities and Social Sciences.         [ Links ]

7. Camerer, C. (1997). "Taxi Drivers and Beauty Contests". Engineering and Science, 1: 10-19.         [ Links ]

8. Camerer, C. (2003). Behavioral Game Theory, Experiments in Strategic Interaction. Princeton, New Jersey: Princeton University Press.         [ Links ]

9. Camerer, C. y Ho T-H. (1994). "Violations ofthe Betweenness Axiom and Nonlinearity in Probability". Journal of Risk and Uncertainty, 8: 167-196.         [ Links ]

10. Cante, F. (2006). "Libertad real y algunos problemas de formación de preferencias". En Cante, F. y Mockus, A. Acción colectiva, racionalidad y compromisos previos. Bogotá: Unibiblos, Universidad Nacional de Colombia.         [ Links ]

11. Cante, F. (2008). Libertades individuales y oportunidades factibles. Tesis Doctoral. Bogotá: Universidad Nacional de Colombia, Facultad de Ciencias Económicas. 2008.         [ Links ]

12. Cante, F. Y Mockus, A. (compiladores) (2006). Acción colectiva, racionalidad y compromisos previos. Bogotá: Unibiblos, Universidad Nacional de Colombia.         [ Links ]

13. Coombs, C. H. (1975). Portfolio theory and the measurement of risk. In M. F. Kaplan & S. Schwartz (Eds.), Human judgment and decision. Minneapolis: Minnesota University Press.         [ Links ]

14. Debreu, G. (1959). "Cardinal utility for even chance mixtures of pairs of sure prospects", Review of Economic Studies, 71: 174-177. Disponible http://cepa.newschool.edu/het/profiles/debreu.htm. Consultado el 10 de septiembre de 2003.         [ Links ]

15. Delquié P. (1993). "Inconsistent Trade OfIs Between Attributes Assessment issues: new evidence in preference assesment biases". Management Science, 39 (11): 1382-1395.         [ Links ]

16. Delquié, P. (2001). Modeling Dissapointment In Risky Choice: A Proposal Fontainebleau. Paris: INSEAD.         [ Links ]

17. Edwards. w., Janis, 1. y Mann. 1. (1961). "Behavioral decision theory". Decision Making: A Psychological Analysis of Conflict, Annual Review of Psychology Choice 12: 473-498.         [ Links ]

18. Elster, J. (1983). Sour Grapes. Cambridge: Cambridge University Press.         [ Links ]

19. Elster, J. (1999). Alchemies ofthe Mind: Rationality and the Emotions. Cambridge: Cambridge University Press.         [ Links ]

20. Elster, J. (2002). "La teoría de la elección racional y sus rivales", en Cante, F. y Mockus, A. Acción colectiva, racionalidad y compromisos previos. Bogotá: Unibiblos, Universidad Nacional de Colombia.         [ Links ]

21. Fishburn, P. (1978). "A Probabilistic Expected Utility Theory of Risky Binary Choices". International Economic Review, 19 (3): 633-646. Disponible en: http://www.jstor.org/stable/2526329.         [ Links ]

22. Fishburn, P. (1989). "Foundations of Decision Analysis: Along the Way". Management Science, 35(4): 387-405. Disponible en: http://www.jstor.org/stable/2631888        [ Links ]

23. Frey, B., Stutzer, A. (2000). "Happiness, Economy And Institutions". The Economic Journal, 110(466): 918-938. Disponible en http://www.jstor.org/stable/2667858. Consultado el l0 de julio de 2008.         [ Links ]

24. Frey, B., Benz, M. y Stutzer, A. (2002). "Introducing Procedural Utility: Not Only What, But AIso How Matters". Working Paper Series, 129. Institute For Empirical Research In Economics. University Of Zurich. Disponible en http://www.iew.uzh.ch/index.html. Consultado el l0 de julio de 2008.         [ Links ]

25. Frank, R. (1988). Passions within reason: the strategic role of emotions. New York: W. W. and Norton. 1988.         [ Links ]

26. Fox, C. R. y (1995). "Ambiguity Aversion and Comparative Ignorance". The Quarterly Journal of Economics, 110(3): 585-603.         [ Links ]

27. Gilovich, T., Griffin, D. y Kahneman, D. (2002) "Heuristics and Biases. The Psychology Of Intuitive Judgment", Cambridge: Cambridge University Press.         [ Links ]

28. Gintis, H., Bowles, S., Boy, R., y Fehr, E. (eds). (2005). Moral Sentiments and Material Interest. Cambridge, Mass: MIT University Press.         [ Links ]

29. Harsanyi, 1. (1989). Rational Behavior and Bargaining Equilibrium In Games and Social Situations. New York: Cambridge University Press.         [ Links ]

30. Hayek, F. (1978) "La pretensión del conocimiento", en Premios Nóbel de Economía. México, FCE.         [ Links ]

31. Hayek, F. A. (1984). "Social or Distributive Justice and " The Pretence of Knowledge", in The essence 0f Hayek, (Edited by Nishiyama and Leude), Hoover Institution Press, Stanford.         [ Links ]

32. Helson, H. Y Himelstein, P. (1955). "A Short Method for Calculating the AdaptationLevel for Absolute and Comparative Rating Judgments". The American Journal of Psychology, 68 (4): 631-637. Disponible en: http://www.jstor.org/stable/1418791.        [ Links ]

33. Kachelmeier S. J. y Shehata M. (1992). "Examining risk preferences under high monetary incentives: Experimental evidence from the People's Republic China". The American Economic Review 82: 1120-1141.         [ Links ]

34. Kahneman, D. (2002). Maps of Bounded Rationality: A Perspective on Intuitive Judgement and Choice. (Nobel Prize Lecture). Princeton: Princeton University, Department of Psychology.         [ Links ]

35. Kahneman, D. (2000). Choices, Values and Frames. Cambridge, Mass: Cambridge University Press & Russell Sage Foundation.         [ Links ]

36. Kahneman D. Slovic P. y Tversky, A. (1982). Judgments Under Uncertainty. Heuristics And Biases. New York: Cambridge University Press.         [ Links ]

37. Kahneman, D. y Tversky, A. (1979). "Prospect Theory: An Analysis of Decision under Risk", Econometrica, 47(2): 263-291. Disponible en: http://www.jstor.org/stable/1914185. Consultado el 12 de septiembre de 2008.         [ Links ]

38. Le Menestrel, M. (2001). "A Process Approach to the Utility for Gambling". Theory and Decision, 50: 249-262.         [ Links ]

39. Lakatos, L. (2002). On Preferences for Fairness in Non Cooperative Game Theory. Disponible en: http://econ.core.hulesemeny/korosi/2002/LAL.PDF        [ Links ]

40. Loomes, G. y Sugden, R. (1986). Disappointment and dynamic consistency in choice under uncertainty. Review 0f Economic Studies, 53, 271-282.        [ Links ]

41. Loewenstein, G. y Elster 1. (Eds). (1992). Choice Over Time. New York: Russell Sage Foundation.         [ Links ]

42. Lucas, R. y Rapping, L. (1969). "Real Wages, Employment and Inflation". Journal of Political Economy, 77: 721-754.         [ Links ]

43. Luce R. D. and Krantz, D. H. (1971). "Conditional Expected Utility". Econometrica, 39: 253-271.         [ Links ]

44. Machina, M. (1982). "Expected Utility Analysis Without The Independence Axiom". Econometrica, 50(2): 277-323.         [ Links ]

45. Machina, M. (1989). "Dynamic Consistency And Non-Expected Utility Models Of Choice Under Uncertainty". Journal of Economic Literature, 27: 1622-1668.         [ Links ]

46. Markowitz, H. (1952). "The Utility of Wealth". Journal of Political Economy, 60: 151-158.         [ Links ]

47. Meehl P. P. (1954). Clinical versus statistical prediction: a theoretical analysis and a review of the evidence. Minneapolis: Minnesota University Press.         [ Links ]

48. Mehra, Rajnish; Edward C. Prescott (1985). "The Equity Premium: A Puzzle". Journal of Monetary Economics, 15: 145-161.         [ Links ]

49. Mosteller F. y Nogee P. (1951). "An Experimental Measurement of Utility". Journal of Political Economy, 59: 371-404.         [ Links ]

50. Pratt, 1., Raiffa, H. and Schlaifer, R. (1964). "The Foundations of Decision Under Uncertainty: An Elementary Exposition", Journal of the American Statistical Association, 59: 353-375.         [ Links ]

51. Prelec, D. (1998). "The Probability Weighting Function". Econometrica, 66 (3): 497 -527. Disponible en: http://www.jstor.org/stable/2998573.        [ Links ]

52. Rabin, M. (1997). "Bargaining Structure, Fairness and Efficiency". Berkeley: University of California.         [ Links ]

53. Samuelson, W. y Zeckhauser, R. (1988). "status quo Bias in Decision Making", Journal of Risk and Uncertainty, 1(1): 7-59.         [ Links ]

54. Santiago, J. (2003). El Papel de las Emociones en la Racionalidad del Agente Económico como respuesta a la TER. Tesis de grado con Mención Meritoria. Facultad de Ciencias Económicas, Universidad Nacional de Colombia, Bogotá.         [ Links ]

55. Savage, L. (1954). Foundations of statistics. New York: Wiley.         [ Links ]

56. Scitovsky, T. (1978). Frustraciones de la riqueza: la satisfacción humana y la insatisfacción de los consumidores. México: Fondo de Cultura Económica.         [ Links ]

57. Shubik, M. (1989). Game Theory in the Social Sciences. Massachusetts: MIT.         [ Links ]

58. Simon, H. (1989). Naturaleza y Límites de la Razón Humana. México: Fondo de Cultura Económica.         [ Links ]

59. Simon, H. (2006). Las ciencias de lo artificial. Barcelona: Editorial Comares.         [ Links ]

60. Sirvent, R. (1994). Tres ensayos sobre la teoría del arrepentimiento. Aplicación a las decisiones de seguro. Universidad de Alicante. Disponible en http://rua.ua.es/dspace/bitstream/10045/4065/1/Sirvent%20Boix%2c%20Ram%C3%B3n%20J.pdf.        [ Links ]

61. Shea, 1. (1995). "Myopia, Liquidity Constraints, and Aggregate Consumption: A Simple Test". Journal of Money, Credit, and Banking, 27: 798-805.         [ Links ]

62. Shea, J. (1995). Union Contracts and the Life-CyclelPermanent-Income Hypothesis. The American Economic Review, 85(1): 186-200. Disponible en: http://www.jstor.org/stable/2118003.         [ Links ]

63. Siegel, 1. y Thaler, R. (1997). "Anomalies: The Equity Premium Puzzle". Journal of Economic Perspectives, 11(1): 191-200.         [ Links ]

64. Starmer, C. (2000). "Source Developments In Non-Expected Utility Theory: The Hunt For A Descriptive Theory Of Choice Under Risk". Journal Of Economic Literature, 38(2): 332-382. Disponible en: http://www.jstor.org/stable/2565292. Consultado el 10 de julio de 2008.         [ Links ]

65. Strotz, R. (1956). "Myopia and Inconsistency in Dynamic Utility Maximization". Review of Economic Studies, 23(3): 165-180. Disponible en http://www.jstor.org/stable/2295722. Consultado el 12 de septiembre de 2008.         [ Links ]

66. Stutzer, A. Frey, B., M. (2006). "What Happiness Research Can Tell Us About Self-Control Problems And Utility Misprediction". Working Paper Series, 267. Institute For Empirical Research In Economics.University Of Zurich, Disponible en: http://www.iew.uzh.ch/index.html.        [ Links ]

67. Suppes, P. (1961). "Behavioristic Foundations of Utility". Econometrica, 29(2): 186-202. Disponible en: http://www.jstor.org/stable/1909288. Consultado el 12 de septiembre de 2008.         [ Links ]

68. Thaler, R. (1980). "Toward a Positive Theory of Consumer Choice". Economic Behavior and Organization, 1 :39-60.         [ Links ]

69. Tversky, A. y Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin, 76, 105-110.         [ Links ]

70. Tversky, A. y Kahneman, D. (1992). "Advances in Prospect Theory: Cumulative Representation of Uncertainty". Journal of Risk and Uncertainty, 5(4): 297-323.         [ Links ]

71. Varian, H. (1992). Análisis Microeconómico. Barcelona: Antoni Bosch Editores.         [ Links ]

72. Varian, H. (1994). Microeconomía Intermedia. Barcelona: Antoni Bosch Editores.        [ Links ]

73. Von Newmann, J. y Morgenstem, O. (1944). Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.         [ Links ]

74. Weber, M. (1998). "The Resilience ofthe Allais Paradox". Ethics, 109(1): 94-118. Disponible en: http://www.jstor.org/stable/2989509.         [ Links ]

75. Wakker, P., Chateauneuf, A. (1999). "An Axiomatization of Cumulative Prospect Theory for Decision Under Risk". Journal 0f Risk and Uncertainty, 18(2): 137- 145.         [ Links ]

76. Zeckhauser, R., Keeney, R., Sebenius, J., (Eds.). (1996). "Wise Choices. Decisions, Games And Negotiations". Boston, Massachusetts: Harvard Business School Press.         [ Links ]