Services on Demand
Journal
Article
Indicators
Related links
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.28 no.51 Bogotá July/Dec. 2009
EL MERCADO DE INSUMOS: UNA MIRADA DESDE EL COMPORTAMIENTO ESTRATÉGICO DE LAS FIRMAS
Juan Pablo Herrera Saavedra*
* Magister en Ciencias Económica. Profesor de la Universidad Javeriana y Universidad Externado de Colombia y actual asesor del Despacho del Superintendente de Industria y Comercio. E-mail: jpherrera@javeriana.edu.co. Dirección de correspondencia: Carrera 13 No. 27 - 00, piso 10 (Bogotá, Colombia).
El autor agradece las recomendaciones de los evaluadores anónimos de la Revista Cuadernos de Economía, las sugerencias de los profesores Carlos Andrés Álvarez, Edgar Bejarano y Adriana Peña en el Seminario Permanente de la Escuela de Economía de la Universidad Nacional de Colombia y los comentarios metodológicos del profesor Edgar Villa.
Este artículo fue recibido el 17 de febrero de 2009 y su publicación aprobada el 31 de agosto de 2009.
Resumen
El análisis del mercado de factores no es un tema usual en los cursos convencionales de microeconomía y cuando se aborda no se explican las motivaciones de las firmas al momento de tomar su decisión de compra de insumos. En contraste, se presentan amplias discusiones dirigidas a interpretar mecanismos de elección de las empresas en la producción y comercialización de bienes, en contextos oligopólicos y monopólicos. Este trabajo propone una reflexión del problema, a partir de instrumentos similares a los utilizados habitualmente para entender las motivaciones de una firma cuando determina sus decisiones estratégicas en mercados de bienes finales.
Palabras clave: economía industrial, teoría de juegos, estructuras de mercado. JEL: D40, D43, D49.
Abstract
The analysis of the input markets is a not usual topic in a standard course of microeconomics and there is no explanation about the decisions of the firms when they buy in the input market. In contrast, there are different approaches to explain mechanisms of choice of the firm in the production and commercialization of final goods in oligopolistic and monopolistic context. This note proposes a reflection of the problem using conventionally used tools to understand the firm in the market of final goods.
Key words: industrial economics, game theory, market structure. JEL: D40, D43, D49.
Résumé
L´analyse du marché de facteurs n´est pas un sujet habituel aux cours conventionnels de microéconomie et lorsque la question des choix des firmes est abordée, leur décision concernant l´achat de matières premières n´est jamais traitée explicitement. Par contre, il existe de vastes discussions à propos des mécanismes d´élection des entreprises dans la production et la commercialisation de biens finaux, dans des contextes oligopolistiques et monopolistiques. Ce travail propose une réflexion du problème, à partir des instruments similaires à ceux qui sont utilisés conventionnellement pour comprendre les motivations d´une firme au moment de déterminer ses choix stratégiques dans des marchés de biens finaux.
Mot clés : économie industrielle, théorie de jeux, structures de marché. JEL : D40, D43, D49.
El análisis del mercado de factores es un tema que en muchas discusiones convencionales de microeconomía se pasa por alto y la explicación sobre las motivaciones de las firmas a la hora de tomar la decisión de compra de insumos para los procesos productivos no es profunda. En contraste, se presentan consideraciones que van dirigidas a especificar mecanismos de elección de las firmas en la producción y comercialización de bienes en contextos oligopólicos y monopólicos. El artículo propone una reflexión en torno al problema a partir de un instrumento similar al utilizado habitualmente para entender las motivaciones de una firma a la hora de tomar decisiones estratégicas en mercados de bienes finales.
El documento consta de cinco secciones. La primera está dedicada a realizar una revisión de la literatura sobre el tema. En la segunda se presenta un modelo de monopsonio. La tercera parte está dedicada a la presentación de un oligopsonio en el cual cada una de las firmas participantes elige simultáneamente sobre cantidades de compra en el mercado de insumos. En el cuarto apartado se presenta un modelo líder seguidor en mercados oligopsónicos. En el quinto segmento presenta un modelo de competencia vía precios en el mercado de insumos. Y la séptima sección se dedica a las consideraciones finales.
REVISIÓN DE LA LITERATURA
A diferencia de la literatura relacionada con imperfecciones de mercado de bienes finales en los cuales se alude en muchos casos a monopolio y oligopolio, y sobre los cuales abundan trabajos teóricos y aplicados en economía, aquellos esfuerzos relacionados con el mercado de factores contrastan por su escasez.
Para Morgenstern (1948) la prioridad de analizar imperfecciones de mercado como el oligopolio y monopolio bajo herramientas de teoría de juegos daba cuenta de la poca importancia que el mercado de factores tenía como punto de referencia analítica. Sin embargo, tan solo se encuentra en su trabajo una breve referencia a oligopsonio como caso simétrico al oligopolio1.
Una reflexión interesante que vale la pena citar, es precisamente el trabajo de Thornton (2004) quien a través de una reflexión histórica muy interesante analiza los orígenes de los términos oligopsonio y monopsonio, concluyendo que el primero se remonta al año 1943 cuando fue utilizado por primera vez por Ronald Walker. Por su parte el término monopsonio fue implementado por Hallward en una conversación con Joan Robinson.
De otra parte, la necesidad e importancia de analizar a grandes compradores y sus connotaciones jurídicas y económicas en el mercado son abordadas por Dirlam y Kahn (1952). En su trabajo se analiza el caso de A&P y se muestran los límites de las leyes antitrust vigentes en la época, frente a los requerimientos efectivos que promueven la competencia en la industria. En su reflexión se realiza una descripción detallada del poder que puede tener el gran comprador en un mercado.
Por su parte, Lowry y Winfrey (1974) analizan la industria norteamericana de papel y partiendo de la premisa de la existencia de escasa literatura disponible que permitiera analizar el mercado de insumos, proponen la presencia de curvas de costos no suaves con discontinuidades. Ésta es distinta a la esperada curva de costos en forma de U que caracteriza habitualmente a los mercados cuando existe cierto grado de concentración en la compra de producto, traducido esto en oligopsonios.
Link y Landon (1975) analizaron los efectos del monopsonio sobre el nivel de salarios de las enfermeras que ofrecían su trabajo en los hospitales. Como resultado encuentran que el salario se ve seriamente afectado en aquellas zonas en donde los niveles de movilidad son restringidos y las exigencias de preparación son altas. De esta forma, los autores justifican la presencia de sindicatos como una alternativa para mitigar este impacto en el mercado laboral.
Just y Chern (1980) desarrollan un test empírico para verificar la presencia de poder de mercado. Para el efecto simulan un shock exógeno sobre el mercado relevante y analizan sus efectos. El test es aplicado a la industria procesadora de tomate en California en los años sesenta. Los resultados son consistentes con la teoría del modelo de la firma dominante fijadora de precios desarrollado por los autores.
En la misma dirección, el trabajo de Durham y Sexton (1992) analiza el mercado de tomates a partir de lo que los autores denominan Nuevos Modelos de Organización Industrial Empírica cuyo argumento fundamental, simétrico a las aproximaciones convencionales de organización industrial en oligopolio, corresponde al análisis de la oferta residual. Luego de exponer el modelo teórico y llegar a especificar los determinantes de la oferta residual de la industria y de cada firma procesadora de tomate que compra las cosechas, los autores realizan un ejercicio econométrico en el cual utilizan los datos semanales de producción de tomate en 1989 en las diferentes regiones del estado de California. La hipótesis fundamental a verificar se refiere a si las firmas procesadores de tomate en California pueden ejercer poder de mercado en las regiones cercanas a sus plantas de procesamiento. Los resultados muestran que su control sobre el mercado es limitado a diferencia de lo encontrado por Just y Chern (1980). En particular, los autores esgrimen la ausencia de una única firma procesadora de tomate como líder en el mercado y la presencia de asociaciones de cultivadores de tomate que han permanecido sin grandes modificaciones por más de 20 años. Así, el mecanismo de competencia interregional en el período investigado es mayor que el percibido 15 años atrás.
En un sector diferente Muth y Wohlgenant (1999) desarrollan un modelo para medir el grado de poder oligopsónico presente en la industria de empaquetamiento de carne. Utilizando un modelo de proporciones variables y una aplicación del teorema de la envolvente, los autores muestran que la relación entre el valor del producto marginal y el costo marginal del factor pueden ser definidos sobre los precios de insumos no especializados más que sobre sus correspondientes cantidades –estas últimas en muchos casos, difíciles de cuantificar e introducir en un modelo econométrico. En el período comprendido entre 1967 y 1993, y a partir de información tomada de USDA´s Meats Year Book y Livestock and Meat Statistics los autores no encuentran evidencia estadística de la presencia de poder de oligopsonio.
Otro trabajo que vale la pena citar en esta breve revisión de la literatura es el de Kallio (2001), quien propone un modelo de oligopsonio para entender la industria maderera en Finlandia. El autor considera dos tipos de firmas: unas extraen pulpa (insumo de la industria del papel) y otras extraen tanto pulpa como trozos de madera para aserrar. A través de la especificación del modelo, el autor muestra cómo es posible pensar en mecanismos de transmisión vía precios, entre los dos productos finales, dependiendo del grado de concentración que exista en uno u otro sector. En particular, para Finlandia, el autor muestra que el mercado de bloques de madera es menos concentrado desde el lado de la oferta que el mercado de pulpa. A su vez, encuentra que hay indicios de que la capacidad de producción de pulpa ha alcanzado los límites de su crecimiento potencial en el país. La principal lección del trabajo es que ante la imperfección de mercado observada, mercados integrados de los dos productos analizados resultarían ser menos ineficientes que aquellos que son completamente fragmentados.
El trabajo de Requillart, Simioni y Varela (2008) realizado en Francia para el caso del tomate, intenta analizar bajo un esquema oligopsonista el mecanismo de transmisión existente en la formación del precio de venta a lo largo de las cadenas productivas agrícolas. El análisis se basa en datos de consumo final, y en precios de producción y de venta al público de dos variedades de tomate en Francia: tomate redondo y tomate uva. Se utiliza un modelo estructural compuesto por un sistema de ecuaciones de demanda, de oferta y de precios. Estas últimas incluyen términos que representan el poder de mercado del sector de intermediarios. Se muestra que la elasticidad de la demanda varía durante el año y, como argumento central, que el sector intermediario sólo ejerce un poder moderado de mercado, que disminuye a lo largo del tiempo en Francia. El poder de compra produce efectos que se estiman entre 1,2% y 4,5%, en el transcurso del año.
Finalmente, el trabajo de Gabszewicz y Zanaj (2006), propone una reflexión en torno a la manera cómo se articulan diferentes mercados de insumos y bienes finales, para empresas que se encuentran en una misma cadena productiva (mercados sucesivos), en función del tipo de tecnología que permite caracterizar al grupo de firmas que participan en cada mercado. Así, los autores muestran que, bajo rendimientos decrecientes a escala y libre entrada de empresas al mercado, el proceso de formación de precio del insumo no lleva a que éste se ajuste a su costo marginal, como si sucede con rendimientos constantes a escala. De igual manera, analizan los impactos en el mercado ante la presencia de acuerdos de colusión en el mercado de bienes finales, asumiendo una función de costos determinada endógenamente dentro del modelo. Su agenda de investigación con respecto a esta temática, deja entrever lo relevante del estudio del comportamiento estratégico al interior de los mercados sucesivos y la intencionalidad de interiorizar cada uno de los componentes del modelo en aras de tener mayor claridad acerca de la identificación del equilibrio de la industria.
Como se observa, la literatura en torno a estos temas es menos amplia que la relacionada con el monopolio y el oligopolio, y la agenda de investigación aún sigue abierta. Por esta razón a continuación se realiza un ejercicio expositivo que intenta entender el problema teórico sugerido, a través de herramientas convencionales de teoría de juegos buscando elementos simétricos a las presentaciones habituales propuestas por Shy (1996) y Cabral (2000) en sus textos de Organización Industrial cuando se refieren a mercados donde hay algún grado de poder de mercado desde la oferta.
A lo largo de este artículo, se asumirá que las empresas participantes tienen rendimientos constantes a escala, tomando como exógeno el proceso de formación de precios en el mercado de bienes finales. No obstante, antes de iniciar con la presentación, el lector deberá tener muy presente que todos los resultados de equilibrio de la industria de cada uno de los modelos presentados están supeditados a esta restricción y que su ante el debilitamiento de los supuestos señalados debe hacer parte de la discusión.
MONOPSONIO
En adelante se supondrá una curva de oferta que cuenta con las siguientes características2 :

En este caso w corresponde al precio por unidad de insumo, z a la cantidad de insumo demandado, α es el precio mínimo al que se estaría dispuesto a ofertar el insumo en el mercado y β el efecto que sobre el precio de venta del insumo tiene el deseo de compra de una unidad adicional de dicho bien en el mercado.
De otro lado, se asume que el ingreso asociado a la compra del insumo para la firma está dado por:

Esta expresión sugiere por simplicidad que el ingreso que percibe la firma monopsonista por la compra y posterior uso del insumo y venta del producto será de forma lineal3. De esta forma, el problema del monopsonista estará dado por la siguiente expresión:

0 de forma equivalente,

La condición de primer orden permitirá encontrar la demanda del insumo que realizará el monopsonista, denotada en adelante como z m, junto con el precio que se fijaría en el mercado (w m) y los beneficios del monopsonista (π m):
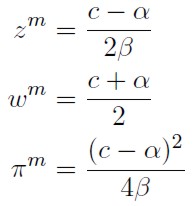
En esta expresión se aprecia que el precio que se fija en este mercado resulta ser el promedio simple entre el precio mínimo al que se está dispuesto a ofrecer el insumo y el ingreso marginal que percibiría el monopsonista al usar el insumo4. De igual forma, puede observarse que el beneficio que percibiría el monopsonista sería estrictamente positivo y la cantidad a ofrecer estaría directamente asociada con el ingreso que percibe el monopsonista en el mercado e inversamente asociada con el precio mínimo al que se ofrece el producto y el parámetro de sensibilidad de la oferta.
El siguiente gráfico ilustra los argumentos esbozados:

En la Gráfica 1 se aprecia cómo el precio que se fijaría en el mercado monopsónico es significativamente más bajo que aquél que sería establecido en un mercado competitivo (c), que correspondería precisamente a un nivel equivalente al ingreso marginal, que le representaría a esta firma la contratación de la cantidad de insumo. A su vez, en la gráfica se hace alusión al gasto marginal asociado a la compra del insumo; éste es obtenido a partir de la condición de primer orden propuesta en líneas anteriores y es definido como Gmg = α + 2βz.
OLIGOPSONIO SIMULTÁNEO
Dos firmas homogéneas
Considere ahora un par de firmas que enfrenta las mismas consideraciones de oferta en el mercado del insumo z que las descritas en la sección anterior.
Esto es:

Pero ahora, z = z1 + z2. Cada una de las firmas percibe ingresos por la ompra y posterior uso del insumo; por simplicidad se asume que I1 (z*) = I2 (z*). Así el problema de cada una de las firmas será:

O de manera equivalente:

La condición de primer orden asociada al problema permite encontrar las funciones de mejor respuesta de cada una de las firmas:

De esta manera, igualando cada una de las funciones de reacción, es posible encontrar el equilibrio de Nash asociado a este problema; esto es, la mejor respuesta que podría elegir una firma dada la mejor respuesta de su competidor. Obsérvese en este punto que el resultado en este mercado resultaría ser simétrico al mercado de bienes finales tipo Cournot. De esta manera en adelante las cantidades, precios y beneficios de equilibrio serán notados por un supra índice cr para evitar confusiones con los otros equilibrios que se determinan en este documento:

Es decir, en el equilibrio se compraría en el mercado un nivel de insumo correspondiente a:

El precio al que se compraría el insumo será igual a:

Como se observa, el precio fijado en el equilibrio termina siendo un promedio ponderado entre el precio mínimo al que los oferentes están dispuestos a comprar el producto y el ingreso marginal que le genera a cada una de las firmas dicho insumo. Dicho precio resulta ser estrictamente menor que el ingreso marginal (c) y estrictamente mayor al precio al cual un monopsonista realizaría su compra en el mercado (w m). Las ganancias percibidas por cada firma serán:

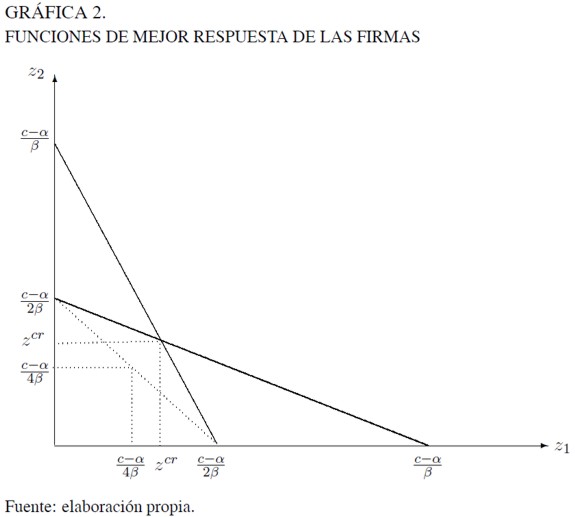
La Gráfica 2 ilustra la relación de sustituibilidad existente en las decisiones de compra de insumos. La intuición detrás de este mecanismo resulta ser relativamente simple. A mayor presión de compra por parte del competidor se genera un alza en el precio de mercado que desestimula la compra del insumo; por tal razón, lo mejor que puede hacer cada una de las firmas es ajustar a la baja su decisión de compra en la medida en que el competidor decida incrementar su demanda.
De igual forma, se aprecia en la gráfica un segmento de recta que une dos interceptos asociados a cada una de las funciones de mejor respuesta de las firmas. En cada uno de los puntos de dicha recta se satisface que z1 + z2 = c - α / 2β , es decir, en el agregado se demandaría justamente la cantidad de monopsonio, dando así las posibilidades para fijar el precio más bajo de compra de insumos en el mercado. En otras palabras, cada una de las combinaciones citadas serían puntos de un potencial acuerdo entre las firmas que compran el insumo analizado. De todos ellos y asumiendo homegeneidad de las firmas, el más creíble correspondería a aquel en el que cada una de las firmas se comprometiese a comprar el 50% de la cantidad de monopsonio, esto es c - α / 2β5.
Múltiples firmas homogéneas
Considerando ahora un número finito de firmas homogéneas (N ), cada una de ellas con las características expuestas en la sección anterior, se podría afirmar que:

siendo zi la cantidad que compra la firma i en el mercado de insumos.
Tal como se ilustró en el apartado anterior, se asume que cada una de las firmas, actuando estratégicamente, maximiza sus beneficios. La función que enfrenta cada firma al maximizar los beneficios estará dada por:

Siendo z _ i un vector de la forma ( z1, . . . , zi - 1, zi + 1, .. , zN ).
De esta manera, existen N funciones de mejor respuesta de la forma descrita y el equilibrio de Nash asociado al problema podría determinarse de acuerdo con el siguiente argumento.
Puede mostrarse que al ser idéntica la tecnología de cada una de las firmas que producen un único bien, el punto fijo de las funciones de mejor respuesta de cada una de las firmas estará dado por:

Así, la función de mejor respuesta puede escribirse de la siguiente manera:

De ésta es posible obtener el nivel de z _cr:

Por tanto, se tiene que la cantidad agregada del insumo será igual a:

El precio que se fijaría en el mercado de insumos correspondería a:

Finalmente, los beneficios que recibiría cada una de las firmas compradoras del insumo serán:

Con los resultados encontrados es posible determinar el efecto que podría generarse en el equilibrio al existir un número más grande de empresas comprando en el mercado de insumos. De esta forma se tiene que:

Se concluye entonces que a medida que se incrementa el número de firmas que compran insumos, el beneficio de cada una de ellas se reduce y la compra que puede realizar cada empresa de manera estratégica es cada vez menor; sin embargo, el precio aumenta al existir mayor presión desde la oferta, convergiendo asintóticamente a la solución competitiva.
Firmas heterogéneas
Ahora si se asume que las firmas perciben ingresos diferentes asociados a la contratación del insumo, entonces se tiene que:

De esta forma, el problema de cada firma que compra insumos será:

La condición de primer orden asociada al problema permite encontrar las funciones de mejor respuesta de cada una de las firmas:

De esta manera, igualando cada una de las funciones de mejor respuesta, es posible encontrar el equilibrio de Nash asociado a este problema; esto es, la mejor respuesta que podría elegir una firma dada la mejor respuesta de su competidor. Así se obtiene que6:

A su vez, la cantidad de producción agregada será igual a:

Por tanto, el precio que se fijaría en el mercado sería igual a:

En otras palabras, el precio de mercado resultaría ser un promedio simple entre el precio mínimo al que se ofrecería el insumo y cada uno de los ingresos marginales que perciben las firmas con la compra del insumo.
OLIGOPSONIO SECUENCIAL (MODELO LÍDER SEGUIDOR)
Considere ahora dos firmas con ingresos homogéneos por concepto de contratación de insumos, tal que una de ellas antecede en la elección del volumen de compra a su competidor. De esta forma, se tiene un juego secuencial en el que la firma que se anticipa es la firma líder y quien elige en un siguiente momento es la firma seguidora. Si las firmas obtienen sus ganancias una vez se haya fijado el precio de mercado al final del proceso de elección, entonces pueden hacerse dos consideraciones importantes:
-
El conjunto de información de cada una de las firmas compradoras del insumo es significativamente diferente. La firma seguidora dispone de la historia de lo sucedido en el período inmediatamente anterior.
-
A pesar de que la firma seguidora dispone de mayor información, su comportamiento está completamente condicionado y, como se mostrará, restringido por la decisión de la firma que antecede su elección.
La siguiente figura ilustra la representación extensiva del juego propuesto.

Teniendo en cuenta que el juego tiene información perfecta y completa, es posible abordar el problema utilizando el algoritmo de inducción hacia atrás para obtener el Equilibrio de Nash Perfecto en Subjuegos (ENPS).
Asumiendo una estructura de oferta similar a la de secciones anteriores, el problema de la firma seguidora podrá expresarse de la siguiente forma:

O de manera equivalente como:

La condición de primer orden asociada al problema permite encontrar la función de mejor respuesta de la firma seguidora:

Si la firma líder es capaz de generar esta conjetura sobre el comportamiento de la firma seguidora, incorporará esta reacción para determinar su elección, enfrentando el siguiente problema:

Lo que sería igual a resolver el siguiente problema de optimización:

La condición de primer orden asociada al problema permite determinar la demanda del insumo de la firma líder.

De esta manera se tiene que:

Reemplazando lo anterior en la función de mejor respuesta de la firma seguidora permite obtener:

Expresado de otra manera, la firma líder termina comprando el 66,6% del total del insumo, mientras que la firma seguidora apenas logra comprar el 33,3%.
Por consiguiente, la cantidad total de mercado será:

Y el precio de mercado al cual se concretará la transacción será:

Obsérvese que el precio cobrado es un promedio ponderado entre el precio mínimo al que se ofrece el insumo y el ingreso marginal que le aporta a la firma la contratación del mismo, en una proporción 1 a 3.
Se observa claramente que el precio caracterizado en esta sección resultaría ser mayor que el encontrado cuando las firmas homogéneas compiten en el mercado de insumos simultáneamente, el cual es a su vez estrictamente mayor que el precio de mercado bajo un esquema de monopsonio. Es decir, teniendo en cuenta los casos descritos en el documento, el precio del juego en forma extensiva resultaría ser el segundo más alto susceptible de fijarse, luego de la situación competitiva.
COMPETENCIA VÍA PRECIOS
Para finalizar esta breve reflexión del mercado de insumos, esta sección presenta los efectos que podrían darse en el mecanismo de competencia si las firmas decidieran enfrentarse vía precios, esto es, ofrecer el precio más atractivo para convencer a los oferentes de llevarse la cantidad producida. Si los oferentes del insumo son racionales y en principio no existen límites de compra de dicho insumo por parte de las empresas interesadas en la compra, es de esperarse que la venta se realice a quien ofrezca un precio por unidad más alto, excluyendo a aquel competidor que haya realizado la oferta más baja en el mercado. De esta forma, la oferta del insumo estará dada por la siguiente expresión:

Para abordar el problema, y únicamente por razones ilustrativas del desarrollo del modelo, se intentará precisar la mejor respuesta que cada competidor tendría ante los posible escenarios de interacción en el que se encuentre con su rival. Inicialmente, se analiza qué sucedería si la empresa i lograra ser monopsonista, es decir, si la firma i ofrece un precio superior al ofertado por su competidor, la firma j, en la compra del insumo. Lo que se expresa como: wi > wj > α.
En este caso los beneficios de la firma estarían dados por la siguiente expresión:

Reescrito de otra manera, esta expresión será:

Obsérvese que esta función resulta ser una parábola que abre hacia abajo. Para determinar su punto crítico, las condiciones de primer orden estarán dadas por la siguiente expresión:

En la cual w*i = c + α / 2 y π*i = (c + α)2 / 4 - αc. A su vez, es importante notar que πi (c) = πi (α) = 0. La Gráfica 3 ilustra el resultado encontrado.

No obstante, en el gráfico se representa la capacidad de la firma i de fijar un precio superior al de su competidor, lo cual corresponde a un único caso dentro de todos los escenarios posibles para el oligopsonista. Si la decisión efectiva de su competidor resultara ser un precio por encima del que ha decidido la i-ésima firma, ésta sencillamente no podría realizar ninguna compra y sus beneficios serían cero. Si coincidieran sus elecciones en precios podría pensarse en un repartición del mercado de forma equitativa7. De la misma forma, si la oferta es tan baja que no resulta atractiva para los oferentes (wi < α ), entonces sus beneficios serán nulos ante la imposibilidad de compra. Así, la verdadera función de beneficios para cada firma resultaría ser una función discontinua, dada por la siguiente condición:

De esta manera, asumiendo información completa y teniendo en cuenta que cada firma se enfrentaría a un proceso de interacción en el cual los pagos se rigen por la función de beneficios descrita, es posible determinar la correspondencia de mejor respuesta de cada firma ante las posibles acciones de su rival, tal como se presenta a continuación.
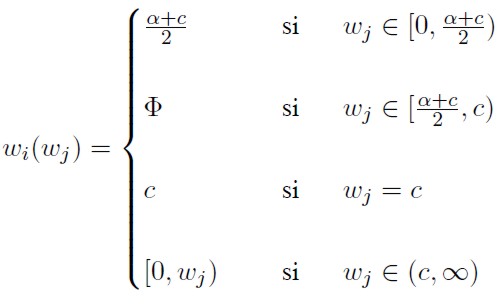
Como se observa en la Gráfico 5 el único punto común de las dos correspondencias será wi = wj = c; es decir, el único equilibrio de Nash asociado a este mecanismo de competencia es un precio fijado por cada firma, equivalente al ingreso marginal que generaría la compra de cada unidad de insumo (c). Este resultado indicaría que ante una potencial guerra de precios, si existe información completa en el mercado, el precio que llegaría a ser la mejor respuesta de cada firma ante el comportamiento óptimo de su competidor sería c. Si se fija este precio, no existirán incentivos para desviarse unilateralmente de él, por parte de alguna de las compañías.

CONSIDERACIONES FINALES
El presente documento ha mostrado varios instrumentos mediante los cuales es posible entender la elección que realizan las empresas en la compra de insumos en un mercado. Más allá de describir los determinantes de la oferta y hacer un ejercicio aplicado, como la mayoría de los trabajos referenciados al inicio del artículo, el ejercicio se ha concentrado en determinar la manera cómo las empresas tomarían sus decisiones de compra estratégicamente en el mercado, bajo distintos escenarios de competencia.
En particular, asumiendo ingresos marginales constantes asociados al uso que pueda representar la cantidad de insumo demandado, se puede concluir que el precio más bajo que una firmamonopsonista fijaría indirectamente en el mercado sería un promedio simple entre el nivel de ingreso marginal que percibiría por el uso del insumo y el precio mínimo al cual los productores sacarían el producto al mercado.
A su vez, el precio que se fijaría como resultado de la interacción de duopsonistas que actúan estratégica y competitivamente en el mercado, sería equivalente a un promedio ponderado entre los dos mismos argumentos citados en el caso del monopsonista; la diferencia es que en este caso se le daría una ponderación de 33,3% al precio mínimo y de 66,6% al ingreso marginal.
Finalmente, y en orden ascendente, el precio que se fijaría en un escenario de duopsonio en un contexto líder-seguidor sería equivalente a un promedio ponderado en el cual el 25% es asignado al precio mínimo y el 75% restante al ingreso marginal.
El precio competitivo corresponderá al equivalente al ingreso marginal percibido a futuro por las firmas compradoras de insumo, el cual representa a su vez el único equilibrio de Nash en estrategias puras que alcanzarían las firmas, ante una eventual guerra de precios.
Como agenda de investigación, queda por explorar las relaciones que podrían establecerse entre los mercados de bienes finales y de insumos. Tal como se señaló en el documento, para efectos de la determinación del equilibrio de la industria en todos los casos, se asumió un proceso de formación de precios de bienes finales exógeno, con firmas que presentan rendimientos constantes a escala. El disponer de un modelo que permita entender el comportamiento estratégico de empresas que participan en mercados sucesivos, minimizando las consideraciones ad-hoc que deban ser impuestas, es quizás uno de los retos principales dentro de esta reflexión.
NOTAS AL PIE
1 Ver Morgenstern (1948,12).
2 Se supone implícitamente que, de existir multiplicidad de agentes oferentes de insumos, cada uno de ellos asumirá como dado el precio al que puede vender su producto. La función inversa de demanda reflejará la forma como se determina el precio de mercado en función de las decisiones que se puedan producir desde la compra.
3 El supuesto detrás de este argumento es que la firma compradora del insumo tiene un proceso que exhibe rendimientos constantes a escala. En este caso, el parámetro c representa información del precio del bien (o bienes finales) que se genera en el mercado junto con parámetros tecnológicos que permiten producir dicho bien y por lo cual se remunera el insumo
4 Dicho ingreso marginal resultaría ser en un mercado competitivo el precio que sería cobrado a la firma compradora del insumo, siendo entonces w m estrictamente inferior a dicho precio.
5 Es importante aclarar que la solución sugerida no es estable ya que al ser un resultado de un proceso de colusión, existen todos los incentivos a comprometer al competidor al acuerdo e inmediatamente desviarse del mismo. Al no existir ningún mecanismo de penalización, el acuerdo es una solución inestable.
6 Es importante señalar que la solución será interior asumiendo que 2ci - cj > α y que ci + cj > 2α.
7 Dada la simetría de las firmas, un posible escenario sería la repartición simétrica en el proceso de compra insumos.
REFERENCIAS BIBLIOGRÁFICAS
1. Arévalo, J. y Monsalve, S. (eds.) (2007). Un curso de teoría de juegos clásica. Bogotá: Universidad Externado de Colombia. [ Links ]
2. Bakken, H. y Muller, W. F. (1952). Oligopsony in the Tobacco Industry. Land Economics, 28(2), 132-146. [ Links ]
3. Cabral, L. (2000). An Introduction to Industrial Organization. Cambridge, MA: MIT Press. [ Links ]
4. Cheng, Z. y Lent, R. (1992). Supply Analysis in an OligopsonyModel. American Journal of Agricultural Economics, 74(4), 973-979. [ Links ]
5. Devadoss, S. y Song, W. (2006). Oligosony Distorsions and Welfare Implications of Trade. Review of International Economics, 14(3), 452-465. [ Links ]
6. Dirlam, J. y Kahn, A. (1952). Anitrust Law and the Big Buyer. The Journal of Political Economy, 60(2), 118-132. [ Links ]
7. Durham, C. y Sexton, R. (1992). Oligopsony Potential in Agriculture: Residual Supply Estimation in California´s Processing Tomato Market. American Journal of Agricultural Economics, 74(4), 962-972. [ Links ]
8. Gabszewicz, J. y Zanaj, S. (2006). Competition in Succesive Markets: Entry and Mergers. CORE Discussion Papers 2006097. Lovaina: Université Catholique de Louvain, Center for Operations Research and Econometrics (CORE). [ Links ]
9. Just, R. y Chern, W. (1980). Technology and Oligopsony. The Bell Journal of Economics, 11(2), 584-602. [ Links ]
10. Kallio, M. (2001). Interdependence of the Sawlog, Pulpwood and Sawmill Chip Markets: an Oligopsony Model with an Application to Finland. Silva Fennica, 35(2), 229-243. [ Links ]
11. Link, C. y Landon, J. (1975). Monopsony and Union Power in the Market for Nurses. Southern Economic Journal, 41(4), 649-659. [ Links ]
12. Lowry, T. y Winfrey, J. (1974). The Kinked Cost Curve and the Dual Resource Base under Oligosony in the Pulp and Paper Industry. Land Economics, 50(2), 185-192. [ Links ]
13. Morgenstern, O. (1948). Oligopoly, Monopolistic Competition and the Theory of Games. The American Economic Review, 38(2), 10-18. [ Links ]
14. Muth, M. y Wohlgenant, M. (1999). Measuring the Degree of Oligopsony Power in the Beef Packing Industry in the Abscence of Marketing Input Quantity Data. Journal of Agricultural and Resource Economics, 24(2), 299-312. [ Links ]
15. Requillart, V., Simioni, M. y Varela, L. (2008). Imperfect Competition in the Fresh Tomato Industry. IDEI Working Papers 498. Toulouse: Institut d´Économie Industrielle (IDEI). [ Links ]
16. Shy, O. (1996). Industrial Organization. Cambridge, MA: MIT Press. Thornton, R. (2004). Retrospectives. How Joan Robinson and B. L. Hallward named Monopsony. The Journal of Economics Perspectives, 18(2), 257-261. [ Links ]














