Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.29 no.53 Bogotá July/Dec. 2010
ARE THERE GOODWIN EMPLOYMENT-DISTRIBUTION CYCLES? INTERNATIONAL EMPIRICAL EVIDENCE
Mario García Molina*
Eleonora Herrera Medina**
* Economics Ph.D. currently occupies the position of professor of the Economic Sciences Faculty of the Universidad Nacional de Colombia. and the Economy Faculty of the Universidad Externado de Colombia. Mailing address: Cra 30 N. 45-03. Facultad de Ciencias Económicas, edificio 311, oficina 306, Universidad Nacional de Colombia, (Bogotá, Colombia). E-mail: mgarciamo@unal.edu.co.
** Masters degree in Economics. Currently occupies the position of director of the Centre of Economic Studies and Analyses of the Universidad Antonio Nariño. Mailing address: Kra 3 este N. 47 A - 15, bloque 4, cuarto piso (Bogotá, Colombia). E-mail: director.ceae@uan.edu.co.
We are grateful to Heinz Kurz and Alvaro Moreno for comments. This article was received on October 28, 2009 and his publication approved on April 23, 2010.
Resumen
El modelo depredador-presa de Goodwin predice ciclos en el sentido del reloj en el plano empleo-distribución. Se presenta evidencia cualitativa de comportamiento no lineal para una muestra de 67 países, algunos con ciclos como los de Goodwin. Los centros estimados yacen por fuera de los ciclos observados. El tipo de ciclo (en el sentido del reloj, contrario o atípico) parece relacionarse con el tipo de capitalismo del país. Economías con capitalismo de mercado o europeo, y las economías en transición no presentan ciclos de demanda; los países en desarrollo con capitalismo mediterráneo no presentan ciclos de Goodwin.
Palabras clave: modelo depredador-presa; comportamiento no lineal; ciclos de demanda; ciclos de crecimiento. JEL: C10, E32, E19, O47.
Abstract
Goodwin´s predator-prey model predicts clockwise cycles in the employment–distribution space. Qualitative evidence is provided in favour of nonlinear dynamic behaviour for a sample of 67 countries, some of which have cycles similar to those predicted by the model. Predicted centres lie outside actual circles. The kind of cycle (clockwise, counter clockwise or atypical) appears to be related to the kind of capitalism of the country. Countries with Market or European capitalism, as well as transition economies, do not tend to have demand cycles; developing countries with a Mediterranean capitalism do not tend to have Goodwin cycles.
Key words: predator-prey model, non-linear dynamic behaviour, demand cycles, growth cycles. JEL: C10, E32, E19, O47.
Résumé
Le modèle prédateur-proie de Goodwin prédit des cycles dans le sens des aiguilles de la montre par rapport dans l´espace emploi-distribution. Ce papier propose de l évidence qualitative supportant un possible comportement dynamique non linéaire pour un échantillon de 67 pays, dont certains ont des cycles semblables à ceux prédits par le modèle. Le type de cycle (dans le sens des aiguilles d´une montre, inverse ou atypique) semble être rattaché au type de capitalisme du pays analysé. Les pays caractérisés par une forme de capitalisme de marché ou européen et les économies de transition n´évidence pas de tendance à avoir des cycles de demande; les pays en développement caractérisés par une forme de capitalisme méditerranéenne ne montre pas des cycles de type Goodwin.
Mots clés: modèle prédateur-proie, comportement dynamique non linéaire, cycles de demande, cycles de croissance. JEL : C10, E32, E19, O47.
Richard Goodwin´s (1967, 1972) model of the growth cycle attempted to show how accumulation takes a cyclical form due to the interaction of capitalists and workers in a Marxian way. This simple theoretical model of endogenous cycles has been further explored in several directions including the realism of its assumptions, its stability and possible generalizations (Goodwin et al, 1984); there has been less interest in performing empirical studies, with the exception of Atkinson (1969), Desai (1984) Solow (1990), Harvie (2000) and Moreno (2002). This literature has provided evidence on single countries or on a small number of them, the largest sample so far being 10 OECD countries in the case of Harvie (2000).
The aim of the article is to provide evidence about employment distribution cycles à la Goodwin for a larger number of countries at several levels of development.
The model´s central dynamics is a cyclical relationship between income shares and employment. This behaviour should underlie the dynamics of developed capitalist economies, but it should also at least partially explain the behaviour of developing capitalist countries. If this relationship holds, it should appear as a cycle in the scatterplots of the workers´ share against the employment rate. Furthermore, on a quantitative level, the model´s estimation of the cycle´s centre can be compared with the position of the actual centre of the cycle found for a country. Finally, Goodwin´s assumptions can be tested to check for their validity. The procedure of looking for qualitative and quantitative evidence and testing the assumptions was performed by Harvie (2000), who found not exactly a cycle but what looked like part of a cycle (around a quarter) for 10 OECD countries during the period between the late 1960´s and the mid 1990´s, which qualitatively supported the idea of a cycle. However, he also found that the estimated centres lay outside the actual cycles, while the assumptions were not justified, which meant that at a quantitative level the model was not adequate. Harvie´s methodology is used here for a larger number of countries at different levels of economic development in order to provide a better grasp of the extent to which the model holds empirically and to offer possible directions for future developments.
Section 1 presents the model. Section 2 provides evidence on whether there are cycles in the employment-distribution space from a sample of 67 countries with different levels of development. Section 3 discusses the evidence and concludes with suggestions for future study.
GOODWIN´S MODEL
Goodwin (1967, 1972) models the cyclical behaviour in the workers´ share of national income and the employment rate by means of the Lotka-Volterra predator-prey model (Lotka, 1956; Volterra, 1931a, 1931b, 1937). The model attempts to formally present Marx´s idea that the interaction between distribution and employment was at the root of capitalism´s booms and slumps.
Assuming a constant relation of "constant" (the value of the means of production) to "variable" (wages) capital, both constant and variable capital will grow until full employment of labour is reached. In the neighbourhood of full employment, real wages will rise (i.e. a real Phillips curve), but rising real wages reduce the rate of profits and thus dampen accumulation.
The lower rate of accumulation will engender unemployment, removing the disproportion between capital and exploitable labour-power. Real wages fall and accumulation picks up again.
Goodwin assumes two factors of production: capital and labour. All quantities are real and net. Labour productivity (α) and the labour force (n) grow at constant rates (equations 1 and 2). σ is the fixed capital output ratio (equation 3), which determines the employment level l (equation 4). k is the total stock of capital, q is real output, l is employment, w is the real wage, and u the workers´ share of national income (equation 5); υ is the employment rate (equation 6).
Capitalists are assumed to save and invest all their profits and workers to consume all their wages (equation 7). Finally, a linear real Phillips curve is assumed, i.e. real wages rise as employment increases (equation 8).
From equations (1)-(8) a pair of differential equations in the state variables u and ν can be obtained:
The solution of the model is a family of closed cycles around a centre, i.e., the economy comes back to the initial point and starts the cycle again.
Because this is a highly stylized model, it leaves out several aspects, which will be of importance in the empirical testing.
First, the length and the amplitude of the cycles are not clear. Scholars who have studied cycles and waves have identified superimposed cycles of different lengths. As regards to the short run, there are 1, 2, 3 and 5 year cycles (Zarnovitz, 1985); in the long run, there are (or may be) Juglar (7-11 years), Kuznetz (15-25 years) or Kondratiev (45-60 years) cycles (Schumpeter, 1954; Kondratieff and Stolper, 1935; Solomou, 1987). It is true that the length and amplitude of Goodwin cycles can be numerically determined from the equations, but there still remains a theoretical problem, for which Goodwin does not provide an explicit answer, as the assumptions of the model do not point in a definite direction.
On the one hand, the model assumes exogenous technical progress, which could be taken in favour of a short run interpretation, although at the time the model was built this was a standard assumption among many (neoclassical) growth theorists. On the other hand, the assumption of Say´s law points to a long run interpretation, as used in other growth models. Given these assumptions, it is no surprise that Goodwin cycles have been interpreted in different ways: Veneziani and Mohul (2006) see them as "short" cycles; while Harvey (2001), and Flaschel and Groh (1995) take them as "long" cycles.
Another point worth remembering is that the cycles discussed in the literature refer mainly to variables such as price and output. This is hardly surprising as long series were available for said variables. Kondratieff cycles, for instance, were originally developed mainly for prices and only later emphasized other variables. However, Goodwin´s model refers to the share of wages in the national income, and to the employment rate. Neither of these variables corresponds exactly to the ones in the other cycles already mentioned. Hence, there is a possibility for Goodwin cycles to have amplitudes or lengths that are not exactly those of other known cycles.
Finally, if a Goodwin model predicts clockwise cycles as a result of investment being led by profits, the economy may also be considered as being led by wages with counter clockwise cycles. The former are classical cycles, while the latter are Keynesian cycles. It is also possible to mix both, but the outcome will depend on the exact way they are combined. Dumenil and Levy (1999), for example, combined short-term Keynesian dynamics with a long-term classical model; another case was that of Canry (2005), who incorporated a Bhaduri-Marglin (1990) model within a Goodwin framework. The results of these models depend on the specificities of the equations, which in turn could be interpreted as reflecting the institutional environment of the model.
Another factor that has an effect on joint classical-Keynesian models is the way of dealing with Say´s law. Goodwin´s model assumes Say´s law, in the classical way, i.e. in the sense that capital always finds employment, not so labour. This means that there are no effective-demand problems, but at the same time the Keynesian part would imply a rejection of Say´s law. This problem will not be dealt with here, but should be kept in mind by studies dealing with mixed models.
¿ARE THERE DISTRIBUTION-EMPLOYMENT CYCLES?
Data were collected for 67 countries from different sources, including UN, IMF, the World Bank, central banks, national statistics offices, regional organizations, and databases from local universities. As the building of the cycles for single countries included local sources, there may be countries for which figures are not expressed in PPP exchange rates. As a result, comparisons among countries cannot be made in quantitative terms, although qualitative behaviour within a country can be established. This means, for instance, that with the data set it is not possible to say that a country´s cycle is twice wider than another´s, but it is possible to say that both are clockwise cycles.
With regard to quantitative evidence, the theoretical centres of the cycles lay outside of the cycles in all cases (an example is provided in Figure 1), as also found in Harvie (2000).

The assumption of a linear real Phillips curve was tested, and was not rejected for only thirty-nine of the countries (see table 1).

Note that twenty-one countries had the expected qualitative behaviour despite the Phillips curve not holding (see appendix 2 ). A particular problem of the real Phillips curve is that Goodwin assumes a linear version of it in order to obtain the Predator Prey equations. However, it would be more reasonable to believe that real wages would only increase near full employment, not before, which would suggest a non-linear version. Nevertheless, a more realistic version would make model building far too complicated. Still, previous empirical evidence on the procyclicality of real wages is neither general nor strong (Abraham and Haltiwanger, 1995).
It is well known (Veneziani and Mohun, 2006) that Goodwin´s model is structurally unstable, which means that even a small change in the model may affect its dynamics. As a result, before testing particular extensions of the model, the rather general question of whether the cycles predicted by the model actually exist should be studied first. Scatter plots of the share of wages against the employment rate were made for the 67 countries (see appendix 2). One problem that arises is that of the time span.
Consider the cycle shown in figure 2a. Did Goodwin refer to the long cycle that appears in the graph or to the shorter movements around this tendency? The series was smoothed by means of a Hodrick and Prescott filter with λ = 100 (this value is for annual data). The smoothed series and the residuals appear in figures 2b and 2c. If the Goodwin cycles were "short", they should appear in figure 2c, but there seems to be no cyclic behaviour there. Although there seem to be oscillations in the individual variables, they are not related in such a way as to create cycles in the employmentdistribution plane. In addition, the residuals of the Hodrick and Prescott filter are not autocorrelated. Thus, the cyclic behaviour should correspond only to figure 2b. The remaining graphs are those of the smoothed series. It should be noticed that the cycles found with this procedure are several decades long and seem to be long waves rather than business cycles. Goodwin (1987) actually developed a different model for long waves, but he focused there on the interaction between innovation and output and did not mention employment-distribution cycles. In the models on long waves, profits are emphasized over real wages or the share of labour (e.g. Enton and Poletayev, 1987). Sterman (1987) posed a cyclical relation between employment and real wages, although not between employment and the share of wages, and the relation was not the key argument. In any case, the actual evidence found in this study relates to the existence of employmentdistribution cycles, and it is too early to conclude what is the best model to fit the data.



The scatter plot results were widely diverse (see appendix 2). A group of twenty-six countries (Australia, Austria, Belgium, France, Germany, Italy, New Zealand, United Kingdom, United Sates, Bahrain, Estonia, India, Ireland, Jamaica, Japan, Kazakhstan, Kenya, Kyrgyz Republic, Moldova, Netherlands, Panama, Slovakia, Sri Lanka, Thailand, Tunisia and Zimbabwe) behaves in the way predicted by the model (e.g. figure 3).

A second group comprised of nine countries (Costa Rica, Honduras, Turkey, Armenia, Belarus, Iceland, Ecuador, Mexico and Paraguay), has a cycle in the opposite direction (e.g. figure 4), that is, they do not show evidence of profit squeeze but rather of Keynesian-like or demand-pushed cycles such as the one found by Barbosa-Filho and Taylor (2003) for the United States. And for a third group of thirty two countries (Algeria, Bolivia, Botswana, Brazil, Canada, Chile, Colombia, Czech Republic, Denmark, Finland, Greece, Hong Kong, Jordan, Kuwait, Luxembourg, Malta, Mauritius, Namibia, Norway, Peru, Poland, Portugal, Russian Federation, South Africa, South Korea, Spain, Sweden, Switzerland, Tanzania, Trinidad and Tobago, Ukraine and Venezuela) there is no evidence of a cycle (figure 5).


Notice that the results are not clearly related to the degree of development as measured by the 2005 World Bank estimation of per capita income (table 2). High income countries (i.e. those with GDP per capita greater than US$ 11,115 in 2005) behave either in the way predicted by Goodwin or in an atypical fashion, not in a demand cycle way; middle-income countries show all dynamics, either Goodwin, demand or atypical, although African, European and American countries tend to be atypical. The strongest tendencies seem to be for low-income countries to show Goodwin cycles and for demand cycles to appear mainly in middle-income countries.


A possible explanation for this diversity is that capitalism has evolved in several ways in different countries according to different kinds of institutions that affect capital accumulation, particularly but not exclusively, labour market institutions. As noted by Arrighi (1978) and more recently by Acemoglu et al (2001), institutional development may be linked to the pattern of population and migration. Another example of institutional diversity refers to the institutions regulating capital. A few countries (mainly Anglo-Saxon ones) rely on more atomistic shareholders and individual firms. In contrast, most other countries have business groups with controlling shareholders playing a much more important role than that suggested in typical textbooks (La Porta et al, 1999). In general, the characteristics of institutions might help to classify the different kinds of capitalism and help to understand diversity in the relationship between distribution and employment.
In order to take institutional diversity into account, the classification employed by Amable (2005) was used. This author suggests that there are five different kinds of capitalism, according to the institutional complementarities in five domains: product markets, labour relations, financial systems, social protection and education. Consequently, capitalism takes one of the following five forms: liberal market capitalism (United States, UK, Canada, and Australia), Asian capitalism (Japan and Korea), continental European capitalism (Germany, France, Switzerland, Belgium, Ireland, Norway, and Austria), social-democrat capitalism (Denmark, Finland and Sweden) and Mediterranean capitalism (Spain, Greece, Italy, and Portugal). Amable (2005: chapter 3) characterizes these types of capitalism as follows.
In liberal market capitalism, the intensity of competition in the goods market makes firms particularly sensitive to unfavourable supply or demand shocks, to which they respond by changes in prices and, when this is not enough, in quantities. Easy changes in employment (due to labour market flexibility) and sophisticated financial markets allow firms to modify their strategies rapidly in the face of changing conditions. However, an underdeveloped social-protection system does not make specific investment safe in this environment, and competition extends to the education system, in which universities compete for the best students from a non-homogeneous secondary system.
Under social-democrat capitalism, strong foreign competition demands some labour market flexibility, but part of this flexibility is reached by means of a permanent formation of a highly qualified labour force. Workers´ specific investment is kept safe by moderate protection of employment, strong social protection and easy access to education and training, thanks to active employment policies. Coordinated wage negotiation and a centralized financial system favour innovation and long-term strategies.
Continental European capitalism also has high social protection and moderate employment protection, although the former is lower and the latter is higher than in social-democrat capitalism. Again, a centralized financial system encourages long-term industrial strategies. Labour force formation is achieved at a lower scale than in social-democrat capitalism. Hence there is somewhat less room for labour flexibility and fast restructuring of firms than in social-democrat capitalism. Productivity gains are obtained by lowering employment, which is possible because of social-protection benefits, such as pre-retirement agreements.
Mediterranean capitalism is based on more employment protection and less social protection than the continental European type. Employment protection is possible because of relatively weak competition in the goods market and because of the absence of short-term financial constraints due to a centralized financial system. A limited education level does not allow strategies based on high skills/salaries.
Asiatic capitalism is based upon collaboration among the large business groups, the state and a centralized financial system, which supports longterm strategies. Workers specific investments are protected by de facto employment protection, with possibilities of reorientation inside the group.
Developed countries in our sample were thus classified in this way. As Amable´s (2005) classification relates only to developed countries, it is insufficient for developing countries. However, taking colonialism into account, it may be assumed that the institutions of a former colony were moulded before independence. Hence developing countries were classified according to the European language that is most used in the country. Language is taken as a proxy for the European country that most influenced a country´s institutions, as several countries were colonies of European empires. In other cases, the decision was based upon the country´s shared permanence under the same empire, e.g. Turkey and Greece.
Still, developed and developing countries were separated, as there are several institutional differences. Finally, former socialist countries were grouped as transition economies. This leads to a classification of eleven groups (see table 3a 3b and appendix 2).
Note that, regardless of their degree of development, countries with market or European capitalism, as well as transition economies, do not tend to have demand cycles: they are either Goodwin or atypical. In contrast, developing countries with a Mediterranean capitalism do not tend to have Goodwin cycles: they are either demand or atypical. In other cases, such as Social Democrat, Asian, others, and developed Mediterranean capitalism (see appendix 2), there is no clear tendency.
CONCLUSIONS
Quantitative evidence does not strongly support Goodwin´s model, as the predicted centres lie outside the actual circles. This may be caused by the particular specification of the model, e.g. linear instead of non-linear real Phillips curve. Qualitative evidence is mixed. For the sample of 67 countries, 26 have evidence of cycles similar to those predicted by Goodwin, 9 have evidence of demand cycles and 32 were atypical. The diversity is not readily related to the degree of development, and it was suggested that explaining this would require a better understanding of the different forms of capitalism in which countries evolved around the world.
Goodwin cycles seem to be more a feature of countries with market or European capitalism, as well as of transition economies, while demand cycles tend to appear more in developing countries with a Mediterranean capitalism. Further studies should delve more into how the institutions typical of each kind of economy affect its dynamics. This would allow the building of more specific models that explain cycles in each kind of country. It is highly plausible that, once these factors are taken into account, Goodwin´s model will prove to be an important part of the explanation, at least for some of the countries.
Finally, it should be noted that looking for evidence in the case of a highly stylised model such as that of Goodwin should not be interpreted in the standard Popperian way. Not finding a cycle in a particular case is not necessarily a proof that the model does not hold. Rather, the objective of collecting the evidence is to provide stylised facts that can feed or be explained by further developments of a still abstract model. In this sense, looking at the actual data helps to suggest questions and avenues for future research and development.
APPENDIX 1. ECONOMETRIC ESTIMATION
For the econometric estimation we follow Harvie´s methodology for all variables of the model. In addition the state variables, i.e. u, v were passed trough the Hodrick - Prescott Filter in order to release the tendency. For the productivity growth, labor force growth and the Phillips curve estimation the parameters were estimate using ordinary least square (OLS) regressions. For countries with more than 17 data observations, we ran a unit root test and a cointegration test
Parameter estimation
Productivity growth α
An exponential productivity growth function a = a0 eαt is assumed, where α is the constant growth rate. The value of α is estimated for each country using Ordinary Least Squares (OLS) from the following equation

Labour force growth β
It was used a similar exponential function for the labour force growth n = n0 eβt, where β is the constant growth rate, and it was also estimated by OLS for the following equation:

Capital-output ratio σ
In the model, Goodwin assumes a constant capital-output ratio σ = k / q so a simple estimation of the mean for the variable was calculated for each country.
Phillips curve γ and ρ
We calculated a long run Phillips curve by the following equation
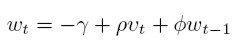
Equation for the estimated centers and period
The variables u and ν are the central points of the closed cycle; T is the period; α, the Productivity growth; β, the Labour force growth; σ, the Capital-output ratio; and γ, ρ are the Phillips curve parameters, where

APPENDIX 2. GRAPHICS BY TYPE OF CYCLE








REFERENCES
[1] Abraham, K. and Haltiwanger, J. (1995). Real wages and the business cycle. Journal of Economic Literature, 33(3), 1215-1265. [ Links ]
[2] Acemoglu, D., Johnson, S. and Robinson, J. A. (2001). The colonial origins of comparative development: an empirical investigation. American Economic Review, 91(5), 1369-1401. [ Links ]
[3] Amable, B. (2005). Le cinq capitalismes: diversité des systèmes économiques et sociaux dans la mondialisation. Paris: Editions du Seuil. [ Links ]
[4] Arrighi, G. (1978). La geometría dell´imperialismo. Milano: Giangiacomo Feltrinelli Editore. [ Links ]
[5] Atkinson, A.B. (1969). The timescale of economic models: how long is the long run? The Review of Economic Studies, 36(2), 137-152. [ Links ]
[6] Barbosa-Filho, Nelson H. and Taylor, L. (2006). Distributive and demand cycles in the US economy-a structuralistGoodwin model. Metroeconomica, 57(3), 389-411. [ Links ]
[7] Bhaduri, A. (1969). On the significance of recent controversies on capital theory: A Marxian view. Economic Journal, 79(315), 532-539. [ Links ]
[8] Bhaduri A. and Marglin S. (1990), Unemployment and the real wage : the economic bases for contesting political ideologies. Cambridge Journal of Economics, 14(4), 375-393. [ Links ]
[9] Canry, N. (2005) Wage-led regime, profit-led regime and cycles: a model. Economie Appliquée, 8(1), 143-163. [ Links ]
[10] Desai, M., Goodwin, R.M., Kruger, M. and Vercelli, A. (1984). Nonlinear Models of Fluctuations and Growth, an international symposium, Siena, Italy, 24-27, March 1983. Berlin, New York: Springer-Verlag. [ Links ]
[11] Desai, M., Henry, B., Mosley, A. and Pemberton, M. (2004). A Clarification of the Goodwin Model of The Growth Cycle. Journal of Economic Dynamics and Control, 30(12), 2661-2670. [ Links ]
[12] Dibeh, G., Luchinsky,D. G., Luchinskaya,D.D. and Smeliansky, V.N. (2007). A Bayesian estimation of a stochastic predator-prey model of economic fluctuations. In Kertész, J. Bornholdt, S. Mantegna, R.N. (eds) Noise and Stochastics in Complex Systems and Finance. Proceedings of SPIE, paper 6601-41. [ Links ]
[13] Duménil G. and Lévy D. (1999). Being Keynesian in the Short Term and Classical in the Long Term: The Traverse to Classical Long-Term Equilibrium. The Manchester School, 67(6), 684-716. [ Links ]
[14] Entov, R.M. and Poletayev, A.V. (1987). On the long-term dynamics of the rate of return. In Vasko, T (ed). The Long-Wave Debate (pp. 105-118). New York: Springer Verlag. [ Links ]
[15] Flaschel, P. and Groh, G. (1995). The classical growth cycle: reformulation, simulation and some facts. Economic Notes, 24, 293-326. [ Links ]
[16] Garegnani, P. (1970). Heterogeneous capital, the production function and the theory of distribution. Review of Economic Studies, 37(3), 407-436. [ Links ]
[17] Goodwin, R.M. (1967). A growth cycle. In Feinstein, C.H. (ed.) Socialism, Capitalism and Economic Growth (pp. 54-58). Cambridge: Cambridge University Press. [ Links ]
[18] Goodwin, R.M. (1972). A growth cycle. In Hunt, E.K. and Schwartz, J.G. (eds.) A Critique of Economic Theory (pp. 442-449). Harmondsworth: Penguin. [ Links ]
[19] Goodwin, R.M. (1984). Disaggregating models of fluctuating growth. In Goodwin, R.M., Krüger, M. and Vercelli, A. (eds.) Nonlinearmodels of fluctuating growth (pp. 67-72). Berlin: Springer. [ Links ]
[20] Goodwin, R.M. (1987). The economy as an evolutionary pulsator. In Vasko, T (ed.) The Long-Wave Debate (pp. 27-34). New York: Springer Verlag. [ Links ]
[21] Harcourt, G.C. (1972). Some Cambridge Controversies in the Theory of Capital. Cambridge: Cambridge University Press. [ Links ]
[22] Harvie, D. (2000). Testing Goodwin: growth cycles in ten OECD countries. Cambridge Journal of Economics, 24(3), 349-376. [ Links ]
[23] Kondratieff, N.D. and Stolper,W.F. (1935). The long waves in economic life. Review of Economic and Statistics, 17(6), 105-115. [ Links ]
[24] La Porta, R., Lopez de Silanes, F., Shleifer, A. and Vishny, R. (1999). Corporate ownership around the world. Journal of Political Economy, 54(2), 471-518. [ Links ]
[25] Moreno, A. M. (2002). El Modelo de Ciclo y Crecimiento de Richard Goodwin. Una evaluación empírica para Colombia. Cuadernos de Economía, 21(37), 1-20. [ Links ]
[26] Schumpeter, J.A. (1954). History of Economic Analysis. London, George Allen & Unwin. [ Links ]
[27] Solomou, S. (1987). Phases of Economic Growth, 1850-1973; Kondratieff Waves and Kuznets Swings. Cambridge: Cambridge University Press. [ Links ]
[28] Solow, R. (1990). Goodwin´s Growth Cycle: Reminiscence and Rumination, publicado. In Velupillai, K. (ed). Nonlinear Multisectoral Macrodynamics (pp. 31-41). London: McMillan. [ Links ]
[29] Sterman, J. D. (1987). The economic long wave: theory and evidence. In Vasko, T (ed). The Long-Wave Debate (pp. 127-161). London: Springer Verlag. [ Links ]
[30] Velupillai, K. V. (1998). Richard Goodwin (1919-1996). The Economic Journal, 108(450), 1436-1449. [ Links ]
[31] Veneziani, R. and Mohun, S. (2006). Structural stability and Goodwin´s growth cycle. Structural Change and Economic Dynamics, 17(4), 437-451. [ Links ]
[32] World Bank (2008). Global Purchasing Power Parities and Real Expenditures. 2005 International Comparison Program. Washington: International Bank of Reconstruction and Development / The World Bank. [ Links ]
[33] Zarnowitz, V. (1985). Recent work on business cycles in historical perspective: A review of theories and evidence. Journal of Economic Literature, 23(2), 523-580. [ Links ]













 [1]
[1]  [2]
[2]  [3]
[3]  [4]
[4] 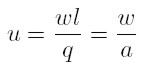 [5]
[5]  [6]
[6]  [7]
[7]  [8]
[8]  [9]
[9]  [10]
[10] 
