Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.29 no.53 Bogotá July/Dec. 2010
UNA REVISIÓN CRÍTICA DE LAS TÉCNICAS DE FILTRADO PARA LA TEORÍA DE LOS CICLOS ECONÓMICOS REALES
Fredy Alonso Vásquez Bedoya*
Sergio Iván Restrepo Ochoa**
John Fernando Lopera Sierra***
* Magister en Economía. Profesor e Investigador, Universidad de Antioquia (Medellín, Colombia). Dirección de correspondencia: Universidad de Antioquia, Departamento de Matemáticas y Estadística, Oficina 13-110, Apartado 1226 (Medellín, Colombia). E-mail: favasquez@econommicas.udea.edu.co.
**Ph.D. en Economía. Profesor Asociado e Investigador, Universidad de Antioquia (Medellín, Colombia). Dirección de correspondencia: Universidad de Antioquia, Departamento de Matemáticas y Estadística, Oficina 13-122, Apartado 1226 (Medellín,Colombia). E-mail: siro@economicas.udea.edu.co.
*** Magister en Economía. Investigador, Universidad de Antioquia (Medellín, Colombia).Dirección de correspondencia: Calle 42C N. 86A-35, Barrio la América (Medellín, Colombia). E-mail: jflopera@gmail.com.
Este artículo fue recibido el 25 de julio de 2008, la versión ajustada fue recibida el 30 de abril de 2010 y su publicación aprobada el 30 de junio de 2010.
Resumen
Este artículo presenta una revisión de diferentes investigaciones con respecto a dos elementos básicos de la teoría de los ciclos económicos reales: los factores que determinan los ciclos económicos y las técnicas de filtrado (estadísticas o económicas) que permiten estimarlos. El trabajo concluye, al igual que otros estudios, que cuando se utilizan diferentes técnicas de filtrado es posible encontrar distintos hechos estilizados, lo cual condiciona las interpretaciones sobre los factores que determinan los ciclos.
Palabras clave: ciclos económicos reales, técnicas de filtrado, series de tiempo. JEL: C22, C32, E13, E33.
Abstract
This article reviews different academic research concerning two basic elements of the theory of real business cycles: the determinants of economic cycles, and the filtering techniques (statistical or economic) that allow their estimation. The paper concludes, as many other studies, that when using different filtering techniques it is possible to find different stylized facts, which condition the interpretations of the factors that determine the cycles.
Key words: real business cycles, filtering techniques, time series. JEL: C22, C32, E13, E33.
Résumé
Cet article présente une révision de différentes recherches à l´égard de deux éléments de base de la théorie des cycles économiques réels : les facteurs qui déterminent les cycles économiques et les techniques de filtrage (statistiques ou économiques) qui permettent son estimation. Le travail conclut, à l´égal que d´autres études, que si on emploi de différentes techniques de filtrage il est possible de trouver des faits stylisés différents, ce qui conditionne les interprétations sur les facteurs qui déterminent les cycles.
Mots clés : cycles économiques réels, techniques de filtrage, séries temporelles. JEL : C22, C32, E13, E33.
A las fluctuaciones del producto alrededor de su tendencia en el tiempo y las variaciones asociadas de las distintas series económicas en torno a su respectiva tendencia, se les conocen como ciclos económicos. Este tema discutido inicialmente por Burns yMitchell (1946), ha dado lugar a muchas investigaciones teóricas y empíricas, que con relativo éxito explican este fenómeno. Los trabajos teóricos intentan principalmente definir tres cosas:
1. ¿Cuál es la mejor forma de explicar la evolución de los principales agregados macroeconómicos?
2. Determinar qué origina y a qué se debe la dinámica de los ciclos económicos, identificando si son de carácter nominal o real.
3. Establecer qué mecanismos de propagación hacen que se mantengan en el tiempo.
Dentro de este tipo de trabajos, hay algunos que se fundamentan enmodelos con choques monetarios, inflexibilidad de precios o tasas de interés, u otro tipo de fricciones (Lucas, 1972; Barro, 1976, 1980). Otros utilizan modelos con choques reales, a saber, cambios en la productividad suponiendo que la reacción óptima de la economía a tales choques es el mecanismo por el cual se propagan en el tiempo, (Kydland y Prescott, 1982; Long y Plosser, 1983; Hansen, 1985; King et al., 1988). A los últimos modelos se les denomina modelos de Ciclos de Económicos Reales (CER).
Por su parte, los análisis empíricos intentan aislar el componente de tendencia de una serie, y determinar un conjunto de propiedades y regularidades de los ciclos económicos. Sin embargo, no hay un consenso sobre las propiedades de la tendencia y su relación con el componente cíclico. Esto ha dado lugar a que se utilicen técnicas basadas en la teoría económica o en la estadística. Las primeras son necesarias porque antes de seleccionar las variables económicas y de reportar los hechos, se requiere una teoría que explique el mecanismo que origina las fluctuaciones económicas. En el segundo caso, las técnicas estadísticas, permiten establecer el tipo de tendencia que una serie presenta y la relación exacta entre los componentes de tendencia y cíclico (Canova 1998).
Entre las principales técnicas de tipo económico pueden mencionarse los modelos de tendencia determinista común y los modelos de tendencia estocástica común; mientras que, entre las principales técnicas estadísticas se puede mencionar: funciones polinomiales del tiempo, diferencias de primer orden, filtro de Hodrick y Prescott, técnica de Beveridge y Nelson, modelos de componentes no observables, métodos del dominio de la frencuencia, modelos de un índice dimensional, filtro de paso de banda, filtros de Butterworth, filtro de Kalman, y filtro de Gonzalo y Granger.
Este trabajo tiene como propósitos: presentar las principales técnicas de filtrado utilizadas en la macroeconomía dinámica y en la literatura de los ciclos económicos reales para aislar la tendencia de una serie de tiempo; y mostrar el estado del debate de las implicaciones que tiene para la explicación de los ciclos económicos el usar una u otra técnica de filtrado. Es importante aclarar que si bien se enuncian brevemente algunos de los principales elementos de los modelos de ciclos económico reales, no se pretende dar un aporte general a la teoría de los ciclos reales.
El documento está organizado en cuatro secciones. En la primera se define el ciclo económico y se presentan algunos trabajos que han contribuido a la comprensión de las fluctuaciones económicas desde el punto de vista de los modelos de CER. En el segundo apartado se describen las principales técnicas de filtrado usadas para aislar la tendencia de una serie económica. En la tercera parte, se presentan algunas investigaciones que han cuestionado los métodos de filtrado. El cuarto segmento está dedicado a las conclusiones.
LOS CICLOS ECONÓMICOS REALES (CER)
Las primeras investigaciones sobre ciclos económicos se desarrollaron en la primera mitad del siglo XX. El primer trabajo fue elaborado por Mitchell (1913), quien descompone una serie de tiempo económica en secuencias de ciclos, dividiendo cada ciclo en cuatro fases diferentes. Posteriormente, Burns y Mitchell (1946) presentan una definición de ciclo económico con dos características básicas: el comovimiento entre variables económicas individuales (el producto, el ingreso, los precios, la tasa de interés y las transacciones bancarias); y la división del ciclo económico en 4 fases: expansiones, recesiones, contracciones y recuperaciones, para lo cual estudian el comportamiento de la economía en cada una de ellas1.
Las investigaciones posteriores a Burns y Mitchell buscan identificar qué origina las fluctuaciones económicas valiéndose de modelos en los cuales choques de diferente índole pueden originar y explicar los ciclos económicos. Un enfoque empleado en la macroeconomía dinámica para evaluar los modelos de CER, consiste en identificar su capacidad para replicar las características cíclicas de las fluctuaciones económicas, validando para ello, los hechos estilizados de los ciclos económicos. Algunos trabajos recomiendan evaluar el componente cíclico de cada variable observada o generada por un modelo, enfatizando en su volatilidad –medida como la desviación estándar–, y en los comovimientos entre el componente cíclico de cada variable con el componente cíclico del producto –medidos a través de el coeficiente de correlación y clasificados según su magnitud y signo en procíclicos, contracíclicos y acíclicos.
Un trabajo pionero de modelos de CER con choques tecnológicos como origen de las fluctuaciones económicas es el de Kydland y Prescott (1982)2. Los autores sugieren que los ciclos económicos pueden ser estudiados empleando modelos de equilibrio general y que es posible unificar la teoría del crecimiento y de los ciclos económicos, a su vez, enfatizan en que los modelos de ciclos económicos deben ser consistentes con las regularidades empíricas del crecimiento económico en el largo plazo. Además, al emplear metodologías de calibración muestran que es posible ir más allá de la comparación cualitativa de las propiedades estadísticas del modelo con los hechos estilizados.
Kydland y Prescott (1982) utilizan un modelo en el cual se consideran los siguientes supuestos:
1. Se requiere de más de un periodo para construir capital productivo.
2. Sólo los bienes finales son parte del stock de capital productivo.
3. Una función de utilidad no separable en el tiempo para admitir mayor sustitución intertemporal por el ocio.
4. Hay una familia representativa que vive infinitamente.
5. El consumidor valora tanto el consumo como el ocio.
6. Las fluctuaciones en el empleo son centrales para explicar los ciclos económicos.
Los componentes estocásticos exógenos en el modelo son los choques en la tecnología y los parámetros son calibrados usando supuestos del estado estacionario. El modelo considera una regla de acumulación de capital que incluye nuevos proyectos de inversión y el stock de inventarios de inversión. La función de producción del tipo CES utiliza capital, trabajo e inventarios como insumos en la producción. En la tecnología se identifica un choque permanente y otro transitorio que difieren en su persistencia.
Kydland y Prescott (1982) juzgan su modelo por la capacidad que posee para replicar las principales características estadísticas de los ciclos económicos de Estados Unidos. Para ellos, los datos generados por el modelo presentan patrones de volatilidad, persistencia y comovimientos similares a los que poseen los datos trimestrales de Estados Unidos en el periodo 1950:1-1979:2, hallazgo que en palabras de Rebelo (2005) es sorprendente puesto que el modelo no contempla la política monetaria que, según Friedman (1968), es un aspecto central de las fluctuaciones económicas. Además, se identifica que el consumo, la inversión y el trabajo son procíclicos, que el consumo es menos volátil que el producto, la inversión es más volátil que el producto y el trabajo es ligeramente menos volátil que el producto. A los modelos posteriores al de Kydland y Prescott (1982) se les denominó modelos de ciclos económicos reales, por su énfasis en el rol de los choques reales como conductores de las fluctuaciones económicas –particularmente choques tecnológicos.
Long y Plosser (1983) definen los ciclos económicos como el comportamiento de un conjunto de variables económicas tales como el producto, el empleo, el consumo, los precios y la inversión, haciendo énfasis en que los comovimientos de los diferentes sectores de la economía juegan un rol central en la generación de los ciclos económicos. Es así como utilizan un enfoque multisectorial para la producción, que propaga los efectos de las perturbaciones sobre el producto en el tiempo y entre sectores. En el modelo de Long y Plosser (1983) hay tres supuestos básicos:
1. Las preferencias son constantes en el tiempo y no están afectadas por choques exógenos aleatorios.
2. Todos los bienes de consumo, dados los precios, son demandados en cantidades positivas y son bienes normales, lo cual implica que los consumidores desean distribuir algún incremento no esperado en la riqueza en el tiempo y en bienes.
3. La tecnología de producción es factible y eficiente, tiene retornos constantes a escala, sustitución suave entre insumos, y la productividad marginal es estrictamente decreciente para un insumo dado.
Asimismo, hay un agente representativo que vive infinitamente con una dotación inicial de recursos, con posibilidades de producción y preferencias establecidas, que selecciona el plan de consumo y producción preferido de acuerdo con los precios de equilibro de la economía. Todas las actividades de la economía son descritas como repeticiones de ciclos de un periodo, en el cual choques aleatorios exógenos afectan la producción. La economía produce todos los bienes, cualquier bien es usado como insumo en la producción de otro o para el consumo, y la tasa de depreciación es del 100%. En cada periodo el agente representativo tiene dos restricciones, el tiempo dedicado al trabajo y al ocio deben ser igual a la dotación; y el uso total de los productos debe ser igual al producto total de la economía. Dado el estado inicial de la economía, la evolución intertemporal de las cantidades y precios de equilibrio se pueden definir como un proceso estocástico multivariado.
De acuerdo con la solución de equilibrio, el producto destinado al consumo es una función creciente del producto total y la cantidad de un producto destinado a la producción de otro es una función creciente de la cantidad total disponible del producto. Además, un producto al tener múltiples usos y estar sometido a choques inesperados, puede comprometer su realización futura y originar choques en otros sectores de la economía. Lo anterior, no es más que la explicación de los comovimientos y la persistencia de las series temporales. Finalmente, para Long y Plosser (1983) hay consistencia entre algunas de las regularidades empíricas de los ciclos económicos y las halladas en la economía simulada, explícitamente la relación existente entre las covarianzas de series del producto correspondientes a distintos sectores de la economía.
Por su parte, Hansen (1985) presenta un modelo de crecimiento estocástico unisectorial, en el que los ciclos económicos se deben a choques en la tecnología y el trabajo es indivisible, por tanto, las fluctuaciones en el total de horas trabajadas se deben a las variaciones en el número de trabajadores empleados y no en las horas por trabajador empleado3. El autor calibra el modelo con base en datos de Estados Unidos para el periodo 1955:3-1984:1 y, concluye que, la economía con indivisibilidad del factor trabajo presenta fluctuaciones más notorias que una que considera su divisibilidad, y las fluctuaciones en la mayoría de las variables de la economía son superiores a las encontradas en la economía hipotética, en particular, el consumo fluctúa mucho más en la economía observada que en la simulada.
King et al. (1988) consideran choques tecnológicos como origen de los ciclos económicos. Para ello utilizan un modelo neoclásico unisectorial con acumulación de capital y el trabajo como variable de elección. De acuerdo con los autores la discusión gira en torno a las siguientes cuestiones: ¿qué rol juegan los modelos de crecimiento económico en el estudio de las fluctuaciones económicas? ¿Cómo extraer el componente cíclico de las series temporales generadas por el modelo? ¿Cuál es la dinámica del modelo al introducir choques en la tecnología? ¿Replicará el modelo, en presencia de choques tecnológicos, los hechos estilizados de las series de tiempo económicas?
En el modelo de King et al. (1988) hay un gran número de individuos idénticos que viven infinitamente y derivan su utilidad del consumo de un único bien y del ocio. La función de utilidad, es creciente en el consumo y el ocio; la tecnología de producción, con el capital y el trabajo como insumos, tiene rendimientos constantes a escala; hay una perturbación tecnológica temporal que afecta la productividad total de los factores y; los choques tecnológicos permanentes sólo afectan a la productividad marginal del trabajo. En este modelo el bien final puede ser destinado al consumo o la inversión. En cada periodo el agente representativo tiene dos restricciones: el tiempo dedicado al trabajo y al ocio no debe exceder la dotación total de tiempo y; el uso del producto no debe exceder la dotación total de la economía.
Con el fin de garantizar la existencia de una senda de crecimiento de equilibrio en la cual las variables per cápita crezcan a la misma tasa y las fracciones de tiempo dedicadas a cada actividad permanecen constantes, King et al. (1988) utilizan funciones de utilidad logarítmicas. Los parámetros del modelo son calibrados utilizando supuestos del estado estacionario de la economía hipotética, con base en datos de la economía de Estados Unidos para el periodo 1948:1-1986:4. King et al. (1988) utilizan parametrizaciones alternativas del modelo neoclásico básico que resultan de alterar algunos supuestos sobre las preferencias y la tecnología, por ejemplo, la tasa de depreciación del capital es menor al 100%, y hay cambios en la elasticidad de la oferta laboral.
De acuerdo con los autores, cuando hay choques temporales en la productividad, el modelo neoclásico puede sustituir intertemporalmente los bienes y el ocio, pero no produce una correlación positiva entre el producto y el empleo similar a la que exhiben los datos reales; pero, con choques tecnológicos persistentes, el modelo captura algunos hechos estilizados de los ciclos económicos de Estados Unidos.
El modelo identifica un comportamiento procíclico del empleo, el consumo y la inversión, y simula una volatilidad similar a la observada para el producto, el consumo y la inversión. Sin embargo, existen algunos aspectos que no son capturados debidamente por el modelo, el consumo, la inversión y el trabajo están más correlacionados con el producto en el modelo que en los datos observados. Cuando la tasa de depreciación del capital es menor al 100%, el modelo no presenta el mismo nivel de persistencia que se encuentra en los datos de la economía observada.
Para King et al. (1988), su modelo difiere de los propuestos por Hansen (1985) y Prescott (1986) ya que no filtra las series de datos observados y generados por el modelo para remover los componentes de baja frecuencia. En Hansen (1985) y Prescott (1986), las series filtradas del trabajo y producto tienen volatilidades similares tanto en el modelo como en los datos observados; pero en King et al. (1988), la volatilidad del trabajo es la mitad de la del producto.
Posteriormente, King y Rebelo (2000) presentan algunos desarrollos de los modelos de CER en la década del noventa, tanto en su estructura como en bondades y falencias. Así, el modelo básico de CER requiere de grandes choques tecnológicos como fuente principal de las fluctuaciones económicas. En algunos estudios sobre productividad con variación en los factores no observados, dichos choques tienen un efecto mucho más pequeño, sugiriendo una inminente desaparición de los ciclos económicos.
Adicionalmente, King y Rebelo (2000) mencionan la posibilidad de utilizar choques distintos a los tecnológicos, como los fiscales y monetarios, para explicar los ciclos económicos. Sin embargo, advierten que los choques fiscales, no producen por sí mismos, patrones reales de comovimientos entre las variables económicas y; en el caso de los choques introducidos vía política monetaria, los efectos son pequeños. Por otro lado, afirman que el modelo de crecimiento neoclásico permite obtener series de tiempo con patrones de crecimiento, persistencia, comovimientos y volatilidad similares a las de las economías reales.
Rebelo (2005), presenta algunas de las principales contribuciones de los modelos de CER a la comprensión de las fluctuaciones económicas, para ello expone los tipos de choques que se utilizan, tales como: tecnológicos, monetarios y fiscales; y en el precio del petróleo. Además, da cuenta del debate existente sobre el papel de los choques tecnológicos en la explicación de las fluctuaciones económicas y las implicaciones que han tenido en investigaciones macroeconómicas.
Como conclusión, los modelos de ciclos económicos reales, haciendo uso del modelo neoclásico de crecimiento, permiten pensar en la posibilidad de que las fluctuaciones económicas sean una manifestación de procesos de crecimiento estocástico –vía choques tecnológicos.
Un interrogante presente en la literatura de los CER y considerado por King et al. (1988), es el cómo aislar el componente cíclico de las series producidas por un modelo. A esto la literatura ha dado respuesta parcialmente al presentar un conjunto de técnicas para aislar el ciclo económico, pero sin encontrar un consenso sobre cuál es el método más apropiado.
DESCOMPOSICIÓN DE SERIES TEMPORALESY TÉCNICAS DE FILTRADO
Las investigaciones de los modelos de CER al retomar a Burns y Mitchell (1946), indagan sobre cómo se deben separar los elementos del ciclo económico de la evolución suave (tendencia) y de la variación rápida (componente irregular) de la serie temporal. Por ejemplo, en el caso de la hipótesis de los componentes subyacentes, una serie temporal, yt puede descomponerse en todos o algunos de los siguientes elementos: tendencia xt, ciclo ct estacionalidad γt e irregularidad εt siendo el punto de partida de un número importante de métodos para extraer cada uno de los componentes de una serie temporal4.
El componente de tendencia representa la evolución de largo plazo de una serie económica y cambia suavemente en el tiempo, con perturbaciones cuya duración es mayor a 32 trimestres. Por el contrario, las fluctuaciones cíclicas cambian rápidamente en el tiempo y son movimientos alrededor de la tendencia, que reflejan oscilaciones de duración entre 8 y 32 trimestres. El componente estacional de la serie representa movimientos periódicos de duración menor o igual a un año; mientras que el componente irregular representa movimientos esporádicos sin referente alguno, e incluye todo aquello que los demás componentes no contemplan.
Se consideran como determinantes de la tendencia la acumulación de capital, el crecimiento de la población, el cambio tecnológico, el aprendizaje por la experiencia, y la composición y cualificación del capital humano. Hay que tener en cuenta que muchos de los factores que afectan la tendencia son la causa del comportamiento cíclico, por lo que no conviene ni es posible imponer una distinción clara. Por su parte, los determinantes del componente cíclico se asocian a las consecuencias que tiene la política económica sobre la economía en su conjunto, pero sus efectos son transitorios sobre la serie. El componente estacional se vincula principalmente a factores institucionales, climáticos y técnicos que evolucionan de forma suave desde una perspectiva de largo plazo5.
Cabe señalar que en el análisis empírico existe controversia sobre lo que es el componente de tendencia de una serie económica. No hay consenso sobre lo que constituye las fluctuaciones cíclicas y tampoco en si se deben usar técnicas estadísticas o económicas para aislar la tendencia del componente cíclico (Canova, 1998).
A continuación, utilizando y tomando elementos de Canova (1998), se exponen brevemente las técnicas (económicas y estadísticas) que se utilizan para extraer el ciclo de una serie de tiempo económica. En los desarrollos presentados en el resto del trabajo se denota el logaritmo natural de la serie por yt, su tendencia por xt y su componente cíclica por ct.
Técnicas económicas
Según Moral (2000) el enfoque económico estudia la "habilidad" de un conjunto de supuestos teóricos, plasmados en relaciones y modelos matemáticos, que pretenden replicar las fluctuaciones cíclicas y comovimientos observados.
Modelos de tendencia determinista común
El método de tendencia determinista común se atribuye a King et al. (1988) y considera que las variables endógenas tienen una tendencia determinista común y las fluctuaciones alrededor de la tendencia son de naturaleza transitoria (Canova, 1998). Entonces, la ecuación general de yt viene dada por:
Siendo δ la tasa de crecimiento del progreso tecnológico y t una variable de tendencia; es decir, el componente de tendencia es una función lineal del tiempo6. Por tanto, los parámetros de la regresión se pueden estimar por mínimos cuadrados lineales. Y los movimientos seculares de la serie son:
El componente cíclico de la serie no es más que los residuales de la regresión anterior, es decir:
Aunque el modelo de tendencia lineal es una aproximación útil para estimar el componente secular, el supuesto simplificador de crecimiento constante en el tiempo hace que su uso sea escaso. En consecuencia, en la literatura se propone admitir la existencia de una tendencia no lineal, utilizando para ello aproximaciones polinomiales del tiempo.
Nelson y Plosser (1982) proponen representar el componente secular utilizando un proceso estocástico que no retorna a una tendencia determinista, por lo que las innovaciones afectan el valor futuro de la serie. Una aplicación de estos modelos se presenta en Trajtenberg (2004).
Modelos de tendencia estocástica común
En este caso las propiedades de largo plazo de las variables endógenas se deben a choques tecnológicos no estacionarios. Al considerar la hipótesis de una tendencia común estocástica en la productividad, se puede contrastar su presencia, medir su importancia y extraer estimadores de los valores realizados (King et al., 1991).
Para Stock y Watson (1988) la variable de tendencia (no estacionaria) y la variable cíclica (estacionaria) como lo menciona Canova (1998) se pueden expresar de la forma:
Donde A es un vector nxk, τt = μ + τt−1 + ηt es el factor de productividad marginal; ηt es ruido blanco serialmente incorrelacionado y representa las innovaciones, esto es, las desviaciones del crecimiento actual de su promedio; μ es la tasa de crecimiento promedio de la productividad; y C(1) y D(L) representan polinomios en el operador rezagos. Además,  .
.
Finalmente, el componente cíclico de la serie puede obtenerse como:
Técnicas estadísticas
Como la teoría económica no indica el tipo de tendencia que la serie manifiesta ni la relación exacta con el componente cíclico, es posible usar distintos supuestos y contrastes estadísticos para observarlas y determinarlas; es decir, sin un conjunto de hechos estadísticos las propiedades del componente secular de una serie de tiempo se vienen abajo (Canova, 1998, 477). Las técnicas estadísticas son enfoques empiristas o descriptivos de una serie, a partir de las cuales se estudian principalmente las características cíclicas: número de ciclos, duración total, duración de las fases de aceleración, correlaciones entre variables y relaciones de adelanto-retraso (Moral, 2000).
Funciones polinomiales del tiempo
En este método el componente de tendencia sigue un proceso determinista que se expresa mediante funciones polinómicas del tiempo, xt = f(t) y tanto la tendencia como el ciclo están incorrelacionados. La dificultad reside en la elección de la forma funcional, para ello la intuición dice que los movimientos seculares deberían ser una función suave del tiempo, luego la función para la tendencia debe ser continua en el tiempo y su primera derivada estar definida en todo su dominio (Trajtenberg, 2004). De acuerdo, con Canova (1998) una función polinomial para el componente de tendencia está dada por:

Siendo q típicamente pequeña,  un punto conocido en el tiempo, y t0 y t1 puntos en el tiempo para escalar el origen de la tendencia. Luego, el componente cíclico se estima restando de la serie el resultado de la estimación del componente secular. Una aplicación de esta técnica se presenta en Trajtenberg (2004).
un punto conocido en el tiempo, y t0 y t1 puntos en el tiempo para escalar el origen de la tendencia. Luego, el componente cíclico se estima restando de la serie el resultado de la estimación del componente secular. Una aplicación de esta técnica se presenta en Trajtenberg (2004).
Diferencias de primer orden
En esta técnica el componente de tendencia es una función de sus valores pasados. Los valores más cercanos de la serie tienen un mayor peso en la determinación de la variable y cada valor se pondera de modo que la suma de los coeficientes sea igual a uno. Por tanto, este componente sigue un paseo aleatorio sin deriva, el componente cíclico es estacionario y ambos están incorrelacionados, esto es, E[xt ct] = 0. Se asume que la serie tiene raíz unitaria, la cual se debe al componente de tendencia, es decir:

Siendo εt un término de perturbación y εt ∼ N (0, σ2); = yt−1. El estimador para el componente cíclico se obtiene a partir de:

Filtro de Hodrick y Prescott
Esta técnica desarrollada por Hodrick y Prescott (1997, filtro de HP en adelante), es una solución del problema de minimización de la variabilidad del componente cíclico de la serie observada sujeto a una condición de suavidad del componente de tendencia. Este método extrae una tendencia estocástica que se mueve sin problemas en el tiempo y es incorrelacionada con el componente cíclico. De acuerdo con Hodrick y Prescott (1980), una serie de tiempo económica se puede descomponer en tendencia y ciclo:

Y el componente de tendencia se obtiene de resolver el siguiente problema:

Siendo T el tamaño de la muestra y λ un parámetro que penaliza la variabilidad de la tendencia, en otras palabras representa la suavidad. Cuanto mayor sea el valor del parámetro λ mayor es la suavización de la serie. En efecto, a medida que dicho parámetro se aproxima a cero la tendencia coincide con la serie original. Cuando λ→∞ la tendencia se aproxima a una forma lineal xt = x0 + δt, δ > 0. El valor óptimo de λ es λ = σ 2 x / σ 2 c donde σx y σc son las desviaciones de las innovaciones en la tendencia y en el ciclo, respectivamente.
Después de tomar las condiciones de primer orden, realizar algunas manipulaciones algebraicas y hacer uso del operador de rezagos, el componente de tendencia de una serie económica se obtiene de la siguiente forma:

Siendo L el operador de rezago.
Por tanto, el componente de tendencia de una serie de tiempo económica, utilizando el filtro de HP se obtiene aplicándole a la serie de tiempo el polinomio de rezagos, [ 1 + λ(1 − L)2 (1 − L−1)2 ].
Para Avella y Ferguson (2003), una crítica común a este filtro es la elección del parámetro λ que es relativamente arbitraria. En la mayoría de los trabajos empíricos suele utilizarse los valores que Hodrick y Prescott (1980) proponen: 100, 1.600 y 14.400 para datos anuales, trimestrales y mensuales, respectivamente. El valor λ = 1.600 fue propuesto para datos macroeconómicos trimestrales de los Estados unidos correspondientes al periodo 1950-1979, sin embargo, se ha empleado en trabajos realizados para otras economías y otros periodos muestrales, lo cual ha suscitado discusiones sobre su elección.
Guerrero (2008) reseña algunos trabajos que han cuestionado el uso del filtro HP: Harvey y Jaeger (1993), Cogley y Nason (1995) y Park (1996). También resalta las propiedades estadísticas del filtro y sugiere escoger de manera objetiva el parámetro de suavización λ utilizado en el filtro, con el fin de estimar apropiadamente la tendencia de una serie. Por otro lado, cuestiona algunos métodos estadísticos sugeridos en la literatura para estimar el parámetro de suavización de la tendencia de series de tiempo económicas, dada su complejidad computacional y falta de interpretación del valor numérico de λ como son los presentados en Lee (2003), y Kohn et al. (1992). Basado en un modelo estadístico, propone un método para estimar la constante de suavización λ empleada por el filtro HP, teniendo en cuenta el tamaño de la muestra y fijando un porcentaje deseado de suavización para la tendencia. El autor afirma que el método sugerido es fácil de implementar y recomienda realizar estudios para elegir el porcentaje adecuado de suavización para los diferentes tamaños muestrales y grupos de series de tiempo, antes de ser usado en forma masiva.
En economía el filtro de HP se ha convertido en una herramienta estándar que permite estimar el componente cíclico de las series temporales y analizar así el comportamiento de las fluctuaciones económicas. Paralelamente, permite estimar el producto potencial, el cual es precisamente la tendencia de la serie temporal económica. Algunas aplicaciones del filtro se presentan en Gómez y Bengoechea (2000) y Restrepo y Vásquez (2004).
Técnica de Beveridge y Nelson
Para Beveridge y Nelson (1981) una serie de tiempo se puede expresar como un proceso estocástico que no retorna a una senda determinista, luego las innovaciones del producto afectan su valor futuro. Si el proceso estocástico no retorna a una senda determinista, una parte importante de las fluctuaciones cíclicas de la serie observada pueden deberse a la variación estocástica de la tendencia, que no queda eliminada (Nelson y Plosser, 1982).
Sea wt = (1−L) yt un proceso ARIMA estacionario con una representación de medias móviles wt = μ + γ (L) εt, donde εt ∼ i.i.d.(0, σ2 ) y γ(L) = φ(L)−1 θ(L) es un polinomio en el operador de rezagos con la raíz de φ(z) = 0 por fuera del círculo unidad.
Beveridge y Nelson (1981), mostraron que el componente secular de una serie se define como:

En otras palabras, el componente de tendencia es el pronóstico de largo plazo de la serie ajustado por la tasa de cambio de su media, kμ.
Se establece además que

En el caso del componente cíclico estos autores proponen la siguiente forma para determinarlo:

Según Morley (2010), hay dos maneras de interpretar los resultados de la descomposición de Beveridge y Neslon (1981). El pronóstico de largo plazo para la tendencia es un estimador de un componente permanente no observado o este pronóstico define un componente observado. Una aplicación de esta descomposición se presenta en Issler et al. (2008).
Modelo de componentes no observables
Harvey y Jaeger (1993) introducen al modelo yt = xt + εt un componente cíclico7:

Donde εt ∼ N(0, σ2), ∀t y E[ εt, εt-1] = 0. El componente de tendencia tiene la forma lineal:


Siendo βt la pendiente.
La tendencia, según Harvey y Jaeger (1993), es un proceso ARIMA(0, 2, 1); pero, si σ2 ς = 0 el proceso se reduce a un paseo aleatorio con deriva. Si σ2 η = 0 se obtiene un proceso determinista, xt = x0 + βt Finalmente, el componente cíclico es generado por un proceso estocástico de la forma:

Siendo ρ la amplitud del ciclo económico tal que 0 ≤ ρ ≤ 1 y λc la frecuencia del ciclo en radianes. Harvey y Jaeger (1993) sugieren un valor ρ = 2 con el fin de permitir que los procesos para el ciclo económico sean periódicos y exista un pico en su función de densidad espectral.
Por su parte, Clark (1987) sugiere un modelo de componentes no observados para una serie económica con el fin de distinguir entre una "tendencia suave" y una "tendencia irregular", dado por:

En este caso el componente de tendencia viene dado por la siguiente expresión:

El componente cíclico sigue un proceso ARMA estacionario e invertible, dado por: φ(L)ct = θq(L)εt.
Así mismo, las innovaciones para la tendencia y el ciclo se supone que están incorrelacionadas: cov(ηt , εt) = 0.
Una ventaja de la aproximación de componentes no observados es la estimación simultánea de la tendencia y el ciclo. En este caso, las series no estacionarias como el producto pueden ser modeladas sin necesidad de realizar transformaciones como la diferenciación (Scott, 2000, 6). Una aplicación de esta técnica se presenta en el trabajo de Domenéch y Gómez (2005).
Métodos del dominio de la frecuencia
En el análisis económico se trabaja con magnitudes que han sido observadas en el tiempo con una periodicidad determinada; pero es posible analizar dicha serie referenciada a la frecuencia y no al tiempo. Si una serie de tiempo presenta un comportamiento cíclico, es posible realizar una aproximación de la misma mediante funciones trigonométricas; por tanto, el estudio de las series temporales se realiza con respecto a la frecuencia de medición de los datos.
A las series trigonométricas que aproximan una función periódica se les denomina series de Fourier. Una función periódica tiene la siguiente característica:

Siendo T el periodo o intervalo de tiempo que transcurre entre repetición de los valores. En el caso de las funciones seno y coseno, T = 2π. Cualquier función periódica puede expresarse en términos de funciones trigonométricas sustituyendo a t en Y (t) por t = T(ω/2T), y si ω aumenta en 2π la función es igual a T. Es decir, la cantidad de tiempo que le toma a la función completar un ciclo es igual a (2π/ω). A ω se le conoce como la frecuencia de la función y se mide en radianes.
En esta metodología los componentes secular y cíclico de la serie económica son independientes. El secular tiene la mayor parte de su poder en una frecuencia baja del espectro y cuando se aleja de cero su poder se degrada rápidamente; además, el supuesto de identificación no lo restringe a ser determinista o estocástico, y permite cambios en la tendencia en el tiempo, siempre y cuando los cambios no sean demasiado frecuentes.
De acuerdo con los métodos de filtrado en el dominio de la frecuencia, el componente de tendencia de una serie de tiempo económica puede expresarse como:

Y la relación entre la densidad espectral de la serie de tiempo económica (yt) y el componente de tendencia (xt) corresponde a: a(ω)Fy(ω) = Fx(ω).
Siendo a(ω) la función de transferencia, definida como la transformada de Fourier de los coeficientes b(t) del filtro:

En este caso i representa la unidad imaginaria. Si los filtros son simétricos (bt = b−t ) la anterior ecuación se escribe como:

Así mismo, Fy(ω) y Fx(ω) son las transformaciones de Fourier de yt y xt, respectivamente. En el dominio del polinomio a(L) la transformada inversa de Fourier de a(ω) tiene la forma:

Siendo ω1 y ω2 los límites superior e inferior de la frecuencia. Entonces, un estimador válido del componente cíclico es (1 − a(L))yt.
Canova (1998), afirma que esta técnica permite una variabilidad no deseable de alta frecuencia, que no necesariamente se identifica con el ciclo económico.
Modelos de un índice dimensional
Para Stock y Watson (1989) los modelos de un índice dimensional suponen que si una serie tiene tendencia determinista o estocástica, o ambas, alguna combinación lineal de ellas no tiene tendencia. Así, el supuesto clave es que en el espectro de las series con baja frecuencia existe un proceso unidimensional común a todas las series. Entonces, la serie económica se puede expresar de la forma:

Siendo zt un proceso estocástico con 0 < Sz(ω) < M, ∀ω ∈ (ˆω, π); Sz(ω) la densidad espectral de zt; M un número pequeño, A un vector nx1 de ponderaciones y xt un vector independiente de ct.
Quah y Sargent (1992) proponen un índice de estructura dinámica para campos aleatorios, de la forma:

En este caso, Xj(t) j = 1, . . . ,N, t = 1, . . . , T es un segmento observado de un campo aleatoiro, U es un vector ortogonal kx1 de paseos aleatorios; B es un vector estacionario con media cero, y con todas sus entradas incorrelacionadas en j; y finalmente, aj es un vector 1xk de las distribuciones de rezago.
Filtro paso de banda
Esta técnica fue desarrollada por Baxter y King (1999), aísla las fluctuaciones económicas que persisten entre dos y ocho años, extrae la señal de tendencia de los datos y entrega series de tiempo que son estacionarias de orden menor o igual a dos, o que contienen tendencias deterministas en el tiempo.
Baxter y King (1999) diseñaron tres tipos de filtros de paso de banda: baja, media y alta frecuencia en el dominio del tiempo. El filtro de baja retiene los componentes que se mueven de forma lenta en los datos, mientras el de alta acepta sólo componentes que tienen una frecuencia menor o igual a una periodicidad p. La representación general del filtro es:

Siendo L el operador de rezagos y bh los ponderadores de promedios móviles infinitos. Estos últimos, se determinan hallando la transformada inversa de Fourier para la función de respuesta de la frecuencia, en la forma:

Donde β(ω) es la ponderación ideal para el filtro infinito. En el caso del filtro de orden finito la aproximación ideal es:

De forma similar al caso anterior, los ah son las ponderaciones muestrales para este filtro y la transformada de Fourier para los ponderadores es:

Esta función indica el grado de respuesta de y*t a yt en la frecuencia ω. Por tanto, para que un filtro tenga la propiedad de la reducción del componente de largo plazo, se requiere que la respuesta en la frecuencia sea cero, y estose consigue si:

Para Baxter y King (1999), cuando se elige la aproximación general ακ(ω) para el filtro específico β(ω) se debe considerar una estrategia que minimice la discrepancia en los ponderadores en la forma:

Siendo δ(ω) ≡ β(ω) − ακ(ω) la discrepancia que surge para la aproximación de la frecuencia ω y el número de rezagos seleccionado. No obstante, para Baxter y King (1999) no existe el número ideal de rezagos y su selección depende de la cantidad de datos disponibles. Una aplicación del filtro de Baxter y King se presenta en Gómez y Bengoechea (2000).
Filtros de Butterworth
Los filtros de Butterworth tienen su origen en los desarrollos de la ingeniería eléctrica y las telecomunicaciones, disciplinas en las cuales la necesidad de procesar señales es una actividad fundamental (Bógalo y Quiles, 2003). Estos filtros permiten la estimación de tendencias a largo plazo y la extracción directa de una señal cíclica mediante filtros de paso bajo y de paso de banda, respectivamente.
Filtros de paso bajo
Estos filtros son operadores ARMA cuya función de ganancia viene dada por:

En este caso, ω es la frecuencia expresada en radianes, ωc es la frecuencia de corte y, d es el grado del filtro. La expresión para el filtro es:

Siendo B el operador de rezagos, F = B−1, λ un parámetro asociado a la frecuencia del corte. El grado del filtro, está dado por: λ = [tan2d(ωc / 2)]−1.
Filtros de paso de banda
Para obtener un filtro de paso de banda en el dominio del tiempo, se aplica la siguiente transformación al filtro de paso bajo:

Por tanto, el filtro de paso de banda para obtener el componente cíclico de una serie es:
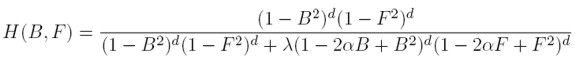
Siendo λ = [tan2d(ωc / 2)]−1.
Formalmente, el componente cíclico de una serie de tiempo se puede obtener como: ct = H(B,F)yt.
O de manera indirecta como: ct = yt − xt.
Siendo xt = L(B,F)yt.
Filtro de Kalman
El filtro de Kalman (1960) es un sistema de ecuaciones que entrega una solución del método de mínimos cuadrados y permite calcular un estimador lineal, insesgado y óptimo del estado de un proceso en cada momento del tiempo con base en la información disponible hasta t − 1, y actualizar las estimaciones con la información en el momento t (Solera, 2003, 4). La solución es óptima porque el filtro combina toda la información observada y el conocimiento previo acerca del comportamiento del sistema para producir una estimación de tal manera que el error sea mínimo; además, el filtro re-calcula la solución cada vez que una nueva observación es incorporada.
Este filtro estima el estado de  de un proceso en tiempo discreto, definido por una ecuación de la forma: Xt+1 = AXt + wt.
de un proceso en tiempo discreto, definido por una ecuación de la forma: Xt+1 = AXt + wt.
Con una medida Z ∈  dada por: Zt = MXt + vt.
dada por: Zt = MXt + vt.
Siendo las variables aleatorias wt, vt el error del proceso y de la medida, respectivamente. Se asume que son ruido blanco e independientemente distribuidas y lo hacen de la forma: wt ∼ N(0,Q), vt ∼ N(0,R).
La matriz A relaciona el estado en el periodo t − 1 con el periodo t. La matriz M relaciona el estado con la medición Zt.
En economía existen numerosas aplicaciones del filtro de Kalman, una de ellas se encuentra en el trabajo de Ruiz (2002), en el cual se presenta una generalización del filtro que es empleada en la calibración de parámetros de modelos estocásticos de crecimiento, bajo el supuesto de expectativas racionales.
Filtro de Gonzalo y Granger
Gonzalo y Granger (1995) proponen un procedimiento para estimar factores o tendencias comunes para un grupo de series que tienen el mismo orden de integración. La estimación de los factores comunes o tendencias comunes se logra encontrando combinaciones lineales de éstas que tengan un grado de integración menor que el de las series originales y cuando los términos de corrección de errores no causen en ellos bajas frecuencias.
Sea Yt un vector formado por p series de tiempo de integradas de orden 1 –I(1)– que se puede expresar de la forma: Yt = A1ft + A2Zt.
Siendo ft un vector formado por k series (con k < p), de tendencias comunes y Zt un vector de r series que representa la componente transitoria común y que es I(0).
Para llevar a cabo la descomposición de Gonzalo y Granger se procede de la siguiente manera. Primero se emplea el procedimiento de de Johansen8 (1988) para hallar las relaciones de cointegración entre las p series originales. Estas relaciones de cointegración determinan el componente transitorio común Zt. Luego se encuentra el componente de tendencia ft, que describe el comportamiento de largo plazo de las series y para ello se utiliza un procedimiento similar al de Johansen. Finalmente, se determinan las matrices de coeficientes A1 y A2 de tal manera que yt = A
El filtro de Gonzalo y Granger es un filtro razonable para analizar las característicasv cíclicas de las series de tiempo generadas en un modelo de crecimiento endógeno, ya que este filtro requiere que las series temporales sean estacionarias en diferencias (es decir, procesos I(1)) e impone la existencia de tendencias comunes para las variables no estacionarias, y las series temporales de estos modelos presentan raíz unitaria y están cointegradas. Lo anterior hace que esta técnica de filtrado no sea de uso generalizado9 .
CRITICAS A LAS TÉCNICAS DE FILTRADO
El análisis de las fluctuaciones económicas requiere del uso de técnicas de filtrado que permitan aislar el componente cíclico de las series temporales. Decidir cuál es la técnica más apropiada ha sido un problema en la mayoría de los trabajos de ciclos económicos, incluidos los modelos de CER. Las controversias generadas por esto han originado numerosas investigaciones que muestran cómo la técnica de filtrado empleada en el análisis de los ciclos económicos, puede condicionar en gran medida el tipo de regularidades cíclicas a explicar. Esas investigaciones van dirigidas a los aspectos metodológicos en la evaluación de los modelos de CER, especialmente a la forma como los modelos teóricos corroboran los resultados del fenómeno observado. En particular, algunas de ellas se refieren al uso generalizado del filtro de Hodrick y Prescott (1980) en los modelos de CER como los de Kydland y Prescott (1982) y Hansen (1985).
Entre los trabajos que cuestionan el problema citado está el de Baxter (1991). Para este autor no todos los hechos estilizados son robustos con respecto al método de filtrado empleado y las variaciones más significativas se dan en el comportamiento cíclico de las horas trabajadas y la productividad. Por su parte, King y Rebelo (1993) muestran que el filtro de HP aplicado a grandes muestras contiene una diferencia de orden cuatro centrada y entrega series de tiempo que son estacionarias en diferencias; además muestran que la aplicación de este filtro a series de Estados Unidos y a series generadas mediante modelos de CER lleva a cuestionar su uso generalizado como método de eliminación de la tendencia. Asimismo, utilizando varios ejemplos concluyen que este filtro puede alterar drásticamente las medidas de persistencia, variabilidad y comovimientos.
Harvey y Jaeger (1993) utilizando modelos estructurales de series de tiempo, que permiten tratar explícitamente los movimientos estacionales e irregulares que pueden distorsionar los componentes cíclicos estimados, analizan las consecuencias del filtro de HP. Para ellos citando a Blanchard y Fischer (1989), caracterizar los hechos estilizados asociados a un conjunto de series de tiempo, es una etapa crucial en la investigación macroeconómica; por tanto, para que tales hechos sean útiles deben ser consistentes con las propiedades estocásticas de los datos y presentar información relevante. Así, la aplicación mecánica del filtro HP puede conducir a los investigadores a reportar resultados espurios del comportamiento cíclico de los datos.
Cogley y Nason (1995) reseñan trabajos previos y analizan los efectos del filtro HP cuando es aplicado a series de tiempo estacionarias en diferencias (ED) y en tendencia (ET), porque muchos de los trabajos que utilizan HP asumen que los datos originales son estacionarios, supuesto que es problemático debido a que el filtro generalmente es aplicado a datos no estacionarios. Para cuantificar sus efectos en series temporales sintéticas, utilizan el modelo de ciclos económicos de Christiano y Eichenbaum (1992) aplicado a series de tiempo ED y ET, y ajustado a datos trimestrales de la economía de Estados Unidos para el periodo 1954-1991. De acuerdo con, Cogley y Nason (1995), cuando el filtro HP se aplica a procesos integrados genera periodicidades del ciclo económico y comovimientos aún si no están presentes en los datos originales, luego el filtro puede conducir a resultados espurios, dado que la interpretación de los hechos estilizados depende de los supuestos sobre la naturaleza de la serie. Adicionalmente, los modelos de CER pueden exhibir características del ciclo económico en los datos filtrados con HP, aún si no están presentes en las series prefiltradas10.
Park (1996) compara el filtro de Hodrick Prescott, el filtro de Beveridge-Nelson (BN) y un filtro que asume una tendencia lineal en el tiempo (LIT). El autor muestra que los hechos estilizados de la economía de Estados Unidos son sensibles a la técnica de filtrado empleada, haciendo énfasis en las distorsiones que pueden presentar los hechos estilizados cuando las series agregadas son integradas. También analiza si la sensibilidad de los hechos estilizados, causada por un filtro al extraerle la tendencia a los datos, es simétrica entre los datos observados y los simulados por el modelo.
En el análisis de las propiedades de los filtros Park (1996), además de destacar el resultado de Cogley y Nason (1995), para quienes el filtro de HP aplicado a series prefiltradas integradas de orden uno puede dar lugar a ciclos económicos que no existen en los datos prefiltrados, muestra que este problema se hace más evidente cuando el grado de integración de la serie prefiltrada es mayor. Con el fin de comparar los efectos de los métodos de filtrado, Park (1996) utiliza datos trimestrales de la economía de Estados Unidos correspondientes al periodo 1953:3-1986:3, y series generadas por el modelo de CER de Hansen (1985). Park estudia los segundos momentos relevantes del componente cíclico de los datos observados, extraído con los filtros HP, BN y LIT. Encuentra que la discrepancia más significativa entre los filtros, está relacionada con la variabilidad relativa entre las horas trabajadas y la productividad.
Al comparar los resultados obtenidos con los filtros HP y BN, Park (1996) concluye que: los hechos estilizados de la economía de Estados Unidos son sensibles a la técnica de filtrado empleada; las diferencias entre el filtro HP y los demás filtros parecen ser invariantes si son aplicados a datos simulados u observados; y las distorsiones que causan estos filtros en los hechos estilizados son simétricas en los datos observados y en los datos simulados. También concluye que el uso de una técnica de filtrado y su distorsión de los hechos estilizados puede no implicar necesariamente la invalidación del desempeño de un modelo de CER para replicar la economía estudiada.
De otro lado, Canova (1998) identifica si existe un conjunto de relaciones invariantes en la definición de ciclo empleada e indica situaciones en las cuales la selección de un concepto estándar de ciclo entrega impresiones erróneas de los comovimientos de las variables. Para ello compara las propiedades del componente cíclico de un conjunto de series macroeconómicas de Estados Unidos, que obtiene usando técnicas de filtrado univariadas y multivariadas. Este autor encuentra que desde el punto de vista cuantitativo y cualitativo, los "hechos estilizados" de los ciclos económicos varían ampliamente dependiendo de las técnicas de filtrado utilizadas para aislar la tendencia.
Adicional a las conclusiones de trabajos previos, Canova (1998) encuentra que el filtro HP (para λ = 1.600 produce resultados similares a los obtenidos con el filtro de paso de banda de Baxter y King (1999) y concentra la atención del investigador en ciclos con duración media de 4 a 6 años. Considera, igualmente, que la caracterización empírica de los ciclos económicos que se obtiene con métodos de filtrado multivariados, fundamentados en la teoría económica, es diferente de la obtenida con métodos estadísticos basados en procedimientos univariados. Señala además, cómo la práctica de construir modelos teóricos, cuyas versiones numéricas igualen cuantitativamente un conjunto de regularidades obtenidas con un concepto particular de fluctuación cíclica, amerita una reconsideración. Pese a que muchos trabajos presentaron resultados similares a Canova (1998), es después de la publicación de este artículo cuando se comienza a aceptar que la técnica de filtrado utilizada es relevante para analizar los ciclos económicos.
Basados en la definición de ciclo económico adoptada por la NBER, Baxter y King (1999) proponen un método para extraerlo, en el cual el investigador especifica las características del componente cíclico de la serie. Ellos intentan dar una aproximación a un filtro óptimo, un filtro paso de banda (PB), el cual retenga componentes de los datos con fluctuaciones periódicas entre 6 y 32 trimestres, mientras remueve componentes con frecuencias muy bajas y con frecuencias muy altas. Con ese fin, el filtro utilizado debe cumplir los siguientes requisitos:
1. Debe extraer un rango de periodicidades sin alterar sus propiedades inherentes.
2. No debe producir un movimiento de fase.
3. El método debe ser una aproximación óptima de un filtro ideal.
4. La aplicación de un filtro a series con tendencia debe producir unas series de tiempo estacionarias.
5. El método debe ser independiente de la longitud de la serie.
6. Debe ser de fácil aplicación y uso.
Baxter y King (1999) al comparar su método con otros filtros, en particular con el de HP, en términos de su capacidad para remover raíces unitarias, no introducir cambios de fase y la habilidad para aislar frecuencias del ciclo económico sin ponderaciones de frecuencias pasadas, encuentran que las técnicas de filtrado lineal y de diferencias de primer orden no son adecuadas para extraer el ciclo económico, que el análisis de filtros de media móvil y que el filtro de HP en algunos casos produce aproximaciones razonables a un filtro ideal. Adicionalmente, concluyen que el filtro de paso de banda es más flexible y fácil de implementar, y produce una mejor aproximación al filtro ideal.
Restrepo (2002) analiza los efectos del filtrado de bajas frecuencias en la explicación de las propiedades cíclicas de un modelo, a diferencia de Canova (1998) que estudia la robustez de las propiedades cíclicas observadas con la aplicación de diferentes métodos de filtrado. En su análisis, Restrepo incluye el filtro de Hodrick y Prescott (1980), el filtro paso de banda de Baxter y King (1999) y un filtro en el cual el componente cíclico se obtiene aplicando una descomposición ciclo-tendencia, consistente con la teoría de crecimiento y propuesto por King, Plosser y Rebelo (1988).
Dado que este modelo postula un crecimiento exógeno caracterizado por una tendencia lineal determinista, el componente cíclico utilizando una descomposición teórica (DT) se obtiene extrayendo la tendencia determinista de la serie temporal. El modelo es ajustado a datos de la economía de Estados Unidos para el periodo 1955:3-1994:1. Un aspecto característico de este trabajo son los contrastes entre los estadísticos obtenidos de las series filtradas mediante la DT y los hallados para las series filtradas con HP y PB. En particular, Restrepo (2002) compara las desviaciones estándar que miden la volatilidad de las distintas variables. Para ello utiliza un contraste de comparación de medias para el caso en el que las muestras no son independientes y el contraste Kolmogorov-Smirnov para comparar las distribuciones de frecuencias muestrales de los estadísticos de interés.
Entre los principales hallazgos de Restrepo (2002) se encuentra que:
1. La evaluación de las regularidades cíclicas del modelo, basada en los filtros HP y PB difiere sustancialmente de la descomposición ciclotendencia que deriva el componente cíclico al extraer la tendencia determinista propuesta por el modelo de crecimiento estándar.
2. El contraste de Kolmogorov-Smirnov muestra que estos filtros tienen propiedades muy distintas a las exhibidas por las series generadas por el modelo, una vez ha sido aislada la tendencia determinista.
3. Las conclusiones sobre las características cíclicas del modelo y de los agregados macroeconómicos observados pueden verse afectadas por el filtro elegido.
Igualmente, Restrepo (2002) avanza en el análisis de los efectos de filtrado de bajas frecuencias al mostrar que la elección de la descomposición también condiciona las propiedades cíclicas extraídas del modelo estudiado y los resultados de la evaluación del modelo.
Por su parte, Arango y Castillo (1999) cuestionan hasta qué punto son estilizados los hechos de los ciclos económicos y revisan los resultados que en materia de regularidades se han obtenido para distintos países, períodos, frecuencia de los datos, nivel de desagregación y métodos de eliminación del componente permanente presentados en distintos trabajos. Arango y Castillo (1999), citando a King et al. (1988) señalan la posibilidad de que los hechos estilizados fuesen 3 –sensibles a los métodos usados para aislar la tendencia–, y cómo para Blanchard y Watson (1986), en la presentación de las características de la economía que se busca reproducir por medio de los modelos de CER, la evidencia es mixta porque los hechos observados no siempre coinciden con las predicciones.
De acuerdo con la literatura revisada por Arango y Castillo (1999), las propiedades económicas de los ciclos, en ocasiones, pierden regularidad dependiendo del período, la economía y el proceso de eliminación del componente permanente de las series. La volatilidad del ciclo del producto observado en frecuencia trimestral está alrededor del 2%, siempre que se obtenga por medio del filtro de HP, de otra forma el valor estimado resulta superior.
De otra parte, para estos autores hay algunas señales de alerta con respecto a que los precios no parecen ser contracíclicos cuando la frecuencia de los datos es anual o cuando el filtro utilizado es diferente de HP. La correlación contemporánea es negativa cuando el componente cíclico es obtenido empleando HP para datos trimestrales y el factor de suavización es 1.600. No hay evidencia de que los agregados monetarios sean pro o contracíclicos. Las tasas de interés de corto plazo son, levemente procíclicas, pero las de largo plazo pueden caracterizarse como contracíclicas.
Domenéch y Gómez (2005) consideran que a pesar de las ventajas que caracterizan a los filtros HP y BP éstos tienen algunos problemas. Para citar uno, afirman que al tratarse de métodos univariantes, no utilizan ningún tipo de información contenida en otras variables macroeconómicas que pueda ser útil para distinguir entre perturbaciones transitorias o permanentes.
Citando el trabajo de Trajtenber (2004), las series macroeconómicas necesitan un método simple para remover la tendencia y centrar el análisis sobre las fluctuaciones cíclicas. Enfoque que se justifica si la interacción entre la tendencia y las fluctuaciones cíclicas es pequeña. Aún así, el uso de un procedimiento incorrecto para remover la tendencia puede complicar la separación de la tendencia del ciclo.
A su vez, Vásquez y Restrepo (2009) al emplear el filtro de HP, el filtro paso de banda y una descomposición teórica, derivada del modelo de crecimiento exógeno de King et al. (1988), muestran a través de contrastes estadísticos cómo la evaluación de un modelo del ciclos económicos reales depende del método de filtrado empleado para extraer el componente cíclico de las series temporales. Los autores señalan que las propiedades del componente cíclico estimado con los tres métodos alternativos presentan diferencias estadísticamente significativas; en particular, entre las obtenidas con el filtro de HP y el filtro paso de banda, lo cual difiere del trabajo de Canova (1998).
Finalmente, en el Cuadro 1 se presenta un resumen de los trabajos que analizan algunos de los sesgos introducidos por las técnicas de filtrado.


CONCLUSIONES
A los distintos modelos posteriores al de Kydland y Prescott (1982), apoyados en la teoría del crecimiento económico, y que explican los ciclos económicos con base en choques reales, particularmente choques tecnológicos, se les denomina modelos de CER, como es mencionado en Rebelo (2005). En estos modelos distintos supuestos suelen utilizarse, tales como choques: transitorios o permanentes, endógenos o exógenos, en el precio del petróleo, fiscales o monetarios, divisibilidad o indivisibilidad del factor trabajo, comovimientos o no entre sectores de la economía, entre otros. Si bien hay diferencias en los supuestos y hallazgos de los diferentes trabajos de CER, se puede identificar en la evaluación de los modelos empleados, que el producto es menos volátil que la inversión, pero más que el consumo, y con una volatilidad similar al trabajo (Kydland y Prescott, 1982; Long y Plosser, 1983; King et al., 1988).
En la literatura además de considerarse los choques mencionados, se plantean otras alternativas, tal como lo hace Rebelo (2005), quien propone una guía a futuro para el estudio de los ciclos económicos, siguiendo los lineamientos dados por Prescott (1986) y adicionándole dos nuevos supuestos: los denominados "nuevos choques" o nuevos incrementos en la productividad –debidos al desarrollo de nuevas tecnologías como la Internet– y los choques asociados al impacto que tienen los procesos de innovación sobre la productividad total factorial.
Para los economistas interesados en el estudio de ciclos económicos además del modelo teórico que se debe utilizar, hay dos problemas fundamentales: ¿cómo extraer el ciclo económico? y la falta de un consenso sobre los determinantes de las fluctuaciones económicas. Con respecto a la extracción del ciclo económico, suelen utilizarse técnicas fundamentadas en la teoría económica y otras con base en herramientas de la estadística, empleándose en este último caso análisis en el dominio del tiempo y/o de la frecuencia. Dados los diferentes métodos empleados para la extracción del cíclico de una serie de tiempo económica, es posible obtener distintos hechos estilizados o información del ciclo económico, al emplear una u otra técnica de filtrado. Por otra parte, los distintos métodos pueden condicionar el tipo de regularidades cíclicas a explicar, como lo son las medidas de persistencia, variabilidad y comovimientos de las variables económicas.
Las técnicas de filtrado de series de tiempo económicas como instrumento de análisis dentro de la práctica económica para explicar los ciclos económicos tienen un uso bastante generalizado y "antiguo"; sin embargo, la elección de uno u otro método depende en gran medida, como lo menciona Trajtenberg (2004), del tipo de problema e información que se tenga del mismo. Así, autores como Mitchell (1913, 1927), Burns y Mitchell (1946), Hodrick y Prescott (1980), Kydland y Prescott (1982), Long, Plosser y Rebelo (1983), Hansen (1985), Baxter y King (1999), Restrepo (2002), entre otros, han intentado analizar las características de los distintos agregados económicos, utilizando distintas técnicas de filtrado y enfoques teóricos, con el fin de avanzar en la comprensión del origen de los ciclos económicos y sus consecuencias sobre las economías reales.
NOTAS AL PIE
1 La definición de ciclo económico de Burns y Mitchell es la base de la investigación sobre el ciclo económico que realiza en forma permanente la NBER (National Bureau of Economic Research, EE.UU).
2 De acuerdo con Rebelo (2005), el trabajo de Kydland y Prescott (1982), además de moldear la agenda de investigación macroeconómica de la década de los ochenta y noventa, resultó ser el punto de partida para muchas teorías en las cuales los choques tecnológicos no tenían un rol importante.
3 El supuesto de la indivisibilidad del factor trabajo hace que la investigación de Hansen (1985) difiera de otras similares, como la de Kydland y Prescott (1982).
4 Una serie económica no sólo admite descomposiciones de tipo aditivo, también permite descomposiciones de tipo multiplicativo o combinaciones de ambas. En algunos casos, en la descomposición solamente se consideran los componentes secular y cíclico, porque la serie previamente ha sido desestacionalizada y el componente irregular aislado.
5 Este componente es de poco interés para los investigadores, sin embargo, para realizar algún análisis de la serie económica se requiere aislarlo.
6 Para King et al. (1988), la expresión lineal para la tendencia, representa el progreso técnico aumentativo de trabajo.
7 Para Harvey y Jaeger (1993), el modelo puede ser extendido para trabajar con datos estacionales.
8 El procedimiento de Johansen (1988) permite contrastar si dos o más variables están unidas por una tendencia temporal común. Por tanto, primero se escoge un vector autorregresivo de orden p; luego se realizan una serie de regresiones y se obtienen los residuales, con éstos se calculan los cuadrados de las correlaciones canónicas y; utilizando los cálculos anteriores se realiza el test de la traza. Los resultados se comparan con los estadísticos de la tabla apropiada de Johansen para determinar el número de relaciones de cointegración.
9 Una aplicación de esta técnica se encuentra en el trabajo de Restrepo y Vásquez (2004), en el cual el filtro es utilizado por primera vez para analizar las propiedades cíclicas del modelo de crecimiento endógeno de Uzawa y Lucas.
10 King y Rebelo (1993) caracterizan además una clase de modelos de componentes no observados para los cuales el filtro de HP es el filtro óptimo de Wiener, pero sugieren que son una tipología poco interesante.
REFERENCIAS BIBLIOGRÁFICAS
[1] Arango, L. y Castillo, M. (1999). ¿Son estilizadas las regularidades del ciclo económico? Una breve revisión de la literatura. Borradores de Economía, 115. Bogotá: Banco de la República. [ Links ]
[2] Avella,M. y Ferguson, L. (2003). El ciclo económico. Enfoque e ilustraciones. Los ciclos económicos de Estados Unidos y Colombia. Borradores de Economía, 284. Bogotá: Banco de la República. [ Links ]
[3] Barro, R.J. (1976). Rational Expectations and the Role of Monetary Policy. Journal of Monetary Economics, 2(1), 1-32. [ Links ]
[4] Barro, R.J. (1980). A CapitalMarket in an Equilibrium Business Cycle Model. Econometrica, 48(6), 1393-1417. [ Links ]
[5] Baxter, M. (1991). Business cycles, stylized facts, and the exchange rate regime: evidence from the United States. Journal of International Money and Finance, 10(1), 71-88. [ Links ]
[6] Baxter, M. y King, R. (1995). Measuring business cycles approximate bandpass filter for economic time series. NBER Working Papers Series, 5022. Cambridge: NBER. [ Links ]
[7] Baxter, M. y King, R. (1999). Measuring business cycles: approximate bandpass Filters for economic time series. Review of Economics and Statistics, 81(4), 575-593. [ Links ]
[8] Beveridge, S. y Nelson, C. (1981). A new approach to decomposition of economic time series into permanent and transitory components with particular attention to measurement of the business cycle. Journal of Monetary Economics, 7(2), 151-174. [ Links ]
[9] Blanchard, O. y Fischer, S. (1989). Lectures in Macroeconomics. Cambridge, Massachusetts: MIT Press. [ Links ]
[10] Blanchard, J. y Watson, M. (1986). Are business cycles alike. En Gordon, R.J. (Ed.), The American Business Cycles: Continuity and Change (pp. 123-180). Chicago: University of Chicago Press for NBER. [ Links ]
[11] Bógalo, J., y Quiles, E. (2003). Estimación del ciclo económico mediante métodos de Butterworth. Boletín Trimestral de Coyuntura, 83, 1-20. [ Links ]
[12] Burns, A. y Mitchell, W. (1946). Measuring Business Cycles. Nueva York: National Bureau of Economic Research. [ Links ]
[13] Canova, F. (1998). Detrending and business cycle facts. Journal of Monetary Economics, 41(3), 475-512. [ Links ]
[14] Christiano, L. y Eichenbaum, L. (1992). Current Real Business Cycle Theories and Aggregate Labor Market Fluctuations. American Economic Review, 82(3), 430-450. [ Links ]
[15] Clark, P. K. (1987). The cyclical component of U.S. economic activity. Quarterly Journal of Economics, 102(4), 797-814. [ Links ]
[16] Cogley T. y Nason, J. (1995). Effects of Hodrick and Prescoot Filter on Trend and Difference Stationary Time Series: Implication for Business Cycle Research. Journal of Economic Dynamics and control, 19(1-2), 253-278. [ Links ]
[17] Domenéch, R. y Gómez, V. (2005). Ciclo económico y desempleo estructural en la economía española. Investigaciones económicas, 39(2), 259-288. [ Links ]
[18] Friedman, M. (1968). The role of monetary policy. American Economic Review, 58(1), 1-17. [ Links ]
[19] Gómez, V. y Bengoechea, P. (2000). Estimación del componente cíclico de las series económicas: Una aplicación a los indicadores de clima e índices de producción industrial. Investigaciones económicas, 24(2), 473-485. [ Links ]
[20] Gonzalo, J. y Granger, C. (1995). Estimation of common long-memory components in cointegrated systems. Journal of Business and Economic Statistics, 13(1), 27-35. [ Links ]
[21] Guerrero, V. M. (2008). Estimating trends with Percentage of Smoothness Chosen by the User. International Statistical Review, 76(2), 187-202. [ Links ]
[22] Hansen, G. (1985). Indivisible Labor and the Business Cycle. Journal of Monetary Economics, 16(3), 309-327. [ Links ]
[23] Harvey, A. y Jaeger, A. (1993). Detrending, stylized facts and the business cycle. Journal of Applied Econometrics, 8(3), 231-247. [ Links ]
[24] Hodrick, R. y Prescott, E. (1997). Post-War U.S. business cycles: an empirical investigation. Journal of Money, Credit and Banking, 29(1), 1-16. [ Links ]
[25] Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economics Dynamics and Control, 12(2), 231-258. [ Links ]
[26] Issler, J. V., Arinos, A. y Teixeira, O. (2008). The welfare cost of macroeconomic uncertainty in the post-war period. Economics Letters, 98(2), 167-175. [ Links ]
[27] Lucas, R.E. Jr. (1972). Expectations and the neutrality of money. Journal of Economic Theory, 4(2), 103-124. [ Links ]
[28] Kalman, R. E. (1960). A new approach to linear filtering and prediction theory. Transactions, of the ASME, Journal of Basic Engineering, 82(D), 35-45. [ Links ]
[29] King, R., Plosser, C. y Rebelo, S. (1988). Production, Growth and Business Cycles: I. Journal of Monetary Economics, 21(2-3), 195-232. [ Links ]
[30] King, R., Plosser, C., Stock, J. y Watson, M. (1991). Stochastic trend and economic fluctuations. American Economic Review, 85(4), 819-840. [ Links ]
[31] King, R. y Rebelo, S. (1993). Low Frequency Filtering and Real Business Cycles. Journal of Economics Dynamics and Control, 17(1-2), 207-231. [ Links ]
[32] King, R. y Rebelo, S. (2000). Resuscitating real business cycles. Working Paper Series, 7534. Cambridge, MA: National Bureau Economic Research. [ Links ]
[33] Kohn, R., Ansley, C.F. yWong, Ch.M. (1992). Non-parametric spline regression with autoregressive moving average errors. Biometrika, 79(2), 335-346. [ Links ]
[34] Kydlan, F. y Prescott, E. (1982). Time to Build and Aggregate Fluctuactions. Econometrica, 50(6), 1345-1370. [ Links ]
[35] Lee, T.C. (2003). Smoothing parameter selection for smoothing splines: a simulation study. Computational. Statistics & Data Analysis, 42(1-2), 139-148. [ Links ]
[36] Long, J. y Plosser, C. (1983). Real Business Cycles. Journal of Political Economy, 91(1), 39-69. [ Links ]
[37] Mitchell, W. (1913). Business Cycles. Berkeley: University of California Press. [ Links ]
[38] Mitchell, W. (1927). Business Cycles: The Problems and Its Setting. New York: National Bureau Economic Research. [ Links ]
[39] Moral, J. (2000). Introducción al tratamiento de series temporales mediante filtros. (Tesis inédita de doctorado). Universidad Autónoma, Madrid. [ Links ]
[40] Morley, J. (2010). The two interpretations of the Beveridge-Nelson decomposition. Macroeconomic Dynamics, 1-21. doi: 10.1017/S1365100510000118. [ Links ]
[41] Nelson, C. y Plosser, C. (1982). Trends and random walks in macroeconomic time series: some evidence and implications. Journal of Monetary Economics, 10(3), 139-162. [ Links ]
[42] Park, G. (1996). The Role of Detrending Methods in a Model of Real Business Cycles. Journal of Macroeconomics, 18(3), 479-501. [ Links ]
[43] Prescott, E. (1986). Theory ahead of business cycles measurement. Carnegie - Rochester Conference Series of Public Policy, 25, 11-66. [ Links ]
[44] Quah, D. y Sargent, T. (1992). A dynamic index for large cross sections. Discussion Paper, 77. Minneapolis: Federal Reserve Bank of Minneapolis. [ Links ]
[45] Rebelo, S. (2005). Real business cycle models: past, present, and future. Scandinavian Journal of Economics, 107(2), 217-238. [ Links ]
[46] Restrepo, S. (2002). Análisis de las propiedades cíclicas y tendenciales en el marco de dos modelos estándar de crecimiento. (Tesis inédita de doctorado), Universidad del País Vasco, España. [ Links ]
[47] Restrepo, S. y Vázquez, J. (2004). Cyclical features of the Uzawa-Lucas endogenous growth model. Economic Modelling 21(2), 285-322. [ Links ]
[48] Ruiz, J. (2002). Una nota metodológica acerca de aplicaciones del filtro de Kalman a las calibraciones en modelos de ciclo real. Investigaciones Económicas, 26(2), 35-57. [ Links ]
[49] Scott, A. (2000). A multivariate unobserved Components model of cyclical activity. Discussion Paper Series, DP2000/04. New Zealand: Reserve Bank of New Zealand. [ Links ]
[50] Solera, A. (2003). El filtro de Kalman. Managua: Banco Central de Costa Rica. [ Links ]
[51] Stock, J. y Watson, M. (1988). Testing for common trends. Journal of the American Statistical Association, 83(404), 1097-1107. [ Links ]
[52] Stock, J. y Watson, M. (1989). New index of coincident and leading indicators. En Blanchard, O. J. & Fischer, S. (Ed.), Series - NBER Macroeconomics Annual (pp. 351-393). Cambridge: The MIT Press. [ Links ]
[53] Trajtenberg, L. (2004). Modelización de ciclos y tendencias en series de tiempo macroeconómicas Argentina: 1980-2000. Asociación Argentina de Economía Política. Anales/ Buenos Aires. Recuperado de http://www.aaep.org.ar/anales/works/works2004/Trajtenberg.pdf. [ Links ]
[54] Vásquez, F. y Restrepo, S. (2009). Efectos de las técnicas de filtrado en la evaluación de un modelo de ciclos económicos reales. Lecturas de Economía, 71(2), 43-76. [ Links ]













 [1]
[1] 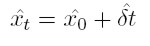 [2]
[2]  [3]
[3]  [4]
[4]  [5]
[5] 
