Inés María Ulloa Villegas^*

^*Magíster en Economía, se desempeña actualmente como profesor del Departamento de Economía de la Universidad del Valle (Cali, Colombia). E-mail: jorge.uribe@correounivalle.edu.co. Dirección de correspondencia: Carrera 13 N. 100-00, edificio 387, oficina 3014 (Cali, Colombia).

^*Diplom Volkswirtin, se desempeña actualmente como Profesora Asociada del Departamento de Economía de la Universidad del Valle (Cali, Colombia). E-mail: ines. ulloa@correounivalle.edu.co. Dirección de correspondencia: Calle 13 N. 100-00, edificio 387, oficina 4020 (Cali, Colombia).

Los autores agradecen el apoyo de la Facultad de Ciencias Sociales y Económicas y del Centro de Investigaciones y Documentación Socioeconómica (CIDSE); la invaluable asistencia de investigación de Stephanía Mosquera López y Natalia Restrepo López; y los comentarios de dos árbitros anónimos de la revista.

Este artículo fue recibido el 5 de octubre de 2010, la versión ajustada fue remitida el 18 de marzo de 2011 y su publicación aprobada el 4 de abril de 2011.

Resumen

En este documento se revisa la relación teórica entre eficiencia informacional y eficiencia en la asignación. Igualmente, se proponen dos mejoras a la metodología empírica tradicional para medir la eficiencia en el sentido débil. La primera consiste en calcular el estadístico de eficiencia dinámicamente, lo cual enriquece el análisis y permite definir intervalos con distintos grados de eficiencia en el mismo mercado. La segunda pretende evaluar la eficiencia a través de cópulas, las cuales son robustas ante la no normalidad y la no linealidad que exhiben las series de tiempo financieras.

Palabras clave: eficiencia financiera, razones de varianza, cópulas, independencia. JEL: G14, D53, C15, C18, C58.

Abstract

The theoretical relationship between informational efficiency and efficiency in the assignment is reviewed in this document. Two improvements are proposed with respect to the traditional empirical methodology that is currently used to test market efficiency in the weak form. The first one is to calculate the statistic to measure efficiency dynamically. This strategy enriches the analysis and allows the reader to define intervals with different degrees of efficiency in the same market. The second one is an efficiency measure based upon copulas, which are robust in accommodating both non normality and non linearity (common features observed in financial data).

Key words: financial efficiency, variance rates, copulas, independence. JEL: G14, D53, C15, C18, C58.

Rèsumè

Dans ce document on revisite la relation théorique entre l´efficacité informationnelle et l'efficience dans l'allocation des ressources. Également, on propose deux améliorations à la méthodologie empirique traditionnelle pour mesurer l'efficience dans le sens faible. La première consiste à calculer la valeur statistique d'efficience dynamiquement, ce qui enrichit l'analyse et permet de définir des intervalles avec des degrés distincts d'efficience dans le même marché. La deuxième a pour but d´évaluer l'efficience à travers de couples qui sont stables et robustes face à la non normalité et la non linéarité des séries temporelles financières.

Mots clés : efficience financière, taux de variabilité, couples. JEL: G14, D53, C15, C18, C58.

Desde que Eugene Fama (1970) acuñó el famoso término de “eficiencia de mercados” para referirse a los procesos aleatorios que se comportan como “juegos justos”, cuyos resultados no pueden ser predichos sistemáticamente, los alcances y las implicaciones teóricas y políticas del mismo han sufrido devenires de todo tipo. Las posiciones académicas con respecto a la eficiencia en este sentido son contrastantes y la han convertido en una acepción más de la misma controversia que se extiende a lo largo y ancho del pensamiento económico contemporáneo, entre economistas neokeynesianos y neoclásicos, que difieren en último término sobre el papel que el Estado debe jugar en una economía de mercado.

En un lado del espectro se sitúan quienes creen fehacientemente en la eficiencia de los mercados financieros, – por ejemplo, Fama y French (2010), Fama (1991, 1998), Malkiel (1999, 2003, 2005), entre otros –, los cuales han desarrollado un arsenal estadístico enorme para “probar” dicha eficiencia. La implicación política de esta posición será, regularmente, que los mercados de capitales son eficientes y constituyen un mecanismo óptimo para la asignación de recursos; por tanto, la intervención estatal sólo puede empeorar las cosas.

En el otro lado están quienes no creen en la eficiencia del mercado y de hecho niegan que dicha eficiencia sea posible (Grossman y Stiglitz, 1980; Stiglitz, 2010), por lo cual el papel del Estado, por ejemplo a nivel regulatorio, no sólo tiene cabida sino que es imprescindible.

También se pueden encontrar quienes consideran este concepto de eficiencia sólo como un artificio ideológico propio de la arremetida neoclásica para justificar las políticas de libre mercado, en la década de los setenta, que por ende nada tiene que ver con la eficiencia económica en el sentido tradicional, es decir, en el sentido de Pareto (Hyme, 2003). En este caso extremo la eficiencia de los mercados financieros no tiene ninguna implicación de política económica, sólo se trata de un término prejuiciado.

Finalmente, un enfoque alternativo que crítica las aproximaciones tradicionales a la medición de la dependencia en las series financieras y en alguna medida sus implicaciones sobre la Hipótesis de los Mercados Eficientes (HME) se encuentra, por ejemplo, en los trabajos de Peters (1996) y Mandelbrot y Hudson (2006).

En este trabajo se aborda el tema de la eficiencia del mercado una vez más y se señalan algunas de las implicaciones teóricas del mismo. Primero, se plantea que la eficiencia en el sentido informacional es una condición necesaria para la eficiencia en la asignación y con este argumento teórico en mente se procede al análisis empírico de la eficiencia, para varios mercados de acciones en el mundo. En este marco empírico se plantean algunas mejoras metodológicas a las medidas tradicionales.

De esta forma es como en la primera parte del documento se argumenta que la eficiencia en la información (o en el sentido de Fama), debe ser entendida como una condición necesaria, aunque no suficiente, para que se cumpla el Primer Teorema del Bienestar de la Economía Walrasiana. Se subraya así, un salto teórico enorme que muchas veces se pasa por alto: para que un mercado sea eficiente en el sentido de Pareto, primero debe serlo informacionalmente; no obstante, no es necesariamente cierto que un mercado eficiente en el sentido de Fama lo es automáticamente en el sentido de Pareto. Esta idea también fue esbozada por Stiglitz (1981) y no ha tenido la atención que se esperaría dentro de la literatura académica, pero vuelve a ser particularmente relevante en épocas de crisis.

Lo anterior se ilustra con una breve revisión de dos trabajos clásicos sobre la materia: que los mercados nunca pueden ser eficientes informacionalmente (en el sentido fuerte), idea que fue desarrollada por Grossman y Stiglitz (1980), y que esta ineficiencia, que a su vez es producto de la presencia de información asimétrica, implica que los equilibrios del mercado competitivo ya no están garantizados, en particular no se puede asegurar que se cumplan los dos teoremas del bienestar fundamentales del equilibrio walrasiano (Rothschild y Stiglitz, 1976).

En este trabajo se plantea que la eficiencia de mercado no deja de ser una condición deseable, toda vez que un mercado eficiente estará reflejando mejor la información disponible sobre los precios de los activos financieros y su valor fundamental. Lo que sucede es que no constituye en ningún caso un argumento definitivo, por sí solo, en términos de política económica. De la anterior discusión deberá quedar claro que, también, es un error considerar que los dos conceptos (en el sentido de Fama y en el sentido de Pareto) no tienen relación alguna como se plantea en Hyme (2003).

De esta forma, sobre la base de que la eficiencia es una propiedad deseable, aunque no concluyente, se procede al análisis estadístico. Se estiman las medidas de eficiencia (débil), del mercado propuestas por la literatura contemporánea, para varios índices latinoamericanos y del mundo, de forma dinámica. Se subrayan las limitaciones teóricas y prácticas de las mismas, y se propone una forma alternativa de medición basada en las cópulas, una opción que es más robusta empíricamente. Este análisis permite establecer que incluso desde las propuestas estándar que existen para medir la eficiencia, es posible identificar indicios de ineficiencia en los mercados que tienden a sobre reaccionar ante las buenas y malas noticias, es decir, aquellos en los que las burbujas de los precios de los activos financieros se han convertido en un comportamiento recurrente en épocas recientes. Este es el caso de los mercados financieros más profundos del mundo: Londres y Nueva York.

Lo anterior deja cabida para la regulación estatal que busca evitar las burbujas financieras, o por lo menos, que busca “desinflarlas” cuando éstas se producen. Este argumento se suma al debate contemporáneo sobre la necesidad de incorporar objetivos sobre los precios de los activos financieros y no únicamente objetivos de inflación de precios al consumidor por parte de las autoridades monetarias. En este contexto, convendría construir medidas dinámicas sobre la eficiencia como las que se proponen en este documento. La condición más laxa que se puede pedir a los mercados financieros es que sean eficientes en el sentido de Fama, y en particular débilmente, y muchas veces ni siquiera a este nivel lo son. Las expectativas juegan aquí un papel fundamental, en particular las expectativas que se retroalimentan. Son estos procesos los que en muchos casos impiden que los mercados ajusten sus precios “eficientemente”, aun si los agentes tienen expectativas racionales. Esta consideración no es original, en últimas es consecuencia de los mismos espíritus animales de los que habló Keynes hace más de 70 años.

UNA REVISIÓN TEÓRICA DEL CONCEPTO DE EFICIENCIA

A market in which prices always fully reflect available information is called efficient (Fama, 1970, 383).

A capital market is said to be efficient if it fully and correctly reflects all relevant information in determining security prices. Formally, the market is said to be efficient with respect to some information set, , if security prices would be unaffected by revealing that information to all participants. Moreover, efficiency with respect to an information set, , implies that it is impossible to make economic profits by trading on the basis of (Malkiel, 1987, 120).

Estas dos definiciones son estándar en la literatura sobre el tema. La segunda es un intento de llevar la primera al campo empírico y evitar las ambigüedades que ésta engendra. No obstante, como ocurre cada vez que una hipótesis se hace más específica, hay cierta pérdida de información con respecto a la que se quería expresar en un principio. La definición de Malkiel (1987) plantea que la eficiencia se puede reducir a la imposibilidad de realizar ganancias sistémicas en el mercado.

La idea subyacente es clara: dado que la información que llega al mercado es abundante (incluso ilimitada) y que en todo momento los precios absorben tal información, si algún hecho del mañana no se ha reflejado en los precios de hoy es porque su materialización depende del azar o porque es desconocido por todos. Si un mercado de capitales es eficiente, será imposible predecir sistemáticamente los precios de los activos que se transan en su interior y, por tanto, obtener ganancias no acotadas sistemáticamente con base en tales activos, siguiendo cualquier tipo de técnica de predicción o haciendo uso de cualquier conjunto de información. El mejor pronóstico del precio mañana será el precio de hoy, el cual corresponde a la suma descontada de los flujos futuros infinitos, representados por la tenencia del activo financiero para su poseedor.

Al reflexionar sobre lo anterior, se observa que no hay discrepancia entre la bolsa pensada como un casino (Stiglitz, 2010) y la bolsa entendida como un mercado cuyo mecanismo de precios refleja toda la información disponible (Fama, 1970). La idea es que el precio responderá a sus fundamentales y cualquier desviación de estos debe ser aleatoria (un casino).

El problema con lo anterior es que no es fácil determinar qué parte de los precios responde a los fundamentales y qué parte no. Por ejemplo, recientemente se creía que el alza del precio de las acciones en los Estados Unidos durante la década de los noventa y principios del siglo XXI, hasta el momento en que estalló la crisis de las “punto com” en el 2002; o desde esa fecha hasta la caída de Lehman Brothers en septiembre de 2008, estaba sustentada en gran medida por los fuertes procesos de innovación tecnológica en esos periodos. Innovación tecnológica, primero por parte de las empresas de nuevas tecnologías de información y después, por parte de los bancos de inversión. Dado lo anterior, era natural concluir que tal ascenso respondía a los fundamentales de las empresas en bolsa. Hoy es evidente que esto no era del todo cierto y que gran parte del alza en los precios bursátiles fue producto del exceso de liquidez presente en el mercado y de la subvaloración del riesgo; es decir, no era producto de los fundamentales, sino de la especulación, era una burbuja.

El ejemplo anterior ilustra un poco las dificultades técnicas y teóricas que existen para discernir si un mercado es eficiente o si no lo es. El problema se hace aún mayor cuando se consideran las características técnicas de las medidas empíricas diseñadas para tal fin: éstas se basan en el análisis de las autocorrelaciones de las series y en la posibilidad de determinar patrones en las mismas que implicarían que existe cierta información que no es recogida por el mercado de forma inmediata, tal como implica la Hipótesis de los Mercados Eficientes (HME). De ahí que una buena forma de medir la eficiencia sea analizando estas autocorrelaciones de las series o, alternativamente, cualquier modelo de predicción contra la estrategia de comprar y mantener.

Llegado este punto se hacen evidentes al menos dos saltos teóricos. Primero, se pasó de la necesidad de determinar si los precios incorporan toda la información disponible de forma inmediata a verificar si era posible realizar ganancias sistemáticas (o “morder al mercado”). Segundo, se trata de verificar dicha posibilidad basándose en el análisis de las relaciones lineales de la serie consigo misma. El primer salto es relativamente fácil de atenuar si se revisa con mayor profundidad el concepto de eficiencia; sobre el segundo hace falta desarrollar nuevas medidas, una de las cuales se propone en este documento.

Con respecto al primer punto se debe tener presente que la imposibilidad de ganarle al mercado sistemáticamente y la incorporación en los precios de toda la información disponible, no es lo mismo; lo primero es una implicación de lo segundo. Sin embargo, puede darse el caso de que no sea posible realizar ganancias sistemáticas basándose en el análisis de autocorrelación y aun así de que exista cierta información que no sea correctamente reflejada por los precios de los activos; por ejemplo, si se utiliza para la predicción un modelo de series de tiempo con un desempeño muy pobre por fuera de muestra, pero con coeficientes individuales estadísticamente distintos de cero.

De cualquier forma, las medidas basadas en el análisis de la autocorrelación son (tal vez por accidente) robustas ante esta crítica, ya que en caso de que los precios reflejen toda la información disponible (independientemente de que se pueda hacer dinero con el modelo estimado), tales correlaciones no deberían existir. En este sentido el análisis de autocorrelación es más válido que el de comparar estrategias de inversión para medir la eficiencia, ya que hace énfasis directamente en lo que se quiere medir y no en su consecuencia.

Nótese algo más, en un mercado “sospechosamente” alcista, como el que es típico cuando se está inflando una burbuja financiera, la autocorrelación tiende a hacerse significativa. Igual sucede con un mercado bajista, que es el típico una vez la burbuja estalla¹. Este patrón no se manifiesta con la misma intensidad en todos los mercados. Ninguna de estas situaciones es producto de los movimientos de los fundamentales de los activos financieros; son, por el contrario, fruto de diversos factores como la especulación, la exuberancia irracional, los espíritus animales o la histeria del inversionista, por ejemplo.

En los dos casos anteriores las medidas de eficiencia basadas en la autocorrelación deberían advertir sobre las sospechosas tendencias del mercado y en efecto lo hacen (ver sección 3). La mala noticia para el inversionista es que, aun cuando se con-cluya que el mercado no es eficiente, esto no garantizará que sea posible “morder al mercado” en todo momento. Más aún, en un mercado alcista los agentes que tienen posiciones largas en los títulos tienden a ganar sistemáticamente y en un mercado bajista los agentes que tiene posiciones cortas también tienden a ganar sistemáticamente, y ambos procesos se retroalimentan y se convierten en profecías auto realizadas, de forma tal que cada vez es más difícil encontrar contrapartes para la transacción. Por supuesto, esto es cierto hasta que el proceso se invierta y las ganancias se acoten, y si el proceso tarda mucho en invertirse debe dudarse de la eficiencia del mercado.

Aquí se pone de manifiesto el alcance de las medidas de eficiencia, más allá de la órbita del inversionista. Este punto es de suma importancia para el regulador, cuyo objetivo no es realizar ganancias especulativas, sino garantizar que los ciclos bajistas y alcistas del mercado respondan en mayor medida a los fundamentales económicos y no a la pura especulación, dados los altos costos que las crisis financieras representan para el bienestar social.

La eficiencia mejor pensada en términos relativos

Un punto más que hace parte del análisis estándar sobre eficiencia es que ésta se puede pensar mejor en términos relativos; es decir, ante algún tipo de información (Campbell, Lo y MacKinlay, 1997). Una taxonomía muy frecuente es la propuesta por Roberts (1967):

1. Eficiencia en el sentido débil: el conjunto de información contra el cuál se plantea la eficiencia del mercado incluye únicamente la historia de los precios o los retornos.

2. Eficiencia en el sentido semi-fuerte: el conjunto de información incluye toda la información conocida por todos los participantes del mercado (información pública disponible).

3. Eficiencia en el sentido fuerte: el conjunto de información incluye toda la información conocida por algún participante del mercado (información privada).

El enfoque que se basa en el estudio de las relaciones de dependencia temporal es adecuado para la eficiencia en el sentido débil. Por su parte, la eficiencia en el sentido fuerte se encuentra inmersa en una paradoja ineludible, que fue señalada por Grossman y Stiglitz (1980)² y que se explicará con mayor detalle más adelante. Hechas estas claridades, como se verá, el solo análisis de la eficiencia débil es lo suficientemente rico para mostrar la imposibilidad de los mercados de comportarse según predice la HME.

Eficiencia en el sentido de Pareto versus eficiencia en el sentido de Fama

En este apartado se relacionan teóricamente la idea de la eficiencia en el sentido de Fama (informacional) con la eficiencia en el sentido de Pareto. Para lo anterior se hará referencia al clásico artículo de Rothschild y Stiglitz (1976) en el cual extienden intuitivamente el concepto de Equilibrio General Walrasiano al caso en que los agentes que intervienen en el mercado cuentan con distintos conjuntos de información. En este estudio los autores encuentran que las características tradicionales del Equilibrio GeneralWalrasiano (EGW) no se mantienen en estos casos, en particular, no se conserva el Primer Teorema del Bienestar.

El resultado de Arrow y Debreu (1954) sobre la existencia del equilibrio general plantea que siempre existe un vector de precios de equilibrio que vacía el mercado. Formalmente, siguiendo a Jehle y Renny (2001): si se considera una economía (uⁱ, eⁱ, θ ^ij , Y ^j) i∈I, j∈J ), en la cual Y^j y uⁱ satisfacen los supuestos usuales³. Y en la que se cumple que para algún vector de producción agregado , entonces, existirá al menos un vector de precios p* >> 0, tal que z(p*) = 0. uⁱ es la utilidad del consumidor i, eⁱ es la dotación inicial del consumidor i (con I consumidores), Y ^j es la función de producción de la empresa j (con j empresas), θ^ij es la porción de los beneficios generados por la empresa j que le corresponde al consumidor i, y, finalmente, z(p*) es el vector de excesos de demanda a los precios de equilibrio p*.

Este vector de precios p* de equilibrio da lugar a asignaciones que se encuentran en el núcleo de la economía, es decir, que son eficientes en el sentido de Pareto (no es posible mejorar el resultado de la asignación walrasiana para algún agente en el mercado, sin disminuir el bienestar de algún otro). Lo anterior es, por supuesto, el Primer Teorema del Bienestar del EGW.

Al respecto Rothschild y Stiglitz (1976) muestran cómo la incertidumbre por sí sola no invalida los resultados clásicos del EGW. En particular, ya no será posible trabajar con funciones de utilidad bajo certeza, sino con funciones de utilidad esperada, las cuales fueron propuestas por von Neumann y Morgenstern (1944),pero los resultados de equilibrio continuarán inalterados. No obstante, una vez se rompe el supuesto de información simétrica y se permite que algunos agentes en el mercado tengan información distinta a la de los demás⁴, sólo existe una forma en la que se sostiene el Primer Teorema del Bienestar: la situación en la que todos los agentes comparten iguales preferencias por el riesgo. De lo contrario, basta con que existan dos tipos distintos de agentes para que los resultados de equilibrio del mercado lleven a asignaciones que pueden no ser eficientes en el sentido de Pareto.

El trabajo subraya entonces la imposibilidad de garantizar que los precios reflejen siempre toda la información disponible, cuando los agentes toman sus decisiones con base en diferentes conjuntos de información. De hecho es este impedimento el que lleva a que los equilibrios de separación o de agrupamiento que deberían operar en estos casos no funcionen, y el equilibrio del mercado muchas veces podría corresponder a la desaparición del mercado.

Nótese la relación directa que hay entre la eficiencia informacional y la eficiencia en el sentido de Pareto⁵. La primera es condición necesaria, más no suficiente para garantizar la segunda. La palabra garantizar en el párrafo anterior enfatiza en que existen algunos casos, poco probables, en los que ciertas configuraciones del mercado lleven a un equilibrio en el cual se cumpla el Primer Teorema del Bienestar, aun bajo información asimétrica. La condición sigue sin ser suficiente, porque incluso cuando el mecanismo de precios opere eficientemente en el sentido informacional, pueden existir rigideces en el corto plazo que impidan su adaptación.

Sobre la imposibilidad de la eficiencia informacional (en el sentido fuerte)

Otro trabajo de Stiglitz, ahora con Grossman (Grossman y Stiglitz, 1980) subraya una falla más de la HME. El argumento general es el siguiente: si se parte del supuesto de que la información es costosa y los mercados son eficientes, entonces nadie tendrá incentivos para incurrir en el costo de la información. Será más rentable y, por ende, un comportamiento racional, esperar a que los precios reflejen toda la información disponible, incluida aquella que es costosa. No habrá que esperar mucho en todo caso, porque la HME garantiza que esta información se incorpore en el precio instantáneamente. No obstante, puesto que todos los agentes tienen los mismos incentivos, ninguno incurrirá en el costo de la información, razón por la cual será imposible que los precios la reflejen.

Esta paradoja opera en particular contra la HME definida en el sentido fuerte: bien los mercados son eficientes o bien la información es costosa. No obstante, puede argumentarse (Fama, 1991) que ésta no invalida la hipótesis en el sentido débil o semi-fuerte (ya que en estos se supone que la información no es costosa).

Las repercusiones de esta paradoja son más hondas de lo que parece a primera vista. Si se anula la eficiencia de mercados en el sentido fuerte, se anula el resultado de la eficiencia informacional y se elimina la garantía teórica de que se llegará a una situación de equilibrio en la cual se cumpla el Primer Teorema del Bienestar.

De lo anterior se desprende que el análisis de la eficiencia debería concentrarse en las alternativas débil y semi-fuerte. En este trabajo se pretende explorar la eficiencia de los mercados en el sentido débil, lo cual puede servir para alertar al regulador sobre fallas informacionales persistentes de los mercados. No obstante, si se encuentra que los mercados son eficientes en el sentido débil, en ningún caso deberá ser tomado como prueba de que el mercado es eficiente en el sentido de Pareto (para eso debería serlo en el sentido fuerte).

SOBRE CAMINATAS ALEATORIAS Y JUEGOS JUSTOS

La contraparte empírica de estos precios que se determinan aleatoriamente son los procesos de caminatas aleatorias o más generalmente las martingalas.

Una martingala es básicamente un juego en el que nadie posee algún tipo de ventaja y en el que la evolución de las ganancias es aleatoria. En estos es imposible inferir el valor futuro del precio utilizando cualquier tipo de estimador lineal o no lineal y el valor esperado de los retornos es cero, condicionado a la historia del juego.

Aunque las martingalas subyacen a cualquier tipo de medición de la eficiencia, los instrumentos más utilizados en las pruebas de este tipo son las caminatas aleatorias que son más específicas que éstas. Una caminata aleatoria puede ser descrita por el siguiente proceso:

[1]

Siendo μ el cambio esperado en el precio o la deriva y ε_t un término de perturbación o incremento esperado en el precio del activo, que se distribuye, según lo restringida que sea la hipótesis que se quiere probar de caminata aleatoria, así:

• Caminata aleatoria tipo 1 (RW1) : ε_t ∼ IID(0, σ²) es un proceso independiente e idénticamente distribuido.
• Caminata aleatoria tipo 2 (RW2) : ε_t ∼ INID (0, σ²), es un proceso independiente, pero no idénticamente distribuido.
• Caminata aleatoria tipo 3 (RW3) : ε_t es un proceso que no es independiente, ni está idénticamente distribuido, pero cuya autocorrelación serial en niveles es igual a cero; es decir, alberga casos como: Cov (ε_t, ε_s) = 0∀t ≠= s, pero en donde Cov(ε²_t, ε²_s ) ≠= 0∀t ≠= s. En otras palabras, puede haber dependencia, pero no correlación.

Cada una de estas hipótesis (RW1, RW2 y RW3) es más laxa que la anterior y en la práctica los estadísticos de eficiencia utilizados casi siempre se refieren a la tercera hipótesis (RW3). También es usual suponer normalidad en la distribución de los residuos y log-normalidad de la variable explicada, para simplificar el análisis y la estimación. Por lo anterior, conviene trabajar sobre los logaritmos de los precios (que se denotarán en adelante con letras minúsculas) y no sobre los precios en niveles, ya que dada la forma de la distribución normal estándar, sería teóricamente posible el caso de precios negativos. La siguiente es la versión en logaritmos de la ecuación de precios.

[2]

En este documento se plantea una alternativa para el cálculo del RW2, que permitirá acercarse a lo que se pretende modelar teóricamente. En pocas palabras se trascienden los paradigmas de la linealidad y la normalidad, que no están justificados en el análisis de eficiencia.

Pruebas empíricas estándar

Una vasta cantidad de pruebas se ha desarrollado para verificar que los precios de las acciones en bolsa siguen caminatas aleatorias. El estudio de la eficiencia de mercado se remonta a Bachelier (1900) y pasa por los trabajos de Working (1934), Kendall (1953), Samuelson (1965), Mandelbrot (1966) y Fama (1970), por mencionar unos pocos. Asimismo, los estadísticos propuestos incluyen los análisis de secuencias, reversas y corridas; las reglas de filtreo; el análisis técnico; el análisis de autocorrelación; la razón de varianzas; las inferencias para horizontes largos de tiempo; el rango de dependencia de largo plazo; entre otros. Los más usuales, el análisis de autocorrelación a través del estadístico Q de Box y Pierce (1970) y las razones de varianza desarrolladas por Lo y MacKinlay (1988).

Análisis de autocorrelación

Se parte de que bajo la hipótesis de RW todas las autocorrelaciones seriales son cero. Un test útil para probar este hecho es el estadístico Q de Box y Pierce (1970) – en general estadístico de Pormanteau –, dado por la siguiente ecuación:

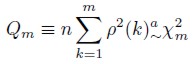[3]

O la versión de Ljung y Box (1978) que es más robusta en muestras pequeñas:

[4]

En esta ecuación, n es el número de observaciones, k el contador de la sumatoria, mel rango en el que se mide la autocorrelación, ρ el coeficiente de autocorrelación y la letra griega χ²_m indica la distribución que sigue el estadístico (con m grados de libertad). La hipótesis nula en este caso es que todas las autocorrelaciones son cero, de modo que si se rechaza lo que indica es que al menos una no es cero.

Razón de varianzas

Esta sección sigue de cerca el texto de Campbell et al. (1997). Siendo r_t el retorno compuesto continuo (diferencia de los logaritmos del precio p_t – p_t– 1) producido durante un período para un activo Z y siendo r_t(2) = r_t + r_t –1, si la serie de los retornos es estacionaria y se divide la varianza de la segunda expresión entre dos veces la varianza de la primera, se tienen una razón de varianzas (VR) dada por:

[5]

En otras palabras, la razón de varianzas de los retornos de un período sobre los retornos acumulados de dos períodos ρ(1) es 1 más el coeficiente de autocorrelación de primer orden. Para el caso de los RW esta razón es 1 ya que todos los coeficientes de autocorrelación son iguales a cero.

La generalización de la expresión para retornos acumulados en q períodos está dada por:

[6]

Si se cumple la hipótesis de RW3 la expresión será uno sin importar el número de retornos acumulados que se tomen.

Bajo la hipótesis nula dada por H o:

Con 2n+1 logaritmos de los precios de los títulos (p₀+p₁+,…, p_2n ) se requiere estimar la media µ y la varianza σ² del proceso, lo cual se puede hacer mediante:

[7]

[8]

[9]

En este caso, los dos primeros son los estimadores de media y varianza que maximizan la función de verosimilitud y el tercero aprovecha la naturaleza de los RW seguidos por p_t y bajo la hipótesis de RW3, la media y la varianza de los incrementos en el precio son lineales en el intervalo del incremento, así que σ² puede ser estimada por la ecuación [9].

En teoría asintótica convencional los tres estimadores son fuertemente consistentes, por lo que se puede probar que la razón de estas varianzas se distribuye asintóticamente como:

[10]

Junto con la generalización de este análisis en q periodos acumulados de retornos se comprimirán dos pasos más. Se corregirá el sesgo que tienen los estimadores de verosimilitud en la estimación de la verdadera varianza y se utilizará el mayor número de datos posible sobreponiendo los datos, como si se tratase de una ventana móvil. Se tendrá entonces que:

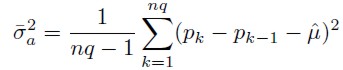[11]

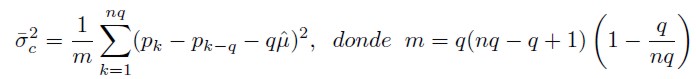[12]

Con la siguiente razón de varianzas generalizada:

[13]

Se tendrá entonces:

[14]

El estadístico (q) permite determinar cuándo la razón de varianzas es estadísticamente igual a 1. Por ejemplo, con un nivel de confianza del 95 por ciento, si el estadístico cae por fuera del intervalo [–1, 96; 1, 96] la hipótesis de caminata aleatoria podrá ser rechazada con un 5 por ciento de significancia.

El estadístico no es robusto ante la heteroscedasticidad y puede llevar a que se rechacen hipótesis nulas de RW3 debido a que la varianza cambia en el tiempo.

Lo y Mackinlay (1988) definen una nueva hipótesis nula compuesta H*-_o con 4 condiciones:

• 
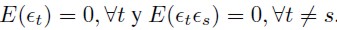
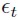• es una perturbación ø-combinada con coeficientes Φ(m) de tamaño 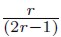o es α-combinada con coeficientes α(m) de tamaño 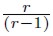, donde, para todo t y para todo τ≥ 0 existe algún δ > 0 para el cual .
• 
• 

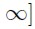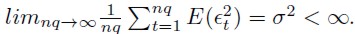
Las definiciones de ø-combinada y α-combinada se presentan en White (1984). Lo que esta hipótesis nula compuesta expresa se resume en que, por una parte, especifica la ausencia de correlación que interesa probar en los RW3 (primera condición) y por otra, deja cierto margen de maniobra para introducir algún tipo de variabilidad en el tiempo de la varianza (condiciones 2 y 3). La condición 4 implica que los coeficientes de autocorrelación en la muestra están asintóticamente no correlacionados (Campbell et al., 1997).

Bajo H*o , el estadístico 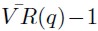converge fuertemente⁶ a 0 para todo incremento no acotado q y n.

El siguiente es un estimador heterocesdásticamente robusto y consistente de :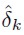

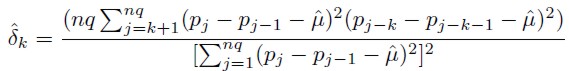[15]

Siendo 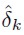la varianza asintótica de los coeficientes de autocorrelación muestrales .

El siguiente es un estimador heterocesdásticamente robusto y consistente de :

[16]

Siendo la varianza asintótica de la razón de varianzas insesgada definida en la ecuación (13).

De lo anterior se puede concluir que ^*(q) es un estadístico de prueba que involucra el hecho de que puede presentarse cualquier forma generalizada de heteroce dasticidad:

[17]

Este es el estadístico de razón de varianzas empleado habitualmente en la literatura contemporánea para poner a prueba la HME en su versión débil, suponiendo normalidad en la distribución de los retornos. El uso que se hace del estadístico tiene al menos dos fallas. La primera es que se calcula estáticamente, es decir, uno para cada mercado. Este método excluye la posibilidad de que un mismo mercado sea eficiente o ineficiente condicional al período y al tipo de situación en la cual se encuentre la economía: en épocas alcistas, bajistas, de burbuja, entre otros. La segunda es que sólo produce una estimación confiable cuando los retornos son normales.

Las series de tiempo financieras exhiben características muy conocidas (ver nota al pie 11) que hacen que el supuesto de normalidad condicional sea imposible de sostener en la estimación. En la siguiente sección se propone una alternativa para el cálculo empírico de la eficiencia.

Cópulas de independencia: una alternativa empírica para la medición de la eficiencia

El problema de la razón de varianzas, como herramientas empírica para la medición de la eficiencia, es que a pesar de incorporar explícitamente un ajuste por heteroscedasticidad, sigue haciendo énfasis en la estimación de relaciones lineales en la historia de la serie. No obstante, la HME en su acepción teórica, no dice nada sobre una relación lineal entre el pasado y el presente de la serie: plantea en general la imposibilidad de dependencia en la serie, tanto lineal como no lineal.

Vale la pena aclarar que una relación de dependencia en la varianza como la supuesta por los modelos de Heteroscedasticidad Condicional Autorregresiva (ARCH)⁷ no invalida la HME, pero sí lo haría cualquier relación no lineal que opere sobre la media de la serie. Ambos puntos se consideran dentro de la medida propuesta en esta sección.

Una alternativa para la contrastación empírica de la eficiencia es el uso de las cópulas, como forma más general para el cálculo de dependencias. éstas se definen en una escala cuantílica y no están atadas en términos generales al supuesto de normalidad subyacente a las correlaciones de Pearson. Formalmente, una cópula es una función de distribución multivariada tal que:

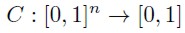[18]

Siendo n las series bajo estudio y C la cópula. En la ecuación (18) se expresa el mapeo desde el hipercubo unitario n dimensional al intervalo unitario, de forma tal que se cumple el teorema de Sklar (1959).

Teorema de Sklar (1959). Sea F una función de distribución multivariada con marginales F₁, …, F_n (no necesariamente continua). Entonces, existe una cópula C : [0, 1]ⁿ → [0, 1], tal que, para todo x₁, … , x_n en R = [– ∞; ∞],

[19]

Si las marginales son continuas, entonces C es única; en otro caso C está únicamente determinada por el Rango (F₁) × Rango (F₂)× … × Rango(F_n), donde, Rango (F_i) = F_i(). Conversamente, si C es una cópula y F₁,… , F_n son funciones de distribución univariadas, entonces la función F definida en la ecuación (19) es una función de distribución multivariada con marginales F₁, … , F_n.

Para una explicación más completa ver Becerra y Melo (2008) o McNeil, Frey y Embrechts (2005). Note que si la variable aleatoria X_i tiene una función de distribución F_i continúa, entonces se tiene que:

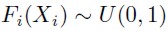[20]

De la misma forma, si U ∼ U(0, 1) entonces F_i –1( U ) ∼ F_i, donde F_i –1 es la función de distribución inversa de F_i, definida como:

[21]

De la ecuación (20) se tiene que:

[22]

Obteniéndose:

[23]

La expresión anterior implica que la cópula puede ser representada en términos de la función de distribución multivariada F y sus distribuciones marginales F₁, … ,F_n. Por otro lado, partiendo de F, F₁,…, F_n y u_i = F(x_i) para i = 1, 2,… n, se tiene que:

[24]

En este estudio las funciones de distribución marginales pueden ser entendidas como las funciones de los retornos de las series financieras en diferentes momentos o con diferentes rezagos. La cópula no impone un número de restricciones en la dimensión de la estimación, lo cual permite que se constituya como una medida más general de la dependencia que las razones de varianza.

Para el caso de las cópulas de independencia, se supondrá que existen dos variables aleatorias x₁ y x₂ y que ambas son independientes, por lo tanto, su función de distribución conjunta es igual a:

[25]

En el caso de independencia la función de distribución conjunta es igual al producto de las funciones de distribución marginales y gracias a las definiciones presentadas en la ecuación (24) se obtiene que:

[26]

En forma general para el caso de n dimensiones la cópula de independencia estará dada por (Becerra y Melo, 2008):

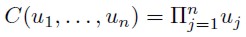[27]

Método de estimación de las cópulas de independencia

En este documento se hace uso de la prueba planteada por Genest y Rémillard (2004), la cual consiste, básicamente, en comparar los cuantiles de la cópula empírica que describen los datos con los de una cópula de independencia simulada, a través de un estadístico propuesto por los autores. Si la evidencia lleva a no rechazar la hipótesis nula de independencia entre las funciones de distribución marginales (en este caso la serie y sus rezagos), la eficiencia estará garantizada, al menos en el sentido de la hipótesis RW2.

Vale la pena mencionar que, tal y como se puede observar en la ecuación (24), la cópula no está definida sobre las series de estudio directamente, sino sobre una seu- do muestra: (u₁,… , u_n) con u_i = F(x_i). El proceso de construcción de la seudo muestra propuesto por McNeil et al. (2005) y Carmona (2004) consiste en utilizar un método semiparamétrico para aproximar la función de distribución. La parte central de las distribuciones se aproximan empíricamente y las colas mediante la utilización de la Teoría del Valor Extremo (TVE). Este m étodo permite construir distribuciones de probabilidad con mayor ajuste para las series financieras⁸.

Un ajuste adicional sobre la serie, necesario antes de estimar la cópula, es la modelación de la varianza, ya que la seudo muestra se construye a partir de la serie estandarizada y no sobre la serie original. Este proceso elimina la dependencia en segundo momento, característica de las series financieras, la cual como se mencionó antes, no interfiere con la HME. La estimación de la varianza condicional se hace mediante modelos GARCH⁹ (1,1).

El procedimiento anterior es empíricamente contrastable mediante el estadístico de prueba de Kolmogorov Smirnoff (KS). En este trabajo se calculó el estadístico KS para la serie de la seudo muestra de cada mercado y en ningún caso se puede rechazar la hipótesis nula de uniformidad (0, 1). También se recurrió a la inspección gráfica de los histogramas de la seudo muestra y a una gráfica cuantil-cuantilentre una distribución uniforme (0, 1) simulada y la muestra construida bajo el procedimiento anterior.

Ninguna de las pruebas permite rechazar la hipótesis nula de ajuste del modelo semiparámetrico estimado para las series bajo estudio. El trabajo de Becerra y Melo (2008) encuentra un ajuste similar para las series colombianas, también con un enfoque semiparámétrico y un modelo GARCH(1, 1) para la estandarización.

RESULTADOS

En este estudio se trabajó con los datos de índices bursátiles de diez países, buscando contrastar los mercados latinoamericanos con los del resto del mundo e intentando plantear la eficiencia en términos relativos, de acuerdo con Campbell et al. (1997). Los índices bursátiles utilizados fueron: IGBC (Colombia), IPC (México), IBOVESPA (Brasil), MERVAL (Argentina), S&P500 (Estados Unidos), FTSE (Inglaterra), SSMI (Suiza), NIKKEI 225 (Japón), HSI (Hong Kong), BSESN (India)¹⁰.

Se construyeron estadísticos de razones de varianza heterocedásticamente robustos como los planteados en la ecuación (17 ) para cada mercado desde julio de 2001 hasta agosto de 2010. Estas razones de varianza se construyeron para todo el periodo muestral y para diferentes momentos, con una ventana móvil de 1.000 datos (aproximadamente 4 años de transacción).

La medida estándar en la literatura es la razón de varianza para todo el periodo de análisis, que capta básicamente las relaciones lineales de dependencia. Esta medida estándar se refina aquí con el cálculo de razones de varianza con una ventana móvil, con las cuales se pretende observar mejor la dinámica en los mercados. Igualmente, se construyeron razones con diferentes rezagos, desde un día hasta treinta días, para cada país en cada momento de tiempo. Esta información se reporta en las Gráficas 1A y 2 A de los anexos, junto con los valores críticos del estadístico.

Las gráficas discriminan entre tres tipos de mercados: los que se comportan eficientemente durante todo el periodo muestral; aquellos que lo hacen parcialmente, durante la mayor parte; y los que se comportan ineficientemente mayoritariamente.

Los mercados más eficientes, en el sentido débil, durante el período de estudio son Japón (NIKKEI 225) y Argentina (MERVAL). La descripción de los estadísticos responde a lo que cabría esperarse bajo la HEM. El estadístico nunca sobrepasa las bandas de confianza al 95 y 99 por ciento.

Los mercados eficientes parcialmente presentan un estadístico que se mantiene predominantemente entre las bandas de confianza al 95 y 99 por ciento. Estos mercados son Brasil (IBOVESPA), Hong Kong (HSI), India (BSESN) y Suiza (SSMI), como se puede observar en la Gráfica 1 A.

Los mercados menos eficientes son los mercados de Colombia (IGBC), Estados Unidos (S&P500), Inglaterra (FTSE) y México (IPC). En estos mercados el estadístico asociado se sale recurrentemente de las bandas de confianza al 95 y 99 por ciento, sobre todo al 95 por ciento. Por ejemplo, el mercado estadounidense es ineficiente desde finales de junio de 2006 hasta octubre de 2008 en mayor medida, pero continúa siéndolo a mediados de agosto de 2010 (al 99 por ciento de confianza). Lo anterior está asociado con la fase final de la burbuja inmobiliaria de ese país, la cual también afectó las cotizaciones bursátiles de las empresas que transan en bolsa, particularmente de las firmas financieras.

El anterior análisis también se puede aplicar al mercado de capitales inglés, en el cual el período de ineficiencia va desde inicios de junio de 2006 hasta finales de septiembre de 2008. La diferencia radica en que a partir de esa fecha el mercado inglés se estaría comportando eficientemente, lo cual no sucede en los Estados Unidos. Lo anterior podría dar indicios de una sobre reacción superior por parte de los agentes en el mercado americano en relación con el inglés. La caída de la bolsa estadounidense al momento de desinflarse la burbuja financiera, al ser aún más acentuada que la de la bolsa en Inglaterra, implicó una mayor correlación serial, que se tradujo en valores más grandes de los estadísticos de las razones de varianza.

En el caso colombiano, el mercado es ineficiente, según la razón de varianzas dinámica, desde el comienzo del periodo de análisis hasta finales de 2009 al 95 por ciento, y finales de 2008 al 99 por ciento.

Los resultados aquí descritos se corroboran con el estadístico de la razón de varianzas para cada mercado, con diferentes rezagos. Con este estadístico se logra captar cuantos días tarda un mercado para ajustar la información, de acuerdo con la HME. En la Gráfica 2A se presenta este estadístico para algunos mercados, en las fechas en las cuales se estimó con mayor valor absoluto (período de mayor ineficiencia).

En la Gráfica 2A se observa que dentro de los mercados menos eficientes, el tiempo que tarda en incorporarse la información en el precio difiere. Mientras que en el caso de Estados Unidos e Inglaterra ésta se tiende a incorporar más rápidamente, en el caso colombiano no termina de reflejarse en el precio ni siquiera después de mes y medio de transacciones, al 99 por ciento de confianza.

Medidas similares se estimaron para todos los mercados, en cada día. Las gráficas no se presentan¹¹, pero en general lo que se observa es que en los mercados más profundos en épocas de ineficiencia la información se incorpora más rápidamente que en los menos desarrollados.

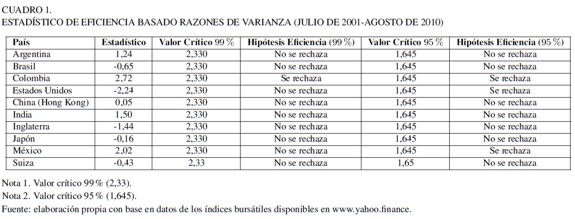
Al estimar las razones de varianza, ya no para una ventana móvil de cuatro años sino para la muestra total, se obtiene el estadístico estándar en la literatura de la razón de varianzas. Los resultados de él se presentan en los Cuadros 1 y 2 junto con los resultados obtenidos con las cópulas de independencia. Como ya se explicó metodológicamente, la estimación de cópulas de independencia corresponde a una prueba de la HME más general, puesto que identifica tanto relaciones lineales como no lineales entre los retornos de los índices bursátiles. Así pues, no se debe encontrar que un mercado sea ineficiente según una razón de varianzas y que sea eficiente con una comparación de cópulas.

En el Cuadro 1 se muestra que Colombia, según la razón de varianzas para toda la muestra, es el único mercado ineficiente al 99 por ciento de confianza. Si se refina el intervalo de confianza hasta el 95 por ciento, pasan a ser ineficientes también los mercados de Estados Unidos y México.

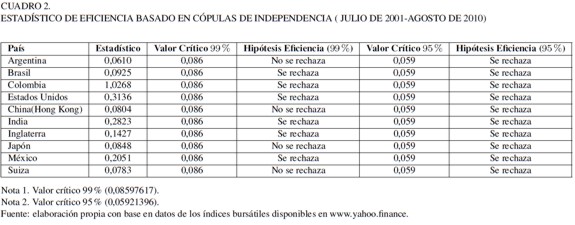
Al analizar los resultados de las cópulas, como una medida más refinada de la eficiencia, ningún mercado es eficiente al 95 por ciento de confianza (Cuadro 2); es decir, en ellos se presentan relaciones de dependencia entre los retornos de la índices bursátiles lineales y no lineales. Al relajar el intervalo de confianza al 99 por ciento, son eficientes los mercados de Japón, Argentina, Suiza y Hong Kong – como era de esperarse por lo encontrado con las razones de varianza. Estos últimos dos mercados tuvieron lapsos cortos de ineficiencia que se observan en las razones de varianza, pero son mercados que predominantemente ajustan sus precios y no sobre reaccionan, mostrando así comportamientos acordes con la HME.

Finalmente, en la Gráfica 3A se presentan los índices bursátiles y las razones de varianza de tres de los mercados menos eficientes (Estados Unidos, Inglaterra y Colombia). Se observa que los períodos de mayor ineficiencia están asociados con burbujas; principalmente con las fases de mayor ascenso en los precios, por encima de sus fundamentales antes del estallido de la burbuja y con el período de ajuste posterior. En el caso de Estados Unidos e Inglaterra lo que se presenta son los momentos cúspide de la burbuja residencial y financiera que comenzó en los años noventa y estalló entre 2007 y 2009. En Colombia, el ascenso del IGBC antes de 2006 estuvo asociado con una sobrevaloración de los activos internos, producto de un exceso de liquidez en el mercado (Uribe, 2007), que fue corregido para esta fecha por parte de las autoridades monetarias, mediante incrementos sucesivos en la tasa de interés de referencia.

CONCLUSIONES

Las conclusiones de esta investigación apuntan en dos direcciones. Primero, le revisión de la literatura indica un claro nexo entre eficiencia informacional y eficiencia en el sentido de Pareto, luego es importante estudiar la eficiencia informacional; con este marco teórico en mente se procede a las conclusiones empíricas.

Del análisis del trabajo de Rostchild y Stiglitz (1976) y Stiglitz (1981) se puede ver que la eficiencia en el sentido de Fama (1970), también conocida como eficiencia en la información, puede ser entendida como una condición necesaria más no suficiente para que los mercados financieros sean eficientes en el sentido de Pareto. Cualquier recomendación de política económica deberá tener en cuenta esta relación.

A pesar de las limitaciones teóricas del concepto de eficiencia, sobretodo en el sentido fuerte y que fueron señaladas claramente en Grossman y Stiglitz (1980), ésta sigue constituyendo una propiedad deseable de los mercados financieros, toda vez que es una condición necesaria para garantizar que se cumpla el Primer Teorema del Bienestar. De lo anterior se desprende la necesidad de revaluar las posiciones que pretenden desligar los conceptos de eficiencia informacional y en la asignación (Hyme, 2003).

Las aproximaciones metodológicas estándar para medir la eficiencia en el sentido débil, básicamente a través de razones de varianza y estadísticos de correlación serial, presentan dos debilidades:

1. Son medidas estáticas que no tienen en cuenta que un mismo mercado en distintos momentos puede pasar de ser eficiente a ser ineficiente, o lo contrario, dependiendo por ejemplo de la aparición de burbujas especulativas en su interior¹².

2. Sólo miden dependencias lineales en los niveles de los retornos, es decir, contrastan una caminata aleatoria de tipo 3 (RW3) en la tipología de Campbell et al. (1997), lo cual es mucho más restrictivo que el concepto teórico de eficiencia, que nunca impone los conceptos de linealidad y de normalidad.

Lo primero se puede solucionar con el cálculo de razones de varianza heterocedásticamente robustas en forma dinámica, a través de ventanas móviles, como se hace en este documento y lo segundo, mediante la estimación del estadístico de independencia propuesto por Genest y Rémillard (2004), basado en las cópulas empíricas de los datos y una cópula de independencia simulada.

Al aplicar estas mejoras en la estimación para los datos de diez mercados financieros en el mundo (Colombia, México, Argentina, Brasil, Estados Unidos, Inglaterra, Suiza, India, Hong Kong y Japón), se encuentra que difícilmente la HME se mantiene durante el periodo analizado (enero de 2001 a agosto de 2010).

Al 99% de confianza sólo cinco mercados resultan eficientes, en tanto que al 95% no lo es ninguno, según la medida basada en cópulas.

El resultado se captura mejor mediante el uso de razones de varianza dinámicas y cópulas, que mediante las razones estáticas o los coeficientes de autocorrelación. Según los hallazgos de este trabajo, los mercados que tienden a sobre reaccionar ante los choques y que por ende son propensos a crear burbujas, se comportan de forma menos eficiente que aquellos que no. De la misma forma, existen mayores indicios de ineficiencia informacional en los períodos expuestos a grandes choques que en aquellos de relativa calma. Investigaciones más profundas deberán hacerse sobre la relación teórica y empírica entre burbujas en el precio de los activos e ineficiencia.

ANEXOS

NOTAS AL PIE

1 Sobre este patrón recurrente véase Marichal (2010). En particular señala, refiriéndose a las crisis del 29 y subprime: “A su vez, en ambos casos las crisis fueron precedidas por un extraordinario auge bursátil, inflado a raíz de un notable incremento de la oferta de crédito por parte de firmas de inversión que desembocó en una serie de burbujas financieras” (Marichal, 2010, 317).

2 Fama (1990) modifica, posteriormente, el postulado general de la HME como consecuencia de este señalamiento.

3 A saber: u ⁱ es continua, estrictamente creciente y estrictamente cuasicóncava en 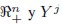satisface que 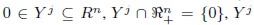es cerrado y acotado y Y j es estrictamente convexa.

4 En el caso estudiado por los autores, que es el mercado de seguros, se permite que quienes contratan el seguro conozcan más sobre su propio comportamiento y su propensión a tener accidentes que las empresas aseguradoras.

5 Dicho de otra forma, si no hay eficiencia en la información, ya que los precios no recogen la información disponible porque la información es asimétrica, no se cumple el primer teorema del bienestar, que establece que todas las asignaciones del EGW serán Pareto-Eficientes.

6 Almost sure convergence.

7 Este modelo fue originalmente planteado en Engle (1982) y su generalización más popular se encuentra en Bollerslev (1986).

8 Las series financieras tienen características muy reconocidas: al ser heterocedásticas, leptocúrticas y asimétricas (Christoffersen, 2003).

9 Generalized Autoregressive Conditional Heteroscedasticity.

10 Se analizó también el mercado de Chile, pero no se presentan los resultados puesto que la información disponible sólo comprende desde septiembre de 2003 y el período de estudio comienza antes, en julio de 2001.

11 Pueden ser solicitadas a los autores, a través de correo electrónico.

12 La relación entre burbujas y eficiencia en el mercado requiere de un mayor estudio al que se presenta en este trabajo. Futuras investigaciones podrán apuntar en esta dirección.

REFERENCIAS BIBLIOGRÁFICAS

[1] Arrow, K.J. y Debreu, G. (1954). Existence of an Equilibrium for a Competitive Economy. Econometrica, 22(3), 265-290.        [ Links ]

[2] Bachelier, L. (1900). Théorie de la Spéculation. Annales Scientifiques de L'é.N.S.,3(17), 21-86.        [ Links ]

[3] Becerra, O. y Melo. L.F. (2008). Usos e Implicaciones de la Cópula en la Medición del Riesgo Financiero (Borradores de Economía, 489). Bogotá: Banco de la República. Recuperado de: http://www.banrep.gov.co/publicaciones/pub_borra.htm        [ Links ]

[4] Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31(3), 307-327.        [ Links ]

[5] Box, G.E.P. y Pierce D. (1970). Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. Journal of the American Statistical Association, 65(332), 1509-1526.        [ Links ]

[6] Campbell, J., Lo, A.W. y MacKinlay, A.C. (1997). The Econometrics of Financial Markets. New Jersey: Princeton University Press.        [ Links ]

[7] Carmona, R. (2004). Statistical Analysis of Financial Data in S-Plus. Nueva York: Springer-Verlag.        [ Links ]

[8] Christoffersen, P. F. (2003). Elements of Financial Risk Management. California: Elsevier.        [ Links ]

[9] Engle, R.E. (1982). Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation. Econometrica, 50(4), 987-1008.        [ Links ]

[10] Fama, E.F. (1970). Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance, 25(2), 383-417.        [ Links ]

[11] Fama, E.F. (1991). Efficient Capital Markets: II. The Journal of Finance, 46(5), 1575-1617.        [ Links ]

[12] Fama, E.F. (1998). Market Efficiency, Long Term Returns, and Behavioral Finance. Journal of Financial Economics, 49(1), 283-306.        [ Links ]

[13] Fama, E.F. y French, K.R. (2010). Luck versus Skill in the Cross Section of Mutual Fund Returns. The Journal of Finance, 65(5), 1915-1947.        [ Links ]

[14] Genest, C. y Rémillard. B. (2004). Test of Independence and Randomness Based on the Empirical Copula Process. Test, 13(2), 335-369.        [ Links ]

[15] Grossman, S. y Stiglitz, J. (1980). On the Impossibility of Informationally Efficient Markets. The American Economic Review, 70(3), 393-408.        [ Links ]

[16] Hyme, P. (2003). La Teoría de los Mercados Eficientes. Un Examen Crítico. Cuadernos de Economía, 22(39), 57-83.        [ Links ]

[17] Jehle, G. y Reny, P.J. (2001). Advanced Microeconomic Theory. Massachusetts: Addison Wesley.        [ Links ]

[18] Kendall, M.G. (1953). The Analysis of Economics Time Series, Part I: Prices. Journal of the Royal Statistical Society, 116(1), 11-34.        [ Links ]

[19] Ljung, G.M. y Box, G.E.P. (1978). On a Measure of Lack of Fit in Time Series Models. Biometrika, 65(2), 297-303.        [ Links ]

[20] Lo, A. y Mackinlay, A.C. (1988). Stocks Markets Prices Do Not Follows Random Walks: Evidence for a Simple Specification Test. The Reviews of Finance Studies, 1(1), 41-66.        [ Links ]

[21] Malkiel, B.G. (1987). Efficient Market Hypothesis. En Eatwell, J., Milgate, M. y Newman, P. (eds.). New Palgrave: A Dictionary of Economics 2 (pp. 120-123). Hampshire: Macmillan.        [ Links ]

[22] Malkiel, B.G. (1999). A Random Walk Down Wall Street: The Best Investment Advice for the New Century Completely Revised and Updated. New York: W.W. Norton & Company.        [ Links ]

[23] Malkiel, B.G. (2003). The Efficient Market Hypothesis and Its Critics. Journal of Economic Perspectives, 17(1), 59-82.        [ Links ]

[24] Malkiel, B.G. (2005). Reflections on the Efficient Market Hypothesis: 30 Years Later. Financial Review, 40(1), 1-9.        [ Links ]

[25] Mandelbrot, B. (1966). Forecast of Future Prices, Unbiased Markets, and Martingale Models. Journal of Bussines, 39(1,2), 242-255.        [ Links ]

[26] Mandelbrot, B y Hudson, R. L. (2006). The (Mis)behavior of Markets. New York: Basic Books.        [ Links ]

[27] Marichal, C. (2010). Nueva Historia de las Grandes Crisis Financieras. Una Perspectiva Global 1873-2008. Ciudad de México: Debate.        [ Links ]

[28] McNeil, A.J., Frey, R. y Embrechts, P. (2005). Quantitative Risk Management: Concepts, Techniques, and Tools. New Jersey: Princeton University Press.        [ Links ]

[29] Peters, E. (1996). Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility. New York: John Wiley & Sons.        [ Links ]

[30] Roberts, H. (1967). Statistical Versus Clinical Prediction of the Stocks Markets (manuscrito no publicado). Chicago: Center for Research in Security Prices, Universidad de Chicago.        [ Links ]

[31] Rothschild, M. y Stiglitz, J. (1976). Equilibrium in a Competitive Insurance Market: An Essay on the Economics of Imperfect Information. The Quaterly Journal of Economics, 90(4), 629-649.        [ Links ]

[32] Samuleson, P. (1965). Proof that Properly Anticipated Prices Fluctuate Randomly. Industrial Management Review, 6(2), 41-49.        [ Links ]

[33] Sklar, A. (1959). Fonctions de Repartition á n Dimensions et Leurs Marges. Publi cations de l'Institut de Statistique de l'Université de Paris, 8, 229-231.        [ Links ]

[34] Stiglitz, J. (1981). The Allocation Role of the Stock Market. Pareto Optimality and Competition. The Journal of Finance, 36(2), 235-251.        [ Links ]

[35] Stiglitz, J. (2010). Freefall: America, Free Markets, and the Sinking of the World Economy. New York: Norton & Company.        [ Links ]

[36] Uribe, J.M. (2007). Caracterización del Mercado Accionario Colombiano 2001- 2006: un Análisis Comparativo (Borradores de Economía, 456). Bogotá: Banco de la República. Recuperado de: http://www.banrep.gov.co/publicaciones/pub_borra.htm        [ Links ]

[37] Von Neumann, J. y Morgenstern, O. (1944). Theory of Games and Economic Behavior. New Jersey : Princeton University Press.         [ Links ]

[38] White, H. (1984). Asymptotic Theory for Econometricians. Orlando FL: Academic Press.        [ Links ]

[39] Working, H. (1934). A Random Difference Series for Use in the Analysis of Time Series. Journal of the American Statistical Association, 29(185), 11-24.        [ Links ]