INTRODUCTION
Education plays a dual role in the process of intergenerational transmission of socioeconomic status. It can be one of the main channels of social mobility, while at the same time it can also lead to the reproduction of inequalities. The scope of education to promote mobility depends on the effect that the family environment of origin has on children’s educational achievement (Torche, 2010). In particular, it depends on the effect of parental education on children education, that is, on the intergenerational educational mobility (IEM) that exists in a society.
The analysis of education transmission between generations is a starting point to better understand the key factors explaining intergenerational relationships in other relevant variables such as income. Indeed, educational attainment is a good proxy of an individual’s human capital endowment that, in turn, is positively correlated with permanent income (Checchi, Fiorio, & Leonardi, 2008)1. In addition, there is a close relationship between IEM and intergenerational income mobility. In a recent study, Blanden (2013) formally derived relations between the two most commonly used indicators to measure intergenerational persistence of education and income: the correlation coefficient educational and intergenerational elasticity of income. From the empirical point of view, there is evidence showing the relationship between decreases in intergenerational income mobility and increases in educational persistence across generations (Blanden, Gregg, & Macmillan, 2007).
Although the literature on transmission of education between parents and children has grown, most existing research exams IEM at a given point of time. Studies that attempt to measure intergenerational mobility (IM) from a time perspective are less numerous. However, this analysis can lead to a deeper understanding of the mechanisms underlying the intergenerational transmission of income (Aaronson & Mazumder, 2008). In addition, the dynamic analysis of IM allows us to investigate whether high or low immobility between generations observed in a given country is a relatively recent phenomenon or a temporarily persistent feature.
Therefore, the first objective of this article is to examine the IEM level and its evolution in Latin America from a novel data base obtained from a public opinion survey called “Latinobarómetro” held annually in several countries in Latin America. The main advantage of this survey is the availability of retrospective information on parental education for all adults surveyed. Given the absence of adequate data to analyse trends in intergenerational income mobility in Latin America, it is considered that education provides an appropriate socioeconomic variable to examine the evolution of intergenerational social mobility between birth cohorts.
Moreover, the concept of mobility is still in development, and as a result, there is less consensus on how to measure mobility in relation to the measurement of inequality (Benabou & Ok, 2001 and Formby, Smith & Zheng, 2004). More important is the lack of consensus on how to evaluate the processes of mobility in the not so numerous studies that explicitly discussed this important issue. Following Benabou and Ok (2001), this research considers that equal opportunity2 (EOP, for short) provides a very natural approach to evaluate the process of intergenerational mobility. In this context, the importance of social mobility between generations is not that the movements between parents’ and children’s socioeconomic positions are intrinsically valuable, but it is expected to help reduce the negative effects of disparities in endowments on future outcome (Stokey, 1998).
There are many reasons for analysing the relationship between the IM and the EOP concepts. The degree of equal economic and social opportunity establishes to what extent the circumstances of a person’s childhood affect their future outcome or, conversely, indicates the extent to which individuals can obtain a certain result thanks to his own talent, motivation and effort (Blanden, Gregg & Machin, 2005). Thus, intergenerational mobility can have important consequences for economic efficiency (Conconi, Cruces, Olivieri, & Sánchez, 2008). Greater IM, insofar as it implies the existence of more equal opportunity, promotes a more efficient allocation of the skills and potential of individuals because it allows for a more optimal allocation of individuals based on their abilities in activities which are consistent with its comparative advantages. Moreover, the perceived economic inequality and inequality of opportunity is probably one of the main sources of discontent and social and political instability. This is related to the so-called tunnel effect, Hirschman and Rothschild (1973), to which reference is made in the Introduction and illustrates the tolerance of inequality in different contexts of mobility.
However, in general, IM measures are related to the notion of EOP but do not correspond directly to it. In particular, income movements between generations can be equalizing or unequal and the mobility indicators proposed in the literature fail to distinguish them.
Therefore, another objective of this research is to implement a suitable method that allows us to determine the implications of the observed levels of intergenerational mobility for the existence of equal opportunity, as well as to measure the degree to which the intergenerational mobility produces a levelling effect of opportunities. It is also intended to analyse the most appropriate way of comparing intergenerational mobility processes in order to implement a robust criterion for their ordering. For this, a new technique, recently proposed by Anderson, Leo and Muelhaupt (2014), is used to measure the degree of overlap between the conditional density of the education of the children given the parents’ education and the theoretical density corresponding to a situation of EOP or independence bet-ween the two variables. One of the main advantages of this method over other existing ones (such as the stochastic dominance approach formulated by Lefranc, Pistolesi, & Trannoy, 2008, 2009) is that it offers a measure (called overlap index) that indicates the degree of progress toward equal opportunity offered by a society as a whole or by a particular socioeconomic group. This is particularly useful as a statistic for making temporary comparisons of observed mobility processes or for evaluating, for example, which socioeconomic group benefited most from a policy that seeks to equalize opportunities.
Research on IEM in Latin America, as well as on intergenerational mobility in general3, faces as a main difficulty the lack or the limitations of information on parents’ and children’ socioeconomic characteristics for adult individuals. In this context, studies were developed by Behrman, Birdsall and Szekely (1999), Dahan and Gaviria (2001) and Andersen (2001) who propose intergenerational mobility indexes4 that can be computed from the information generally available in the household surveys conducted in the different regions of the countries. These indexes were used in several IEM studies. Other more recent IEM studies in Latin America5 are those undertaken by Conconi et al. (2008), Torche (2010), Mediavilla and Calero (2010) and Daude and Robano (2015). In their empirical study, Conconi et al. (2008)compute the previously mentioned mobility indexes of Behrman et al. (1999), Andersen (2001) and Dahan and Gaviria (2001) for Latin American countries in the early 1990s and 2000s. The results indicate that, during the period considered, mobility in Latin America increased, although not in the same magnitude in all countries. For their part, Mediavilla and Calero (2010) calculate and compare the degree of IEM in six countries of the region using data from house-hold surveys for 1998-1999. The study by Torche (2010)6 for four countries in the region aims to analyse the effect of the macroeconomic context on the evolution of the IEM and finds a negative effect of the economic crises on the IEM. In a recent article, Daude and Robano (2015) examine IEM levels in 18 Latin American countries based on the Latinobarómetro public opinion survey of 2008. This is one of the few studies that empirically analyse the relationships between an indicator of IEM and an index that measures unequal opportunity7.
In conclusion, several of the existing IEM studies in Latin America estimate indexes from household surveys for adolescents and young people living with their parents. Also, some of these indexes, such as those proposed by Behrman et al. (1999), Andersen (2001) and Dahan and Gaviria (2001) do not measure IEM directly, but constitute an indirect approach. This indirect approach is based on measuring the importance of the family environment as a determinant of children’s and young people’s educational outcomes. Specifically, it is assumed that the more important the origin of socioeconomic characteristics as determinants of access to educational opportunities for young people, the greater the persistence of these characteristics and the smaller the mobility. In contrast, this article uses a novel database containing information about children’s and their parents’ education for all adult individuals interviewed, regardless of whether or not they live with their parents. This allows a direct approach to measure and characterize IEM. On the other hand, most of the studies mentioned do not formally examine the relation-ships between the observed IEM and the equal opportunity concept8. Likewise, to evaluate the processes of intergenerational mobility observed from the equal opportunity approach, a new technique recently proposed by Anderson et al. (2014) is implemented here for the first time in another country. The latter constitutes one of the main contributions of the present study to the existing literature.
INTERGENERATIONAL MOBILITY AND EQUAL OPPORTUNITY
From a normative perspective, there is a growing consensus in favour of equal opportunity, a characteristic generally more desirable for society than equality of outcome as the relevant objective to guide public policies. However, it should be noted that this prioritization of social policies has been questioned, among others, by Dubet (2011) who, after analysing these two models of social justice, equality of outcome, or positions and equality of opportunity, defends the first over the second, making it clear that such a choice does not mean that equal opportunity should be ignored, but that it establishes a priority, considering that public action consists of ranking the objectives. Dubet’s general critique of the concept of equal opportunity lies in its relation to the meritocratic principle of social justice. Thus, for the author, this conception of justice consists in offering everyone the possibility of occupying the best positions according to a meritocratic principle, without questioning the gap between positions. In favour of the model of equality of results or positions, the author argues that it is more beneficial to the weaker people given that it indirectly favours equality of opportunity more than this model of justice and because the relative equality between social positions is considered good since inequalities end up affecting society as a whole. Without ignoring Dubet’s proposal, recognizing that this discussion exceeds the limits of the economy and corresponds to the field of philosophy, it is considered that there are several reasons that justify the analysis of the relationship between IM and equal opportunity, beyond the order of priority that corresponds to this last objective in the political agenda.
The investigations that formally analyse, from the theoretical or empirical point of view, the relations between intergenerational mobility and equal opportunity are relatively recent and still quite rare. As Van de Gaer, Schokkaert and Martinez (2001) say, empirical studies often compute indices of intergenerational mobility and then, implicitly or explicitly, and without a clear theoretical basis, the findings are interpreted in the light of normative criteria related to concepts such as equality of opportunity. In relation to this, it should be noted that the vast majority of the empirical literature that proposes to estimate the level of IM, implicitly assumes the existence of equal opportunity when the rows of the intergenerational income matrix are identical or, in general, if the probability that an individual will reach a certain level of income is independent of his parents’ income. However, as Roemer (2004) warns, this criterion implies assuming a particular concept of EOP that, from the social and normative point of view, can be quite strict or “radical” and therefore not totally acceptable. Roemer’s (2004) study, which is one of the few researches that seeks to formally analyse the relationship between equal opportunity and IM, proposes four approaches to defining equality of opportunity based on the inclusion of a set of circumstances considered socially not acceptable9. According to Roemer’s (1998, 2004) vision of “levelling the playing field”, opportunities are actually identical when all individuals who spent the same degree of effort, regardless of their “type”10, have the same chances of achieving the objective. In other words, according to this approach, there is equality of opportunity when individuals who applied the same degree of effort are equally likely to achieve an outcome regardless of their circumstances. Therefore, the concept of EOP is intimately related to the distinction between circumstances and effort. Circumstances are aspects of the environment that affect socioeconomic status that are not under the agent’s responsibility. Effort, on the other hand, is the set of actions that affect the status of an individual and for which he can be held responsible. In this scheme, Roemer (2004) argues that the more strict or “radical” conception of EOP, denoted by the author as EOP4, implies that policy makers should level the playing field by eliminating the influence, not only of social connections, investments and family culture as well as the genetic transmission of skill, but also the influences of the family environment in the formation of preferences and aspirations among children. Thus, the concept of equality of opportunity implies only under quite extreme circumstances (those considered in the EOP4 approach); complete IIM.
In addition, some mechanisms of intergenerational persistence, such as genetic inheritance, would exist even in a society where institutions fully compensate for the social disadvantages of origin. If these mechanisms strongly determine socioeconomic success, then the intergenerational association of outcomes could be high even if there were equal opportunity, in a less strict sense (Jenks & Tach, 2006; Torche, 2015). Therefore, considering that equality of opportunity only exists when there is no association between the income of parents and children can be difficult to accept. Hence, for Roemer (2004), studies on IM should make an effort to test the existence of equal opportunity from less radical points of view.
Another study that examines the relationship between equality of opportunity and income mobility is that of Benabou and Ok (2001). If the mobility process is considered to be a potential equalizer of opportunities, it follows that what should be measured is the degree to which it produces this levelling effect. This, in turn, corresponds, according to Benabou and Ok (2001) with a notion of redistribution of income, although stochastic. Thus, just as a tax scheme maps pre-tax incomes into post-tax incomes, the mobility process maps initial incomes into expected future incomes or, in general, into expected levels of intertemporal welfare. Therefore, the degree to which income mobility is more or less of an equalizer of opportunities can be measured by the degree of progressivity of that mapping, in the sense of having a decreasing average “tax” rate. From this idea, the authors theoretically characterize the mobility processes according to their progressivity or potential of equalization of opportunities and offer a simple criterion to determine if one process is more progressive (equalizer of opportunities) than another. They also demonstrate how this ordering relates to the analysis of social welfare.
A study that adopts a theoretical approach related to that proposed by Benabou and Ok (2001) in the specific context of measuring the degree of intergenerational mobility is that developed by Van de Gaer et al. (2001). These authors propose an “equality of opportunity index” based on the expected income of an individual, conditional on the income class of their parents and the probabilities of reaching each of the income classes considered in the relevant row of the matrix of transition between two generations.
On the other hand, in a recent research, Anderson et al. (2014) review the relationship between IM and the EOP approach by noting the limitations of existing techniques to evaluate the progress of some public policy in terms of EOP. The authors propose a new approach that they call “qualified equal opportunity” (QEO). According to the authors, policy actions aimed at QEO focus on improving the life chances of those who received a “poor heritage” from their parents rather than diminishing the opportunities of those who received a “rich heritage”11. In this way a QEO program emerges with asymmetric mobility goals to increase the mobility of the poorly endowed and not to do it among the richly endowed when this implies a loss of their wellbeing. However, changes in the coefficient of parents’ socioeconomic status in a generational regression or mobility index (as a consequence of changes in the relative magnitudes of the elements of a transition matrix) do not adequately reflect the asymmetric nature of a policy that tends to equalize opportunities in this way. In addition, even the stochastic dominance approach proposed by Lefranc et al. (2008, 2009) that identifies the lack of EOP does not produce a statistic that indicates the degree of change or progress that exists towards EOP. Therefore, it is necessary to rethink the current empirical approach to evaluate the EOP and the logic of a program that aims for QEO. A program such this should not be characterized as movements towards independence of results and circumstances for all groups. On the contrary, a QEO program implies limited movements that modify the joint distribution of results and circum-stances differently towards independence for those who come from a disadvantaged background compared with those who possess advantageous circumstances.
In short, unlike the vast majority of previous empirical studies on intergenerational mobility in general, and those examining its temporal changes in particular, this research explicitly uses the equal opportunity approach to assess the evolution of intergenerational mobility. Specifically, it examines if the observed changes in the IEM process implied an increase in the levels of EOP. Also, based on the QEO approach, this article seeks to determine whether these changes produced improvements or progress in the opportunities faced by those belonging to the most disadvantaged socioeconomic groups. To test this hypothesis and evaluate the intergenerational mobility processes observed in each cohort from the perspective of equal opportunity, the criterion proposed by Anderson et al. (2014) is used.
METHODOLOGY
Transition matrices document the movements of individuals between different classes; specifically, intergenerational transition matrices by educational levels indicate a child’s probability of reaching a certain educational level, conditional on the parents’ educational level. This method allows us to observe, not only whether there is more or less intergenerational mobility in the different parts of the education years distribution, but also the direction of mobility (Jenkins & Siedler, 2007). At the same time, the transition matrices allow us to examine the asymmetries and other nonlinearities in the IEM. However, one of the disadvantages of this method is that it does not offer a unique measure of mobility that facilitates comparisons. And, although from the transition matrices it is possible to obtain indicators that summarize the observed transitions, as Van der Gaer et al. (2001) say, the existing IM indexes do not provide a good measure of the degree of equality of opportunity. Nevertheless, interest in this aspect is always present, implicitly or explicitly, when analysing intergenerational transition matrices.
With the objective of evaluating the extent to which the intergenerational educational mobility processes observed generated changes in the levels of equal educational opportunity, the technique of Anderson et al. (2014) is used. This technique basically consists of measuring how close the observed joint density of the parents’ and children’s results (educational levels, in this case) is to the density that reflects independence (EOP) or conditional independence (QEO) in those results. Hence, the index measures the degree of overlap between the observed joint density and a theoretical density that reflects the hypothesis of interest being tested as the degree of EOP or QOP in this case. This measure is easy to compute and is asymptotically normal when a random sample is used; therefore, statistical inference can be performed. One of the main advantages of this index is its adaptability to consider both discrete and continuous variables and even combinations of both types of variables in multiple dimensions (Anderson et al., 2014). In particular, the overlap (OV) measure for discrete variables (such as the ones considered in this case)12 is as follows:
Where j i,k =Pr(i,k) is a typical element of a joint density which measures the probability of observing a child with a result i given that his parents have the result k, the superscripts O and E of j i,k indicate whether the probability corresponds to the observed joint density and the theoretical density respectively.
This technique is easily adaptable to examine, not only the hypothesis of independence, but any other hypothesis of interest. Anderson et al. (2014) describe the measurement of overlap graphically from the Figure 1 where the distribution f represents the observed density and g corresponds to the theoretical density. The OV index measures the overlap area between the two densities so that this measure will approach 1 the more f y g coincide, and vice versa, it will tend toward 0 the less common surface there is between the two distributions.
To examine the independence hypothesis or EOP, the OV measure takes the following form:
Where h i =Pr(i) is the probability of observing a child with result i and P k =Pr(k) is the probability of observing parents with result k such that, /. Therefore, h i p k is the typical element (i, k) of the theoretical joint density between two independent variables.
In order to evaluate the QOE hypothesis to identify if progress is observed in a particular segment of the population, the OV measure to be considered for each interest group is as follows:
Anderson, Linton, & Whang (2012) discuss the estimation of these measures as well as those of their standard errors. The bootstrap method is used here to compute the standard errors of the OV indexes. An interesting aspect of this technique is its relation to the concept of polarization. In fact, the OV index can also be used in another context as a measure of the degree of polarization between two groups defined by race, occupation, gender, and so on13.
This technique has several advantages over other existing approaches which assess the degree of equal opportunity associated with a given intergenerational mobility process, such as the generational regression model that relates a child’s result as a dependent variable to the parents’ result as an independent variable, the mobility indexes derived from transition matrices, and the recent approach of Lefranc et al. (2008, 2009). Thus, changes in the parent outcome coefficient in an intergenerational regression or changes in mobility indices estimated from parent-child transition matrix do not correctly capture the progress toward EOP of a particular socioeconomic group; that is, the asymmetric nature of the mobility process or the QOE policies (Anderson et al., 2014).
The main difficulty with intergenerational regressions hinges on the notion that zero covariance does not imply independence between the child’s outcome and paternal circumstance. In addition, the linear specification of these regression models implies that the marginal effect of the particular paternal characteristic being analysed (education, for example) is the same across the entire distribution of that variable as well as the dependent variable. One way to reduce these problems is to use the nonparametric quantile regression (QR) technique. However, this approach cannot be implemented in this case given the categorical nature of the variables of interest (educational levels of parents and children). In addition, the QR method does not offer a statistic like the OV index that summarizes in a single number the degree of progress toward equality of opportunity (Anderson & Leo, 2015).
One of the main difficulties of the approach that uses transition matrices and their derived indexes is its implementation when the result variable and the variable of interest are measured in different metrics and discrete and continuous dimensions. Another problem with this approach is that it relies on partitioning the outcome and circumstance space into common segments in order to estimate the transition matrix. An additional problem is that proximity to independence in this context is difficult to evaluate, therefore some function of the matrix components (such as the trace or determinant of the transition matrix) is generally used. Another problem is the potential test inconsistency issue when the difference between two continuous distributions is compared at discrete points of the support, as in this approach. This implies, in practical terms, that an incorrect selection of the partition structure could lead to inferring a magnitude of independence which did not actually exist (Anderson & Leo, 2015).
On the other hand, the stochastic dominance approach, although it allows us to evaluate the existence or lack of EOP, it does not yield a measurement or indicator which indicates the degree of progress toward equality of opportunity, as does the overlap technique through the OV index (Anderson et al., 2014).
DATA
The data used in the empirical analysis comes from a public opinion survey called “Latinobarómetro” conducted annually in Latin America. This survey began in 1995 in 8 countries and has been implemented on a yearly basis thereafter14. However, only since 2003 have the survey samples for all countries been representative of the national population.
The main advantage of this survey for an IEM study in relation to other existing surveys for Latin America is the availability of retrospective information about the education of the parents for all individuals surveyed, regardless of whether they reside or not, at the moment of the interview, in the same home where their parents live15. Although the Latinobarómetro surveys contain an adequate socioeconomic characterization of each individual, they do not include accurate measurements of family income.
In order to examine the temporary changes that took place in the IEM, data from the surveys for the period 2003-2013 and for 201516 are used, for which, as previously indicated, samples with national, urban and rural representativeness are available. In order to examine the temporal trends in IEM during the longer period, the analysis is based on comparisons between birth cohorts. The availability of data from several cross-section surveys allows for a greater number of observations to make estimates by birth cohort with more precision. Likewise, the possibility of following each birth cohort over several years and observing their results at different ages limits the confusion of cohort and age effects that occurs in this type of longitudinal analysis. However, as already mentioned, educational levels generally have little or no life cycle effect after the age at which most individuals stop studying and enter the labour market.
In the empirical analysis, individuals from 25 to 64 years of age are considered. Individuals older than 25 years are included because this is the theoretical age in which formal education is usually concluded. While individuals older than 64 years are not considered in order to avoid possible biases in estimates by including older cohorts (Daouli, Demoussis, & Giannalopoulos, 2010). In addition, the individuals in these birth cohorts have fewer observations compared to the rest. Individuals aged 25 to 64 years in 2003 to 2013 and 2015 belong to the birth cohorts between 1949 and 1988. In order to have greater precision in the estimates, these cohorts were grouped into the following four decades: 1949-1958, 1959-1968, 1969-1978, and 1979-1988.
Despite the smaller sample size of the Latinobarómetro surveys, it should be noted that there are no significant differences in the average years of education obtained from the sample and those resulting from national household surveys (Daude & Robano, 2015)17.
Table 1 presents some descriptive statistics of the education of the children and their parents by birth cohort (which are the main variables of interest) as well as the number of observations available in each case. It should be mentioned that in the Latinobarómetro survey this variable is truncated in the higher educational levels. That is, for those who have incomplete post high school studies their years of education are unknown. In these cases, individuals were counted based on the most frequently observed years of education for those educational levels in other household surveys available for Argentina. However, because this problem can generate a measurement error in the variables, we decided to use the educational level.
RESULTS
This section examines the intergenerational educational mobility processes from the EOP approach, based on the OV index (IOV) recently proposed by Anderson et al. (2014). This measure allows us to evaluate the existence of EOP in each birth cohort considered. According to equation (1), this can be done by comparing each of the observed joint density of parents’ and children’s educational levels with the joint density that would theoretically exist under the assumption of EOP or independence between the educational level of parents and children. The more the observed and theoretical joint density coincide (differ), the more the OV index tends toward 1 (0).
Throughout the analysed period, the observed joint densities and those estimated under the hypothesis of independence between the educational level of parents and children became closer according to the OV indexes computed for the different birth cohorts18. Thus, this measure increased between the oldest and the youngest cohort, 33% for all the children, 28% for men, and 36% in the case of women. This implies an improvement in terms of EOP for younger generations compared to older ones.
However, the overall OV index does not allow us to determine which socioeconomic group benefited from the EOP perspective. This implies evaluating the so called QEO hypothesis which, in general terms, establishes that the conditional density of achievement of the children belonging to the most disadvantaged socioeconomic group should be close to the marginal density of children’s achievement, as compared to the children of groups of greater socioeconomic status.
Table 1 Descriptive Statistics by Sex and Birth Cohort. 2003-2015

Note: C1: cohort 1 (1949—1958). C2: cohort 2 (1959-1968). C3: cohort 3 (1969-1978). C4: cohort 4 (1979-1988). Standard deviations in parentheses. Source: Authors’ compilation based on Latinobarómetro survey 2003-2013.
The OV index of equation (3) allows us to test this hypothesis because it measures the degree of overlap between the two densities for each socioeconomic group defined, in this case, by the paternal educational level. If the parents’ and children’s educational level are independent, then the OV index will present values close to 1, indicating compliance with the EOP hypothesis for that group. To the extent that the children’s educational level depends more on parents’ education, so that the conditional density moves away from the marginal density of the education of the children, the index will register a value substantially less than 1 and close to 0. Therefore, the further away the measure is from 1 for a particular group, the lower the EOP is among the children from the same group. In this way, the OV index allows us to not only to evaluate the existence of equal opportunity but also to determine how far away a particular group is from an EOP situation in which the result obtained by the children does not depend on their parents’ characteristics. This measure also facilitates comparisons of the mobility processes represented by the entire conditional distribution density of the children’s educational level given the parents’ level of education. In fact, the OV index statistically summarizes the existing differences, in terms of EOP or QOP, between the intergenerational mobility processes experienced by different countries. In this way, it is possible to provide evidence of the existence of a trend towards EOP or not.
Figure 2 shows the total OV index for each country during the period between 2003 and 2013. These indices were computed according to equation (1), for all children aged 25 to 64 years by birth cohort. The red bars represent the 95% confidence intervals for each estimated OV index.

Note: LB: lower bound of 95% confidence interval, UB: upper bound of 95% confidence interval. Source: Elaborated by the authors using data from Latinobarómetro.
Figure 2 Total OV Index for All Cohorts, 2003-2015
The countries were ranked from lowest to highest IOV obtained. While Guatemala has the highest IOV among Latin American countries (0.72), the lowest OV index in the region corresponds to Paraguay (0.429). However, this measure in Bolivia (0.44) and Ecuador (0.45) is not statistically different from that in Paraguay. The IOV of Mexico, El Salvador, Panama and Uruguay are slightly lower than the average value for all countries (0.54). While Colombia, the Dominican Republic and Costa Rica have rates very close to the average of the region. The IOVs in Nicaragua and Argentina far exceed the average but are not high enough to place these countries in the best positions in terms of equal educational opportunity. Chile and Honduras, for their part, are among the countries with the highest IOVs. But while the value obtained for Chile is statistically lower than that of Guatemala, the same is not true for the Honduras’ index. These results suggest that there is a great regional heterogeneity in the average levels of educational mobility between generations and, particularly, in equal opportunity in this dimension.
Figure 3 presents the OV index for each country according to the parents’ educational level with their 95% confidence intervals. These indexes allow us to examine the so called QOE hypothesis previously described. In other words, the comparison of the OV indexes for different socioeconomic groups makes it possible to evaluate whether public actions or equal opportunity policies were focused on improving the life chances of those who received a “poor inheritance” from their parents more than in diminishing the opportunity of those who received a “rich inheritance”. In this case, children whose parents have a very low educational level are considered “inherited poor” or from disadvantaged backgrounds while the children whose parents have completed higher education have more advantageous circumstances.

Note: LB: lower bound of 95% confidence interval, UB: upper bound of 95% confidence interval, PI: primary incomplete and CC: college complete. Source: Elaborated by the authors using data from Latinobarómetro.
Figure 3 OV Index by Parents’ Educational Level for All Cohorts, 2003-2015
Among Latin American countries, there is generally a trend towards greater equality of educational opportunity among children whose parents have the lowest level of education compared to those whose parents have the highest educational level. This suggests that most countries in the region have succeeded in increasing the mobility of the inherited poor compared to those from more advantageous family environment. Thus, in all countries, the OV index among children whose parents have an incomplete primary education level is significantly higher than that of children with parents that completed higher education. Therefore, the inter-generational educational mobility among the former remained closer to a situation of independence in relation to the family educational environment of origin than in the case of the latter. Among children whose parents have completed higher education, a greater index of educational mobility or independence regarding the paternal situation could suggest that the educational level reached by these generations was inferior to that of their parents.
On the other hand, in all countries the IOV corresponding to children whose parents did not complete primary educational level are higher than the total IOVs (see Figure 2) and vary from 0.71 to 0.95. The highest levels of equality of opportunity among children who come from more disadvantaged family educational environments are observed in Guatemala and Honduras (0.95). Chile and Argentina stand out for having the lowest values in this index (0.71 and 0.72, respectively). In Bolivia, Uruguay, Panama, Ecuador and the Dominican Republic, the IOV analysed is larger than that of Chile and Argentina, but similar to the average of the region (0.88). In the rest of the countries, however, this measure surpasses the average value, and although it is quite high, it is statistically inferior to the one observed in Guatemala and Honduras.
The IOV obtained for children whose parents reached the highest educational level vary from 0.31 to 0.62 among the countries of the region. The highest value is observed in the Dominican Republic and the lowest in Guatemala. This measure in countries like Colombia, El Salvador, Ecuador, Bolivia, Nicaragua and Brazil is close to the median (0.51) which coincides with the average index obtained in Latin America for children with parents who completed the upper educational level (0.50). In the rest of the countries this measure is inferior to the one of Dominican Republic, but the values of the IOV between them are not significantly different from one another.
The results also reveal that the gaps between IOVs of children whose parents reached the highest educational level and those who have parents with incomplete primary education differ among countries. Thus, the greatest differences in these measures are seen in Honduras, Guatemala and Paraguay. Argentina, on the other hand, stands out for presenting the lowest gap between the countries of the region.
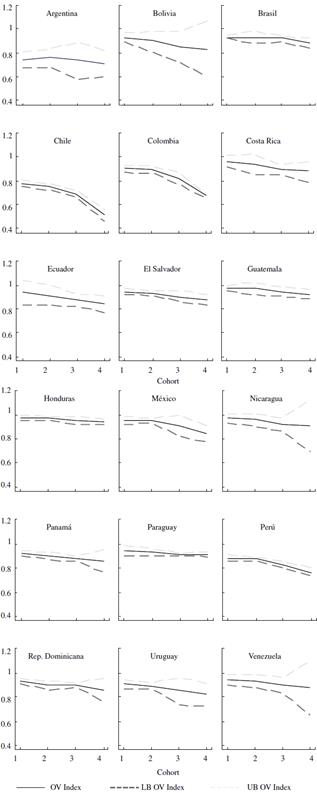
On the other hand, the available data allow us to examine not only the average level of IOV during 2003-2013, but also its evolution in each of the Latin American countries considered. From this analysis it is possible to evaluate if countries experienced improvements in the levels of equal educational opportunity, not only in the population as a whole, but also among those who come from the most disadvantaged family environments. Figure 4 presents the evolution of the OV index along birth cohorts by country.

Note: LB: lower bound of 95% confidence interval, UB: upper bound of 95% confidence interval. Source: Elaborated by the authors using data from Latinobarómetro.
Figure 4 OV Index by Cohort and Country, 2003-2013
In most of the countries of the region (Argentina, Bolivia, Brazil, Colombia, Costa Rica, Ecuador, Panama, Peru, Dominican Republic, Venezuela and Uruguay) the IOV increases from the older cohorts towards the younger. However, not all of these countries show the same increase in IOV along birth cohorts. Thus, in ascending order, Argentina, Peru, Uruguay and Venezuela show the highest increases in this measure between the youngest cohort and the oldest cohort, varying from 20 to 25 percentage points. According to the estimates reported in the Table A1 these differences are statistically significant at 1%. At the other extreme is Guatemala, which stands out for the substantial worsening of this measure between the first and last cohort considered.
While the increase in IOV suggests an improvement in the average levels of equal educational opportunity in the region, it is also important to examine whether this result is primarily a consequence of increased educational mobility among children from disadvantaged backgrounds, or rather responds to IOV growth among those whose parents have the highest educational levels. According to Figure 5, there is no increase in the OV index for children whose parents have incomplete primary education according to birth cohort in any of the countries of the region.
Note: LB: lower bound of 95% confidence interval, UB: upper bound of 95% confidence interval. Source: Elaborated by the authors using data from Latinobarómetro.
Figure 5 OV Index by Country and Cohort for Children Who Have Parents with Incomplete Primary Education, 2003-2013
In contrast, in most countries, specifically in Brazil, Chile, Colombia, Costa Rica, El Salvador, Guatemala, Honduras, Mexico, Peru and Uruguay, there is a considerable reduction in IOV when comparing older and younger cohorts of the children whose parents did not complete primary education. In addition, in the rest of the countries, although there is a drop in the index examined, this is not statistically significant. Therefore, these results suggest that the increase in overall IOV over time observed in most countries in the region does not respond to an improvement in the equality of opportunity or in the educational mobility among the children who come from the most disadvantaged family environments.
It is therefore of interest to examine the evolution of the OV index among children with parents who completed college (see Figure 6). In contrast to what is observed in Figure 5, several countries show a growth in this measure when we move from the older cohorts to the younger. But this increase is statistically significant in Argentina, Chile, Costa Rica, Ecuador, Nicaragua, Panama, Peru and the Dominican Republic. In contrast, in Uruguay and Paraguay the index examined remained roughly stable throughout the cohorts.

Note: LB: lower bound of 95% confidence interval, UB: upper bound of 95% confidence interval. Source: Elaborated by the authors using data from Latinobarómetro.
Figure 6 OV Index by Country and Cohort for Children with Parents Who Completed College, 2003-2013
From the estimates in Tables A1 it is observed that in the majority of the countries that show a significant increase in their general average level of equal educational opportunity, according to the IOV, the children whose parents finished high school are the ones that present the most important increases in this indicator between the oldest and the youngest cohort. These increases range from 14.7 percentage points in Chile to 47.5 percentage points in Venezuela. In Argentina and Peru, on the other hand, children with parents with higher education are those who exhibit the greatest increases in the OV index. In the Dominican Republic, those with parents who finished high school show the highest increase in that indicator and there-fore seem to have experienced the main improvements in terms of equal opportunity and educational mobility. It should also be noted that in none of the countries with a statistically significant increase in total IOV between the oldest and youngest cohort, is there a growth in this indicator among children from the most disadvantaged educational environments; that is to say, those with parents who did not finish high school. Moreover, in most of these countries, the IOV corresponding to these groups declined.
CONCLUSIONS
The main objective of this research was to analyse the level and trends of inter-generational educational mobility in Latin America during the three decades that separate the cohorts born in the 1950s from those born in the 1980s. The analysis focused primarily on assessing the evolution of IME from the equal opportunity approach. The central question to answer is to what extent the changes observed in the process of intergenerational mobility modified the levels of equal opportunity in each country, particularly among the most disadvantaged socio-economic groups. To this end, a new technique proposed by Anderson et al. (2014) was implemented which consists of measuring the degree of overlap between the conditional density of the children’s education given the parents’ education and the theoretical density corresponding to a situation of EOP or independence bet-ween the two variables. This technique has several advantages over other existing methods, among them, to offer a measure - the OV index - that allows us to not only evaluate the existence of equal opportunity, but also the progress made by society in this dimension. In addition, from this technique it is possible to evaluate the so-called QEO hypothesis, i.e. if children who benefited most from the EOP point of view are those who belong to the most disadvantaged groups due to his parents’ low educational levels.
The results obtained in most Latin American countries show an improvement in EOP average levels among the younger generations. However, there is a notable lack of improvement in EOP levels, as measured by the OV index, among children of parents with the lowest levels of education. But it is also generally observed for several generations that IEM among children of parents with lower education levels remained closer to a situation of independence or EOP than in the case of those whose parents completed higher education. Nevertheless, the relative stability of the OV index among the children of the most disadvantaged educational group suggests that, in several countries in the region, public policies were not effective enough to improve equal educational opportunity between them.
One of the central questions that emerges from the results of this research is related to the factors that may explain the observed drop in intergenerational educational persistence and the increase in general levels of EOP among the younger cohort considered in comparison with the biggest. According to the theoretical model of Solon (2004), public investment in the human capital of children and adolescents is a central factor in the process of intergenerational transmission of socioeconomic status. The analysis of the effects of this and other variables on the intergenerational mobility and the levels of EOP observed in Latin America constitutes an interesting line for future research.



















