PURPOSE OF THE THEORY OF VALUE AND LIMITS OF THE REAL AND STRICTLY MONETARY APPROACHES

The general economic problem that any social system faces consists of how to determine what, how, how much, when, and where people will produce and consume at any given moment. In market societies, these issues are decided by all economic agents in a decentralized manner without any a priori coordination. The economy is organized in markets so individuals can specialize and exchange the product of their economic activities, and the adjustment of prices is expected to prevent these activities from being systematically incompatible (^{Klimovsky, 2000}).

This kind of social system raises several questions. For example, under what conditions can the price mechanism coordinate all economic activities? Are markets self-regulating or do they always tend towards crises? How do different kinds of incomes evolve? And ultimately, will this economic system be able to solve the various problems that humanity currently faces (such as environmental problems, economic inequality, etc.)?

Theory of value aims to answer these questions from a general (and therefore abstract) standpoint, first analyzing the logical conditions under which prices can function as a coordination mechanism of market societies, and then analyzing the logical implications that this functioning may have concerning other aspects of interest such as those just mentioned (environmental problems, economic inequality, etc.).

Now, assuming a veil of ignorance of the current state of theories of value in all their approaches, let us consider the minimum theoretical aspects that a theory of value should have to satisfactorily explain the price system working in market societies.

First, an explanation must start from a disaggregated description of the economy in terms of individuals and commodities. This is because aggregate analysis of the economy eliminates the coordination problem that the price mechanism must solve, and the theory of value must explain¹.

Secondly, the interdependent relations that exist between consumption and production activities must be made explicit, since, if these relations are not specified, it will never be possible to know whether prices can or cannot be an effective mechanism for coordinating these activities.

Third, the minimum institutional framework that allows individuals to act in market societies must be specified. Within this institutional framework, a fundamental element is money and the monetary system since a barter system is not compatible with decentralized exchanges.

Next, the mechanisms by which the market economy works (how supply, demand, prices, and exchanges are determined and adjusted) must be specified in detail. It is important to emphasize that, in market societies, economic activities such as exchanges, production, and consumption take place continuously, regardless of whether the economy is in equilibrium or not.

And finally, it is necessary to show the conditions under which price adjustment can, or cannot, regulate disequilibrium. In other words, the theory must identify the conditions under which the adjustment process occurring in the model is stable or non-explosive, in the sense that any imbalance that appears decreases or, at least, does not increase over time.

Note that once these requirements are met, the other problems posed by this type of social organization, such as wealth distribution, environmental problems, etc., can then be analyzed. It is naïve to try to give a scientific answer to these normative and practical aspects without first having a logically coherent theory of value. Hence the importance of theories of value for the science of market societies.

Limits of the real approach to the theory of value

The canonical models of the real approach to the theory of value are the neoclassical general equilibrium model (^{Arrow & Debreu, 1954}) and the classical-Marxian production prices model (^{Sraffa, 1966}), as well as the neoclassical disequilibrium model of Walrasian tâtonnement (Arrow et al., 1959) and the classical-Marxian disequilibrium tâtonnement models of gravitation² (^{Boggio, 1985}).

Assuming that the main results of these models are known to the reader³, it can be said that they only fulfill the first and second requirements mentioned above, but not the third, fourth, or fifth, because 1) the exclusion of money implies that the decentralized functioning of markets be left aside (^{Ostroy & Starr, 1974}), so the prices explained by this approach do not result from market economies; 2) the positive price of money cannot be explained by the theory of value (^{Benetti, 1990}), so the results obtained by this approach cannot be attributed a posteriori to a monetary economy; 3) except in very particular cases, money is not neutral (^{Lagos & Wright, 2005}), so the results obtained by this approach will not generally be equivalent to those resulting from monetary economies either; and 4) the tâtonnement process depends on a centralized mechanism that is also incompatible with the market society. For all these reasons, it can be concluded that the real approach to the theory of value is logically incapable of explaining its object of study.

Limits of the strictly monetary approach to the theory of value

The strictly monetary approach is formed by a small group of heterodox monetary theories that all construct a theory of value without reference to the real sector, namely, the theories proposed by ^{Benetti and Cartelier (1980}), Aglietta and Orléan (1982, 2002), and Cartelier (2018).

The starting point for the strictly monetary approach was ^{Benetti and Cartelier's 1980} study. In this study, they take on the problem posed by the theory of value directly and try to find a solution in exclusively monetary terms. This, because they consider commodities to be of no analytical interest due to the fact that 1) they are the result and not a condition of market relations (they criticize the nomenclature hypothesis which presupposes the existence of a commodity space independent of the functioning of the market); and 2) capitalist production activities are inaccessible to economists because they are carried out in the "secret laboratories" of capitalists, so this knowledge could not be obtained even if it were of interest to economists.

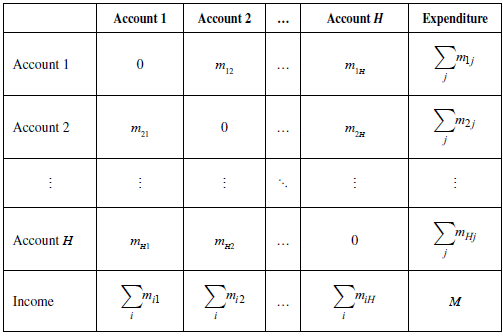
For this reason, this approach conceives market societies as a system of individual monetary accounts, interrelated by the monetary payments that occur between them, and which are expressed analytically through the following matrix (Table 1).

Table 1 Monetary payment matrix 

Where ≥ 0 (with i, j = 1,..,H) is the amount of money that account i pays to account j, as a counterpart of the purchase of a commodity on a given date. If money is fiat, money enters the matrix in the form of credit offered to individuals by the monetary authority and leaves it when individuals repay this debt. On the other hand, if money is anchored to the quantity of a standard commodity, then the monetary institution sets a legal price for this commodity, and money enters the payment matrix when individuals sell their stocks of this commodity to the monetary institution and leaves when they buy these stocks (Aglietta & Cartelier, 2002). Thus, the monetary authority can control this quantity by manipulating the monetary interest rate, in the first case, or the legal price of the standard commodity, in the second case.

In a credit market economy, individuals borrow money to finance their expenses before obtaining income from the sale of their products. To calculate the amount of a requested loan, individuals rely on their income expectations. One of the characteristics of disequilibrium is that not all individual expectations are fulfilled. Therefore, during disequilibrium, there are always individuals who have negative or positive balances of money, with the sum of these balances always equal to zero (since aggregate income is equal to aggregate expenditure, represented in the payments matrix by the letter M).

These balances need to be regulated so that debtors meet their obligations by transferring wealth to creditors (^{Cartelier, 2009}). However, if the punishment of deficit holders is not severe enough, it will discourage surplus holders from keeping their wealth in monetary form, which may unleash inflationary pressure. On the other hand, if the punishment is too severe, it may cause a contraction of aggregate demand, affecting the whole economy (Aglietta & Orléan, 1982, 2002).

Thus, the dilemma that any monetary authority faces is the question of how to formulate balance settlement rules that satisfy these two aspects of the same problem: on the one hand, to avoid a recession crisis by allowing debtors to settle their debt and remain in the system and, on the other hand, to avoid an inflation crisis by giving individuals with a positive balance a return on their balances that satisfies their expectations. The 'viability theory' (^{Cartelier, 2018}) analyzes this dilemma in dynamic terms.

This explanation, while brief, is sufficient to demonstrate that the strictly monetary approach completely satisfies only the first and third requirements mentioned above (namely, disaggregated description and consideration of the institutional aspects of the economy-particularly money-), and the monetary aspect of the second, fourth, and fifth requirements of the theory of value (consideration of the monetary relations of interdependence through the payments matrix, specification of the dynamics in monetary terms and its analysis through the theory of viability). It does not, however, satisfy the real dimension of these last three requirements, since the relations of interdependence that exist between the individual activities of consumption and production are not considered, nor are the dynamics specified in real terms, and the conditions of their convergence to equilibrium are not analyzed.

This is a problem because although the objects of final consumption may be the result of a specific market performance, such objects can only be produced by satisfying the terms of certain technical relations with other objects which are independent of market relations at a given moment in time. The theory of value must explain how the price mechanism can or cannot satisfy the terms of these interdependent relations over time. These terms must be satisfied in order for the productive activities to continue to function. If production activities were to decrease or even cease, this would jeopardize the very existence of society, regardless of the circumstantial objects of final consumption produced in the economy.

In other words, every social system has a set of technically viable productive methods that establish relations between economic objects, the terms of which must be satisfied in order for the objects to be produced. These relations are characterized as real, non-monetary and independent of the social system, and are a fundamental aspect of the relations of interdependence that exist in any social organization and, therefore, are a central part of the coordination problem posed by the functioning of the price system. However, by using a strictly monetary analytical framework which leaves these relations to one side, this approach cannot provide an answer to the problem of coordination, as was later recognized by ^{Benetti and Cartelier (2013)}. A strictly monetary analytical framework, then, cannot be a coherent approach to the theory of value either.

This section has shown that a coherent approach to the theory of value must be framed in a microeconomic model of disequilibrium, in which the monetary and non-monetary relations of economic interdependence between individuals and their activities are made explicit. This model must also show the conditions under which the price system can (or cannot) coordinate economic activities and their interdependent relations.

THE CLASSICAL AND MARXIAN MONETARY APPROACH TO THE THEORY OF VALUE

The monetary models of the classical-Marxian theory of value have a much more recent history. They began to appear in the 1980s with the emergence of models that tried to formalize classical-Marxian gravitation theory. Broadly speaking, this theory of value postulates that when market prices do not guarantee a uniform rate of profit, they cannot remain fixed, since differences in profit rates will encourage capitalists to transfer their capital from the less profitable sectors to the more profitable ones, thus altering the productive structure of the economy and market prices. This process of adjustment will stop only when the prices that guarantee uniform profit rates (the equilibrium prices of the classical-Marxian approach to the theory of value) are reached.

Although there are differences between Smith, Ricardo, and Marx on this issue, the literature usually encompasses the different formalizations made in this field as gravitation models (^{Carminati, 1990}). Most of them are non-monetary and tâtonnement models. To the best of our knowledge, only three types of gravitation models stand out as being monetary and non-tâtonnement, namely: those of ^{Nikaido (1983}; 1985)⁶, ^{Duménil and Lévy (1983}; 1990a; 1990b) and ^{Benetti et al. (2014}; 2015).

These three models share the following assumptions: the economy is monetary and bi-sectoral; wages are given and paid ex-ante in physical terms; each branch produces a single commodity with a single method of production, using both goods as productive inputs in fixed proportions and under constant returns to scale. We will now examine the particularities of these three models.

Nikaido analyzes Marx's gravitation theory through two disequilibrium models, the only difference between them is that in one, he assumes simple reproduction, and in the other, expanded reproduction. Despite this difference, both models share the same hypotheses: the accumulation rate of each capitalist is exogenously given (it is zero in the first model and a constant proportion of their income in the second). Nevertheless, the amount of money that capitalists invest in each branch depends on the differentials of their profit rate, where: if the rate of profit is higher in branch 1 than in branch 2, at the next date the amount of money invested in branch 1 will increase at the expense of branch 2 concerning the previous period, etc. The monetary institution is a pure cash system, meaning that the amount of money spent by capitalists in each period is equal to their income at the previous date. Prices are determined by two alternative rules: the rule of temporary equilibrium (supply equals demand on each date) and the following temporary disequilibrium rule: commodity prices are those which match the value of capital with the monetary amount of investment.

The two Nikaido models show that, if the capital composition of branch 1 is lower than that of branch 2, the adjustment processes of both models converge to equilibrium, that is, market prices 'gravitate' to production prices. Otherwise, the process diverges in the sense that market prices move indefinitely away from production prices.

Nikaido's two models have several problems: 1) the hypotheses are quite specific, which shows the narrow limits of his results: his models are bi-sectoral, with only one method of production, no fixed capital, no rent, etc. and it is not evident that generalizing such hypotheses would yield the same results; 2) the absence of a theorized behavior for capitalists that would explain how their consumption and investment decisions are determined; 3) the mechanism of capital mobility lacks micro-foundations (if branch 1 yielded a higher rate of profit than branch 2, and if all capitalists have this information, why do capitalists not invest all their capital in branch 1? Why is there a non-zero investment in branch 2?); 4) both rules for determining prices are incompatible with market societies because they are centralized: the equations system to calculate prices in both rules can only be solved by considering the interdependence relations among the whole economy, and 5) the pure cash monetary system is one of the two extreme cases in which any actual economic monetary system is found⁷. Therefore, Nikaido's monetary hypothesis is very particular, and there is no evidence to suggest that generalizing it would give the same results.

In Duménil and Lévy's model, they propose an alternative formalization of the Marxist gravitation theory which, in addition to the basic characteristics already mentioned, they set the accumulation rate at zero. However, capitalists allocate their capital in each branch according to the differentials in sectoral profit rates; branch 1 produces a durable good (fixed capital), so now the economy is a joint-production system. The prices of each commodity are set by the capitalists in each branch using the following rule of price adjustment: the price varies in proportion to the difference between the actual and the desired stock of each commodity held by the capitalists in their warehouses; the economy works through a credit monetary system (there is a banking system which captures the savings of consumers and lends to producers at a zero interest rate and according to the differentials of the sectoral profit rates).

The authors show that, under certain conditions which concern the reaction coefficients of prices and quantities, the dynamics of their model converge to production prices. However, in addition to the assumptions criticized above made by Nikaido in his model which this model reproduces, the Duménil and Lévy model has the following two additional problems:

First, the theoretical indeterminacy of their rule of price adjustment. This rule depends on two parameters: 1) the desired stock of goods and 2) the coefficient that relates price variation to the difference between the actual and desired stock of goods. The problem with these two parameters is that both are, on the one hand, arbitrary (in the sense of being theoretically unjustified) and, on the other hand, fundamental to the stability results, which makes their model uninteresting.

And, secondly, the Duménil and Lévy model does not consider the regulation of monetary balances that may appear during disequilibrium, due to the existence of credits in the economy. This situation puts the whole monetary system in conflict, meaning that institutional rules must be specified to allow the settlement of these monetary balances to reestablish ex post the budget constraint of individuals. However, Duménil and Lévy are silent on the matter.

^{Benetti et al. (2014}; 2015) do specify a monetary balance settlement rule in their models. In addition to the basic features already mentioned, these models assume that: 1) capitalists accumulate all their income and reinvest it in their branches (Benetti et al. criticize the mechanism of capital mobility between branches to explain the adjustment of quantities and reject it for lacking micro-foundations); 2) prices are formed by a perfectly competitive market mechanism called the 'Cantillon rule' (under which the prices of each commodity are determined by dividing the quantities of money and commodity brought to the market to be exchanged); 3) the monetary framework is a pure credit system issued by a bank (credit is issued at the producer's request, and the producers commit to reimburse the bank immediately after the exchange); 4) the monetary balances appearing in disequilibrium are settled by the following rule: the capitalist with a positive monetary balance gives his balance to the capitalist in the red in exchange for a basket of commodities whose monetary value is equal to the monetary balance (evaluating the goods at their market prices) and whose physical composition is chosen by the agent with a positive monetary balance.

The authors of this model show that the balance settlement rule can be unfeasible in certain cases, which they call "pathological". But, when these cases are excluded⁸, the dynamics to which the economy gives rise are non-explosive, in the sense that the adjustment process converges to equilibrium or to a cycle of order two, in which market prices 'gravitate' around equilibrium prices.

However, in addition to the assumptions criticized above from the Nikaido and Duménil and Lévy models that the Benetti et al. model reproduces, it has the following two additional problems:

First, the balance settlement rule that they assign, as well as being unrealistic and naïve, is very restrictive in two different senses: 1) its feasibility can only be guaranteed when the property described in footnote 8 is met, meaning that this condition is quite strong for a market society (because, due to the social division of labor, one would expect that in these societies inter-industrial dependence would be significantly higher than intra-industrial dependence), and 2) the balance settlement rule can only be used when the model is set in a bisector economy, since in an economy with n sectors, with n > 2, there may be compatibility problems between the accumulation plans of capitalists with positive monetary balances and the availability of commodities produced by capitalists with monetary deficits.

A second problem is that the Cantillon rule is a very particular market mechanism that is not used in any actual market (as other market mechanisms such as the double auction or the first price sealed-bid auction are used); and there is no evidence to suggest that the same stability results could be obtained using these alternative market mechanisms, or individual pricing rules under imperfect competition.

Thus, this section can be concluded by stating that none of the classical-Marxian monetary models of the theory of value reviewed here are completely satisfactory, due to the specificness of their hypotheses that make their results very limited in scope.