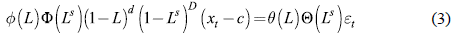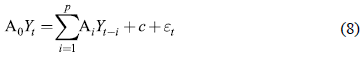INTRODUCCIÓN
Para el análisis del sistema productivo de un país es fundamental tener la evidencia empírica macroeconômica y microeconómica. Por un lado, el análisis macro permite identificar los principales factores que afectan a la demanda y la oferta agregadas. Por otro lado, la microeconomía nos permite comprender el comportamiento de las empresas, hogares e individuos (agentes económicos). Ambas hacen posible desarrollar una visión completa de la economía en cuestión que permite que el gobierno diseñe política pública y los agentes económicos tomen decisiones acertadas para su bienestar (Agénor y Montiel, 2015).
Los países en desarrollo han sufrido de problemas para obtener datos agregados de alta frecuencia (trimestral, mensual, semanal o diaria) que permitan un análisis concordante con la teoría económica (Agénor y Montiel, 2015). Los cambios de metodología o institucionales han provocado ruptura en los datos que dificultan un análisis completo de sus economías.
En el caso de Ecuador, además de estos problemas, en el año 2000 se instauró la dolarización de la economía, lo que produjo un quiebre en todo el análisis económico del país y tornó más compleja la comparación de los datos macroeconómicos1 (Díaz, 2018). Gachet et al. (2013) evidencian tal dificultad de obtener datos agregados (series de tiempo) de alta frecuencia para un análisis macroeconómico empírico (econométrico) del mercado laboral del Ecuador debido a que solamente tenían una muestra anual entre 2000-2010 (once observaciones). Los mismos autores indican que se podrían utilizar estadísticas aproximadas del área urbana o del sector formal, aunque no necesariamente representarían la dinámica nacional. En contraste, estudios como Carrillo-Maldonado (2017) o González-Astudillo y Baquero (2019) muestran que la generación de datos de alta frecuencia (mensuales y trimestrales) permite realizar un análisis concordante para la economía ecuatoriana dolarizada.
Actualmente, el Instituto Nacional de Estadística y Censos (INEC) publica datos anuales del mercado laboral, desde el 2007, y trimestrales con representatividad nacional y concordancia muestral, desde el 2014, lo que significa que se tiene un número reducido de observaciones para realizar un análisis econométrico del mercado laboral ecuatoriano2. Esta situación, a su vez, dificulta la inferencia estadística, pues se reducen los grados de libertad por cada variable explicativa, la inclusión de rezagos (retardos) de las variables o la transformación de las variables para obtener estacionariedad (primera o segunda diferencia).
En la presente investigación se busca cubrir esta brecha, dado que, según la revisión de la literatura hecha, no existe un análisis macroeconómico empírico del mercado laboral ecuatoriano3. Si bien se han incluido variables laborales en modelos de proyecciones (véanse González-Astudillo y Baquero, 2019), estos han utilizado técnicas de interpolación (por ejemplo, Chow-Lin o modelos estado-espacio) con variables proxy (por ejemplo, desempleo urbano) para acoplar a la frecuencia (trimestral o mensual) del resto de variables.
En ese sentido, el objetivo de este artículo es proveer un método y datos trimestrales del mercado laboral entre el 2007 y el 2019, con base en la Encuesta Nacional de Empleo, Desempleo y Subempleo (ENEMDU) del INEC. Para ello, se propone una corrección econométrica de los datos trimestrales que no tienen representati-vidad nacional (mediante la detección de cambios estructurales) llamada "ajuste por outliers identificados".
La idea intuitiva es hacer una interpolación exclusivamente en las observaciones identificadas que no tienen representatividad nacional, desde el concepto muestral, debido a la recolección de datos en la ENEMDU. Para evidenciar la validez de los resultados, los datos ajustados con esta corrección se incluyen en un modelo de vectores autorregresivos estructurales (SVAR, structural vector autoregressive model), típico en la literatura macroeconómica, donde intervienen variables del mercado laboral (véanse Blanchard y Quah, 1989; Dolado y Jimeno, 1997; Galí, 1999).
La principal contribución a la literatura consiste en evidenciar que, a pesar de que, en algunos periodos, la muestra no posea representatividad nacional, esta permite obtener datos trimestrales agregados que sirven para un análisis empírico de la economía ecuatoriana gracias al ajuste de outliers identificados.
Granda et al. (2017) proponen ejercicios metodológicos, en la perspectiva mues-tral, que permiten obtener datos comparables del mercado laboral desde el 2003 en adelante, dada la ruptura conceptual de las series de tiempo de las variables de empleo que se produjo en la ENEMDU en 20074. Aquí se propone utilizar datos trimestrales desde el 2007 que permiten obtener series de tiempo que no tienen rupturas en el periodo 2007-20195.
Además, se propone un primer modelo empírico con variables del mercado laboral que hacen posible un análisis estructural macroeconómico del Ecuador que hasta el momento no existe en la literatura. La estimación del modelo SVAR con las variables ajustadas se contrasta con la típica corrección de Chow y Lin (1971) de interpolación de series de tiempo. Los resultados muestran que la propuesta aquí presentada ofrece resultados coherentes con la literatura, mientras que la interpolación podría mostrar resultados no convencionales para el caso ecuatoriano.
El artículo tiene la siguiente estructura: la segunda sección presenta la descripción de la ENEMDU, la construcción de los datos agregados del mercado laboral, con y sin representatividad nacional, y los cambios estructurales atados a cambios en el diseño de la encuesta. La tercera sección muestra el modelo empírico con las variables laborales y los resultados obtenidos. La cuarta sección expone las conclusiones.
CONSTRUCCIÓN DE ESTADÍSTICAS DEL MERCADO LABORAL ECUATORIANO
La Encuesta Nacional de Empleo, Desempleo y Subempleo es una encuesta por muestreo probabilístico, cuyo objetivo es proveer información sobre la actividad económica y las fuentes de ingresos de la población. La ENEMDU está diseñada para proporcionar estadísticas sobre los niveles, tendencias y cambios en el tiempo de la población económicamente activa (PEA), población económicamente inactiva (PEI), el desempleo y otros indicadores relevantes de mercado laboral del Ecuador, con representatividad nacional, urbana, rural y cinco ciudades principales (Quito, Guayaquil, Cuenca, Machala y Ambato) (véase INEC, s. f.).
El levantamiento de datos relacionados con el mercado laboral se inició en el año 1985, con la creación del Instituto Nacional de Empleo (INEM), adscrito al Ministerio de Trabajo. En noviembre de 1987, se dio el primer levantamiento de información de la Encuesta Permanente de Empleo y Desempleo, la cual tuvo representatividad urbana y periodicidad anual (véase INEC, 2011). A partir de 1993, la ENEMDU fue realizada por el Instituto Nacional de Estadística y Censos y financiada por el Banco Central del Ecuador (BCE). La representatividad de esta encuesta fue urbana y, hasta 2002, se desarrolló de manera anual. A partir de septiembre de 2003, se implementó la ENEMDU de manera trimestral. Desde esa fecha, hasta el año 2013, se utilizó como marco muestral el VI Censo de Población y el V de Vivienda (CPV) de 2001 (INEC, 2011). En la Tabla 1, se detalla la periodicidad y la desagregación de la ENEMDU desde el 2003 hasta el 2007.
En el año 2007, se introdujeron algunos cambios metodológicos a la ENEMDU que produjeron la ruptura de las series de los indicadores generados a partir de ella. Dichos cambios fueron los siguientes: incorporación de algunas recomendaciones sobre la producción de estadísticas laborales de la Organización Internacional del Trabajo (OIT); armonización de las estadísticas para la integración de la Comunidad Andina de Nacionales (CAN); y armonización de las estadísticas publicadas por varias organizaciones, entre ellas el INEC y el BCE (Granda et al., 2017).
Algunos de los cambios principales que se efectuaron en el año 2007 tienen que ver con el formulario de recolección de información, que es la herramienta para clasificar a las personas en población económicamente activa, inactiva, empleada y desempleada.
Así, en dicho formulario se realizaron cambios en los flujos y las preguntas sobre los siguientes temas: 1) el deseo y la disposición de trabajar más horas (para la población con empleo); 2) el periodo de referencia en la búsqueda de trabajo (para la población con desempleo); 3) la reestructuración de las categorías de la pregunta "¿razón por la que no buscó trabajo?" (para la población desempleada e inactiva); entre otros cambios (Granda et al., 2017).
Como consecuencia de esta revisión del marco conceptual, existe una ruptura de las series desde el año 2007 (Tabla 2).
A partir de septiembre de 2013, se inició una migración gradual de la muestra de la ENEMDU que tomaba como marco de muestreo el CPV del 2001 a un marco de muestreo basado en el CPV del 2010. Este proceso culminó en diciembre de 2013. Y desde 2014 toda la encuesta utiliza el marco de muestreo actualizado con la información del último CPV (INEC, 2013a). Según el INEC, esta actualización no produjo una ruptura de las series en el año 2014, por lo que la información de la ENEMDU es comparable desde el 2007 en adelante (INEC, 2013b).
Tabla 2 Periodicidad y cobertura de la ENEMDU (2007-2019)

Fuente: INEC (2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019).
AJUSTE POR OUTLIERS IDENTIFICADOS
Métodos de desagregación temporal
Los métodos de desagregación temporal se utilizan para obtener una serie de tiempo de alta frecuencia (mensual o trimestral), con base en una variable temporal de baja frecuencia (anual o semestral). Este proceso garantiza que la suma, el promedio, el primer valor y el último valor de la serie de alta frecuencia sean acordes con la serie de baja frecuencia. Esta desagregación temporal se puede realizar con uno o más series de indicadores de alta frecuencia. Incluso, cuando no hay una serie de indicadores de alta frecuencia, es posible realizar la desagregación con métodos de interpolación. No obstante, en este caso, la precisión de la serie de alta frecuencia resultante podría ser baja, pues no iría necesariamente de la mano del comportamiento del indicador (Sax y Steiner, 2013).
Dentro de los métodos más utilizados se encuentran los de Denton, Denton-Cho-lette, Chow-Lin, Fernández y Litterman. Por un lado, las variantes del método de Denton (1971) consideran la preservación del movimiento y generan así una serie similar a la serie de indicadores de alta frecuencia. Estos métodos también pueden realizar la desagregación sin la necesidad de un indicador (Dagum y Cholette, 2006). Por otro lado, métodos como los de Chow-Lin, Fernández y Litterman utilizan uno o varios indicadores, y realizan una regresión sobre la serie de baja frecuencia. El método de Chow y Lin (1971) es adecuado para series estacionarias o cointegradas, mientras que los de Fernández (1981) y Litterman (1983) sirven para series temporales no cointegradas6.
Estos tipos de métodos para desagregación temporal se utilizan ampliamente en países europeos para las estadísticas oficiales. La mayoría de las autoridades europeas estadísticas, por ejemplo, utilizan estos métodos para la estimación de los indicadores trimestrales del producto interno bruto (PIB) (véanse Sax y Steiner, 2013). Para el caso ecuatoriano, Carrillo-Maldonado (2017) utilizó el método de Chow-Lin para obtener el PIB ecuatoriano con una frecuencia mensual sobre la base de un índice coincidente de actividad económica, para luego incluir esta variable de alta frecuencia en un modelo SVAR con cambios de regímenes.
Según Sax y Steiner (2013), los métodos de desagregación temporal se pueden resumir en un proceso de dos pasos: primero, se debe determinar una serie de alta frecuencia preliminar p; y, segundo, las diferencias entre los valores agregados de la serie preliminar y el valor agregado de la serie de baja frecuencia deben distribuirse. La agregación de las series preliminares y los residuos distribuidos arrojan la estimación final de la serie final, ŷ):
Donde D es una matriz de distribución nxn l y u l es un vector de longitud n l que contiene las diferencias entre los valores anualizados de p y los valores anuales reales y l . Además, n y n l denotan el número de observaciones de alta y baja frecuencia, respectivamente.
Donde c es la matriz de conversión de alta a baja frecuencia de dimensión n l xn. La ecuación (1) constituye un marco unificador para todos los métodos de desagregación. Los métodos difieren en como determinan la serie preliminar p y la matriz de distribución D (véanse Sax y Steiner, 2013).
Propuesta metodológica
Para la corrección econométrica se utiliza el programa X13-ARIMA-SEATS, del U. S. Census Bureau (2017), que permite ajustar la estacionalidad y detectar datos atípicos (outliers), entre otras correcciones7. Este enfoque no paramétrico permite estimar los componentes no observados de una serie de tiempo, sin tener que recurrir a la especificación de un modelo estadístico para la serie de tiempo analizada. Por ello, este tipo de procedimiento también se conoce como enfoque empírico.
En este enfoque, los componentes se estiman mediante la aplicación sucesiva de filtros lineales, interpretados como regresiones locales en intervalos móviles en el tiempo (Villareal, 2005). Desde Box y Jenkins (1970), los modelos ARIMA se utilizan para hacer el ajuste estacional en las variables de series de tiempo. Un modelo ARIMA general multiplicativo con estacionalidad y componentes deter-minísticos se expresa así:
Donde x t es la variable del mercado laboral en análisis; c es el vector de componentes determinísticos (constante, tendencia, etc.); ε t es el residuo con media cero y varianza σ2 (ruido blanco); L es el operador de rezagos (Lx t = x t - 1 ); s es la periodicidad del componente estacional; ф (L ) y Ф (L s ) son los operadores autorregresivos no estacional y estacional; θ(L) y Θ y (L s ) son los operadores de media móvil no estacional y estacional; (l - L) d y (l - L s ) D - son los operadores de diferenciación del componente autorregresivo y estacional.
El modelo de la ecuación (3) se puede estimar usando diferentes métodos, como mínimos cuadrados o máxima verosimilitud. El modelo tiene la flexibilidad de incluir variables tanto determinísticas como estocásticas para obtener el mejor ajuste de la variable de interés. Así, se puede analizar la existencia de datos atípicos en la muestra.
Además, este método puede considerar, en el proceso de ajuste de las series, los efectos de días feriados y de calendario. En este trabajo se hace una detección de ou liers para determinar si existe un cambio de comportamiento en las variables del mercado laboral, debido a que se hicieron cambios en el levantamiento de la información de la ENEMDU que tienen efecto sobre la representatividad de la muestra encuestada.
En el vector c se incluyen variables dummies para detectar cambios de nivel (level shifts, LS) y datos atípicos aditivos (aditive outliers, AO). Estas variables se construyen así:
Donde to es el punto en el tiempo en el que se evalúa la existencia de un outlier. La detección de datos atípicos se hace de manera iterativa en todos los puntos en el tiempo t = 1,..., T.
Como ya se mencionó (Tabla 2), la ENEMDU no tiene representatividad nacional en los meses de marzo y septiembre entre 2007 y 2013; mientras que, para el resto del periodo muestral, sí tiene representatividad.
Por ello, además, para los meses en los que no existe representatividad nacional, se implementan variables dummies del tipo additive outlier en el modelo de la ecuación (3), pues el quiebre por no representatividad existe exclusivamente en dicho trimestre. En contraste, no se incluye como dummy del tipo level shift, pues este outlier no es permanente en la serie de tiempo. Estas variables se expresan así:
Donde tr 1t y tr3 t son las variables dummies para los meses de marzo y septiembre en el periodo muestral que no tiene representatividad nacional (NR) (2007-2013). Se estima el modelo de la ecuación (3) incluyendo las variables dummies de outliersy de no representatividad (tr1t y tr3 t ) con el método de máxima verosimilitud. Además, se emplean los criterios de información y las funciones de autocorrelación y correlación parcial para determinar el número de rezagos autorregresivos, de media móvil y de diferenciación.
Variables del mercado laboral ajustadas
A continuación, se presentan las variables del mercado laboral ajustadas por outliers y por los datos que no tienen representatividad. Este ajuste se aplica en el número de personas de la población económicamente activa (PEA), con empleo, en las tasas de desempleo y de empleo adecuado y en el salario nominal promedio en dólares. La metodología antes descrita se puede implementar también en otros indicadores de la ENEMDU (desigualdad, pobreza, etc.).
Además, de la propuesta de ajuste por outliers identificados, se presentan otros métodos (como Chow-Lin y ajuste automático). En la interpolación con Chow y Lin (1971), se usan las variables laborales del nivel urbano; mientras que se utiliza el programa X13-ARIMA-SEATS para ajustar la estacionalidad y quiebres estructurales en las series de tiempo (U. S. Census Bureau, 2017).
La Figura 1 muestra los métodos de interpolación que se usaron en las series de tiempo de la PEA, empleo, tasa de desempleo, empleo adecuado, porcentaje de empleo adecuado y salario nominal promedio.
En primera instancia, se observa que el ajuste por outliers identificados conserva los datos calculados por INEC con representatividad nacional y corrige los datos sin representatividad nacional para mantener la dinámica macroeconómica.
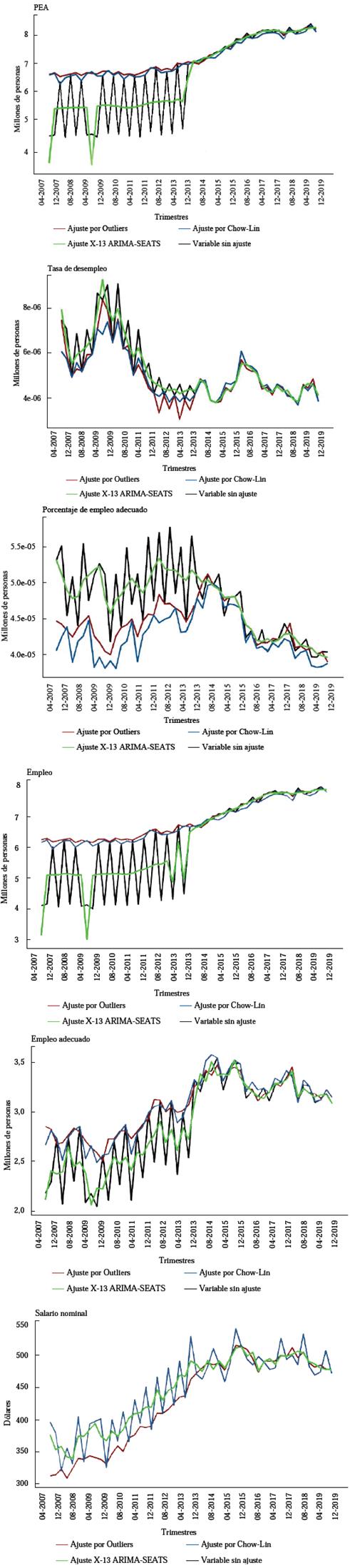
Fuente: INEC (2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019).
Figura 1 Variables del mercado laboral entre 2007 y 2019
La interpolación de Chow-Lin, de cierta manera, conserva también la dinámica agregada de las variables laborales. Al considerar el ajuste automático, se evidencia una reducción de las personas en la PEA, con empleo y con empleo adecuado, lo que genera quiebres estructurales que estadísticamente podrían ser concordantes, pero que no serían acordes con la realidad del mercado laboral y la información recolectada en la ENEMDU.
En el periodo 2007-2013, se evidencia un comportamiento estacional marcado en los meses de marzo y septiembre para todas las variables de interés en la ENE-MDU. El ajuste por outliers identificados o por Chow-Lin conserva esta propiedad de las series de tiempo en dicho periodo. Sin embargo, el ajuste automático no siempre produce una corrección adecuada, debido a la volatilidad y los valores atípicos en la serie. Las variables dummies específicas permiten eliminar esos cambios bruscos y la alta variabilidad ocasionada por la pérdida de representativi-dad en estos periodos.
En el caso de las poblaciones como la PEA, la empleada y la desempleada, el ajuste por outliers identificados elimina estas altas fluctuaciones, las cuales serían irreales si se comparan de un trimestre a otro, y nos permite corregir el nivel de representatividad, producto de la muestra de la ENEMDU en los meses de marzo y septiembre.
Por último, el método de ajuste automático del programa X13-ARIMA-SEATS permite hacer una corrección que conserva las fluctuaciones debidas a otros componentes en la serie; a diferencia del método de Chow y Lin (1971), donde se asume que la variable de análisis satisface una relación de regresión múltiple con sus indicadores auxiliares.
APLICACIÓN MACROECONÓMICA
En esta sección se presenta un ejercicio econométrico que permite evidenciar el uso de las variables laborales en los modelos macroeconómicos. En la primera parte, se presenta un modelo SVAR que, como proponen Blanchard y Quah (1989), involucra al PIB y a la tasa de desempleo para estimar el efecto de la demanda y la oferta agregadas en la economía.
Según estos autores, en el largo plazo los cambios inesperados de la demanda agregada no tienen un efecto en el PIB; mientras que los choques de oferta sí tienen efecto tanto en el corto como en el largo plazo. Para esto, estiman un modelo SVAR con restricción de largo plazo. En el caso ecuatoriano, inicialmente se estima la misma especificación; luego se extiende dicho modelo para incluir el empleo, el salario real y la inflación, como lo hacen Galí (1999) o Keating (2013).
Estas especificaciones permiten comparar el ajuste por outliers identificados de las variables temporales del mercado laboral que aquí se propone con la interpolación de Chow-Lin y de ajuste automático (X13-ARIMA-SEATS). Tanto en el modelo básico del producto y el desempleo como en el de las cinco variables, se incluyen la demanda internacional, el precio internacional del petróleo y dos dummies de la crisis de 2008 y 2014 para controlar los efectos que tiene el mercado internacional en la economía ecuatoriana.
Modelo
Formalmente, el modelo SVAR se expresa así:
Donde y t es el vector de variables endógenas (crecimiento del PIB y desempleo); A. es la matriz de parámetros estructurales en el rezago j = 0,..., p.; es el vector de variables determinísticas incluidas en el modelo (como la constante y las dummies para controlar datos atípicos, como la crisis financiera internacional de 2008 y el colapso del precio del petróleo en el último trimestre de 2014); y e t es el vector de choques estructurales (demanda y oferta agregadas) con distribución normal N(0,1).
Una de las principales dificultades que plantea un modelo SVAR es la identificación de los choques estructurales. Sin dicha identificación, el vector ε t de la ecuación (8) sería un vector de residuos estadísticos correlacionados que no tendrían una interpretación económica (Rubio-Ramírez et al., 2010). El modelo base desarrollado usa el enfoque de Blanchard y Quah (1989) para identificar las relaciones de largo plazo de las variables incluidas en el modelo con los choques de demanda y oferta. Los autores indican que, en un modelo con variables estacionarias, la ecuación (8) se puede expresar con la representación de la media móvil así:
Donde C es la matriz de efectos acumulativos de largo plazo de la demanda y oferta agregadas. En este sentido, Blanchard y Quah (1989) indican que los choques de demanda no tienen un impacto acumulado sobre el nivel del PIB, lo que indica que esta variable retorna a su estado de largo plazo ante cambios de la demanda agregada, de acuerdo con la teoría neokeynesiana. Por su parte, el choque de oferta sí tendría efecto en el PIB en el largo plazo. En este sentido, se impone la siguiente restricción sobre la matriz de efectos de largo plazo:
El modelo expuesto se estima a través de máxima verosimilitud (véanse Kilian y Lütkepohl, 2017). Para estimarlo, se incluyen las variables ajustadas, tanto por esta-cionalidad como por no representatividad nacional. Además, se incluyen la demanda internacional (medida como el PIB de Estados Unidos, Europa y China), el precio internacional del petróleo ( West Texas Intermediate, WTI) y dos variables dummies que controlan la crisis financiera del 2008 y la caída del precio internacional del petróleo como variables exógenas. Todas las variables se incluyen en tasas de crecimiento (primera diferencia del logaritmo), excepto la tasa de desempleo.
Resultados
Los resultados del modelo SVAR desarrollado siguiendo a Blanchard y Quah (1989) indican que los choques de demanda no tienen un impacto acumulativo en el PIB. En primera instancia, se presenta el efecto de los choques de oferta y demanda agregadas en el crecimiento del PIB y en la tasa de desempleo. Enseguida se presentan modificaciones del modelo básico para probar la concordancia de los resultados presentados.
La Figura 2 muestra el choque de demanda agregada en la tasa de crecimiento y en el desempleo, donde se comparan los métodos de interpolación. Se observa que los cambios inesperados de demanda agregada son temporales y tienen un efecto positivo en los próximos dos trimestres, para luego retornar a su estado inicial, tal como muestran Blanchard y Quah (1989). Este resultado en la función de impulso-respuesta se observa también en el ajuste por Chow-Lin y en el ajuste automático (X13-ARIMA-SEATS), debido a que estos métodos no introdujeron ningún ajuste en el PIB.
El efecto de la demanda agregada muestra una reducción de 0,2 puntos porcentuales en la tasa de desempleo con el método de ajustes por outliers. Este efecto tiene una duración de cinco trimestres después del choque.
En la estimación puntual, con el método de Chow-Lin, los cambios inesperados de la demanda agregada son ligeramente mayores con respecto al método aquí propuesto, aunque el mediano plazo es similar.
No obstante, con un ajuste automático por X13-ARIMA-SEATS, se tendría un impacto de 0,05 puntos porcentuales en la tasa de desempleo, menor al obtenido con el ajuste por outliers identificados. Además, este ajuste automático presenta una mayor persistencia en la respuesta del desempleo ante choques de demanda agregada. Ambas metodologías, sin embargo, muestran que no son diferentes (estadísticamente) del ajuste por outliers identificados (véase Figura 2).
Al analizar el choque de oferta, en la Figura 3 se observa que no existe un efecto en el crecimiento del PIB, tanto con el ajuste por outliers identificados como con los otros métodos, pues los intervalos de confianza contienen el cero.
Aunque parezca contradictorio con la literatura sobre choques de oferta, autores como Díaz-Cassou (2020) o Deza y Ruiz-Arranz (2018) muestran que la productividad total de los factores (una de las variables fundamentales de la oferta agregada) no contribuyó al crecimiento económico del país en los últimos años. Estos autores identifican que una de las principales razones es la dispersión de la productividad entre los sectores de las empresas y dentro de ellos mismos, acompañada de factores institucionales y regulatorios que afectan el clima de negocio en el largo plazo.

Nota. Los intervalos de confianza corresponden al modelo con las variables laborales que tienen el ajuste por outliers. Estos intervalos de confianza se generaron a través de 1000 repeticiones de bootstrap.
Figura 2 Efecto del choque de demanda agregada en el modelo básico

Nota. Los intervalos de confianza corresponden al modelo con las variables laborales que tienen el ajuste por outliers identificados. Estos intervalos de confianza se generaron a través de 1000 repeticiones de bootstrap.
Figura 3 Efecto del choque de oferta agregada en el modelo básico

Nota. Los intervalos de confianza corresponden al modelo con las variables laborales que tienen el ajuste por outliers identificados. Estos intervalos de confianza se generaron a través de 1000 repeticiones de bootstrap.
Figura 4 Choques de demanda y oferta agregadas en el modelo extendido
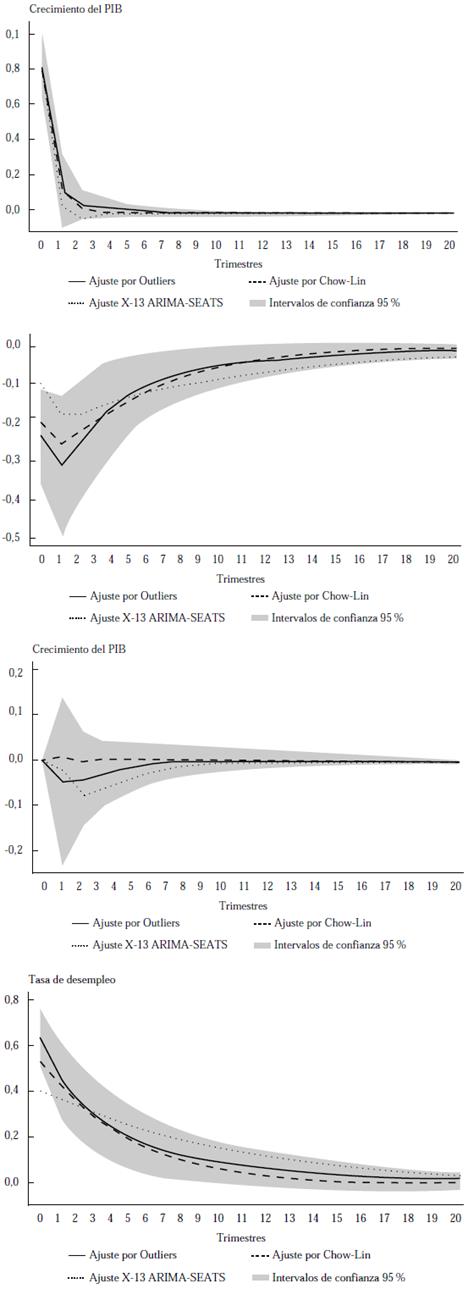
Nota. Los intervalos de confianza corresponden al modelo con las variables laborales que tienen el ajuste por outliers identificados. Estos intervalos de confianza se generaron a través de 1000 repeticiones de bootstrap.
Figura 5 Choques de demanda y oferta agregadas en el modelo extendido con la tasa de empleo adecuado
El mismo choque de oferta agregada provoca un incremento en la tasa de desempleo con efecto de mediano plazo. Estos cambios inesperados de la oferta tienen una duración de ocho trimestres (dos años). En la estimación puntual, se observa que el ajuste por outliers identificados y el de Chow-Lin muestran una dinámica similar en la respuesta del PIB ante el choque de oferta; mientras que el ajuste automático de X13-ARIMA-SEATS presenta un impacto menor a los otros métodos y un efecto (después del choque) con mayor persistencia.
Estos resultados muestran que las estimaciones concuerdan con las obtenidas por Blanchard y Quah (1989). En ese sentido, se puede sostener que la reconstrucción de la tasa de desempleo usando el método de ajuste por outliers identificados es concordante. Por consiguiente, el desempleo y las otras variables del mercado laboral permiten hacer ejercicios econométricos con datos trimestrales desde el 2007.
Para verificar la robustez de los resultados obtenidos se introdujeron modificaciones al modelo básico del crecimiento del PIB y de la tasa de desempleo.
En una primera modificación, se incluyeron el empleo, el salario real y la inflación en los modelos con las tres especificaciones, completando un modelo SVAR de cinco variables en cada tipo de interpolación. La incorporación de estas variables está en línea con Blanchard y Quah (1989), Dolado y Jimeno (1997) y Galí (1999).
En una segunda modificación, se reemplazó al empleo total por la tasa de empleo adecuado, debido a que no todos los trabajadores tienen las mismas condiciones laborales, siendo esta una característica estructural del mercado laboral ecuatoriano (véanse Arias et al., 2020).
Las Figuras 4 y 5 muestran los efectos de los choques de oferta y demanda agregada en la tasa de crecimiento y en la tasa de desempleo con el modelo SVAR de cinco variables. Los resultados muestran que se obtienen funciones de impulso-respuesta estadísticamente similares en todos los casos, tanto en magnitud como en persistencia. Además, se evidencia que, al incorporar empleo, inflación y salario real, se obtienen estimaciones puntuales sin mayor diferencia entre el método de Chow-Lin y el de ajuste de outliers identificados.
Una diferencia particular de la estimación de punto se observa en la respuesta del desempleo ante el choque de demanda agregada. En el modelo bivariado, se obtiene un efecto mayor con la metodología de Chow-Lin, mientras que la magnitud de la respuesta del desempleo ante cambios inesperados de la demanda es mayor con el ajuste de outliers identificados. Esta diferencia solamente se presenta en la estimación de punto, pues las estimaciones de los dos métodos son estadísticamente iguales.
Autores como Galí (1999) o Keating (2013) señalan que, en un modelo con más de dos variables, es necesario dar a los diferentes choques una interpretación económica. Esta interpretación siempre deberá estar atada a la teoría económica, tanto desde la oferta como desde la demanda agregadas. Así, se pueden entender choques de oferta como choques de tecnología, oferta laboral o capacidad de utilización. Para la demanda agregada, se pueden considerar, por ejemplo, choques de política económica (véase Galí, 2011).
CONCLUSIONES
En este trabajo, se desarrolló un método que permite usar los datos del mercado laboral extraídos de la ENEMDU que no tienen representatividad nacional, para así tener series de tiempo trimestrales continuas del mercado laboral ecuatoriano sin una ruptura desde 2007.
Este método parte, a su vez, del método de ajuste de outliers identificados e introduce variables dummies para los trimestres en los que la ENEMDU no tiene representatividad nacional. Para corroborar que los datos son empírica y macro-económicamente concordantes, se estimó un modelo SVAR de largo plazo con la propuesta de Blanchard y Quah (1989).
Los principales resultados muestran que el método propuesto conserva los valores obtenidos en los trimestres con representatividad nacional y ajusta solamente los valores no representativos. En contraste, si se usa un modelo automático de corrección de outliers (X13-ARIMA-SEATS), se introducen quiebres estructurales ficticios que cambian la dinámica de las variables del mercado laboral. Además, se observa que el método propuesto captura fluctuaciones que no lograrían capturar métodos de desagregación temporal como el de Chow y Lin (1971), que depende de variables auxiliares que modifican la fluctuación de las variables en análisis.
Asimismo, en el momento de implementar el modelo SVAR, se obtienen estimaciones similares a los de la literatura neokeynesiana. Se muestra que los choques de demanda agregada tienen efectos de corto plazo, tanto en el PIB como en la tasa de desempleo. Además, los cambios inesperados de la demanda agregada no tendrían un impacto de largo plazo en el PIB. Por su parte, se muestra que los choques de oferta no tienen impacto en el PIB en el corto ni en el largo plazo. Este resultado se podría interpretar como indicando que la productividad no ha contribuido en mayor medida al crecimiento económico de Ecuador (véanse Deza y Ruiz-Arranz, 2018; Díaz-Cassou, 2020).
Este trabajo contribuye a una línea de investigación del mercado laboral ecuatoriano que use datos de alta frecuencia (trimestrales, por lo menos) desde una perspectiva macroeconómica. En dicha línea, se podrían evaluar los factores determinantes de las variables del mercado laboral. Además, se podrían estudiar los diferentes canales de transmisión de la política económica a las variables laborales. Asimismo, se podrían identificar diferentes orígenes de los choques de oferta.