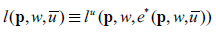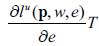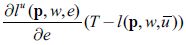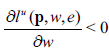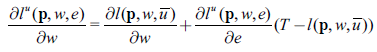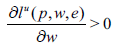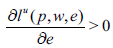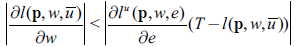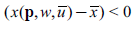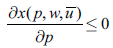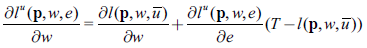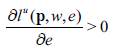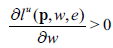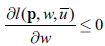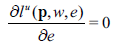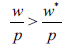It is common in economics to argue that all Giffen goods are inferior, but not all inferior goods are Giffen. In the past, goods such as potatoes and rice have been offered as -often questionable- examples of Giffen goods, when consumers have a lower income, and these examples have received some empirical support.
This article uses standard microeconomic theory, taking into account the initial endowments of goods and services, to prove propositions regarding the characteristics of Giffen goods in general, and leisure in particular. Leisure is shown to be a normal good, when it is Giffen. Thus, not all Giffen goods, are inferior goods. These findings suggest that leisure could be a Giffen and a normal good for consumers with a higher income, and these results could be useful for example, when finding empirical evidence on labour supply and in the design of policies in an era of machine learning and artificial intelligence.
Thus, this section is followed by a brief revision of the previous literature. Then, the standard theoretical framework is delineated and that is followed by some conclusions.
PREVIOUS LITERATURE
Giffen goods have been known since the 19th century. Gray (1815, ch. 5) described carefully the casual observation of Giffen goods in a book chapter entitled: "A rise in the price of bread corn, beyond a certain pitch, tends to increase the consumption of it".
Alfred Marshall (1985, p. 208), in the third edition of his Principles, acknowledged that the law of demand may not always work and described the Giffen paradox as follows:
There are however some exceptions [to the law of demand]. For instance, as Mr Giffen has pointed out, a rise in the price of bread makes so large a drain on the resources of the poorer labouring families and raises so much the marginal utility of money to them, that they are forced to curtail their consumption of meat and the more expensive farinaceous foods: and, bread being still the cheapest food which they can get and will take, they consume more, and not less of it. But such cases are rare; when they are met with they must be treated separately.
In general, the literature in economics has shown that the existence of Giffen goods is theoretically possible, and some empirical studies provide support to such possibility.
For example, Haagsma (2012) reviews the history of Giffen goods and a range of explanations for said occurrence, and states that the Giffen Paradox and the upward sloping demand curves, have kept many economists puzzled for more than a century.
Ashenfelter and Heckman (1974) decompose the income and the substitution effects to theoretically and empirically analyse a family's labour supply. They assume that leisure is a normal good, and their estimates support such assumption.
Jehle and Reny (2013, p. 56) in their theorem 1.13, state that "If an own price decrease causes a decrease in quantity demanded, the good must be inferior".Varian (2010, p. 144) points out that "a Giffen good must be an inferior good. But an inferior good is not necessarily a Giffen good". Nicholson (2005, p. 650) explains that the Giffen Paradox "arises because the good in question is inferior".Pindyck and Rubinfeld (2013, p. 122) state that a Giffen good is a good whose "demand curve slopes upward because the (negative) income effect is larger than the substitution effect". Von Mouche and Pijnappel (2012) explore weaker conditions in order to provide a strong form of the compensated law of demand, concluding that for an upper semi-continuous utility function, each Giffen good is inferior. This list does not pretend to be exhaustive, but aims to illustrate the point.
In fact, this is such a standard result in economics, that Stein (2009, p. 6) develops mnemonic methods for students to remember that "all Giffen goods are inferior goods, but not all inferior goods are Giffen goods".
Dwyer and Lindsay (1984) question the rationality behind the idea that potatoes were Giffen goods in the 1845-1849 famine in Ireland. They argue for example that in such circumstances, the supply of potatoes was lower and not greater than before; that the income effects from the supply side were confounded with income effects from the demand side; and that the analyses were being applied to what are in practice, closed economies in food.
Vandermeulen (1972, p. 458) studies the Giffen Paradox and concludes that a positive price effect is more likely with higher incomes than when living in poverty, and that the focus of economists on studying Giffen goods with lower incomes has given economists the "false assurance of the near infallibility of the law of demand".
Maskin and Tirole (1987) consider when sunspots can affect equilibria in a two-period, two-commodities, two-class economy, and find that in a non-degenerate imperfectly correlated equilibrium (one that is not a certainty equilibrium), leisure must be a Giffen good for at least one class of consumers. Furthermore, if the extrinsic signals received by consumers are independent, consumption must be a Giffen good for at least one class of consumers.
Larson and Johnston (1992a) and (1992b, p. 2) build a three good model with a money constraint and a time constraint, to argue that outdoor activities can be examples of Giffen goods. They point out as reasons as to why there has not been much evidence regarding Giffen goods in general -and outdoor activities as Giffen goods in particular-, the lack of knowledge concerning where and how to look for such evidence; model misspecification; omitted variables; a priori judgements; and "the strong self-selection against publishing such unusual results".
Battalio et al. (1991) employ experimental methods using rats, to confirm the existence of Giffen goods with strong inferiority, at the individual level.
More recently, Jensen and Miller (2008) found evidence that rice is a Giffen good for subsistence consumption in the Chinese provinces of Hunan and Gansu, and argue that this should be taken into account in the design of social policies.
Heijman and von Mouche (2012) provide a very thorough and complete collection of contemporary research on the subject, some of which is mentioned in this article, and argue that researchers are still trying to find answers to unknown aspects of Giffen goods.
In terms of policy, researchers from the International Labour Office, Ernst et al. (2019, p. 31) argue that artificial intelligence offers opportunities, such as a fall in the costs of capital and increases in productivity for low skilled workers, but also challenges, including a "continuous reduction in working hours, especially among those countries where long hours are still the norm, as well as sharing the receipts of innovation rents through profit sharing policies that have already been successfully implemented in some countries in the past".
This article proves propositons that aim to contribute to the previous literature on the subject, such as the literature that has been reviewed in this section.
THEORETICAL FRAMEWORK
In order to prove the propositions regarding leisure, a conventional theoretical framework is used, following for example, Angrist (2017) and Card (2016). Let:
• p be the vector of unit prices of goods and services
• p be the scalar of the unit price of the good or service being analysed
• w be the wage rate (unit price of labour)
• ū be a fixed level of utility
• e be the expenditure
• m be the non wage income
• y be the total income
• T be the total allocation of time
• h be the number of hours worked
• h(p, w, ū ) be the compensated (Hicksian) supply of labour
• l be the number of hours of leisure
• l U (p, w, y) be the uncompensated (Marshallian) demand for leisure
• l (p, w, U ) be the compensated (Hicksian) demand for leisure
• x U (p, w, y) be the uncompensated (Marshallian) demand for good or service x
• x(p, w, ū ) be the compensated (Hicksian) demand for good or service x
• x̅ be the endowment that a consumer has of good or service x
• e( p ,w, ū ) be the expenditure function
• e * (p, w, ū ) be the excess expenditure function
The consumer problem can be characterised with duality: the consumer maximises utility subject to the budget constraint, or the consumer minimizes the expenditure to achieve a certain level of utility. Assume that the utility function is monotonic and strongly pseudoconcave locally and thus, that the demand functions are locally differentiable1, and that the time endowment is allocated between work and leisure only. The results presented here hold, as long as the demand functions are locally differentiable. Deviations from this assumption are considered as special cases in some parts of the article, and the extreme and unlikely cases of the perfect substitutes and Leontief preferences, where the compensated demand of leisure is vertical or has vertical and horizontal segments, are analysed at the end of the article.
The budget constraint can be written as:
The expenditure function, that is, the minimum expenditure required to reach a level of utility U with a given vector of prices (p, w), can be written as:
The compensated demand of leisure can be obtained by Shephard's Lemma:
Because of the concavity of the expenditure function:
Since it has been assumed that time can only be used for leisure or labour, the expenditure function can also be written as:
Following Angrist (2017), the excess expenditure function, that is, the non-wage income that a person requires to get to the level of utility U with a given vector of prices (p, w), can be written as:
By Shephard's Lemma, as a direct application of the envelope theorem:
A useful identity is:
Deriving this identity with respect to the wage rate:
Replacing equation 3 on equation 5:
Solving for the change in the uncompensated demand of leisure, yields the Slutsky equation with endowment effects:
Which can be written as:
This is the same equation as the one presented in Varian (1992, p. 146). Here, the impact of a change in the wage rate on the uncompensated demand for leisure, can be decomposed into a substitution effect:
An endowment effect:
And an income effect:
For the benefit of brevity, the endowment effect and the income effect shall be combined and referred to here, as the net income effect, as follows:
If as pointed out in equation 2:
And assuming that there is always an interior solution, so:
and:
The following propositions regarding leisure hold:
Proposition 2.1. If leisure is inferior, it has to be ordinary.
Proof.
If:
Then:
Proposition 2.2. If the income effect is zero, leisure has to be ordinary.
Proof.
If:
Then:
Proposition 2.3. If leisure is normal, it can be ordinary.
Proof.
If:
And:
Then:
Proposition 2.4. If leisure is perfectly inelastic to the wage rate, it has to be normal.
Proof.
If:
Then
And furthermore:
Proposition 2.5. If leisure is Giffen, it has to be normal.
Proof.
If:
Then
And furthermore:
The above propositions can be represented graphically, as shown in figure 1.
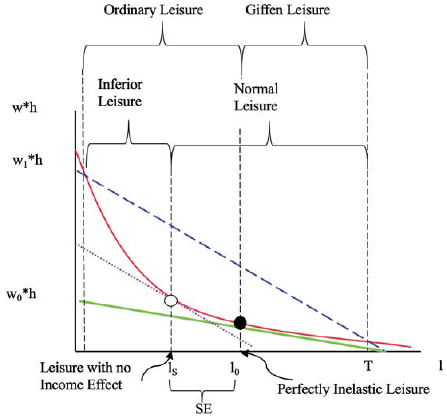
Source: Author.
Figure 1 Graphic Representation of Leisure as Different Types of Goods, Depending on Consumer Preferences
From an initial optimal bundle depicted by the black circle on the green continuous budget line in figure 1, when the wage rate increases from w0 to w1, the value of time increases, and the new budget line is the blue dashed line. The type of good leisure is, depends on the preferences of the individual. When the consumer optimises, such optimal decision should be on the new dashed blue budget line, somewhere between the two black vertical dotted lines on the extremes of the graph (where the initial welfare intersects the new blue budget line). All the propositions proved so far in this article, hold in this graph.
Leisure is a special kind of good, in the sense that for all consumers, its demand is always lower or equal to the endowment of time, that is, its excess demand -optimal demand of leisure minus the endowment of time is always non-positive. The following proposition looks into the general case, including the case of more conventional goods and services, in which the excess demand can be positive, zero or negative, but is usually positive.
Proposition 2.6. A Giffen good is an inferior good if its excess demand is positive, and a normal good if its excess demand is negative.
Proof. The Slutsky equation with endowment effects, -as presented in Varian (1992, p. 145)-, is given by:
If:
And the excess demand of the good is positive:
And allowing for extreme cases:
Then:
And:
If:
And the excess demand of the good is negative:
And allowing for extreme cases:
Then:
And:
Note that the case of leisure, is a special case of proposition 2.6. Since the excess demand of leisure is assumed to be negative, if leisure is Giffen, it has to be a normal good.
Consider now the theoretically possible, but extreme and unlikely case of Leontief preferences, between leisure and the consumption of all other goods.
Proposition 2.7. If the consumption of leisure and all other goods can be described with Leontief preferences, leisure has to be a normal and a Giffen good.
Proof.
In the Leontief preferences case, the partial derivative of leisure demand with respect to the wage rate is not defined, but the substitution effect is zero for positive wages.
The income effect has to be positive because the indifference curves cannot intersect:
And since it has been assumed that:
Then:
This extreme case is described in figure 2.
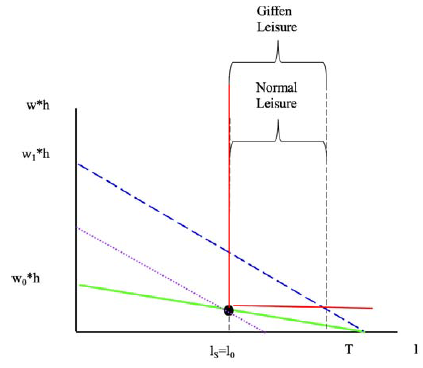
Source: Author.
Figure 2 Graphic Representation of Leisure as Different Types of Goods, with Leontief Preferences
In figure 2, an increase in the wage rate from w 0 to w 1 will lead to a new optimum on the new dashed blue budget line, strictly in between the original red indifference curve.
Consider now as well the theoretically possible, but also extreme and unlikely case, of preferences in which leisure and consumption of all other goods, are perfect substitutes.
Proposition 2.8. If the consumption of leisure and all other goods are perfect substitutes, leisure has no income effect and leisure is not Giffen.
Proof.
Let the slope of the indifference curves be:
If
The demand for leisure is undetermined and in the range:
If the wage rate changes (increases or decreases), a corner solution is obtained: The substitution effect is non-positive:
And the income effect on leisure is zero:
Thus:
If:
Or
There is a corner solution.
In this case, for changes in prices that maintain the same corner solution: The substitution effect is zero:
And the income effect on leisure is zero.
And for changes in prices that lead to a change in the consumption of leisure, including a change of the corner solution:
The substitution effect is non-positive:
And the income effect on leisure is zero.
Thus, when leisure is a perfect substitute for the consumption of other goods, leisure has no income effect and leisure cannot be a Giffen good.
This case is depicted in figure 3.
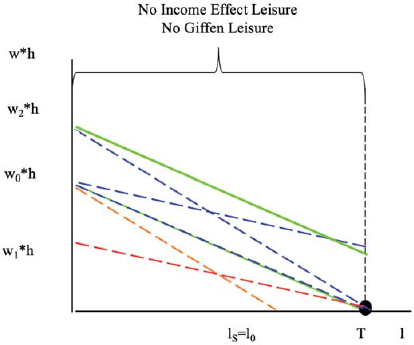
Source: Author.
Figure 3 Graphic Representation of Leisure as Different Types of Goods, when Leisure and all Other Goods are Perfect Substitutes
In figure 3, preferences are in green and the budget lines are dashed blue. Assume to start with, that the budget constraint and the indifference curve overlap. In this case, the optimal bundle is undetermined between 0 and T, and any change in the relative prices leads to a corner solution. The budget lines that keep the initial level of utility constant for a given change in relative prices and thus, allow to identify the substitution effects, are in red. Given a corner solution, any change in the relative prices that leads to the same corner solution -or another corner solution-, has a non-positive substitution effect, and has no income effect on the demand for leisure.
The demand curve for leisure in this case, is shown in figure 4.
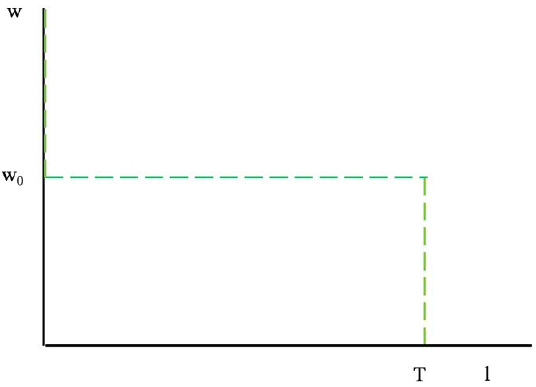
Source: Author.
Figure 4 Graphic Representation of the Demand for Leisure when Leisure and all Other Goods are Perfect Substitutes
Note that the special cases described in propositions 2.7 and 2.8, do not change the main results obtained in previous propositions.
Overall, it is possible to conclude that when the endowments of goods and services are taken into account, if any good or service is Giffen, then it must be inferior if its excess demand is positive, and it must be normal, if its excess demand is negative. Leisure is a special type of good and service, since it is characterised by having a non-positive excess demand: its optimal demand is always less or equal to the endowment of time. Thus, if leisure is a Giffen good, it has to be a normal good. But not all normal leisure, is a Giffen leisure.
Note as well that the results provided in this article can be useful when finding empirical evidence regarding labour supply, and for understanding the impacts of machine learning and artificial intelligence on the labour market, and the impact of policies to address some of those challenges. For example in terms of hours worked due to changes in hourly wages, or income transfers, as has been highlighted by researchers from the International Labour Office.
CONCLUSIONS
It is well known in the economic literature, that the labour supply curve can bend backwards, and thus, that leisure can be a Giffen good. It is also known that leisure can be a normal good. This article has proved that if leisure is a Giffen good, it has to be a normal good. This result proves as well that, contrary to common knowledge in economics, once the initial endowments are taken into account, not all Giffen goods, are inferior goods.
Additionally, this article shows, within the standard microeconomics literature, that if leisure:
Is inferior, it has to be ordinary
Has no income effect, it has to be ordinary
Is normal, it can be ordinary
Is perfectly inelastic to the wage rate, it has to be normal
Is a perfect complement of all other goods, the demand for leisure is Giffen and normal
Is a perfect substitute for the consumption of all other goods, leisure has no income effect and leisure is not Giffen
Thus, if leisure is a Giffen good, it has to be a normal good, but not all normal leisure, is a Giffen leisure.
In general, it has been proved that if any good or service is Giffen, then it must be inferior if its excess demand is positive, and it must be normal if its excess demand is negative. The results presented in this article depart from the standard economic literature, because they take into account the endowment effects of the changes in the prices of goods and services.
In the past, potatoes and rice have been used as examples of Giffen goods for lower income consumers, and there is some empirical evidence to support this. In the future, leisure may be used more frequently as an example of a Giffen and a normal good for higher income consumers, and this could be taken into account for example, when finding empirical evidence on leisure and labour supply, and when designing policies in an era of machine learning and artificial intelligence. More generally, goods and services with endowments that are greater than their optimal demands, may also turn out to be good examples of Giffen goods.