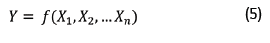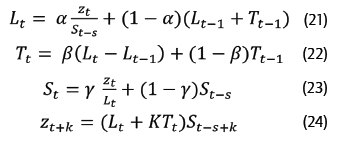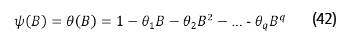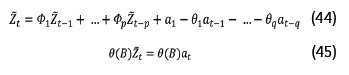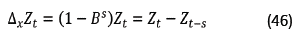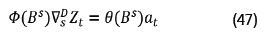Introdução
As empresas necessitam planejar as suas operações com relação à oferta de produtos ou de serviços. A previsão de demanda é uma metodologia da administração de empresas para estimar um valor futuro de uma grandeza de interesse. As previsões são elemento necessário no processo de tomada de decisão sobre o futuro (Petropoulos et al, 2018). Realizar previsões de demanda significa reconhecer padrões de comportamento em séries históricas e predizer o comportamento futuro ou, ainda, identificar fatores causais que afetam o comportamento e extrapolá-lo.
Existem métodos de previsão de demanda basicamente classificados em quantitativos e qualitativos (Arvan et al., 2019), aplicados ao consumo e à produção de bens ou de serviços. Método, em seu conceito fundamental, caracteriza-se pela coleta e pela organização de informações e sua devida interpretação segundo um princípio, a fim de explicar ou prever determinados eventos. Modelo é uma idealização reduzida de um sistema que apresenta maior complexidade, mas que reproduz, na sua essência, a parte que interessa do comportamento do sistema complexo. Métodos quantitativos geralmente não necessitam de julgamento, pois são procedimentos padronizados que produzem resultados objetivos por meio de modelos matemáticos. Já os métodos qualitativos não requerem manipulação de dados, e somente julgamentos são utilizados para criar a previsão (Jun et al, 2017).
Nos anos 1970, George Box e Gwilym Jenkins propuseram os métodos autorregressivos integrados à média móvel (Arima, na sigla em inglês). Os autores basearam seus estudos na premissa que valores em sequência de uma série temporal sejam mutuamente dependentes, e essa dependência seja alta (Brentan et al, 2017). Com o advento da computação, passou-se a utilizar métodos baseados em computação e fundamentados em modelos com inteligência artificial que modelam situações simples e complexas, e apresentam a capacidade de identificar relacionamentos não lineares e interativos (Wang et al., 2018). Já a partir de 2010, as redes neurais artificiais e as abordagens compostas, como neuro-fuzzy e associados aos modelos caóticos, foram consideradas uma poderosa ferramenta computacional para resolver problemas complexos em previsão de demanda (Fiot & Dinuzzo, 2016; Tapia Cortez, Hitch et al., 2018).
Sob o aspecto acadêmico, pesquisas como a de Raza e Khosravi (2015) trazem uma revisão sobre técnicas de previsão de demanda de carga baseada em inteligência artificial para redes e edifícios inteligentes. Deb et al. (2017) apresentam uma revisão sobre as técnicas de previsão com uso de séries temporais voltadas ao consumo de energia. Katsikopoulos et al. (2018) revisaram e sintetizaram pesquisas que usaram análises matemáticas e simulações em computador em modelos simples e complexos. Armstrong e Green (2019) discorreram sobre os diferentes métodos de previsão de demanda em aplicações empíricas.
O uso do julgamento humano, único ou em conjunto com modelos quantitativos, foi amplamente pesquisado na literatura acadêmica e é uma abordagem popular de previsão na prática da administração de empresas. Arvan et al. (2019) apresentam uma revisão sistemática da literatura sobre previsão de demanda julgadora, com foco na integração de métodos. Entretanto, percebeu-se a lacuna de uma pesquisa acadêmica que faça a revisão da literatura que contemple os métodos qualitativos, quantitativos e com base em inteligência artificial, com o foco voltado à administração de empresas, no que diz respeito ao consumo e à produção de produtos e serviços.
Sob o aspecto empresarial e social, o tema da previsão de demanda indica ser atual e relevante para as instituições de diversos segmentos de atuação. As consequências de um plano de trabalho inadequado são inúmeras e prontamente percebidas (Arvan et al., 2019). Como consequência, pode afetar a qualidade, a satisfação do cliente e o custo, e prejudicar a eficiência operacional do negócio (Tratar, 2015); em consequência, pode gerar impactos negativos tanto para as organizações quanto para a sociedade.
Assim, conhecer os conceitos, os métodos e os modelos para prever a demanda de produtos, serviços, materiais e otimizar a utilização dos recursos organizacionais tornam-se relevantes para a comunidade acadêmica no campo teórico da administração de empresas. Também se torna relevante para as empresas no que se refere à gestão de recursos e para a sociedade como geração de progresso económico e financeiro. Nesse sentido, a questão de pesquisa que este artigo enfocou foi: quais são os métodos de previsão de demanda sobre o consumo e a produção de produtos e serviços utilizados atualmente na administração de empresas?
O objetivo deste estudo é, portanto, realizar uma revisão da literatura dos métodos de previsão de demanda com o propósito de reunir os métodos e modelos disponíveis acerca dos conceitos utilizados atualmente na administração de empresas relacionados ao consumo e à produção de produtos e serviços. O artigo está separado em quatro seções. Após a introdução ao tema de pesquisa, na seção de metodologia, são descritas a abordagem e a metodologia de estudo. Na terceira seção, encontra-se a revisão da literatura que descreve os métodos de previsão de demanda, tratados em termos de métodos qualitativos, métodos quantitativos e métodos com base em inteligência artificial. As conclusões, as considerações finais e as sugestões de novos estudos são apresentadas na última seção.
Metodologia
A metodologia utilizada neste artigo é a revisão da literatura com abordagem qualitativa e com o propósito de dar uma visão descritiva geral dos métodos dominantes utilizados em previsão de demanda (Wee & Banister, 2016). Foi realizado o mapeamento da literatura para identificar o estado da ciência por meio da produção científica disponível nos bancos de dados mais relevantes (Zupic & C ater, 2015). A pesquisa foi conduzida em quatro etapas: i) definição dos termos de busca, ii) pesquisa nas bases de dados, iii) coleta e avaliação dos artigos e iv) interpretação dos resultados.
Na primeira etapa, foram definidos os termos de busca "demand forecasting", "demand forecasting methods" e "demand forecasting models". Os termos de busca foram utilizados na língua inglesa presentes no título, no resumo ou nas palavras-chave. As pesquisas dos termos de busca, ou seja, a etapa dois, foi realizada nos bancos de dados Scopus e Google Scholar. Ambos os bancos de dados foram selecionados por apresentarem o maior número de artigos relacionados aos termos de busca. As buscas foram refinadas, restringindo-as somente a documentos do tipo "artigo", em língua inglesa, de 2015 a 2020, para se ter uma base atual de pesquisa (Zupic & Cater, 2015). A tabela 1 mostra as quantidades de artigos por base de dados ao final da etapa dois.
Tabela 1 Termos de busca utilizados
| Termos de busca | Base de dados | |
|---|---|---|
| Scopus | Google Scholar | |
| Quantidade de resultados | ||
| "demand forecasting" | 5.105 | 17.400 |
| "demand forecasting methods" | 141 | 673 |
| "demand forecasting models" | 433 | 1.150 |
Fonte: elaboração própria.
Na terceira etapa, os arquivos foram analisados por título e resumo, para que fossem incluídos somente os documentos que se referem ao tema de pesquisa e selecio-nados por ordem de documentos mais citados. Do total de 22.505 artigos, foram excluídos 22.454 pelo título e pelo resumo, bem como arquivos duplicados, o que resultou 51 para as análises. A etapa quatro foi a análise sobre os diferentes métodos de previsão de demanda e os seus conceitos, o que permitiu, em pesquisa acadêmico-descritiva única, reunir os métodos e os modelos disponíveis acerca dos conceitos utilizados atualmente na administração de empresas relacionados ao consumo e à produção de produtos e serviços.
Revisão da literatura
As previsões de demanda desempenham um importante papel em diversas áreas na gestão de organizações e, independentemente do tamanho ou da área de atuação, todas as empresas necessitam planejar. Planos de negócios, geralmente, confiam e necessitam de alguma forma de previsão de demanda, principalmente da previsão de variáveis relacionadas a elementos de produção, tais como capacidade, matérias-primas, mão de obra e capitais de giro (Petropoulos et al, 2018). Previsões são usadas extensivamente nos negócios para planejamento e gerenciamento tático, estratégico ou operacional em horizontes diferentes que variam de dias, semanas ou meses, embora o nível de detalhamento seja diferente (Aboagye-Sarfo et al, 2015).
Nesse sentido, existe uma base comum e importante a todos os planejamentos que é a previsão de demanda. As previsões de demanda abrangem o grau de disponibilidade do produto na cadeia de suprimentos e caracterizam-se necessárias como elemento qualificador para uma melhor tomada de decisão com relação ao futuro (Fortsch & Kha-palova, 2016).
A necessidade de planejar surge do requisito de se trabalhar no presente em atividades que serão requisitadas como demanda futura. Porém, a realidade das organizações não é estática. A dinâmica de mudanças dos negócios em alguns casos pode ser gradual, em outros, podem ser súbitas (Ferreira et al., 2016). Os mercados também estão expostos a condições semelhantes. Um produto pode ter demanda constante por anos, enquanto outro produto pode desaparecer antes mesmo da fase do desenvolvimento do projeto ser finalizada. Serviços podem apresentar alta demanda em um período, ter baixa procura em outro período e ser substituídos por outros serviços inéditos na sequência.
As técnicas de previsões permitem transformações das informações empresariais estratégicas para prever a demanda por novos produtos, novas tecnologias, novas participações de mercado ou melhor estratégia competitiva. Afinal, as empresas necessitam planejar as suas operações e vendas de seus produtos ou serviços no futuro (Sellitto et al., 2017). Essa expectativa de desempenho pode ser usada como ponto de partida ou ancoragem para o conjunto de decisões a serem tomadas pelo corpo gerencial da empresa.
Entender a demanda por um produto ou serviço é um processo complexo e envolve elucidar relações existentes entre diversos fatores ou variáveis independentes. Compreender a influência das principais variáveis independentes na variável dependente e eventuais interações entre variáveis é necessário para construir um modelo que possa estimar, dentro de intervalos de confiança aceitáveis, uma variável representativa da demanda futura em um dado período. Para tanto, é necessário entender efeitos e influências ativas nos mecanismos de competição impostos ao mercado, o que usualmente não é uma tarefa simples. Alguns dos fenómenos envolvidos dependem de fatores económicos e de múltiplas alternativas de fornecimento, tanto de matéria-prima como de subsistemas intermediários necessários ao produto ou serviço final. Desse modo, é possível desenvolver métodos para identificar os principais fatores geradores de demanda e, ao mesmo tempo, lançar mão de métodos estatísticos para se chegar a modelos capazes de oferecer previsões úteis (Green & Armstrong, 2015).
Por meio da previsão de demanda, é possível reunir informações sobre quantidades das vendas ou requisições futuras de um item ou serviço ou ainda relacionadas ao consumo de um conjunto correlato de itens, tais como as partes constituintes de um produto industrial (Mancuzo, 2003). Algumas características são comuns entre os métodos de previsão. Umas dessas características é a perenidade ou a continuidade de causas que redundem na decisão de consumo de um produto ou serviço. Em síntese, métodos de previsão de demanda consideram que causas que ocorreram no passado e que determinaram uma decisão de consumo continuaram a atuar no momento futuro de interesse do estudo. Também é possível reconhecer padrões de comportamento em séries históricas e predizer o comportamento futuro. Outro modo é identificar fatores causais que afetam o comportamento e extrapolá-lo, segundo um modelo matemático (Arvan et al, 2019).
Uma característica comum a todos os métodos de previsão são os erros causados por fatores aleatórios, que impedem que se alcancem resultados perfeitos em previsões (Syntetos et al, 2015). Quanto maior o horizonte de previsão, maior será a chance de erro no futuro. Conhecer se a demanda por produtos ou serviços está aumentando ou diminuindo não é suficiente. O fluxo de informações, conhecimento, produto ou recursos entre essas entidades deve ser gerenciado adequadamente para maximizar a lu-cratividade geral e conhecer a taxa de mudança é fundamental no planejamento do negócio (Tapia Cortez, Hitch et al., 2018).
Os métodos de previsão de demanda basicamente são classificados em qualitativos e quantitativos (Arvan et al., 2019). Métodos qualitativos não requerem manipulação de dados e somente julgamentos são utilizados para criar a previsão, já os métodos quantitativos não requerem julgamento, sendo procedimentos padronizados que produzem resultados objetivos.
Métodos qualitativos
Os métodos de previsão de demanda qualitativos, também chamados "métodos baseados no julgamento", são fundamentados na capacidade de julgamento, de discernimento e na experiência de decisores especialistas (Petropoulos et al., 2018). Tais métodos são apropriados para criar cenários futuros quando há baixa disponibilidade de dados (Seifert et al, 2015), quando estes apresentam baixa contabilidade, quando se deseja estimar variáveis ligadas a produtos ou processos novos ou disruptivos (Arvan et al, 2019).
Julgamento por especialistas
Um dos métodos qualitativos de previsão de demanda é o julgamento por especialistas, também chamado "abordagem de painel", que tem como base utilizar a opinião e a experiência de especialistas para criar a predição de demanda (Armstrong & Green, 2019; Arvan et al, 2019). Os especialistas realizam individualmente a previsão e depois as partes são combinadas para se chegar à previsão agregada. As previsões são de longo prazo, envolvendo aspectos do planejamento estratégico da empresa.
A autoalavancagem por julgamento permite que dados preditos por especialistas sejam utilizados em modelos matemáticos, fazendo com que julgamentos subjetivos sirvam como base de informação em procedimentos estruturados. Para tanto, são inicialmente identificadas as informações utilizadas pelos especialistas na predição de demandas e, então, os especialistas elaboram previsões para diversos casos, reais ou hipotéticos (Arvan et al., 2019). Os dados resultantes são convertidos para um modelo que estima uma regressão em função do conjunto de previsões cole-tadas (Seifert et al, 2015).
Delphi
O método Delphi emprega um questionário que é enviado a especialistas, cujas respostas são analisadas, resumidas e retornadas anonimamente aos respondentes (Nikolopoulos et al, 2015). Segundo de Löe et al. (2016), a técnica Delphi foi desenvolvida na década de 1950 para estruturar a comunicação em grupo e a interação entre painéis de especialistas, com o objetivo de prever a ocorrência de eventos ou tendências por meio de processos iterativos.
Normalmente, é composto de uma equipe de cinco a 20 especialistas. Anonimamente, os especialistas respondem a formulários em que emitem e justificam suas previsões. O processo é repetido até que haja pouca alteração nas previsões entre as rodadas (von Briel, 2018). Duas ou três rodadas geralmente são suficientes, e o resultado da previsão será a mediana ou a moda das previsões finais dos especialistas (Arvan et al, 2019). De acordo com Kudlak et al. (2018), o método Delphi é frequentemente aplicado a fenómenos complexos e subexplorados na previsão de ciência e tecnologia, na previsão de negócios e na elaboração de políticas participativas.
Método de analogia estruturada
O método de analogia estruturada utiliza como referência os comportamentos passados com a finalidade de ajudar a prever o resultado de uma nova situação, por meio de analogias. Conforme Jun et al. (2017), é uma tentativa consciente e deliberada de aproveitar a experiência histórica, envolvendo uma comparação sistemática de algo a ser previsto com elementos anteriores que se acredita ter sido semelhante em todos ou em aspectos mais importantes.
No método de analogia estruturada, um administrador prepara uma descrição da situação objetivo e seleciona especialistas que conheçam situações análogas, preferencialmente que possuam experiência direta (Jun et al, 2017). Assim, os especialistas identificam e descrevem situações similares, classificam sua semelhança com a situação-alvo e combinam os resultados de suas analogias com resultados potenciais dessa situação-alvo. Desse modo, o administrador forma uma analogia de cada especialista com a mais semelhante aos demais especialistas, obtendo uma previsão análoga por especialista (Armstrong & Green, 2019).
Pesquisa de intenção e opinião
As pesquisas de intenção e opinião são utilizadas para verificar as intenções de compra ou padrões de comportamento referentes a determinadas condições. Nesse método, devem ser consideradas surveys que apresentem significância estatística para as generalizações (Armstrong & Green, 2019). Porém, por vezes, são usados grupos focados para esse fim, entretanto, nesse caso, não se trata de uma amostra significativa da população. As análises conjuntas também fazem parte desse grupo quando a pesquisa é realizada com a intenção de perceber os atributos que levariam a uma opção de compra ou um padrão de comportamento (Jun et al, 2017).
Métodos quantitativos
Os métodos de previsão de demanda quantitativos, também conhecidos como "métodos matemáticos", utilizam modelos matemáticos para se chegar aos valores previstos (Ren et al., 2016). Os métodos matemáticos permitem controlar o erro e são divididos em métodos causais e séries temporais.
Modelos causais
Nos modelos causais, demandas por produtos finais, produtos relacionados ou serviços, as chamadas "variáveis dependentes", apresentam relação causa-efeito com variáveis antecessoras, as quais, por sua vez, são chamadas "variáveis independentes" ou "causais". A demanda por um produto poderia ser prevista por meio de uma função de variáveis como preço, país de origem e assim por diante (Katsikopoulos et al, 2018). No método causal, a previsão de demanda é altamente correlacionada com certos fa-tores no ambiente, como fatores da economia e da taxa de juros de um país. Nos modelos causais, os dados seguem um comportamento identificável ao longo do tempo e existem relações identificáveis entre as informações que se deseja prever e outros fatores (Arvan et al, 2019).
Um modelo de regressão é um relacionamento entre o que se pretende prever, denominado "variável dependente" (y), e os fatores que determinam o valor de y denominados "variáveis independentes" (xi) (Katsikopoulos et al, 2018). O modelo de regressão simples analisa a relação entre duas variáveis, em que os dados apropriados para esse método consistem em observações, cada uma delas com duas medidas diferentes (Green & Armstrong, 2015). A regressão é significativa quando a variável dependente se relacionar de modo significativo com as variáveis independentes (Fang & Lahdelma, 2016). A regressão simples pode ser representada pela equação (1), ou seja, y é uma função de x:
em que:
y = variável dependente (demanda);
x = variável independente ou variável causal.
Quando a variável dependente está ligada exclusivamente a uma variável independente, existem diferentes possibilidades para sua função, entre os formatos mais utilizados estão:
em que:
a e b = representam valores numéricos constantes (parâmetros).
A equação (2) é uma regressão linear simples que assume o formato de uma reta. A equação (3) contém uma regressão exponencial. Já a equação (4) é uma regressão parabólica.
O modelo de regressão múltipla pode ser expresso pela função exposta na equação (5).
em que:
X 1 , X 2 ,... Xn = conjunto de n variáveis independentes.
Na regressão múltipla, existem variadas possibilidades de formato da função e do número de variáveis independentes a se considerar. Porém, é amplamente utilizada a regressão linear múltipla, representada na equação (6) (Wang et al., 2018). Esta regressão chama-se "linear", porque todas as variáveis independentes apresentam expoente igual a um.
em que:
b 0 , b 1 , b 2 ,... b n = são os parâmetros.
São apresentados diferentes métodos na literatura para resolver problemas não lineares. Para regressão simples não linear com a utilização da função exponencial, é possível aplicar a equação (7):
Por meio da função parabólica, o cálculo da regressão ocorre pelas equações (8), (9) e (10).
O método de Gauss-Newton ou da linearização expande o modelo não linear em uma série de Taylor aproximando-o por um modelo linear. No método de Gauss-Newton, a soma dos quadrados dos erros é reduzida ao pressupor que a função de mínimos quadrados é localmente quadrática e busca encontrar o mínimo da potência quadrática (Lv et al., 2017). Outro método é o método de Levenberg-Marquardt que, conforme Chae et al. (2016), é uma combinação de dois métodos de minimização: o método do gradiente descendente e o método de Gauss-Newton. Para o método do gradiente descendente, a soma dos quadrados dos erros é reduzida atualizando os parâmetros no sentido da maior redução dos mínimos quadrados objetivos. O método de Levenberg-Marquardt está mais para o método de gradiente descendente quando os parâmetros estão longe de seu valor ideal. Por sua vez, quando está mais próximo da convergência, o método Levenberg-Marquardt comportase como o método de Gauss-Newton (Shaikh & Ji, 2016).
Conforme Wang et al. (2018) e Deb et al. (2017), os resultados da regressão não linear são representativos se 1) o modelo possui justificativa, pois a regressão apenas ajusta parâmetros da equação escolhida; 2) os erros são normais, possuem variância constante, são independentes em relação a y e não correlacionados entre si; 3) a imprecisão na medição de y é pequena perante sua variabilidade; 4) o resultado apresentado faz sentido científico; e 5) às estatísticas obtidas são aceitáveis.
Séries temporais
A modelagem de séries temporais, também chamada "modelagem univariada", geralmente usa o tempo como uma variável de entrada sem outras variáveis explicativas externas. É definida como um conjunto de observações geradas sequencialmente no tempo (Boroojeni et al, 2017). A análise de séries temporais examina o padrão de comportamento passado de um fenómeno ao longo do tempo para prever o comportamento futuro (Villani et al, 2017). O método requer que se conheçam valores e comportamento pregressos da variável dependente, ou seja, da demanda. O conjunto de dados constitui um processo estocástico. Caso a variância se mantenha ao longo do tempo, o processo é dito estacionário; do contrário, é dito não estacionário (Fortsch & Khapalova, 2016). Esses métodos são utilizados para previsões de curto prazo quando os valores das observações seguem um padrão de comportamento identificável ao longo do tempo (Zhu et al, 2015).
Em métodos quantitativos por séries temporais, esperase que o padrão observado no passado se mantenha no futuro. Nesses métodos, o padrão conhecido fornece meios para a previsão de demandas desconhecidas, ou seja, demandas futuras. É possível decompor séries em quatro componentes (Deb et al, 2017; Tratar et al, 2016), também chamados "padrões de demanda", comportamentos ou efeitos associados a série temporal (Mancuzo, 2003; Stúker, 2014), conforme descrito a seguir.
Horizontal ou variações irregulares: são variáveis decorrentes de causas não identificadas de curto prazo, podendo ser imediatas. Apresentam natureza aleatória e não podem ser previstas por modelos estocásticos de previsão.
Efeito de tendência: faz com que a demanda possua uma tendência crescente ou decrescente com o tempo. Pode acontecer de a demanda apresentar-se estacionária, permanecendo próxima ou oscilando ao redor de um valor médio constante.
Efeito sazonal: casos em que a demanda de determinados produtos apresenta desempenho muito próximos em épocas específicas do ano.
Ciclo de negócios: são flutuações de ordem geral e de periodicidade variável, resultantes de diversas e diferentes causas. Possuem difícil previsão e são percebidas em economias capitalistas modernas.
As variações de uma série temporal que não possuam interpretação e explicações por meio dos quatro componentes citado anteriormente são decorrentes de ruído aleatório no processo gerador dos dados (Tratar et al., 2016). Entretanto, esse ruído não é matematicamente modelável, porém pode ser tratado ou seu efeito atenuado por filtros, entre eles, pode-se citar o filtro de Kalman.
Modelos de decomposição são séries em que há presença simultânea, de variações irregulares ou aleatórias, tendência, sazonalidade e ciclos de negócios. Essa decomposição permite isolar componentes, de tal modo que os efeitos possam ser tratados individualmente, com exceção feita a flutuações irregulares.
A combinação dos componentes em uma série é separada fundamentalmente em modelo aditivo e modelo multiplicativo (Afilal et al, 2016; Fortsch & Khapalova, 2016). O modelo aditivo aborda a série por meio da composição da soma dos componentes, conforme a equação (11).
em que:
y = valor da série ou demanda prevista;
T = componente tendencial;
S = componente sazonal;
C = componente cíclico;
i = efeitos aleatórios ou erros causados por flutuação.
Para as quantidades de T, S, C, i, os valores são representados em unidades de demanda somados.
O modelo multiplicativo, bastante utilizado, é expresso pela equação (12) (Fortsch & Khapalova, 2016).
em que os componentes têm os significados já expostos.
No modelo multiplicativo, a tendência é expressa em unidades de demanda e as demais quantidades são representadas em porcentagens da tendência. O modelo multiplicativo pode ser simplificado caso seja possível que o horizonte de previsão seja curto o suficiente para estar em um mesmo período do ciclo de negócios, fazendo com que c seja igual a 1. Além disso, caso haja sazonalidade, as variações ocorram ao acaso e possam ser reunidas em um só efeito, o modelo simplificado passa a ser (Afilal et al., 2016):
em que s incorpora o efeito sazonal e as variações ao acaso.
Os valores de T são oriundos da linha de tendência, ajustada conforme os valores reais da demanda conforme uma regressão simples em que a outra variável é o tempo. Caracteriza-se s como índices sazonais. Sua determinação é feita pela observação do afastamento dos valores reais da demanda e dos valores previstos pela linha de tendência pretérita. A previsão y também pode receber o nome de previsão corrigida pelo efeito sazonal (Mancuzo, 2003).
Existe um conjunto de modelos utilizados como métodos das médias. Entretanto, vale ressaltar que a previsão é sempre calculada por meio de algum tipo de média em que se utilizam valores reais anteriores da demanda. Ao contrário do que acontece com as regressões, é possível apenas prever um período à frente, apesar da possibilidade de se conceber adaptações para a obtenção de um maior número de previsões futuras. Além disso, à cada nova previsão são excluídos, ou mais fracamente ponderados, os valores mais antigos da demanda real e, por sua vez, são incluídos os mais novos. Isso em função de as médias serem móveis (van der Laan et al., 2016).
No modelo de média móvel simples (MMS), a previsão para o período t, ou seja, imediatamente futuro, é obtida pela média aritmética dos n valores reais da demanda imediatamente passados. A demanda é variável e pode ser suavizada usando vários períodos anteriores (Fortsch & Khapalova, 2016). Aplica-se o método da média móvel simples nos casos em que a demanda é estacionária, quando ela varia em torno de um valor médio (Li et al, 2017). Embora identifique uma variação na média, esse método faz com que a reação seja lenta. Porém, em situações de demandas crescentes ou decrescentes no decorrer do tempo, a tendência é de que a previsão fornecida por MMS esteja descompassada em relação aos valores reais. Portanto, esse método não se caracteriza como de alta eficiência para captar as variações sazonais, podendo até inclusive escondê-las, de acordo com o valor escolhido para n.
O modelo da média móvel ponderada (MMP) tem semelhança com o modelo MMS ao considerar n valores reais anteriores da demanda para a composição da média. Em compensação, são atribuídos pesos distintos para os valores, com vistas a uma maior importância aos dados mais recentes gerados da demanda. Assim, os valores mais recentes da demanda recebem maior importância, possibilitando revelar alguma tendência (van der Laan et al, 2016). Entretanto, quanto maior for o valor n, mais a previsão suavizará os efeitos sazonais e mais com menor agilidade responderá a variações na demanda.
Também é bastante utilizado o modelo da média móvel exponencialmente ponderada quando a demanda é variável e pode ser suavizada usando períodos anteriores (Tratar, 2015). Nesse modelo, as demandas recentes são mais relevantes para o período atual e o peso da relevância diminui exponencialmente à medida que há afastamento do período presente (Fortsch & Khapalova, 2016).
No modelo da média móvel exponencialmente ponderadas de 1a ordem (MMEPI), a previsão opera um período imediatamente à frente. Mas, com adaptações possíveis, pode-se estender a previsão para vários períodos à frente. O modelo MMEPI permite suavizar os picos de dados, considerar os dados anteriores incorporando as características de comportamento da série temporal e possibilita que o peso atribuído aos dados passados seja progressivamente menor. Além disso, o seu cálculo é simples, necessitando apenas dos dados mais recentes (Lucas & Zhang, 2016). A previsão para o período t, nesse modelo, é dada pela equação (14).
em que:
D t = previsão para o período t;
Dt-1 = previsão para o período (t-1);
α = constante de suavização;
V t-1 = demanda real para o período (t-1).
Para qualquer período de previsão desejado, haverá sempre a necessidade da previsão do período imediatamente anterior. Ao iniciar uma sequência de previsões, deve-se obter o primeiro valor de alguma outra maneira sem utilizar a equação. Além disso, é preciso definir o valor atribuído a constante de suavização, entre 0 e 1.
Outro modelo bastante parecido com o MMEPI é a média móvel exponencialmente ponderada de 2a ordem (MMEP2), que corresponde ao que se chama "dupla suavização" ou "duplo alisamento", demonstrado pela equação (15). É o mesmo modelo utilizado na MMEPI, porém o MMEP2 é aplicado sobre a previsão obtida pelo MMEPI.
em que:
D't = previsão de 2a ordem para o período t;
D't-1 = previsão de 2a ordem para o período (t-1);
β= constante de suavização de 2a ordem;
D t-1 = previsão de 1a ordem para o período (t-1).
Para P, tanto quanto em α, os valores variam entre 0 e 1. Então, a previsão com a MMEPI assume o papel que cabia aos dados reais e a nova previsão com a MMEP2 apresenta-se menos sujeita a variações bruscas. Além disso, em um dado período, percebe-se a relação:
A diferença entre a demanda real e a previsão gerada pela MMEPI é aproximadamente igual à diferença entre MMEPI e os resultados calculados de MMEP2. Tal relação permite corrigir a lacuna gerada entre a previsão de 1a ordem e a demanda real, denominado como "correção do efeito de tendência". Por meio dessa correção, é desenvolvida uma terceira previsão com valores reais mais próximos dos reais e escrita da seguinte maneira:
em que:
D c = demanda corrigida pelo efeito de tendência.
Certos modelos de suavização exponencial usam uma ponderação para cada valor observado na série temporal. Neste caso, valores mais recentes recebem pesos maiores, compondo um conjunto que decai exponencialmente partindo dos valores mais recentes (Fortsch & Khapalova, 2016).
A previsão de demanda pela suavização exponencial é realizada por meio do cálculo da média e da tendência, utilizando-se como base dados históricos (Syntetos et al., 2015). Entretanto, deve-se primeiro limpar e dessazonalizar os dados, por meio da seleção de fatores de suavização razoáveis.
Os métodos de suavização exponencial trazem como diferencial a possibilidade de identificar informações geradas pela série e explorar as influências apresentadas nas observações. Nesse sentido, quando um fato externo provoca mudanças de valores da variável em estudo, a consequência desse fato já está contemplada nos valores observados passados que resultarão em respostas futuras (Deb et al., 2017).
Um dos métodos mais utilizados é o método linear de Holt, que pode ser utilizado em séries temporais que apresentem tendência linear (Tratar et al., 2016). O método emprega duas constantes de suavização, α e β, cujos valores variam entre 0 e 1. O método é representado pelo conjunto equações abaixo:
As equações (18) e (19) fazem uma estimativa do nível e da inclinação da série temporal, respectivamente. A equação (20) calcula a previsão da demanda dos k períodos à frente.
Do mesmo modo que na suavização exponencial simples, o método de Holt requer valores iniciais para L 0 e T 0 . Como meio para os cálculos iniciais, pode-se utilizar em L 0 o último valor observado na série temporal e calcular uma média da declividade nas últimas observações para L 0 . A regressão linear simples também pode ser aplicada aos dados da série temporal, em que se obtém o valor da decli-vidade da série temporal e de L 0 em sua origem.
Os valores das constantes de suavização no método de Holt podem ser calculados do mesmo modo da suavização exponencial simples. São realizadas combinações de valores para a e p que proporcione a menor média do quadrado dos erros (Tratar, 2015).
Já os métodos de Winters descrevem dados de demanda que simultaneamente apresentem tendência linear e sazonalidade. De acordo com Aboagye-Sarfo et al. (2015), os modelos de Winters são divididos em aditivo e multiplicativo. O método aditivo apresenta a amplitude da variação sazonal constante ao longo do tempo. No método multiplicativo, a amplitude da variação sazonal aumenta ou diminui no decorrer do tempo.
O método multiplicativo de Winters, utilizado em situações em que os dados de amplitude do ciclo sazonal variam com o passar do tempo, é representado abaixo:
em que:
S = período completo de sazonalidade;
L t = nível da série;
T t = tendência;
S t = sazonalidade;
z t + k = previsão para k períodos;
Y = constante de suavização associada ao peso relativo à sazonalidade, utiliza-se entre 0 e 1.
Para dar início aos cálculos, os métodos de Winters necessitam valores iniciais para nível, tendência e sazonalidade. Para a estimativa da sazonalidade, é preciso ao menos um período sazonal completo de observações. Estimativas iniciais do nível e da tendência são realizadas no período s definido para o componente sazonal.
Para o método aditivo de Winters, conforme segue o conjunto de equações abaixo, são utilizados dados sazonais em que a amplitude do ciclo sazonal permanece constante com o passar do tempo (Petropoulos et al., 2018). O cálculo da tendência é o mesmo do método multiplicativo, entretanto o componente sazonal possui operações de soma e subtração, em oposição à operação de multiplicar e dividir.
Valores iniciais de L s e de T s são obtidos de modo idêntico ao método multiplicativo. Os componentes sazonais são calculados pela equação (29).
Os métodos autorregressivos integrados à média móvel ou Arima, também chamados de "modelos de Box-Jenkins", foram propostos por George Box e Gwilym Jenkins nos anos 1970 (Stúker, 2014). Os métodos Arima originam-se da ideia de que os valores de uma série temporal apresentam alta dependência entre si, portanto cada valor pode ser explicado por valores prévios da série (Brentan et al., 2017). A abordagem Box-Jenkins assume que o padrão de variabilidade nos dados é constante e o método usa um procedimento iterativo para ajustar um modelo de previsão baseado em padrões aleatórios e cíclicos de demanda para minimizar erros de previsão (Fortsch & Kha-palova, 2016).
Os modelos de Box-Jenkins preveem que muitos fenómenos não são de natureza determinística, devido à incidência aleatória de fatores desconhecidos, e os padrões históricos não se repetem consistentemente (Fortsch & Khapalova, 2016). Nesses casos, a previsão do valor futuro está sujeita a um cálculo de probabilidade e são aplicados métodos matemáticos para analisar tais sistemas, ditos "estocás-ticos". Processos estocásticos são caracterizados por um conjunto de variáveis aleatórias que descrevem a evolução de determinado fenómeno de interesse. Além disso, existe uma importante classe de modelos estocásticos utilizados na representação de séries temporais que são denominadas "modelos estacionários" (Joo & Kim, 2015), os quais consideram um processo sob equilíbrio, em que o conjunto de variáveis permanece em um nível constante médio. Por sua vez, existem séries temporais que possuem melhor representação com a utilização de modelos não estacionários (Wang et al., 2015).
Os modelos estocásticos partem da premissa de que uma série temporal, admitindo valores sucessivos e altamente dependentes, pode ser estimada a partir de uma série de ruído aleatório e transformada por meio de uma função matemática (Fortsch & Khapalova, 2016). O ruído aleatório a t é transformado na série temporal z t por uma função de filtro linear, que faz uma soma ponderada de ruídos aleatórios prévios e exposta na equação (30).
em que:
μ = nível do processo;
B= operador de defasagem;
Ψ(B)= função de transferência do filtro ou operador de linha que transforma a t em z t tendência.
Esses modelos podem representar tanto séries estacionárias quanto séries não estacionárias. Em uma sequência de infinita ou infinita e convergente, o processo z t se caracteriza como estacionário e com média ju. Em situação oposta, z t é não estacionário e u torna-se um ponto de referência para o nível do processo em algum momento no tempo.
Para a análise de séries temporais, o coeficiente de auto-correlação p descreve a correlação entre dois valores da mesma série temporal em diferentes períodos de tempo (Carvalho-Silva et al., 2018). O coeficiente de autocorre-lação p mede a correlação entre dois valores adjacentes na série e a autocorrelação é chamada "autocorrelação de lag" ou "defasagem" (Villani et al., 2017). Assim, o coeficiente de autocorrelação pk mede a correlação entre observações distantes k períodos de tempo, dita "autocor-relação de lag k" (Boroojeni et al., 2017).
em que:
σ x 2 = variância da série temporal.
Para uma estimativa do coeficiente de autocorrelação populacional p k , é utilizado o coeficiente de autocorrelação amostral demonstrado na equação (34) (Zhu et al., 2015). O número de autocorrelações de lags diferentes é calculado para a análise da série temporal pela relação N/4, em que N é o número total de observações na série.
em que:
k = 0, 1, 2, 3, N.
Nos modelos estocásticos em que existe muitas séries temporais, o modelo autorregressivo passa a ser aplicado como uma combinação linear finita de valores anteriores do processo e um ruído aleatório at (Boroojeni et al., 2017). Nesse modelo, os valores observados de um processo em espaços de tempo são igualmente divididos t, t -1, t -2 e, assim por diante, por Z t , Z t - 1, Z t-2 etc. Além disso, são denominados, Z t-1 , Z t - 2 etc. como os desvios da média u, representado na equação (36).
Um processo autorregressivo de ordem p,também chamado "AR(P)", é expresso na equação (37). É autorregres-sivo, porque o modelo linear ilustrado na equação (38) apresenta uma variável dependente Z a um grupo de variáveis independentes X 1 , X 2 , até Xp, com um termo de erro α e geralmente referido como um modelo de regressão, sendo Z regredido em X1, X2, Xp.
Os coeficientes autorregressivos Φ 1 , Φ 2 , até Φp são parâmetros que descrevem como um valor corrente Zt está relacionado com valores passados de Z t-1 ,, Z t-2 , até Z t-p . Já o coeficiente autorregressivo de ordem p, usando a definição do operador B, pode ser representado matematicamente pelo modelo autorregressivo simplificado na equação (39).
Para Z em modelos de média móvel, a observação Z t é subtraída da média u, dependendo linearmente de um número finito q de valores prévios do ruído aleatório at. Assim, obtém-se um processo de média móvel de ordem q, na equação (40), que expressa o valor atual de uma série temporal como valores atuais e q anteriores com ruídos aleatórios (Wang et al, 2015). O coeficiente de média móvel θ, de ordem q, pode usar a definição do operador B e ser representado matematicamente, de modo simplificado, pela equação (41).
Nesse caso, a série finita ilustrada na equação (42) não apresenta restrição sobre os parâmetros do processo de média móvel para assegurar estacionariedade.
A função de autocorrelação de um processo MA(q) é descrita pela equação (43).
em que:
k = 1, 2, q;
p k = 0, quando k > q.
Porém, ocorrem casos em que algumas séries temporais são mais bem modeladas por termos autorregressivos e de média móvel, resultando em um modelo misto de au-torregressivo com média móvel de ordem p( , q), conforme equação (44) (Joo & Kim, 2015). Para tanto, utiliza-se a notação do operador de defasagem B, conforme a equação (45), sendo abreviado para Arma p( , q). Os valores de p e q, na prática, são menores do que 2 para os casos de séries temporais estacionárias. O valor da média móvel é obtido usando uma combinação linear dos movimentos dos erros passados e não simplesmente as médias ponderadas dos valores passados (Fortsch & Khapalova, 2016).
Os modelos Arma partem do pressuposto de que pode existir um algum tipo de comportamento uniforme no padrão histórico dos dados, que pode ser usado para prever a demanda, embora o comportamento geral das séries temporais possa mudar de um período para o seguinte (Wu et al, 2017). Os comportamentos históricos podem incluir aleatoriedade, ciclicidade ou mesmo sazonalidade da demanda, que pode se repetir de maneira sequencial e previsível (Fortsch & Khapalova, 2016). As condições de estacionariedade e de invertibilidade são associadas a um modelo Arma p( , q) estacionário se as raízes do polinómio Φ (B)=0 corresponderem à área fora do círculo unitário. Caso as raízes de Φ (B)=0 estejam fora do círculo unitário, considera-se este como invertível (Mancuzo, 2003).
Muitas séries temporais apresentam variações sazonais. São séries que apresentam uma característica periódica a cada s intervalos de tempo, como o que acontece em séries compostas por observações mensais e de sazonalidade anual, sendo s associado ao valor 12. Nos modelos sazonais, tem-se um operador de diferença sazonal (Zhu et al., 2015), descrito na equação (46), intitulado como primeira diferenciação sazonal.
Muitas diferenciações sazonais, D, podem ser necessárias em uma série estacionária. Portanto, a forma geral do modelo sazonal autorregressivo integrado à média móvel de ordem (P, D, Q) pode ser apresentada como na equação (47) (Zhu et al, 2015).
em que:
Φ(B s ) = polinômio em Bs de grau P;
θ(B s ) = polinômio em Bs de grau Q.
P, D e Q = letras maiúsculas para diferenciar da representação nos modelos não sazonais.
Os componentes de erro geralmente estão correlacionados. Desse modo, é utilizado um segundo modelo descrito na equação (48) (Luo et al., 2017).
em que:
α t = processo de ruído aleatório;
Φ(B) = polinômio em B de grau p;
θ(B) = polinômio em B de grau q.
Com base nas equações anteriores, é possível obter um modelo multiplicativo geral, exposto na equação (49), e chamado de processo multiplicativo de ordem (P, D, Q) por (P, D, Q) (Luo et al., 2017).
Métodos com base em inteligência artificial
Os métodos baseados em computação imitam algumas das capacidades de processamento do cérebro humano para modelar situações simples e complexas. Esses modelos que utilizam a inteligência artificial apresentam a capacidade de identificar relacionamentos não lineares e interativos. Os métodos com base em inteligência artificial foram usados em sistemas de previsão de demanda ou como pré-processadores de dados para suavizar e classificar dados ruidosos para combinar as relações entre funções complicadas (Wang et al., 2018).
Na última década, as redes neurais artificiais receberam bastante atenção de pesquisadores e foram consideradas uma poderosa ferramenta computacional para resolver problemas complexos. As redes neurais são projetadas para captar padrões não lineares de séries temporais longas (Fiot & Dinuzzo, 2016). Técnicas neurais artificiais têm sido empregadas recentemente e com resultados bem-sucedidos em previsão de demanda e previsão de vendas em aplicações biomédicas, aeroespacial, indústria automotiva, ele-trónica, indústria financeira etc. (Raza & Khosravi, 2015).
Redes neurais artificiais são técnicas de modelagem semelhante ao funcionamento do cérebro humano. A rede de neurónios artificialmente interconectados explora múltiplas hipóteses concorrentes por meio de processamento simultâneo (Qiu et al., 2017). No cérebro humano, existem unidades de processamento - neurónios - que atuam em paralelo para o processamento e a coleta de dados. Os neurónios são conectados com pesos sinápticos e des-cobriu-se que essas conexões ou "pesos" são capazes de armazenar algum tipo de informação que pode ser recuperada posteriormente (Deb et al., 2017).
A rede neural é composta de um conjunto de neurónios ligados entre si e apresentando diferentes coeficientes de conectividade. Os coeficientes de conectividade representam os pontos fortes das conexões (Ren et al., 2016). A aprendizagem acontece pelo ajuste da força de conexão para que os neurónios possam ser agrupados em camadas. A rede neural pode ser de camada única ou multicamadas (Chae et al., 2016). A rede neural multicamadas detém uma ou mais camadas ocultas entre as camadas de entrada e saída da rede e apresenta melhor capacidade de aprendizado e de produzir uma melhor saída do que a rede neural de camada única (Raza & Khosravi, 2015).
No modelo matemático da rede neural, o objetivo principal é identificar os pesos treinando o modelo com dados registrados no passado, que geralmente são organizados em conjuntos de entradas e saídas (Deb et al., 2017). A rede neural extrai a relação não linear entre variáveis usando o processo de treinamento da rede (Ke et al., 2017). A rede pode aprender o comportamento de saída da demanda usando a função de reorganização de padrão. No entanto, os padrões de saída são aprendidos a partir da aplicação dos padrões de dados de treinamento de entrada para treinar a rede (Aizenberg et al., 2016).
Outro método que utiliza inteligência artificial, bastante comum, é a lógica difusa (Fuzzy Logic). Foi apresentada por Takagi e Sugeno (1985) como uma abordagem de análise numérica para sistemas difusos. São observações de séries temporais com valores linguísticos em vez dos valores numéricos convencionais de observações. Diferentemente dos métodos estatísticos, em séries difusas, não há hipóteses restritivas, como pressupostos estacionários ou lineares a serem cumpridos. Além disso, podem lidar com problemas ou situações não lineares quando o conjunto de dados são disponibilizados em termos linguísticos (Efendi et al., 2015).
Segundo Guo et al. (2018), geralmente a etapa inicial do projeto é particionar o universo de valores das séries temporais em intervalos iguais ou desiguais, e então conjuntos difusos são definidos com base nesses intervalos. É um sistema de regras "se então" que pode modelar os aspectos qualitativos do conhecimento humano e o processo de raciocínio sem o emprego de análises quantitativas. Os conjuntos difusos, proposto inicialmente por Zadeh (1965), são normalmente dados de maneira subjetiva e não refletem totalmente os dados existentes. Apesar de a especialização humana desempenhar um papel fundamental na formação de conjuntos difusos, as características dos dados não são totalmente capturadas dessa maneira (Guo et al, 2018).
As relações lógicas difusas são formadas com base nos grupos de amostras. Então são determinados os grupos de relações lógicas difusas dividindo os relacionamentos lógicos difusos derivados em grupos com base nos estados atuais. Assim, é possível usar esses relacionamentos lógicos para realizar a previsão (Efendi et al., 2015).
Existem muitas abordagens nas quais a lógica difusa pode ser determinada, inclusive, por meio de redes neurais artificiais devido à eficácia significativa da etapa de determinação da relação difusa no desempenho da previsão. Portanto, o desempenho da previsão pode ser significativamente aumentado pela utilização de redes neurais na determinação de relações difusas (Kocak, 2017). Os sistemas neuro-fuzzy combinam a lógica difusa baseados em regras com a capacidade de aprendizagem de redes neurais. Segundo Raza e Khosravi (2015), a modelagem neuro-fuzzy tem sido reconhecida como uma ferramenta poderosa e que pode facilitar o desenvolvimento de novos modelos pela combinação de informações de diversas fontes, tais como modelos empíricos, heurística e dados.
Por sua vez, séries temporais aparentemente complexas têm sido melhor compreendidas usando modelos caóticos não lineares em comparação com técnicas estocásticas. O método (k-nn) mais próximo é um dos métodos de previsão de fluxo caótico mais empregados (Tongal & Berndtsson, 2017). Um sistema caótico apresenta flutuações da saída limitadas a uma estrutura não linear, expressando um comportamento caótico que reage intensamente a variações nas condições iniciais, mas de acordo com propriedades determinísticas. Apesar de inesperadas, as saídas de um sistema caótico não são aleatórias, havendo correlação entre saídas em instantes de tempo diferentes (Jamil & Zeeshan, 2018).
Modelos caóticos descrevem fenómenos com leis de formação determinística, mas que, à primeira vista, parecem ser aleatórios (Sellitto et al., 2018). A teoria do caos permite a avaliação da interação entre as variáveis e revela padrões complexos que governam o comportamento dos sistemas sem a necessidade de avaliar cada variável potencialmente relevante. Portanto, pode detectar com precisão padrões de processos dinâmicos determinísticos que podem parecer estocásticos e lidar com a escassez de dados, já que é capaz de discriminar padrões determinísticos e sistemas aleatórios genuínos sem a necessidade de conjuntos extensos de dados (Tapia Cortez, Saydam et al, 2018).
Os modelos caóticos podem ser aplicados em pesquisas e situações similares a de Sellitto et al. (2017) sobre empresas que operam em cluster, no sentido de antever e prever aspectos estratégicos de produto e do negócio. Conforme exposto em Sellitto e Luchese (2018), foram pesquisadas as práticas de cooperação entre concorrentes de um cluster e percebeu-se a necessidade de detectar a presença e, caso ocorra, medir a intensidade das dimensões de benefício mútuo, confiança e comprometimento subjacentes à cooperação em relação ao concorrente, podendo-se também fazer uso dos modelos caóticos.
Apesar de serem originados de regras determinísticas, pela recorrência de aplicação da regra e sob certas circunstâncias, os fenómenos caóticos passam a ser imprevisíveis em longo prazo. A extrema dependência das condições iniciais dos parâmetros determina que a produção de um fenómeno caótico se torne instável ao longo do tempo e, por consequência, os resultados de sistemas determinísticos, mesmo com leis de evolução definidas, são extremamente sensíveis a perturbações e ruído, tornando-os de difícil previsibilidade. Mesmo na ausência de ruído, as não lineari-dades e as interações entre os componentes amplificam erros mínimos nos parâmetros, gerando o caos determinístico (Sellitto et al, 2018).
As propriedades importantes para reconstruir a dinâmica dos sistemas caóticos são chamadas "dimensão de incorporação" e "atraso de tempo". A dimensão de incorporação corresponde ao número de variáveis que governam o sistema. O atraso temporal corresponde à influência temporal das variáveis, ou seja, por quanto tempo as mudanças das variáveis podem afetar o sistema. O Teorema de Taken, que é um dos teoremas mais conhecidos e usados para reconhecer o comportamento caótico em séries temporais, indica que a dinâmica do sistema pode ser reconstruída pela reorganização da sequência de observações de séries temporais e que mudanças em suas formas fornecem informações significativas escondidas dentro da dinâmica do sistema (Tapia Cortez, Hitch et al, 2018).
Conclusões
No presente artigo, foi apresentada uma revisão da literatura dos métodos de previsão de demanda, reunindo os métodos e os modelos disponíveis acerca dos conceitos utilizados atualmente na administração de empresas relacionados ao consumo e à produção de produtos e serviços. Póde-se contemplar os métodos qualitativos, quantitativos e com base em inteligência artificial em pesquisa acadêmica única, exposta em forma de síntese na tabela 2. Também se evidenciaram as diferentes técnicas e métodos empregados recentemente e que proporcionam resultados bem-sucedidos em previsão de demanda e previsão de vendas em aplicações diversas como biomédicas, aeroespacial, indústria automotiva, segmento de eletró-nica, geração de energia, setor financeiro etc. (Raza & Khosravi, 2015).
Tabela 2 Síntese dos métodos de previsão de demanda
| Método | Abordagem | |
|---|---|---|
| Qualitativos | Julgamento por especialistas | Utiliza a opinião e a experiência de especialistas para criar a predição de demanda. Os dados resultantes são convertidos em um modelo que estima uma regressão em função do conjunto de previsões coletadas. As previsões são de longo prazo, envolvendo aspectos do planejamento estratégico da empresa. |
| Delphi | Emprega um questionário que é enviado a especialistas, cujas respostas são analisadas, resumidas e retornadas anonimamente diversas vezes aos respondentes. Aplicado a fenómenos complexos e subexplo-rados na previsão de ciência e tecnologia, previsão de negócios e elaboração de políticas participativas. | |
| Método de analogia estruturada | Prepara-se uma descrição da situação objetivo e selecionam-se especialistas que conheçam situações análogas. Os especialistas identificam e descrevem situações similares, classificam sua semelhança com a situação-alvo e combinam os resultados de suas analogias com resultados potenciais dessa situação-alvo. | |
| Pesquisa de intenção e opinião | Utilizadas para verificar as intenções de compra ou padrões de comportamento referentes à determinadas condições. É realizada com a intenção de perceber os atributos que levariam a uma opção de compra ou um padrão de comportamento. | |
| Quantitativo | Regressão linear: simples e múltipla | Avalia o relacionamento entre o que se pretende prever, denominada "variável dependente" (Y), e os fatores que determinam o valor de Y, denominadas "variáveis independentes" (Xi). Os dados consistem em observações, cada uma delas com medidas em períodos diferentes. São úteis para prever pontos de inflexão no comportamento da demanda e para as previsões de longo prazo. |
| Séries temporais: média móvel simples, média móvel ponderada, média móvel exponencialmente ponderada, suavização exponencial, Arma e Arima | Conjunto de observações geradas sequencialmente no tempo, que examina o padrão de comportamento passado de um fenómeno ao longo do tempo para prever o comportamento futuro. São métodos utilizados para fazer previsões de curto prazo quando os valores das observações ocorrem conforme um padrão de comportamento identificável ao longo do tempo. | |
| Inteligência artificial | Redes neurais | São projetadas para captar padrões não lineares de séries temporais longas. O modelo com dados registrados no passado, são organizados em conjuntos de entradas e saídas. A rede pode aprender o comportamento de saída da demanda usando a função de reorganização de padrão. Os padrões de saída são aprendidos aplicando os padrões de dados de treinamento de entrada para treinar a rede. |
| Lógica difusa | São observações de séries temporais com valores linguísticos em vez dos valores numéricos convencionais de observações. É um sistema de regras "se então" que pode modelar os aspectos qualitativos do conhecimento humano e o processo de raciocínio sem o emprego de análises quantitativas. São determinados os grupos de relações lógicas difusas dividindo os relacionamentos lógicos difusos derivados em grupos com base nos estados atuais, assim, possibilitam usar esses relacionamentos lógicos para realizar a previsão. | |
| Sistemas neuro-fuzzy | Combinam a lógica difusa baseados em regras com a capacidade de aprendizagem de redes neurais. Reconhecida como uma ferramenta poderosa e que pode facilitar o desenvolvimento de novos modelos pela combinação de informações diversas e a resolução de problemas complexos em previsão de demanda. | |
| Modelos caóticos | Avalia a interação entre variáveis e revela padrões complexos que governam o comportamento dos sistemas. Pode detectar com precisão padrões de processos dinâmicos determinísticos que podem parecer estocásticos e lida com a escassez de dados. Reconhece o comportamento caótico em séries temporais e indica a dinâmica do sistema que pode ser reconstruída pela reorganização da sequência de observações de séries temporais e as mudanças em suas formas fornecem informações significativas escondidas dentro da dinâmica do sistema. | |
Fonte: elaboração própria.
Os métodos qualitativos são recomendados quando não há dados quantitativos históricos disponíveis ou quando esses dados não forem confiáveis. São métodos que utilizam a expertise da equipe de especialistas, o que permite alta flexibilidade e análises mais amplas sobre aspectos estratégicos. Os métodos qualitativos e os métodos causais, utilizados em previsões de médio e longo prazos, demonstram serem simples na implantação.
Os métodos causais são os que melhor representam a relação entre os fatores a serem previstos, bem como outros fatores internos e externos podem ser identificados e considerados. São úteis para prever pontos de inflexão na demanda e fornecem os subsídios para previsões mais sofisticadas.
A análise de séries temporais, especificamente pelos métodos que utilizam médias e os métodos que envolvem suavização exponencial, indica melhores resultados nas previsões de curto prazo. São os métodos mais simples para a análise de séries temporais, oferecem bons resultados e são os mais utilizados em previsão de demanda de um modo geral. Além disso, requerem recursos computacionais pouco complexos.
Os métodos que utilizam inteligência artificial modelam situações simples e complexas, e apresentam a capacidade de identificar relacionamentos não lineares e interativos, sendo aplicados em sistemas de previsão de demanda ou como pré-processadores de dados para suavizar e classificar dados ruidosos para combinar as relações entre funções complicadas. São recomendados para situações que requerem análises de realidades complexas e, por isso, demandam de recursos operacionais e computacionais mais qualificados.
É necessário avaliar e testar diversos modelos parca encontrar o que seja o mais adequado à realidade que se está analisando. Um recurso utilizado em diversas realidades é a construção de um modelo próprio de previsão de demanda utilizando técnicas, aspectos, conceitos e características de diferentes métodos e modelos. Entretanto, é fundamental monitorar o modelo adotado por meio da medição do erro de previsão a fim de exercer o controle do modelo e efetuar correções o mais rápido possível.
Estudos relacionados à previsão de demanda apresentam oportunidades de maiores pesquisas, sendo oportuna a incorporação de conceitos adicionais, como finanças e contabilidades de custos. Estudos que envolvem planejamento de capacidade operacionais, acuracidade das previsões, controle de recursos, bem como métodos de controle de custos integrados à previsão de demanda trariam significativa contribuição.
Sugere-se a realização de novos estudos de revisão da literatura e de bibliometria que associem análises estatística do número de citações dos artigos selecionados, bem como a realização de estudos estatísticos relacionados individualmente aos métodos de previsão de demanda. Estudos com base em artigos com mais de cinco anos de publicação são recomendados a fim de obter uma visão das pesquisas seminais por métodos de previsão e, ainda, indicar modificações, adaptações e incorporações de recursos aplicados nos métodos e modelos.