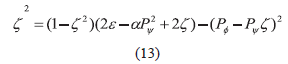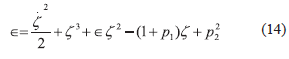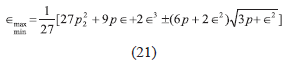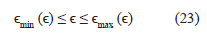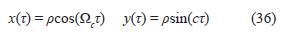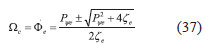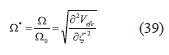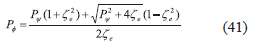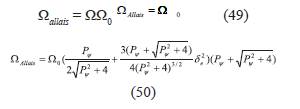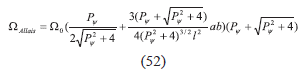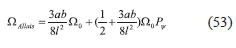Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. INTRODUCCIÓN
El péndulo físico en su versión más simple es un sólido rígido de forma arbitraria que puede oscilar en un plano vertical que contenga a su centro de masa, alrededor de un eje perpendicular a dicho plano. El punto de intersección del eje con el plano es el punto de suspensión. Cuando el punto de suspensión se sustituye por un soporte que le permita al péndulo oscilar en todo el ángulo sólido que rodea al eje del cuerpo que pasa por su centro de masa y el punto de suspensión, y le permita además rotar alrededor de dicho eje, tenemos un péndulo físico con tres grados de libertad [1]. Debido a la rotación de la tierra, es claro que en un sistema inercial de referencia la precesión y el espín inicial son muy pequeños, del orden de 10-4 rad/s, esto hace que la nutación se constituya en el movimiento dominante. En estas condiciones iniciales el péndulo describe trayectorias aproximadamente elípticas que precesan muy lentamente en un sistema de referencia inercial. A esta precesión la denominaremos precesión de Allais [2] y los resultados de este estudio representan una primera aproximación a la dinámica del péndulo físico asimétrico que es usado actualmente por muchos investigadores en el estudio de anomalías gravitacionales durante los eclipses [3, 4, 5].
Como veremos en este caso se distinguen tres modos de oscilación: el modo plano, el modo elíptico y el modo cónico.
En el modo plano el péndulo es soltado desde su posición inicial, sin ninguna velocidad transversal de manera que su momento angular es cero y el cuerpo describe su trayectoria sobre un arco de círculo vertical. En el modo elíptico el péndulo se mueve entre dos planos horizontales, se caracteriza porque el momento angular es distinto de cero y la trayectoria que describe es elíptica oblicua entre dos alturas [6]. Finalmente el péndulo se encuentra en su modo cónico cuando describe un movimiento circular uniforme a una altura fija, se distingue porque el momento angular es constante diferente de cero y el péndulo describe una trayectoria circular en un plano horizontal.
En este articulo estudiaremos la dinámica del péndulo físico simétrico cuando es suspendido bajo condiciones iniciales similares a las que experimentaría cuando éste es soltado cerca de la superficie de la tierra con pequeñas amplitudes iniciales, sin ninguna componente de la velocidad transversal ni de espín; utilizando el potencial efectivo, en el cual este va a depender de la coordenada de la nutación y depende también paramétricamente de la energía y del momento angular del sistema. Además con este potencial efectivo realizaremos y analizaremos un estudio unificado en el espacio de fase de los distintos modos de oscilación mencionados anteriormente.
2. PÉNDULO FÍSICO SIMÉTRICO
Un péndulo físico simétrico (PFS) es un caso muy particular del trompo simétrico en el cual tiene un eje de simetría que puede girar libremente alrededor de un punto fijo o un soporte ubicado en un extremo del eje de simetría y el centro de masa se encuentra por debajo del punto fijo; por lo tanto los movimientos de precesión y espín se pueden considerar como pequeñas perturbaciones al movimiento de nutación dominante [1]. El ejemplo más simple consiste de una varilla cilíndrica colgada de uno de sus extremos, como se muestra en la Figura 1.
Figura 1 Péndulo Físico Simétrico. En la orientación del sistema de ejes inerciales XY Z: Φ, y Ψ son los ángulos de Euler usados en la descripción del movimiento.
A. Hamiltoniano del PFS
La energía cinética y potencial del sistema está dadas respectivamente por:
Donde su energía potencial es negativa, debida a que el péndulo está por debajo del punto fijo (soporte).
Por último, el Lagrangiano del sistema lo podemos escribir en términos de los ángulos de Euler como:
Donde
. son los momentos de inercia del péndulo con respecto a los ejes X y Z fijado al cuerpo. Las coordenadas Φ y Ψ son cíclicas, por lo tanto sus momentos generalizados asociados son constantes de movimiento:
De las ecuaciones (4) y (5) podemos llegar a:
Dado que el sistema es conservativo, la energía mecánica del sistema es:
En términos de variables canónicas tenemos:
O en unidades adimensionales se tiene:
Donde hemos utilizado las definiciones:
3. POTENCIAL EFECTIVO
Para un análisis cualitativo de la física involucrada en este sistema, es conveniente introducir un potencial efectivo asociado a la coordenada θ. Para ello despejamos θ2 en la ecuación (10), esto es:
Introduciendo la variable adimensional
en la ecuación (12); tenemos:
En función de los nuevos parámetros, la ecuación (13) nos queda:
Donde
Introduciendo en la ecuación (14) el potencial efectivo asociado a la variable ζ:
Donde
es una función de Z que depende de los parámetros ζ; e; p
1
y p
2
. Es decir:
Nótese también que estas raíces de esta ecuación
, corresponden a los ceros del polinomio cúbico de la ecuación (17) y físicamente representa los puntos de retornos en la coordenada ζ.
Los puntos críticos de este potencial se obtienen derivando e igualando a cero, estos es:
Esta ecuación nos va a permitir obtener un criterio para las energías que son físicamente aceptadas, cuando variamos las condiciones iniciales y al parámetro Є.
Las raíces de esta ecuación son:
Lo cual nos muestra que ζ max <0 y ζ min >0; estos puntos dependen de las energías y de los momentos con respecto a Φ y Ψ.
Los valores del potencial efectivo asociado a estos puntos críticos son:
Donde:
Con p = 1 + p1
En la figura 2 se muestra el péndulo que se mueve con Є = 0,45; p1 = 1; p2 = 1. También podemos observar que con el fin de mantener el movimiento siempre acotado y en la región de interés físico se cumple que:
De la figura se puede notar que Є max > Є para toda Є; p 1 y p 2 luego podemos concluir que las energías y las condiciones iniciales físicamente aceptadas satisfacen:
Donde Є max no es una cota superior, es una función que depende de la energía total del sistema.
4. MODOS DE OSCILACIÓN
Nos restringiremos ahora a las condiciones iniciales propias de un PFS que es soltado cerca de la superficie de la tierra con condiciones iniciales propias del modo plano, vemos que PΨ ≈ P Φ , ≈ 10-2 y P1 ≈ 102, por lo tanto la precesión y el espín son solo pequeñas perturbaciones al movimiento de nutación dominante (θ≈ 10-1).
4.1 Modo plano
El modo plano se origina cuando el centro de masa del péndulo es soltado desde una posición inicial sin ninguna velocidad transversal, su característica principal es que Φ = 0. Para este modo tenemos:
Los puntos críticos y sus correspondientes energías son:
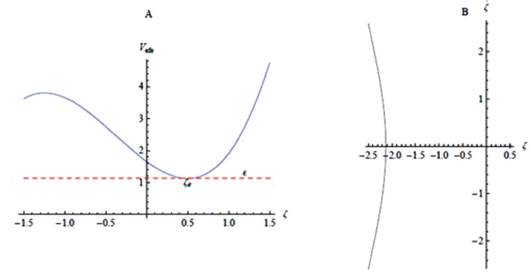
En la figura 3A, si la energía está en el intervalo ‒1 < Є < 1 el movimiento es acotado y oscilatorio en la región de interés físico. Para Є > 1 el péndulo produce un movimiento acotado en el intervalo ‒1 < ζ < 1 pasando por los puntos ζ = ± 1.
Figura 3 A: Potencial efectivo V efe en función de de ζ para ϵ = ‒1, ‒0.5, 1, 1.5 B: Curvas de fase ζ en función de ζ para los mismos valores de energías.
En la figura 3B todas las curvas de fase pasan por el punto ζ = 1 que corresponden a la posición más baja de todas las trayectorias posibles.
Observemos también que si Є = ‒1 entonces ζ = 1, por lo tanto el péndulo está colgando en su posición más baja en el punto (1,0), en este caso las energías menores no son físicamente aceptadas.
Si Є = 1 entonces ζ = ‒1, luego el péndulo está en su posición más alta en el punto (-1,0) en donde se presenta un punto de bifurcación; en este caso hay un punto de equilibrio inestable y con cualquier pequeña perturbación por mínima que sea, el péndulo se caer.
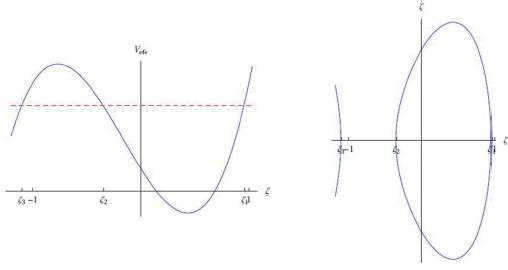
4.2 Modo elíptico
En este modo de oscilación el centro de masa del péndulo se mueve entre dos planos horizontales ζ = ζ2 y ζ = ζ1 donde ζ1 y ζ2 son los puntos de retornos del potencial efectivo (17) o raíces de (13). Este modo se caracteriza por p1 ≠ 0 y:
Estas condiciones implican que ζ3 < ‒1 < ζ2 < ζ1 < 1 como se muestran en la figura 4.
En la parte A de esta figura hemos graficado el comportamiento genérico del potencial efectivo, mientras que en la parte B su correspondiente diagrama de fase.
En el comportamiento genérico la raíz ζ3 viola la ligadura de modo que el movimiento periódico del péndulo es acotado y se cumple que ζ2 < ζ1 < 1; por otro lado en el eje horizontal de esta grafica se muestran los puntos de retornos ζ3 < ζ2 < ζ1 y el movimiento es acotado y físicamente aceptable para ζ3 ‒1 < ζ2 ≤ ζ < ζ1 < 1.
4.3 Modo cónico
En el modo cónico el centro de masa del péndulo describe un movimiento circular uniforme a una altura fija en un plano horizontal.
Se caracteriza por las siguientes condiciones:
En este caso ζ se mantendrá constante y por lo tanto podemos definir:
La energía e de este modo en función de las variables originales: es:
La frecuencia angular del movimiento circular es:
Notemos que hay dos frecuencias asociadas a la misma altura y al mismo espín; en este caso Φ+ representa la frecuencia angular del movimiento circular en sentido anti horario, es decir, hay una precesión rápida; mientras que Φ‒ es la frecuencia en sentido horario, en este caso hay una precesión lenta.
El espín con que está rotando el péndulo en este modo es:
En la figura 5 graficamos el potencial efectivo y su correspondiente diagrama de fase en función de ζ para Є = 0.5 en donde la región de interés físico está en el punto (0.69, 0).
5. PRECESIÓN APSIDAL DEL PFS
La deducción está basada en la teoría de pequeñas oscilaciones alrededor del movimiento estacionario, en este caso la trayectoria perturbada resulta de aplicar una pequeña perturbación al modo cónico o estacionario como se muestra en la figura 6.
Figura 6: La trayectoria perturbada (línea continua gruesa) está inscrita entre los círculos de radio α = ρe + x0 y b = ρe ‒ x0. La trayectoria estacionaria (línea a trazos) es circular y de radio ρe.
En esta figura el modo cónico está representado por la trayectoria circular de radio ρe (línea a trazos), mientras que la trayectoria perturbada (línea continua gruesa) es la elipse que está inscrita entre los círculos de radio α = ρe + x0 y b = ρe ‒ x0 donde x0 << 1 es la perturbación.
Las coordenadas horizontales x(τ) y y(τ) de este modo estacionario se pueden expresar como:
Y las correspondientes coordenadas de la trayectoria son:
Donde ρ(τ) = ρe + x0 cos(Ω*τ)
Ωc es la frecuencia circular del modo estacionario es:
La frecuencia angular de las pequeñas oscilaciones alrededor del movimiento estacionario está dada por:
En unidades adimensionales tenemos:
Derivando el potencial efectivo (17) y realizando las respectivas sustituciones en la ecuación (39) tenemos:
En este puno debemos recordar que el signo de Ωc da lugar a dos constantes Pϕ y por lo tanto a dos frecuencias Ω* para pequeñas alrededor del movimiento estacionario.
Si Ωc > 0
Luego la ecuación (40) nos queda:
La razón entre las dos frecuencias Ωc/ Ω la podemos expresar en términos de
y la expandimos en series de potencia de δe hasta segundo orden.
Que la órbita sea cerrada o precese depende de esta razón, es claro que esta orbita precesará, pues la razón anterior será en general mayor que ½. El tiempo que tarda ρ para ir de su eje mayor valor α = ρe + x0 a su valor mínimo b = ρe ‒ x0 es τ n = π / Ω* y en ese tiempo el ápside avanza un ángulo:
Cuando τ n = π / Ω* el ápside avanza un ángulo un poco mayor que π / 2 de modo que el exceso de ϕ sobre π / 2 es:
Entonces la velocidad angular de precesión de Allais en unidades adimensionales es:
Podemos ahora suponer que Ω* ≈ 2Ω c esto equivale a exigir que la trayectoria del movimiento perturbado sea aproximadamente elíptica. Luego la velocidad angular de precesión en unidades adimensionales es:
Usamos nuevamente la expresión (37) en términos de δ e .
En donde hemos expandido es serie de potencia de δ e y retenido sólo términos menores o iguales que δ e 2 , esto es debido a que la ecuación (47) es cuadrático en δ e y este es el orden hasta el cual queremos aproximar. Sustituyendo este resultado en (47) y usando las unidades estándar, tenemos para la precesión ápsidal de Allais:
Por otra parte tenemos:
La cual está perfectamente justificada si se tiene en cuenta que x 0 << 1 por ser una pequeña perturbación. Usando este resultado en (50) tenemos:
Esta ecuación es la aproximación hasta segundo orden en δ e para la frecuencia angular de precesión ápsidal de Allais para el modo elíptico y es válida para cuando las condiciones iniciales de este modo son ϕ 0 > 0. Estamos interesados en aplicar esta aproximación al caso de un PFS fijo en la superficie de la tierra en cuyo caso, esto motiva a realizar una expansión adicional en serie de potencia en P ψ y conservar solamente el término lineal.
Si Ωc < 0
Entonces
Repitiendo los mismos pasos del caso anterior obtenemos es:
Proponemos una última aproximación para el periodo de la coordenada θ, este periodo del movimiento elíptico. Es claro que este periodo es 4 veces τ n y en unidades estándar es:
Donde ζ e es la altura asociada al modo cónico estacionario:
CONCLUSIÓN
Hemos realizado un estudio unificado en el espacio de fase de los distintos modos de oscilación que se pueden presentar en la dinámica del PFS introduciendo un potencial efectivo, como una función que además de depender de la coordenada y el momento angular , también depende paramétricamente de la energía. Deducimos también la precesión ápsidal de Allais (53), considerando que el modo elíptico se puede obtener como el resultado de aplicar una pequeña perturbación al modo estacionario o modo cónico de este sistema. Esta deducción es conceptualmente más sencilla que la reportada en la literatura, pues se basa en la comparación de la frecuencia de las pequeñas oscilaciones alrededor de este modo. Una ventaja de este enfoque es que permite obtener expresiones analíticas aproximadas para el periodo del movimiento elíptico (56) y para la proyección de la trayectoria del modo de oscilación más general (58).
