1. Introducción
Las correlaciones cuánticas se han convertido en una herramienta clave para el estudio de la información, la criptografía y la teleportación cuántica, entre otras. Los estados cuánticos proporcionan nuevas formas de procesamiento de la información y comunicación sin análogos en la información clásica. El recurso esencial para la mayoría de estas aplicaciones son los estados entrelazados [1]. Sin embargo, el entrelazamiento es una propiedad difícil de alcanzar e incluso, cuando se logra, suelen ser estados cuánticos muy inestables, vulnerables bajo los efectos de cualquier proceso disipativo como resultado del acoplamiento al medio ambiente [2].
La dinámica de la decoherencia clásica y cuántica ha estimulado un gran interés en la investigación de los fenómenos de cambios repentinos en las correlaciones para diferentes sistemas físicos. Durante los últimos años, un esfuerzo intenso se ha centrado en explicar la naturaleza de las transiciones repentinas y los efectos de congelación de las correlaciones cuánticas y las condiciones bajo las cuales ocurren tales transiciones. Además, desde la perspectiva de las aplicaciones, la eficiencia con la que se podrían diseñar estos fenómenos en tecnologías cuánticas también es una cuestión de interés [3].
2. Modelo
Se consideran dos átomos de dos niveles localizados cada uno, en cavidades no interactuantes, las cuales interactúan con un reservorio común. Cada átomo interactúa con dos modos del campo electromagnético de frecuencias ω0 y ω1en su respectiva cavidad. En este sistema se tienen en cuenta las pérdidas bifotónicas a través de cada cavidad, como se muestra en la figura 1.

Figura 1 Dos cavidades distantes y no interactuantes, cada una con un átomo en su interior, inmersas en un baño térmico. En la figura y es la tasa de decaimiento de bifotones en cada cavidad.
El Hamiltoniano del sistema cerrado qubits cavidades se escribe como
donde
 es el Hamiltoniano libre de interacciones y está dado por,
es el Hamiltoniano libre de interacciones y está dado por,
Donde
 son los operadores aniquilación (creación) de los modos en cada cavidad, ω es la frecuencia de transición de cada átomo,
son los operadores aniquilación (creación) de los modos en cada cavidad, ω es la frecuencia de transición de cada átomo,
 z
j es el operador de inversión de población del átomo j.
z
j es el operador de inversión de población del átomo j.
Ĥ i corresponde al Hamiltoniano de interacción de cada átomo con los dos modos de la cavidad,
donde g es la constante de acoplamiento entre los modos del campo de la cavidad y los átomos,
 j
± son los operadores de transición entre los niveles de energía del átomo j [4].
j
± son los operadores de transición entre los niveles de energía del átomo j [4].
Para determinar las correlaciones cuánticas de los átomos se encuentra la solución de la ecuación maestra Lindblad del operador densidad atómico
 (t), que viene expresada como,
(t), que viene expresada como,
donde
 son los operadores colapso y ŝ = â
son los operadores colapso y ŝ = â
 corresponde a un operador colectivo del campo electromagnético. k es la constante de acoplamiento de las cavidades al baño térmico.
corresponde a un operador colectivo del campo electromagnético. k es la constante de acoplamiento de las cavidades al baño térmico.
 es el número de fotones térmicos a la temperatura T. H
s
es el Hamiltoniano del sistema qubits-cavidades [5].
es el número de fotones térmicos a la temperatura T. H
s
es el Hamiltoniano del sistema qubits-cavidades [5].
Por último se encuentran los elementos de matriz del operador densidad atómico en una base escogida y se calculan las correlaciones cuánticas (entrelazamiento y discordia).
3. Correlaciones Cuánticas
Con el fin de comprender el comportamiento de las correlaciones cuánticas, entrelazamiento y discordia, se describe el cálculo del grado de entrelazamiento de un sistema el cual se mide a partir de la concurrencia y se define la discordia cuántica como una medida alternativa de las correlaciones.
Existe una fórmula explícita de la concurrencia de un estado mixto arbitrario de dos qubits [7, 8]:
los λ i (i = 1,2,3,4) son valores propios, en orden decreciente de la matriz densidad no hermítica R , con
Para los estados separables C = 0 y para los máximamente entrelazados C = 1.
El entrelazamiento no es la única medida de las correlaciones cuánticas, por lo tanto se estudia un enfoque que cuantifica todas las correlaciones no clásicas presentes en un sistema además del entrelazamiento, la Discordia Cuántica es dada por la diferencia de información mutua y las correlaciones clásicas así [9, 10]:
Se define la información mutua como
donde
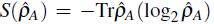 es la entropía de von Neumann para el sistema A y,
es la entropía de von Neumann para el sistema A y,
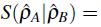
 es la entropía condicional de A con respecto a B.
es la entropía condicional de A con respecto a B.
y las correlaciones clásicas se calculan mediante,
donde
 es un conjunto de proyectores, que describen una medición realizada localmente en el sistema B.
es un conjunto de proyectores, que describen una medición realizada localmente en el sistema B.
La discordia proporciona información sobre la naturaleza cuántica de las correlaciones entre dos sistemas, de modo que es cero para los estados que únicamente tienen correlaciones clásicas y distinto de cero para los estados con correlaciones cuánticas. La discordia cuántica es igual al entrelazamiento de estados puros, y son distintos para estados mixtos, ya que algunos estados presentan una discordia cuántica finita incluso sin enredos [11].
4. Resultados
A continuación se presentan los resultados obtenidos del sistema estudiado. Todos los parámetros aquí son adimensionales, normalizados a la frecuencia del qubit (átomo de dos niveles). Como valores de referencia se podría considerar: ω = 2∏ x 1 GH z , y/ ω = 10-3 , g/ ω = 0.5 y ω0 + ωi = 0.9ω, parecidos a los de Ref. [3], y que están relacionados con experimentos modernos en cavity-QED [12]. Se ha considerado que los dos modos del campo electromagnético son iguales para realizar los cálculos numéricos. El estado inicial de las cavidades es el estado vacío. Los dos átomos inicialmente se consideran en un estado descrito por una matriz densidad tipo X en forma de Bloch como
donde
 es un vector dado por las matrices de Pauli, Î es la matriz identidad y el vector ĉ = (c1, c2, c3) definen completamente el estado, con -1 ≤ c
i
≤ 1. A continuación se muestran los resultados numéricos cuando no se tienen en cuenta las pérdidas de fotones (figura 2), y cuando se tienen en cuenta las perdidas unifotónicas y bifotónicas (figura 3).
es un vector dado por las matrices de Pauli, Î es la matriz identidad y el vector ĉ = (c1, c2, c3) definen completamente el estado, con -1 ≤ c
i
≤ 1. A continuación se muestran los resultados numéricos cuando no se tienen en cuenta las pérdidas de fotones (figura 2), y cuando se tienen en cuenta las perdidas unifotónicas y bifotónicas (figura 3).

Figura 2 Dinámica de las correlaciones sin pérdidas: (a) unifotónicas y (b) bifotónicas. Concurrencia (negro), Discordia (rojo) y Correlaciones clásicas (azul). El número promedio de fotones térmicos  = 20. El estado inicial de los qubits está definido por
= 20. El estado inicial de los qubits está definido por  = (1, -0.9,0.9)
= (1, -0.9,0.9)

Figura 3 Dinámica de las correlaciones con interacción bifotónica, con pérdidas de fotones: (a) unifotónicas y (b) bifotónicas. concurrencia (negro), discordia (rojo). El número promedio de fotones térmicos  = 20. El estado inicial de los qubits está definido por
= 20. El estado inicial de los qubits está definido por  = (1, -0.9, 0.9)
= (1, -0.9, 0.9)
En las figuras 2(a-b) se observa el efecto de congelamiento, durante períodos de tiempos finitos, de la discordia cuántica con la dinámica unifotónica (figura 2 a) y bifotónica (figura 2 b) sin pérdidas.
Este efecto es similar al que se obtuvo en [3] donde consideran interacción unifotónica. La evolución de la concurrencia (línea de color negro discontinua) es periódica pero se mantiene constante en lapsos de tiempos cortos, indicando que los qubits se encuentran entrelazados de forma constante en esos intervalos de tiempo. Para la dinámica unifotónica (figura 2 a) el ancho de tiempo de congelamiento de las correlaciones es más grande que en la dinámica bifotónica (figura 2 b). Sin embargo, cuando en nuestro sistema se consideran pérdidas unifotónicas o bifotónicas hacia el reservorio desde las cavidades, la amplitud disminuye tanto para la discordia como para en entrelazamiento como se muestra en la figura 3.
Los resultados de las figuras 3(a-b) evidencian el efecto de congelamiento de la discordia para la evolución temprana del sistema, sin embargo, por la decoherencia el efecto desaparece, llevando la discordia a un valor casi-estacionario por un tiempo finito y seguramente en un tiempo suficiente largo ésta correlación convergerá a cero. La concurrencia (línea de color negro discontinua) con pérdidas unifotónicas (figura 3 a) muere y nace súbitamente en diferentes instantes de su evolución hasta que muere definitivamente en el tiempo en que la discordia oscila cercano de un valor finito. Cuando se consideran pérdidas bifotónicas (figura 3 b) la concurrencia disminuye su amplitud a medida que transcurre el tiempo hasta que se hace cero en el resto de su evolución. Es decir, los qubits logran estar más tiempo entrelazados cuando consideramos la dinámica con pérdidas bifotónicas antes de tener una muerte súbita.
5. Conclusiones
Se calcularon y se analizaron las correlaciones cuánticas con dinámica unifotónica y bifotónica sin pérdidas y se observó el efecto de congelamiento de la discordia cuántica, similar al que obtienen en [3], para otro modelo con dinámica unifotónica. Este efecto se manifiesta también para la dinámica bifo-tónica que puede ser útil para algunas aplicaciones que impliquen procesos multifotónicos. Cuando se tienen en cuanta las pérdidas unifotónica y bifotó-nicas el efecto de congelamiento se presenta para la evolución temprana del sistema y debido la de coherencia el efecto desaparece. De acuerdo a los resultados de la Fig. 3 la concurrencia con interacción y pérdidas bifotonicas, no evidencia efectos de muerte y nacimientos súbitos durante su evolución oscilatoria. La demostración del efecto de congelamiento de la discordia es de utilidad potencial para realizar el procesamiento de la información cuántica, por ejemplo, diseñar sistemas cuánticos para preservar las correlaciones cuánticas durante un tiempo finito.
























