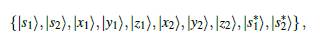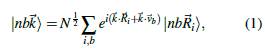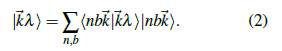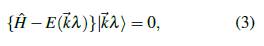1 Introducción

Los compuestos GaAs y AlAs se utilizan en la actualidad para fabricar dispositivos tales como circuitos integrados a frecuencias de emisión infrarroja, diodos y celdas fotovoltaicas. Además, se utilizan en la producción de láseres de baja potencia con aplicación en medicina, especialmente en odontología.

Se han reportado algunos estudios teóricos, usando la teoría del funcional densidad (DFT), sobre las propiedades estructurales, transiciones de fase estructurales y propiedades electrónicas [¹, ², ³,⁴]. También se pueden encontrar en la literatura trabajos experimentales sobre la determinación de los gaps de energías prohibidas [⁵, ⁶, ⁷, ⁸, ⁹].

El cálculo de estructura electrónica usando esquemas Tight-Binding (TB) con menos de ocho bandas no describe adecuadamente semiconductores con enlace covalente. Por ejemplo, en cristales tipo diamante y Zinc-Blenda (ZB), con enlace sp³, es necesario al menos cuatro orbitales para cada átomo: un orbital s y tres p, que originarían una matriz Hamiltoniana 8 x 8 [¹⁰, ¹¹, ¹², ¹³]. Este modelo suministra un esquema simple para describir bandas de valencia (BV).

Los intentos de describir las bandas de conducción (BC), en semiconductores, con esquemas TB sp³ a primeros vecinos más cercanos han fallado; por ejemplo, Chadi et al. [¹⁴] mostró que con la base sp³ no se obtienen los gaps indirectos en semiconductores tipo diamante y ZB como Si, Ge, AlAs o GaP. La causa principal de esta falla es que se omite el uso de estados excitados, tales como los d. Sin embargo, un esquema TB sp³d⁵ para semiconductores diamante o ZB implicaría usar una base de nueve orbitales por átomo: un orbital s, tres p y cinco orbitales d y por tanto, una matriz Hamiltoniana 18 x 18.

En este trabajo se propone usar un Hamiltoniano TB en la base sp³s*, en la que se incluyen los estados excitados s*. Estos últimos tienen las mismas propiedades de simetría de los estados s y con ellos se consigue reemplazar los estados d, disminuyendo la dimensión de la matriz Hamiltoniana de 18 x 18, en la base sp³d⁵, a 10 x 10 (un orbital s, tres p y un orbital s^* por átomo). Además, usando los estados s*, se reproducen adecuadamente los gaps indirectos de los materiales semiconductores en los que la base sp³ falla.

El artículo está organizado de la siguiente manera, en la Sección 2, se proporciona una breve descripción de la estructura cristalina y el marco teórico necesario para realizar los cálculos. En la Sección 3, se presentan los resultados y su discusión. Finalmente, en la Sección 4 presentamos las conclusiones del trabajo.

2 Modelo Teórico

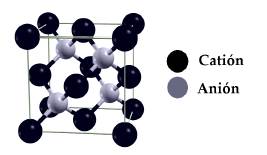
Consideramos que los compuestos estudiados cristalizan en la estructura tipo ZB, mostrada en la Figura 1. La celda unitaria convencional consiste de dos celdas cúbicas centradas en la cara (FCC) desplazadas un cuarto de la diagonal principal una respecto a la otra. El catión (Ga o Al) se ubica en una de las celdas FCC y el anión (As) en la otra celda FCC [¹⁵].

Figura 1 Celda unitaria convencional de la estructura cristalina tipo ZB. 

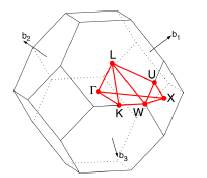
La primera zona de Brillouin (PZB) se muestra en la Figura 2 [¹⁶], en la que se han indicado algunos puntos y caminos de alta simetría.

Figura 2 PZB de la estructura ZB. 

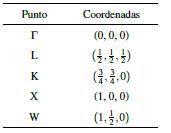
Las coordenadas de los puntos de alta simetría, en unidades de 2π/α _L (α _L es la constante de red) se muestran en la Tabla 1.

Tabla 1 Puntos de alta simetría en la PZB, en unidades de 2 π / α _L  

La base de estados, en la que se construye la representación matricial del operador Hamiltoniano, se escoge a partir de las distribuciones electrónicas de los átomos aislados. Las distribuciones electrónicas del Ga, As y Al son, respectivamente, 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p¹, 1s²2s²2 p⁶3s²3 p⁶3d ¹⁰4s²4 p³, 1s²2s²2 p⁶3s²3 p¹.

Según el método TB, se trabaja con orbitales de valencia: 4s y 4p para Ga y As, y 3s y 3p para Al, estos conformarán la BV en el sólido. Para la BC se deberían incluir los orbitales 4d del Ga y As y los 3d del Al; existen cinco orbitales d, aumentando el número de elementos de la base. Para evitar esto se prefiere trabajar con un orbital excitado s*, con simetría tipo s. Este nuevo orbital hace las veces de los orbitales d, sin que los cambios sean significativos, en lo que respecta a la BV y la parte inferior de la BC. De esta manera la base de estados atómicos será,

donde los subíndices 1 y 2 se usan para diferenciar cada átomo. Teniendo en cuenta esto, la matriz Hamiltoniana tendrá una dimensión de 10 x 10 [¹⁷].

Para construir la matriz Hamiltoniana usamos una base de orbitales de Löwdin (orbitales atómicos simétricamente ortogonalizados)

donde n = s, p, s*; b = a, c es un índice de sitio (a para el anión y c para el catión); 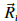_i corresponde a posiciones del anión; 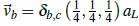establece la posición de los cuatro cationes más cercanos a un anión, δ _b , _c es la delta de Kronecker; y los N vectores de onda 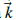se encuentran en la PZB.

Los estados de Bloch, construidos en la base de orbitales de Löwdin son de la forma,

En la ecuación (2), λ es un índice que especifica cada banda y, de acuerdo al número de estados de la base, puede tomar 10 valores.

Entonces, los valores de energía 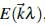, soluciones de la ecuación de Schrödinger

se determinan, para cada valor de λ, a lo largo de los caminos de alta simetría de la PZB indicados en la Figura 2 y en la Tabla 1.

3 Resultados y Discusión

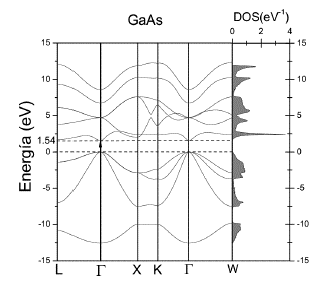
En las Figuras 3 y 4 se muestra, a la izquierda, las relaciones de dispersión (energía en función del vector de onda) para el GaAs y AlAs a lo largo de algunos caminos de alta simetría de la PZB.

Figura 3 Relaciones de dispersión y DOS total para el GaAs. 

Figura 4 Relaciones de dispersión y DOS total para el AlAs. 

En estas figuras, el cero de energías se ubica en el borde superior de la BV (energías negativas). Se observa que, en las relaciones de dispersión de GaAs, el máximo de BV se encuentra en el punto Γ y corresponde a un triplete, el ancho de la BV es de ~ 12.54 eV.

En la Tabla 2, se presentan algunos valores teóricos y experimentales del gap para cada compuesto. Se puede observar que los valores obtenidos en nuestro trabajo, comparados con métodos teóricos más sofisticados (que usan bases de orbitales más grandes y complejas) y con trabajos experimentales, coinciden bastante bien. Adicionalmente, podríamos mencionar que las diferencias más significativas entre nuestras relaciones de dispersión y las calculadas por otros métodos, como el de la teoría del funcional densidad (DFT), aparecerán en la parte superior de la BC; esto se debe a que no utilizamos los orbitales d sino otros orbitales que tienen simetría tipo s (los orbitales s*).

Tabla 2  Comparación de nuestros valores del gap (en eV) con otros trabajos experimentales y teóricos 

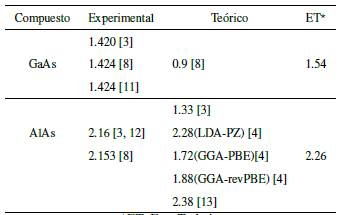
*ET: Este Trabajo.

La BV está formada por las cuatro primeras bandas (entre ~-12.54 eV y 0 eV). Si se recorren los caminos L - Γ y Γ - X solo se distinguen tres bandas, esto significa que alguna de ellas es un doblete. En los caminos X - K, K - Γ y Γ - W se notan claramente las cuatro bandas, implicando que estos son caminos menos simétricos que los dos primeros. La BV coincide bastante bien con la encontrada en otros trabajos [1,3,4]. Reproducimos el gap de energías prohibidas directo en el punto Γ. El valor encontrado en nuestro trabajo es ~ 1.54 eV.

En la Figura 3, a la derecha, también se muestra la densidad de estados total (DOS) calculada en toda la PZB. En el eje vertical se encuentran las energías y en el eje horizontal la DOS (en estados/eV^-1). El valor de la integral de esta DOS calculada desde - ∞ hasta 0 es igual a cuatro, que corresponde al número de estados de la BV, y el valor total de la integral calculada de - ∞ hasta + ∞ es igual a diez, que corresponde al número de estados totales considerados. Esta gráfica, confirma los resultados obtenidos para las relaciones de dispersión: se obtiene un gap de ~ 1.54 eV y el ancho de las BV y BC coinciden.

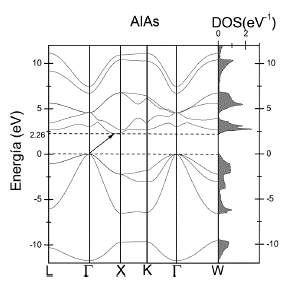
Para el caso de AlAs, la Figura 4 muestra que el gap es indirecto entre el punto Γ y un punto en el camino Γ - X, indicado con una flecha. El valor encontrado para el gap es ~ 2.26 eV. Al igual que en el GaAs, el punto Γ es triplemente degenerado.

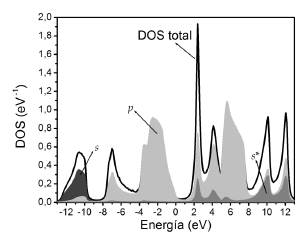
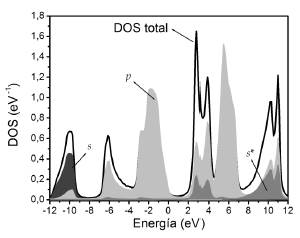
En las Figuras 5 y 6 se presentan las DOS totales y parciales para el GaAs y AlAs.

Figura 5 DOS total y parciales para el GaAs. 

Figura 6 DOS total y parciales para el AlAs. 

Se nota que los orbitales s se encuentran tanto en la BV como en la BC, con una contribución más significativa en la BV. En la BV se encuentran mayoritariamente en la parte inferior y son aportados en su mayoría por el anión.

En la BC se encuentran en su mayoría en la parte inferior y el aporte más significativo es debido al catión. Se observa que los orbitales p están presentes tanto en la BV como en la BC. En la BV se tiene un aporte mayoritario de los orbitales p del anión sobre toda la banda, mientras que la contribución del catión se encuentran en la parte superior. En la BC se observa un aporte mayoritario de orbitales p del anión en la parte inferior de la banda, mientras que en la parte superior predominan los orbitales p del catión. Finalmente, la discriminación de orbitales s*, como era de esperarse, muestra que éstos se encuentran en su mayoría en la BC ya que en nuestra base corresponden a estados excitados.

4 Conclusiones

Hemos calculado las relaciones de dispersión y DOS totales y parciales de los compuestos GaAs y AlAs usando un Hamiltoniano TB sp ³ s ^* . La modificación del Hamiltoniano TB usando orbitales s* en lugar de orbitales d simplifica los cálculos y permite encontrar resultados bastante cercanos a los reportados en otros trabajos. Nuestro método, aunque es más sencillo que los métodos basados en DFT, reproduce bastante bien la BV, el gap de energías prohibidas y la parte inferior de la BC.