Introduction
One of the areas that significantly impacts society is education, as it has a great influence on reducing poverty and unemployment, as well as on improving the life conditions of the community 1. In the education sector, metrics have been identified such as the annual dropout rate, the dropout rate per cohort, the graduation rate, and the inter-monthly absence rate 2, which allow measuring students’ academic performance 3. Academic performance is a multidimensional concept that depends on multiple aspects such as the objectives of the teacher, the institution, and the student, etc. It also requires an integration of different techniques and methodologies for its prediction 4.
Academic performance involves each of the actors in the teaching-learning process, which has been approached from different fields of knowledge (psychology, education, medicine, statistics, among others), issuing various definitions 5), (6. This concept is considered to represent a level of knowledge demonstrated in an area or subject while considering age and academic level 7. In other words, academic performance is measurable from an assessment of the student; it is the sum of different and complex factors that generate an impact on him/her 8. Similarly, for 9, there are a series of factors that revolve around effort and indicate the success or failure of the student 10. Currently, with the incursion of the web and ICTs applied to education, this has undergone a series of changes, among which a large volume of data has emerged given the interaction between students, teachers, and institutions 11), (12. These data are stored, and little of them is used to improve the academic performance and orientation of the student 13. Therefore, it is necessary to investigate a decision-making model that contributes to the improvement of academic performance.
Decision-making models in the education sector have undergone a certain evolution in terms of the type of data analytics used, as suggested by 14: descriptive analytics (performance of all the activities studied) carried out with spreadsheets; diagnostic analytics (past performance to analyze information) conducted by means of computer science; and predictive analytics (anticipating behaviors based on historical relationships between variables) performed using data mining and machine learning techniques.
Related works
Machine learning is a subdiscipline of artificial intelligence that is based on addressing and solving problems from numerical disciplines such as probabilistic reasoning, research based on statistics, information retrieval, and pattern recognition. In this way, machines, through the execution of algorithms, become capable of performing tasks commonly performed by humans 15. This field is subdivided into several branches, as shown in Fig. 1. Supervised learning takes place when each of the observations of the data set has a related variable or information that indicates what happened (i.e., when entries are labeled). Machine learning (ML) has begun to permeate the educational field, allowing for the collection, cleaning, analysis, and visualization of data on educational actors, in order to optimize related aspects of the teaching-learning process 15, which is why it is currently regarded as one of the techniques that will help decision-making in these contexts 16.
In the last decade, multiple studies have been carried out which seek to establish the variables that specifically affect academic performance. Research has been carried out in areas such as psychology, where, apart from demographic data, the influence of variables related to interest, motivation, attendance, integration, self-regulation, commitment, participation, anxiety, and communication on academic performance have been considered 17)-(21. From the field of statistics, contributions have been made such as those reflected in 21)-(23, which apply statistical models that seek to examine the variables involved in university admission (admission and pre-university exams), proposing a model that involves various interrelated variables in an attempt to predict academic performance. Some early research have grouped the variables into economic, demographic, and psychological factors 24), (25. Others have expanded the number of factors, grouping them into demographic, socioeconomic, institutional, sociocultural, socioeconomic, pedagogical, academic, psychological, intellectual, and technological factors, and, due to the rise of ICTs, they have included the learning analytics factor (online interactions) 10.
Recent works have made it possible to group the variables into fewer factors, such as previous academic performance, demographics, e-learning activity, and psychological and environmental factors 26, considering their influence on the variable under study. Table I shows some previous works that have used supervised algorithms as prediction models of academic performance. The variables associated with these studies were grouped into the factors of the classification proposed in 27. This classification is obtained considering previous research and our reference research 27)-(29, grouping the variables that are easy to identify, of a controllable nature, that are supported by theory, and that can be grouped into previously defined factors. It can be seen that most variables are grouped mainly within the academic and sociodemographic factors (place of residence, number of family members, level of education of the parents, distance traveled to the educational center), followed by psychosocial factors and academic management.
Table I Previous work on predicting academic performance using supervised algorithms
| Factor | Variables | Previous work with supervised machine learning algorithms |
|---|---|---|
| Academic | Government test score, grade point average from the last year of high school, admission test result, academic average or GPA (Grade point average), grades by subject, behavior in seminars, conferences and extracurricular activities | (30-40) |
| Socio - demographic | Age, gender, language, marital status, nationality, socioeconomic variables such as stratum, family income, place of residence, parental education level, occupation, number of family members, distance traveled per journey to school | (32-36,41-45) |
| Online learning | Number of times of entry to the platform, number of tasks assigned by the teacher, number of exams taken, participation in the discussion forum, amount of material viewed, hours online, number of attendances or absences. | (2, 46-48) |
| Academic management | Year of admission to the university, number of credits, scholarships obtained, credits taken, credits approved, credits lost, final grade for each subject, number of subjects taken, number of subjects passed, number of subjects missed, number of subjects repeated and number of times he has missed a subject. | (27,37,39,40,45-47,49) |
| Psychosocial | Interest, motivation, assistance, integration, teamwork, self-regulation, commitment, participation, stress, anxiety | (30,34,38,46,47,50-53) |
| Academic environment | Type of class / course, duration of the semester, type of program, duration of classes, faculty, course preparation, material, assignments, available resources. | (46,48,49,53,54) |
Contributions and organization
This work explores three concepts that converge in the models: academic performance and its possible ways of evaluating it; the factors that affect it; and supervised machine learning algorithms. In the literature review in 27-29, which was previously published by the authors, there are related works that propose models with several variables that influence performance, but these are usually applied to studying academic performance in an exam, in a specific course, in a year, or to obtain an academic degree. In this sense, this research addresses the problem of determining it throughout the student’s academic life (ten academic semesters) by using data transformation tools, feature selection methods, and supervised ML algorithms.
The fields or areas of knowledge that have studied the multidimensional variable of academic performance are diverse. This has been approached from the field of psychology 17)-(19), (55)-(57, which has applied tools related to questionnaires on students’ perceptions regarding academic performance, followed mainly by statistical tools that have a much more marked focus on demographic data and their influence on the variable of interest 21), (22), (58), (59. Likewise, research related to data science is important, especially studies that use data mining algorithms and ML applied to the field of education.
Therefore, a significant contribution is to propose a methodology and a model to establish university academic performance. Approximately 324 variables are analyzed in this work (50 variables analyzed for each academic semester). The authors provide the essential steps to be followed in order to correctly apply ML algorithms to the field of education (in this case, for a 10-semester engineering program). The results show that, with a good dataset, it is possible to analyze situations of academic life or indicators of educational quality that lead to an improvement of the educational process at the university and secondary and primary education levels. This is an interesting contribution for teachers and researchers in the field of education and engineering who wish to investigate issues of education and ML, since engineering articles generally do not provide a clear and easy-to-learn methodology.
Using ML algorithms (Decision Trees, KNN, SVC, Naive Bayes, LDA), various models have proposed in order to predict the academic performance of engineering students in each of their 10 academic semesters. The number of records used to analyze the 50 variables on average in each of the 10 semesters ranges between 2.300 and 2.100 for the first four semesters studied, as well as between 2.100 and 1.800 for the other semesters. These proposed models and their relevant variables allow for decision-making regarding both students and teachers. This, despite the fact that all of the variables present in the consulted literature are not used.
The rest of the article is organized as follows: Section 2 describes the research methodology; Section 3 details the tests and their results; Section 4 presents a discussion of the results obtained; and Section 5 outlines the conclusions.
Materials and methods
The methodology employed in this research is presented in the following eight steps: 1) referential information; 2) data source; 3) data cleaning and conditioning; 4) statistics; 5) data transformation; 6) selection of characteristics; 7) prediction algorithms; and 8) performance metrics.
Reference information
Initially, a review was carried out in databases such as Springer Links, Proquest, IEEE Explorer, and Science Direct, using combinations of keywords, i.e., “academic performance + machine learning, supervised learning + academic performance, academic performance + EDM, data mining + academic performance, improving educational + Machine Learning”. The aim was to identify the supervised learning ML algorithms for evaluating academic performance in higher education along with its relevant variables. This referential research was carried out for a period of five years using the method for systematic literature reviews (SRL) proposed by 60, whose initial phase has already been published 61.
Data source
Universidad Distrital Francisco José de Caldas (Bogotá DC, Colombia) provided a database with a total of 1.614.472 data from 4.738 students of the Industrial and Electrical Engineering programs between 2008 and 2018. These data from both teachers and students are summarized in 324 variables and grouped into five factors defined in Table I: pre-university academic, socio-demographic, socio-economic, academic management, and academic environment. Based on this information, a methodology was proposed, as well as supervised algorithms that allow predicting university academic performance.
Data cleaning and conditioning
This process initially consisted of eliminating unwanted observations, correcting structural errors, managing values, and handling missing data, as this would probably be reflected as abnormal data and cause poor prediction in the final models. Likewise, information from students who had inconsistent records was discarded, and new variables were created from the information provided (e.g., distance traveled per journey to school, per-semester average, number of subjects taken). Thus, the information was organized, considering the aforementioned factors and the vast majority of variables that group each factor, which resulted in 4.500 records of undergraduate students.
Data statistics
The supplied datasets (.CSV files) were merged, thus obtaining input data. Descriptive statistics were carried out through Python libraries in order to learn more about the data framework 62.
Data transformation
As it is possible that an independent variable exerts a greater influence on the dependent variable (in this case, academic performance) due to the fact that its numerical scale is greater than that of the other variables, it was necessary to carry out different types of transformations in order to obtain a better quasi-Gaussian curve for the variables of the dataset (Rescale, Standardize, Normalize, Yeo-Johnson, Box-cox). These transformations sought to eliminate influence effects, since they are mainly syntactic modifications carried out on data without changing the algorithm 63.
Feature selection
In order to take advantage of the information provided, a good selection must be made of the most inclusive or relevant characteristics of the output variable (64). The literature presents two options: the use of feature selection methods (which include and exclude the most relevant features for the development of the problem without changing them and which are generally divided into filter, wrapping, embedded, and assembly methods); and dimensional reduction methods (which create new combinations of attributes from base ones).
Prediction algorithms
The supervised machine learning algorithms implemented in the dataset were KNN, Decision Trees, SVC, Naive Bayes, and LDA. It is worth mentioning that it was necessary to calculate the dependent variable of study (academic performance) semester by semester in accordance with the norms established by the University and the Colombian government, since its wide range of numerical values generated inconsistencies in the execution. The scale generated to define the variable is shown in Table II, which is based on the ranges established by the Colombian Ministry of National Education.
Table II Performance variable conventions
| Performance | Average | Number |
|---|---|---|
| Superior Performance | 50 - 45 | 4 |
| High performance | 44 - 40 | 3 |
| Basic Performance | 39 - 30 | 2 |
| Low performance | 29 - 0 | 1 |
K-Nearest Neighbors (KNN) is one of the classification algorithms whose performance depends on the selection of the hyper parameter K and the distance measure used between two data points (Euclidean, Manhattan, or Minkowski) 65. Decision Trees are a kind of diagram that consists of internal nodes corresponding to a logical test on an attribute and connection branches used to illustrate the whole process and show the result 66. The top node in a tree is the root node and represents the entire dataset 67. In order to establish which is the best partition of the node, different metaheuristics have been suggested which seek to minimize entropy, i.e., information gain and the Gini index. SVM (Support Vector Machines) allow searching for a hyperplane in a high dimensional space that separates the classes in a dataset. It is implemented using a kernel (linear or nonlinear) 68. Naive Bayes is a classifier supported by Bayes’ theorem with good classification precision. It is implemented by estimating a posterior probability 69. Finally, LDA makes predictions by estimating the probability that a new set of entries belongs to each class. The class that gets the highest probability is the output class, and a prediction is thus made 70.
Performance metrics
There are several ways to evaluate the results of a ML algorithm. According to 71, the quality of the classification should be evaluated by one of the four different performance metrics: accuracy, precision (specificity), recall (sensitivity), and the F1 score. These values are are determined from the confusion matrix (Table III).
Table III Confusion matrix
| Predicted Values | ||||
| Positive | Negative | |||
| Actual Values | Positive | True Positive (TP) | False Negative (FN) | |
| Negative | False Positive (FP) | True Negative (TN) | ||
Accuracy is defined as the number of correctly predicted instances over the total number of records, precision is the ratio of correctly predicted positive instances to the total predicted positive instances, sensitivity is calculated as the ratio of the number of correctly predicted instances to the total number of positives, and the F1 score is the weighted average of precision and sensitivity.
Results
By applying the methodology described above, various results were obtained for steps 4, 5, 6, 7, and 8.
Regarding statistics
The base dataset consists of 324 variables on average which influence students’ academic performance and were grouped by semester. It was necessary to create other variables mentioned in the literature that could influence performance, e.g., the number of subjects taken, missed, and repeated. Universidad Distrital Francisco José de Caldas constantly measures the variables of interest and commitment of the students during their time at the university, applying measurement mechanisms per semester (known as academic tests). Another variable created was distance. This variable is considered, since the time it takes for the student to go from his residence to the university can influence his/her academic performance. The distance between the student’s residence and the university was determined by means of approximations using the Google Maps tool, drawing a radial perimeter, and taking the centroid of each location on the map of Bogotá as a reference.
Data transformation
Data transformations are used to change the type or distribution of data variables towards a standard range, so that they can be compared and subjected to different correlation and/or prediction models 72. From the 4.500 student records, different types of data transformations were carried out, since it is often possible to improve the performance of a range of ML algorithms when the input characteristics are close to a normal distribution 73 or are quasi-Gaussian (Fig. 2a). As an example, Fig. 2b depicts the curves of how the performance of the models (KNN, Decision Trees, NB, and SVC) varies with and without a transformation method in the context under study. The performance metric used to compare the results of each model is accuracy. Fig. 2b compares the model performance improvement when using data without transformation (NO_TRANS) vs. using data transformation methods (Rescale, Standardize, Normalization, Robust Standardization, Box-Cox, or Yeo-Johnson) on the implemented supervised algorithms. The improvement in accuracy typically ranges from 3 to 7% when a transformation method is applied to the data. This is not the case for the SVC algorithm with non-linear kernel. The best results are obtained when the Yeo-Johnson transformation is used.
Feature selection
It was interesting to determine, for each academic semester, which would be the most influential variables in a student’s performance as he/she advances through his/her university life. To this effect, filter methods were used (Pearson correlation, ANOVA, Chi Square, and mutual information), as well as envelope methods (recursive feature elimination RFE with logistic regression, RFE with logistic regression, RFE-SVC, RFE-Linear regression, RFE-Decision Trees, Backward Selection, Forward Selection, Bi-Directional Elimination), embedded methods (linear regression, Lasso regularization), and assembly methods (CART, Random Forest, ExtraTreesClassifier, XGBoost, CatBoost, LightGBM). The number of characteristics that yielded the best per-semester value of the performance metric in the models for Industrial Engineering is shown in Fig. 3a. It is worth mentioning that the results obtained by each method in each of the semesters were tabulated and, in general, the characteristics produced by the assembly methods are the ones that provide the best results when the supervised learning algorithms (KNN and Decision Trees) are applied. This step is considered fundamental for the models, as it is necessary for those that provide information to the model to be the relevant variables, not those that introduce noise. As an example, Fig. 3b shows the results regarding the precision of the models involving Decision Trees and KNN when trying to predict academic performance in the sixth semester of Industrial Engineering with different amounts of characteristics while using 10-fold cross-validation. In a previous work, the authors had presented a first attempt to predict the academic performance of students in only the first semester, with a model precision of 66,6 %, in which they established the pre-university variables that influenced the academic performance of students (10 out of 25 were selected) 74.

Figure 3 a) Number of best characteristics to predict academic performance in each semester; b) accuracy according to the number of best variables selected by the methods
Another interesting aspect was the fact that engineering courses usually have a common component (basic engineering subjects). Therefore, this study sought to identify which would be the subjects of this basic component that most influence the determination of university academic performance when estimated consecutively for the first three semesters (Table IV).
Table IV Common variables in the determination of academic performance within the basic cycle of Industrial and Electrical Engineering
| Semester | Common variables | |
|---|---|---|
| 1 | ICFES Global Score ICFES Area of Biology ICFES Math Area | ICFES Area of Biology School Location Residence Location |
| 2 | ICFES Global Score ICFES Math Area ICFES Area of Biology Residence Location | Student Average (1 Semester) Note_Catedra FJC Number of Subjects Repeated (1 Semester) Note_Text |
| 3 | Student Average (1 Semester) Student Average (2 Semester) Note Differential Calculation Number of Credits Studied (2 Semester) | Note Algebra Number of Subjects Studied (2 Semester) Number of Subjects Approved (1 Semester) Note_Integral Calculation |
Prediction algorithms
As previously mentioned, models with supervised learning algorithms were implemented: SVC, KNN, Decision Trees, Naive Bayes, and LDA for the dataset corresponding to each of the 10 academic semesters, which had to be divided into training and test data. The literature presents options in order to avoid subsampling or oversamplings such as cross-validation (it works in the search for less variance), which works by dividing the data set into k parts (k = 10), which are called folds (i.e.,10-fold), where the first fold will act as a validation set and the model is trained with the k-1 (fold). Each time the model is validated with a different fold, it will be trained with the remaining k-1. In addition, the random method was used (70% for training data, 30% for the test data) in order to estimate the performance of the algorithms 73. Some of the best results of the performance metrics of the algorithms are shown in Table V for Industrial Engineering.
Table V Results of the models with cross-validation (CV) and random method (for different semesters)
| Accuracy | Cross Validation Method - Training data | Cross Validation Method - Test data | Random Method - Training Data | Random Method - Test Data | Accuracy | Cross Validation Method - Training data | Cross Validation Method - Test data | Random Method - Training Data | Random Method - Test Data | |
|---|---|---|---|---|---|---|---|---|---|---|
| SEMESTER 1 | SEMESTER 6 | |||||||||
| KNN | 0,615 | 0,616 | 0,660 | 0,602 | KNN | 0,836 | 0,817 | 0,811 | 0,806 | |
| SVC | 0,534 | 0,513 | 0,626 | 0,637 | SVC | 0,773 | 0,770 | 0,705 | 0,235 | |
| D_TREE | 0,639 | 0,637 | 0,634 | 0,621 | ARBOL | 0,805 | 0,765 | 0,821 | 0,789 | |
| NAIVE BAYES | 0,582 | 0,623 | 0,609 | 0,607 | NAIVE BAYES | 0,685 | 0,730 | 0,692 | 0,660 | |
| LDA | 0,628 | 0,638 | 0,627 | 0,642 | LDA | 0,812 | 0,806 | 0,810 | 0,820 | |
| SEMESTER 2 | SEMESTER 7 | |||||||||
| KNN | 0,815 | 0,779 | 0,836 | 0,810 | KNN | 0,804 | 0,7339 | 0,782 | 0,761 | |
| SVC | 0,590 | 0,425 | 0,710 | 0,670 | SVC | 0,703 | 0,634 | 0,645 | 0,687 | |
| D_TREE | 0,817 | 0,736 | 0,847 | 0,766 | ARBOL | 0,820 | 0,710 | 0,777 | 0,681 | |
| NAIVE BAYES | 0,670 | 0,676 | 0,674 | 0,679 | NAIVE BAYES | 0,669 | 0,608 | 0,690 | 0,650 | |
| LDA | 0,805 | 0,771 | 0,810 | 0,764 | LDA | 0,776 | 0,743 | 0,787 | 0,757 | |
| SEMESTER 3 | SEMESTER 8 | |||||||||
| KNN | 0,782 | 0,785 | 0,766 | 0,792 | KNN | 0,766 | 0,7075 | 0,776 | 0,746 | |
| SVC | 0,607 | 0,709 | 0,597 | 0,660 | SVC | 0,664 | 0,6126 | 0,637 | 0,603 | |
| D_TREE | 0,782 | 0,762 | 0,808 | 0,782 | ARBOL | 0,791 | 0,669 | 0,757 | 0,692 | |
| NAIVE BAYES | 0,606 | 0,661 | 0,615 | 0,644 | NAIVE BAYES | 0,615 | 0,5039 | 0,598 | 0,510 | |
| LDA | 0,783 | 0,785 | 0,7838 | 0,776 | LDA | 0,763 | 0,7108 | 0,769 | 0,7301 | |
There are different libraries that are used to optimize the hyperparameters of the classification algorithms, such as Scikit-learn (GridSearch, Random Search), and Scikit-Optimize. In this work, the optimization of parameters was carried out by means of Grid Search, an approach that is in charge of constructing and exhaustively checking all the combinations in the parameter space (specified in advance) of an algorithm. To determine the best value for the hyperparameters, the cross-validation method was used to avoid over-fitting the model. Some hyperparameters that should have been optimized for each of the models are shown in Table VI.
Performance metrics
There are different metrics to determine if a model performs well. Fig. 4a shows the value of the accuracy metric of each model for each of the academic semesters after implementing the Yeo-Johnson transformation (it was the one that yielded the best, quasi-Gaussian data) and selecting the most influential characteristics in the response variable (academic performance). An accuracy value (ratio between the correctly predicted observation and the total number of observations) close to 1 indicates that all the predictions are correct. A value close to 0 suggests a very bad prediction model. The KNN algorithm yielded the best results in the vast majority of academic semesters (greater than 77,5 %), closely followed by the Decision Trees (greater than 76,9 %) and the LDA method (greater than 76,5 %). The KNN algorithm was not only the best at predicting academic performance in each semester; it also showed precision values between 76 and 82% when evaluating the students’ year of study (every other semester). This is a contribution of this work, in the sense that previous works show predictions for a group of data in particular that correspond to a subject, several subjects of a semester, or, in the best of cases, to a sum of semesters in particular. Instead, this research aimed to predict academic performance throughout students’ academic life, i.e., semester after semester and year after year in different engineering curricular programs (Fig. 4b).
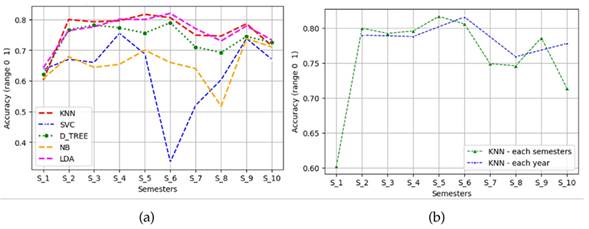
Figure 4 a) Summary of evaluation metrics of classic ML models with supervised learning (industrial engineering); b) KNN precision in predicting academic performance (per semester and per year for industrial engineering)
The best variables considered to predict academic performance in each of the semesters are shown in Table VII. As expected, there are differences between the predictions made for each semester and those for each year.
Table VII Relevant variables by academic semester to determine academic performance (four semesters)

There are different metrics to evaluate the algorithms. As an example, it is shown in Table VIII that the KNN algorithm not only obtained high accuracy results, but it also surpassed the others in precision, recall, and the F1 score. Precision values (which measure the ability of a classifier not to label an observation as positive when it should be considered as negative) are close to those of accuracy. The recall and F1 scores are also good values, as they are close to 1 (100 %)
Table VIII Metrics of the algorithms implemented for the first four academic semesters (industrial engineering)

Then, the supervised algorithms were implemented. Note that the best features were provided and that the hyperparameters were optimized by implementing the Grid Search method. Fig. 5 shows the average results regarding the precision metric for predicting academic performance in Industrial and Electrical Engineering programs.
Discussion
Based on the results obtained, it can be stated that, in the last decade, the development of tools and techniques in the field of computer science has allowed data analytics to penetrate many fields, such as the education sector, where it is used not only in the prediction of students’ academic performance but also of other indicators of educational quality such as dropout and graduation rates. Thus, this project lays the foundations to continue with the exploration of how to estimate, predict, or group students in order to take appropriate actions that guide their academic course. The characteristics selection methods employed show that the gender variable was not relevant when determining academic performance, which is somewhat similar to the findings of studies such as 75 and 75. However, when reviewing the literature, works from the field of psychology were found, such as 76, 77, and 78, which state the opposite. Something similar occurs with the place of origin, as studies such as 78 and 79 argue that students from diverse geographic locations have specific knowledge, prior experiences, and different ways of life that are guided in various ways by teachers to meet educational needs, which affects the way they learn. However, there are studies such as 80 and 81 which suggest that this has no significant effect. Thus, it seems that, depending on the analyzed group, the results may or may not be similar in terms of the influence of the independent variables on academic performance, which happened in this work.
The academic average or GPA (grade point average) is one of the variables that exerts the most influence on the determination of performance, albeit not in all 10 semesters, as there are semesters where performance is influenced by the number of subjects taken and their corresponding grades. Socioeconomic variables do not show a high influence on the precision of the prediction for first semester students, unlike the results obtained by 82. Also for first semester students, 40 achieved 49,078% accuracy with their best algorithm; in this work, this value was between 60 and 65 %. The performance of the algorithms yielded better values, despite being similar to those implemented by 35), (52), (83, and 84. Nevertheless, the results of this work are very different to those of 38 with regard to the SVC algorithm; the latter obtained values close to 90 %, whereas our study was below 80 %. It is worth mentioning that 38 considered psychological parameters, learning strategies, and learning approaches that were not taken into account in this work. This suggests that the determination of academic performance is a complex process that varies from institution to institution, and that it may not be possible to generalize with regard to the influencing variables and the best algorithms. It is instead possible to estimate according to particular conditions while considering general variables and factors. According to the results, the KNN algorithm allows predicting, with metrics such as accuracy, the per-semester or yearly academic performance of a student while only considering some academic variables (subjects attended, averages, subjects failed and approved, and overall approved credits) and some pre-university demographic variables.
However, this study has some methodological limitations, such as the lack of available and/or reliable data. The date used in this research is the product of the information provided by the systems office of Universidad Distrital Francisco José de Caldas (data warehouse), to which a generous cleaning process should have been applied in light of the errors found. Another important limitation is access to information, since some information related to economic and psychosocial variables was not provided by the University (it was regarded as private information). Therefore, some variables such as commitment, participation, stress, anxiety, assertive communication, and family income could not be analyzed in order to determine whether or not they influenced the academic performance of the students. These limitations could be corrected by means of a database that allows access to as many variables as possible, as well as investigating variables of the students’ environment which may influence their performance.
Conclusions
According to the work presented and the results obtained, the following main conclusions can be drawn:
Not applying transformation or feature selection methods on the data generates models with low performance metrics, even when the hyperparameters of the supervised learning algorithms are optimized. This is reflected in the good results obtained with the Yeo-Johnson transformation method vs. those yielded by Rescale, Standardize, Normalize, and Box-Cox. These transformations seek to eliminate influence effects, and they are mainly syntactic modifications carried out on data without involving a change to the algorithm.
The pre-university variables pertaining to demographic and socio-demographic factors are not conclusive when trying to predict students’ academic performance, as their accuracy is around 65 %.
Although not always, the best result is provided by the same algorithm regarding per- semester academic performance. It can be stated that the KNN algorithm (accuracy greater than 77,5 %) provides good results, especially in even semesters, closely followed by Decision Trees (greater than 76,9 %) and the LDA method (greater than 76,5 %).
The results indicate that the prediction of academic performance using ML tools is a promising approach that can help improve students’ academic life and can allow institutions and teachers to take actions that contribute to the teaching-learning process.
Machine learning tools have been increasingly used in education in the last decade. This aspect, added to the detection of the variables that most influence academic performance, will allow to continue implementing other algorithms belonging to other branches within this field, such as assembly and deep learning methods.
In order to continue with the process of searching for models and algorithms that better predict academic performance, it is necessary to implement contemporary assembly methods (Bagging, Boosting, Voting), which belong to another branch of ML and are based on establishing different methods that work together in order to reduce errors.






















