I. INTRODUCCIÓN
La visualización en 3D por sistemas computacionales ha presentado grandes retos, ya que la adquisición de datos por medios convencionales (cámaras de visión estéreo) es en 2D [1]. El análisis en 3D por procesamiento de imágenes apareció primero con configuraciones y disposiciones adecuadas en pares de cámaras de visión estéreo [2], y posteriormente se han inventado elementos especializados para la medición en una dirección determinada (LIDAR) [3], o elementos multisensoriales integrados que brindan mayor información del entorno (Kinect) [4]. Existen otros elementos para esta función tales como los sensores tof (time of fligth) [5] y los sensores de relación de intensidad [6], entre otros; sin embargo, su efectividad no es alta (menor al 80 %), o sus métodos de procesamiento son complejos. Por otra parte, el LIDAR se usa en agricultura con el fin de revisar el estado de las plantaciones [7], y en el automovilismo inteligente para la detección de obstáculos [8]. El Kinect, además de usarse como interfaz para videojuegos [9], ha sido incorporado en el reconocimiento de posturas de la mano [10] y el control de altitud de un cuadricoptero [11].
En las medidas tridimensionales, la de mayor dificultad de integrar y procesar es la medida de profundidad [12]. Por tanto, se han realizado estudios con el fin de analizar adecuadamente esta magnitud e incorporar su aplicación [13] desde métodos clásicos [14], [15], últimas tecnologías [16] y unión de distintas técnicas [17]. Si bien los análisis arrojaron ciertos resultados que han ayudado a orientar este artículo, se encuentran ciertas carencias que se compensan de manera adecuada con conocimientos teóricos que se interrelacionan entre sí [18]. Al efectuar una medida se pueden utilizar uno o múltiples sensores que, con un adecuado análisis y elección (filtro) de los datos que provienen de estos, permitirán alcanzar una mayor confianza en la medición [19], [20].
Debido a que la visión 3d computacional es compleja (especialmente el eje de profundidad) a causa de error en los datos o redundancia excesiva en ellos, en el presente artículo se expondrá la incorporación de dos pares de sensores ópticos (visión estéreo-LIDAR y Kinect-LIDAR) para la medida de profundidad por medio de la fusión e integración sensorial, con procesamiento de los datos obtenidos por filtros de máxima verosimilitud [21] y de Kalman [22]. En este trabajo se evidencia cómo en los diferentes rangos de medidas de profundidad (0,68, 1,5, 2, 2,5 y 4 m) obtenidos con los dos sistemas de fusión sensorial -en particular la fusión Kinect-LIDAR e integración con filtro de Kalman-, sus errores absolutos son de menor valor en comparación con la medición por sensores individuales.
II. METODOLOGÍA Y MATERIALES
La interacción adecuada de los datos de diversos sensores que intervienen en una medición se debe diseñar de forma apropiada por medio de parámetros y técnicas que ayuden al control de los sensores y la información que ellos brindan [23]. Una de estas formas es la fusión e integración sensorial; la fusión se puede ver como la combinación de diferentes datos (de uno o varios sensores, en un mismo tiempo o instantes diferentes), y, por su parte, la integración es el uso de dicha información para la toma de decisión en un sistema de control [24], [25]. La idea básica de la fusión e integración multisensorial consiste en que la información obtenida por múltiples sensores puede llegar a ser más valiosa que la de un solo sensor, ya que los posibles errores en una medida se pueden compensar o reducir al efectuarla más de una vez [26].
En el análisis estadístico se necesitan planteamientos y algoritmos matemáticos (filtros) a fin de procesar y entender toda la información, de modo que en la integración sensorial se pueden aplicar dos técnicas: el filtro de máxima verosimilitud y el filtro de Kalman. Se trabaja con estos dos métodos ya que los filtros de media, mediana y moda solo ejecutan procesos de aproximación de primer orden, por lo que la influencia de datos erróneos, constantes o atípicos en el resultado es alta [27]. El primero se usa para ajustar un modelo y encontrar sus parámetros; es una extensión del proceso de decisión mediante el cual se calcula el valor de un parámetro al utilizar los valores de múltiples medidas relacionadas con dicho parámetro [27], [28]. Esta técnica enfocada en la fusión sensorial busca el valor de θ (entre todos los posibles) que haga más verosímil (más probable) el resultado que se ha obtenido. Para ello se calcula la función de probabilidad P (B;N|θ) y se elige el valor de θ que tenga mayor probabilidad [29]; de acuerdo con una distribución normal de los datos el planteamiento matemático de la función de verosimilitud θ = (μ, σ) [29] es:
El filtro de máxima verosimilitud trabaja con variables continuas, por lo que el análisis en sistemas computacionales utiliza aproximaciones de esta técnica [30]. Por otra parte, el filtro de Kalman es una herramienta matemática que se usa cuando se incluyen medidas del mundo real en el sistema lineal con el que se trabaja directamente [31]. El objetivo del filtro de Kalman es estimar los estados de una manera óptima, de forma que se minimice el índice del error cuadrático medio, por lo que representa una creencia o confianza en el estado xt en el tiempo t que viene dada por la media xt, y la covarianza pt. La entrada que recibe el filtro es la creencia en el tiempo t - 1, representada por xt -1 y pt-1. A fin de actualizar esta creencia también se necesitan las señales de control (ut) y las observaciones del entorno que proporcionan los sensores (zt). La salida del filtro de Kalman es la creencia en el instante de tiempo t, representada por xt y pt [31]-[33]. Por esta razón se busca un estimador óptimo del estado. Suponiendo que xˆk es la estimación en el instante k del estado, y zk+1 es el observador del estado xk en el instante k en el cual se le adiciona la incertidumbre del sensor y del sistema, el error se define como la diferencia entre el valor real del estado y la estimación (ecuación 2) [33].
El objetivo es minimizar el error en el n-ésimo estado. La matriz de covarianza del error es P (n) (ecuación 3) [32].
El algoritmo se ejecuta en dos pasos de forma iterativa [32]:
Predicción: antes de tener el valor Zk+1.
Corrección o actualización del estado, una vez conocido Zk+1.
En el presente artículo (conforme a investigaciones anteriores [13] y modificaciones pertinentes para este estudio [20]) se concibió una plataforma multisensorial que consta de dos partes: la primera, un componente hardware de fusión sensorial (HFS), y un segundo componente software de integración sensorial (SIS). Para el HFS se utilizaron como materiales: un radar láser Allen Bradley referencia Safe Zone Scanner Laser Multizone (LIDAR), cámaras Life Cam HD- 5.000, un Kinect, un cable serie RS232, una fuente de alimentación de 12 V/3 Amp, un conversor USB-Serie y un computador con procesador Intel core i5 de 2,3 ghz con memoria RAM de 4GB. Para la unión de los sensores se realizó un montaje constituido de cinco piezas: cuatro placas metálicas que permiten ajustar el escáner láser a una base superior en el eje vertical, la cual sostiene el sistema de visión. El HFS (Fig.1) presenta dos combinaciones de fusión sensorial: visión estéreo- LIDAR (Fig.1.a) y Kinect-LIDAR (Fig.1.b), ambos montajes tienen alineados sus centros de proyección.
En el SIS se implementan los filtros de máxima verosimilitud y Kalman. Estos algoritmos se programaron para el manejo de los datos obtenidos por el HFS en Open CV y lenguaje c++ con interfaz basada en qt. En este proceso se retoma una serie de algoritmos de trabajos previos [2], [13], [33], que se modificaron de acuerdo con las necesidades presentadas en la fusión sensorial. Por esta razón se realizó un diseño modular de acuerdo con las combinaciones: visión estéreo-LIDAR (Fig.2) y Kinect-LIDAR (Fig. 3).
A. Visión estéreo- LIDAR
El sistema de visión estéreo entrega una matriz de 320 x 240 datos, con información de las distancias a la que se encuentra un objeto en la escena, presente en la señal Reconstrucción 3d del entorno (Fig. 2). Esta se envía al módulo Procesamiento Visión Estéreo, el cual ejecuta un algoritmo encargado de calcular la señal Perfil de Distancias y δvisión, que denota el error del perfil de distancias de la visión estéreo. El sistema LIDAR entrega un vector de 720 datos con la información de la profundidad a la que se encuentra un objeto en la escena, denominado “Perfil de profundidades”, el cual se envía al módulo Procesamiento LIDAR que calcula la señal Perfil de Distancias y δláser, que denota el error del perfil de distancias del LIDAR. Las señales Perfil de Distancias Visión Estéreo y Perfil de Distancias Láser se compensan por las señales de error de los perfiles en el módulo de integración sensorial, de manera que se obtiene el vector de distancias de los datos fusionados en la señal Perfil de Datos Fusionado.
B. Kinect-LIDAR
El sistema Kinect brinda una imagen en escala de colores con información de las distancias a la que se encuentra un objeto en la escena, lo cual se procesa con un algoritmo a fin de obtener la señal Perfil de Distancias Kinect y δ Kinect (Fig. 3), que representa el error del perfil de distancias del Kinect. Los algoritmos empleados para la obtención de datos de profundidad se basaron en el software de código abierto RGBDemo [34].
III. RESULTADOS Y DISCUSIÓN
Escenarios de prueba
Se emplearon cuatro escenarios de prueba (Fig. 4) para las dos combinaciones del HFS. Los escenarios fueron usados para rangos de mediciones mayores y menores a un metro, el primero (Fig. 4.a) consta de dos cubos de cartón colocados en una mesa de 70 cm, el más grande con una cara perpendicular al eje de proyección óptica y el cubo menor tiene una leve inclinación respecto al otro. El segundo escenario (Fig. 4.b) consiste de tres cubos de cartón y un pequeño paralelepípedo todos sobre una mesa de 70 cm; cada objeto tiene una de sus caras perpendicular al eje de proyección óptico, y ambos escenarios se utilizaron en la combinación visión estéreo- LIDAR. En el tercer (Fig. 4.c) y cuarto (Figura 4.d) escenario se realizó la medición a 1 m de altura con diversos objetos, posicionando cada uno con una de sus caras perpendicular al eje de proyección de los sensores; estos últimos escenarios se usaron en la combinación Kinect-LIDAR.
Sistema visión estéreo-lidar
Con el fin de validar el sistema visión estéreo-LIDAR se realizaron tres pruebas en las que se colocaron obstáculos a distancias de 0,68, 1,5 y 2 m en el escenario de prueba 1 (Fig. 4.a). El límite se fijó en 2 m, ya que a partir de esta distancia el sistema no es operativo. Se indica con una línea horizontal en la Fig. 4.a la correlación visión estéreo (VE) y LIDAR. A los datos obtenidos en cada prueba se realiza integración sensorial con el filtro de máxima verosimilitud (MV) (figuras 5.a, 5.c y 5.e) y con el filtro de Kalman (figuras 5.b, 5.d y 5.f).
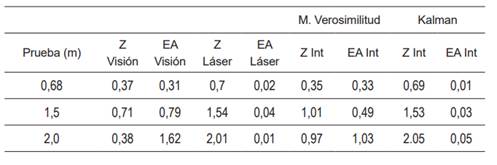
Los resultados con los filtros fueron ordenados (Tabla 1) con respecto a las distancias tomadas con visión estéreo (Z Visión), el LIDAR (Z Láser) y el resultado de la integración (Z Int), el error absoluto asociado a cada uno de ellos (EA visión, EA Láser y EA Int, respectivamente) y el promedio de estos.
Según la prueba 1 la integración sensorial con el filtro de máxima verosimilitud presenta un error de 33 cm, mientras que el filtro de Kalman presenta un error de 1 cm. En la prueba 2 con el filtro de máxima verosimilitud presenta un error de 49 cm, mientras que el filtro de Kalman presenta un error de 3cm. En la prueba 3 con el filtro de máxima verosimilitud presenta un error de 1,03 cm, mientras que el filtro de Kalman presenta un error de 5 cm.
Sistema Kinect-LIDAR
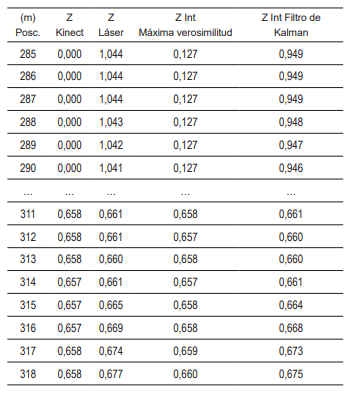
Con el fin de comprender la fusión e integración sensorial en el sistema Kinect-LIDAR se presentan 15 resultados promedio de 10 datos fusionados a una distancia aproximada de 0,67 m del sistema, con su respectivo equivalente tomado del Kinect y el LIDAR (véase la Tabla 2). En estos la integración con el filtro de Kalman corrige los valores erróneos de distancia 0 -desde las posiciones 284 hasta 290- del Kinect, a diferencia del filtro de máxima verosimilitud.
Para la validación del sistema Kinect-LIDAR se utilizaron los escenarios de prueba 2 (Fig. 4.b), 3 (Fig. 4.c) y 4 (Fig. 4.d), en los que se indica con una línea horizontal el perfil de línea que correlaciona el Kinect y LIDAR, para mediciones a 0,67, 2,5 y 4 m respectivamente. Se llevó a cabo la integración de los datos al realizar la interpolación de los datos nulos o incorrectos del Kinect por medio del filtro de máxima verosimilitud (Fig. 6.a, 6.c, 6.e), y el filtro de Kalman (Fig. 6.b, 6.d, 6.f).
Se presentan los resultados obtenidos (Tabla 3) al realizar la integración sensorial con el filtro de máxima verosimilitud y de Kalman. En estos se observan las distancias tomadas con el Kinect (Z Kinect), el láser (Z Láser), el resultado de fusionarlos (Z Int), el error absoluto asociado a cada uno de ellos (EA Kinect, EA Láser y EA Int respectivamente) y el promedio de estos.
Con respecto a la prueba 1 y 2, la integración sensorial con el filtro de máxima verosimilitud y el filtro de Kalman presenta un error de 1 cm. Por otra parte, la integración sensorial de la prueba 3 por máxima verosimilitud presenta un error de 10 cm, y el filtro de Kalman presenta un error de 1 cm.
De las dos fusiones de sensores se obtuvieron distintos resultados en conformidad con los escenarios de prueba. Esta información se procesó y filtró por las técnicas de máxima verosimilitud y de Kalman, lo que arrojó errores porcentuales para cada caso (Tabla 4).
IV. CONCLUSIONES
Se desarrollaron dos sistemas de fusión sensorial: visión estéreo-LIDAR, con un rango de medida comprendido entre 0,68 y 2,0 m, y un sistema de Kinect-LIDAR capaz de efectuar medidas entre 0,67 y 4,0 m; asimismo, dos herramientas software de integración sensorial por los filtros de máxima verosimilitud y Kalman.
La fusión sensorial de visión estéreo-LIDAR presenta un error porcentual general (EPG) de 23,28 % y, por otra parte, la unión Kinect-LIDAR arroja un EPG de 1,08 %. A su vez, el filtro de máxima verosimilitud tiene un EPG de 23,06 %, y el filtro de Kalman un EPG de 1,35 %. De esta manera, la fusión sensorial de mejor rendimiento es Kinect-LIDAR, y el procesamiento de mayor veracidad es el filtro de Kalman.
Los resultados obtenidos se deben a que el filtro de estimación de máxima verosimilitud se rige según las covarianzas dadas por los sensores, ya que el láser mide distancias lejanas y su covarianza es mayor que la del Kinect o las dos cámaras de visión estéreo, las cuales presentan datos en un rango más cercano. Por el contrario, el filtro de Kalman, a pesar de recibir información errada estima y corrige el valor de la medida, de manera que es una técnica robusta para la fusión e integración de datos.