1. INTRODUCCIÓN

En términos generales, puede afirmarse que cualquier obra construida por el hombre está soportada por el suelo o roca de la corteza terrestre [¹]. El estudio del comportamiento geotécnico de los suelos se ha desarrollado en consideración a que los suelos se encuentran saturados o secos [²]. Los suelos parcialmente saturados se encuentran sobre el nivel freático y pueden llegar incluso a estar secos en zonas cercanas a la superficie, tal como se muestra en la figura 1.

FIGURA 1 ZONAS DE SUELO SATURADO Y PARCIALMENTE SATURADO [³] 

La succión es la capacidad que tiene un suelo de retener el agua en sus poros, lo que origina una fuerza interna. Esta es una de las principales variables en el estudio de los suelos parcialmente saturados y resulta una variable fundamental para la comprensión de diferentes fenómenos. La determinación de la curva característica del suelo es la base del comportamiento ingenieril de los suelos parcialmente saturados, la cual define la capacidad del suelo para rechazar o almacenar agua a partir de relacionar la cantidad de agua retenida por el suelo con la succión correspondiente. Adicionalmente, la curva característica no es única para un suelo; su forma y posición varían para las trayectorias de humedecimiento y secado, fenómeno denominado "histéresis". Los principales problemas de tipo geotécnico abarcan la inestabilidad de taludes, alta sensibilidad, agrietamiento y dificultades tales como humedad excesiva y consistencia muy blanda al usarse como materiales de construcción [⁴].

2. ANÁLISIS DE ESTABILIDAD EN TALUDES DE PRESAS DE TIERRA

Las presas de tierra son obras de ingeniería construidas para almacenar y distribuir las reservas de agua con el objetivo de obtener beneficios económicos y sociales. Esto con el fin de establecer un equilibrio entre los usos del agua y las necesidades de los ecosistemas vitales, al promover el desarrollo sostenible, la democracia, la participación, la equidad y el respeto por los derechos de las poblaciones más vulnerables [⁵].

Se contabilizaron los fallos en presas de tierra en Cuba luego de realizar visitas a las empresas de aprovechamiento hidráulico de todas las provincias del país [⁶]. Con base en estos estudios, el orden actual de ocurrencia de las causas más comunes de falla en presas de tierra en Cuba difieren ligeramente con respecto al resto del mundo y son: el deslizamiento de los taludes, el rebase de la cortina, el sifonamiento, las pérdidas por filtraciones y el agrietamiento.

Los deslizamientos de taludes se producen debido a que el peso de la masa de suelo es mayor que su propia resistencia a cortante en una superficie de corte y suelen considerarse divididas en tres tipos principales: las fallas al final de la construcción, las fallas durante la operación y las fallas luego de un desembalse rápido. Todas las fallas de importancia reportadas por deslizamientos del talud aguas arriba han ocurrido como consecuencia de un desembalse rápido y, aunque no han causado el colapso de la presa o la pérdida de agua en el almacenamiento, sí provocan situaciones de peligro al tapar conductos y galerías.

En el análisis de la estabilidad de taludes el método de las dovelas puede considerarse preciso a partir de la aplicación de las teorías de Morgenstern-Price, si se asume que existe una función que relaciona las fuerzas de cortante y las fuerzas normales entre dovelas. Se establece una relación entre los componentes de las fuerzas de interconexión, tal como se muestra en la ecuación 1.

Donde X, E son las fuerzas de interconexión relacionadas entre sí y A es el factor de escala.

La función f (x) se selecciona de forma arbitraria y su influencia es poco sustancial. La particularidad del método es que la masa se subdivide en franjas infinitésimas, a las cuales se imponen las ecuaciones de equilibrio en la traslación horizontal, vertical y de rotura en la base de las franjas. A partir de este punto se obtiene la ecuación de fuerzas:

Donde FS es el factor de seguridad, dWes el peso de la franja infinitésima, dUson las presiones neutras en la base, c' es la cohesión efectiva, φ’ es el ángulo de fricción interna efectivo y a es la inclinación de la base de la dovela respecto a la horizontal.

Se escribe otra ecuación de equilibrio, en este caso, de momento, al proponer una restricción de la rotación con respecto a la base:

Este método satisface todas las ecuaciones de equilibrio y puede aplicarse a cualquier superficie de deslizamiento. Si bien se puede considerar cualquier forma de función en el análisis, una función irreal puede resultar en problemas de convergencia en la solución de las ecuaciones para el factor de seguridad. En la práctica de la ingeniería es común definir la estabilidad de un talud en términos de un factor de seguridad (FS), obtenido habitualmente de un análisis matemático determinístico cuyas formulaciones deben tener en cuenta la mayoría de los factores que afectan la estabilidad.

La envolvente de falla extendida de Mohr-Coulomb para los suelos parcialmente saturados toma la forma matemática que se muestra en la ecuación 4 [⁷], [⁸].

Donde σ es la tensión normal en la falla, (u_a - u_w ) es la succión, c' es la cohesión efectiva, d)'es el ángulo de fricción interna efectivo, y Ф^b es el ángulo de succión del suelo.

La ecuación de resistencia al corte para suelos no saturados muestra la transición hacia la condición saturada. Si el suelo está próximo a su saturación de agua, la presión de poro de agua (u_w) tiende a igualar la presión de poro de aire (u_a), en tanto la succión mátrica tiende a cero [⁹].

A partir de lo planteado por Armas [¹⁰], [¹¹] se presenta la tabla 1, en la que se resumen los valores de factor de seguridad en función de las condiciones de trabajo y de la categoría de la presa.

TABLA 1 ENTORNO DE LOS VALORES DE FACTOR DE SEGURIDAD DE ACUERDO A LA CATEGORÍA DE LA OBRA [¹⁰] 

Fuente: Armas y Horta, 1987.

El paquete de programas recogidos dentro del GeoStudio 2012 se basa en los diversos análisis que comprenden el suelo como componente fundamental, utilizado para el diseño y la revisión de cimentaciones y presas de tierra, en la determinación de la red de flujo, la estabilidad de taludes y terraplenes, entre otros. Presenta la posibilidad de calcular el factor de seguridad en presas de tierra a partir de la implementación de diversos métodos matemáticos. En esta investigación se utilizan dos de sus componentes: SEEP/W y SLOPE/W. A fin de obtener el factor de seguridad en la estabilidad de taludes, el SLOPE/W tiene implementada la ecuación 5.

Donde σ_n es la tensión normal en el centro de la base de una dovela y FS es el factor de seguridad definido como el factor para el cual los parámetros de resistencia al corte deben reducirse a fin de llevar la masa de suelo a un estado de equilibrio límite a lo largo de la superficie de deslizamiento supuesta. Los restantes parámetros se obtienen a partir de la aplicación de la envolvente de falla extendida de Morh-Coulomb.

SLOPE/W solo considera las condiciones de resistencia al corte no saturadas cuando las presiones de poros son negativas. En estas condiciones, el ángulo de succión (Φ^b) se utiliza para calcular la fuerza de fuerza de corte movilizada en la base de cada dovela. Cuando el ángulo de succión (Φ^b) se deja en blanco o se establece en 0° no habrá un aumento en la resistencia al corte debido a la succión. Cuando el ángulo de succión (Φ^b) se iguala al ángulo de fricción interna efectivo (qV) se indica que las presiones de poros negativas serán tan efectivas para aumentar la resistencia al corte del suelo como las presiones de poros positivas para reducirla. Por lo general, el ángulo de succión (Φ^b) es mayor que cero, pero menor que el ángulo de fricción interna efectivo (Φ). El inconveniente del uso del ángulo de succión (Φ^b) como una constante es que se supone que la envolvente de falla extendida de Mohr-Coulomb aumenta linealmente con la succión del suelo, lo que tiende a sobrestimar la resistencia al corte del suelo parcialmente saturado, particularmente cuando la succión del suelo es muy alta. Como mejor alternativa al uso del ángulo de succión (Φ^b) SLOPE/W implementó la ecuación 6 propuesta por [¹²].

Donde, θ_w es el contenido volumétrico de agua, θ_s es el contenido volumétrico saturado de agua y θ_r es el contenido volumétrico residual de agua. En el SLOPE/W se supone que el contenido volumétrico residual de agua es igual al 10 % del contenido volumétrico saturado de agua, por lo que el ángulo de succión (Φ^b) no se utiliza en la ecuación anterior, sino que la resistencia al corte del suelo parcialmente saturado se estima en función de la curva característica y de los parámetros de resistencia al corte saturado del suelo. La teoría fundamental planteada en el programa es la mencionada por [⁸].

3. METODOLOGÍA

A partir de estudios realizados por el Instituto Nacional de Recursos Hidráulicos (INRH) se conoce que en Cuba existen doscientas cuarenta y un presas, de las cuales el 62 % presenta altura de cortina inferior a veintidós metros y cuyos procesos de construcción y mantenimiento se realizan en consideración a la mecánica de suelos tradicional. En esta investigación se analiza la estabilidad del talud aguas arriba en una presa de tierra homogénea, sin berma y con prisma de drenaje, sometida a un proceso de sequía durante noventa días y bajo las leyes de la mecánica de suelos saturados y parcialmente saturados. El modelo correspondiente se muestra en la figura 2.

Fuente: elaboración propia.

FIGURA 2 GEOMETRÍA DEL MODELO 

En el propósito de definir los materiales que conformarán la cortina de la presa se consideraron tres suelos con clasificación CH (arcilla de alta compresibilidad), cada uno de los cuales presenta una curva característica obtenidas para el 95 % del grado de compactación [⁷], [¹³], las cuales se muestran en las figuras 3, 4 y 5. La relación de permeabilidad establecida es de kx = 12ky, a fin de respetar el comportamiento de los suelos compactados. Las características de los tres suelos utilizados para la cortina se muestran en la tabla 2.

TABLA 2 CARACTERÍSTICAS DE LOS SUELOS 

Fuente: Tristá, 2015; Rodríguez, 2017.

Fuente: Rodríguez, 2017.

FIGURA 3 CURVA CARACTERÍSTICA DEL SUELO A 

Fuente: Tristá, 2015.

FIGURA 4 CURVA CARACTERÍSTICA DEL SUELO B 

Fuente: Tristá, 2015.

FIGURA 5 CURVA CARACTERÍSTICA DEL SUELO C 

Para aplicar en el análisis las consideraciones de los suelos parcialmente saturados se tiene en cuenta la teoría planteada en la sección 2 de este artículo, en la cual se define la obtención del FS parcialmente saturado a partir de los parámetros de resistencia al corte obtenidos en estado saturado y la incorporación de la curva característica obtenida en el laboratorio, lo que posibilita la aplicación de la ecuación 6 y, por ende, la modificación del FS sin variar los parámetros de resistencia al corte iniciales (cohesión y ángulo de fricción interna efectivos saturados).

Los suelos para la cimentación y el drenaje se muestran la tabla 3. En la cimentación se considera una arena arcillosa y en el drenaje se considera una grava de alta permeabilidad, según lo planteado por [¹⁴], [¹⁵].

TABLA 3 CARACTERÍSTICAS DE LOS SUELOS DE LA CIMENTACIÓN Y EL DRENAJE 

Fuente: elaboración propia.

En los análisis de flujo transitorio, a diferencia del flujo establecido, se presentan cargas hidráulicas variables con respecto al tiempo. La ecuación de Richards, propuesta en 1931, describe este proceso, a partir del cual, con condiciones de frontera y condiciones iniciales apropiadas, proporciona los campos de succión en el espacio y el tiempo, tal como se muestra en la ecuación 7.

Donde h_m es la carga de succión, k_y(h_m) es la función de conductividad hidráulica, ∂/∂_z es el término adicional en la dirección del eje z debido a la presencia de la carga de elevación, Ces la capacidad específica de humedad, y ∂θ /∂t es la pendiente de la relación entre el contenido de agua volumétrico y el tiempo. Por tanto, para hacer uso de esta ecuación se requiere la definición de la curva característica y la función de conductividad hidráulica del suelo [⁹] grados de saturaci\u00f3n, velocidades de flujo, fuerzas de filtraci\u00f3n, cargas hidr\u00eiulicas y presiones de poro.

A fin de considerar el efecto del desembalse rápido de la presa, a partir del flujo transitorio, producto de un periodo de sequía prolongada, se supone que el nivel de las aguas descenderán a razón de 15cm/ día. Si la presa tiene inicialmente el nivel de aguas normales (NAN) con una altura de diecisiete metros, para reducir su nivel hasta el de aguas muertas (NAM) a 4,4 metros, se necesitarán cerca de noventa días. En la figura 6 se muestra la variación en los niveles de agua considerados.

Fuente: elaboración propia.

FIGURA 6 NIVELES DE AGUA ESTABLECIDOS AL INICIO Y AL FINAL DEL DESEMBALSE RÁPIDO 

4. RESULTADOS Y DISCUSIÓN

Una vez realizada la modelación, se obtienen los diferentes niveles de agua durante los noventa días de duración del desembalse a partir de considerar el proceso de filtración transitoria en el SEEP/W; adicionalmente, se muestra la modificación de la superficie de falla (estas etapas se muestran en la figura 7 y 8).

Fuente: elaboración propia.

FIGURA 7 NIVELES DE AGUA EN LAS DIFERENTES ETAPAS DEL DESEMBALSE RÁPIDO 

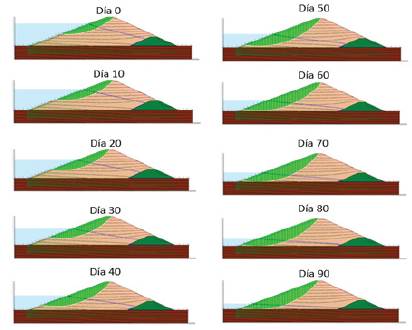
Fuente: elaboración propia.

FIGURA 8 SUPERFICIE DE FALLA EN LAS DIFERENTES ETAPAS DEL DESEMBALSE RÁPIDO 

Una vez obtenido el comportamiento de la red de flujo y de la superficie de falla durante el desembalse rápido se analiza la variación del factor de seguridad en el talud aguas arriba durante este proceso. Los resultados se muestran en las figuras 9, 10 y 11.

Fuente: elaboración propia.

FIGURA 9 COMPORTAMIENTO DEL FACTOR DE SEGURIDAD PARA LOS SUELOS ESTUDIADOS EN ESTADO SATURADO 

Fuente: Elaboración propia.

FIGURA 10 COMPORTAMIENTO DEL FACTOR DE SEGURIDAD PARA LOS SUELOS ESTUDIADOS EN ESTADO PARCIALMENTE SATURADO, RAMA EN HUMEDECIMIENTO 

Fuente: elaboración propia.

FIGURA 11 COMPORTAMIENTO DEL FACTOR DE SEGURIDAD PARA LOS SUELOS ESTUDIADOS EN ESTADO PARCIALMENTE SATURADO, RAMA EN SECADO 

En las figuras anteriores pudo apreciarse que el factor de seguridad disminuye de manera progresiva a medida que pasan los días y se reduce el nivel de agua en la presa. Adicionalmente, el suelo B es el que presenta los mayores factores de seguridad iniciales, mientras que el suelo C presenta los menores valores; aunque es este último el que apenas sufre modificaciones durante el proceso de desembalse rápido; por el contrario, los suelos A y B sufren una abrupta reducción en el factor de seguridad. Los resultados de los factores de seguridad obtenidos y la variación porcentual entre ellos al inicio, en el día 0 y al final del proceso de desembalse, en el día 90, se muestran en la tabla 4 y la figura 12.

TABLA 4 FS Y VARIACIÓN PORCENTUAL ENTRE EL DÍA 0 Y EL DÍA 90 

Fuente: elaboración propia.

Fuente: elaboración propia.

FIGURA 12 INCREMENTO PORCENTUAL DEL FACTOR DE SEGURIDAD PARA TODOS LOS CASOS ANALIZADOS 

Puede observarse que para todos los casos el incremento es superior al 5 %, lo cual representa que el valor es significativo desde el punto de vista ingenieril. Para la rama en secado el incremento es inferior al obtenido en estado saturado y con la rama en humedecimiento en los tres suelos considerados en la investigación.

Luego, se muestra el comportamiento de cada suelo por separado en las figuras 13, 14 y 15.

Fuente: elaboración propia.

FIGURA 13 DESEMBALSE RÁPIDO CON EL SUELO A EN ESTADO SATURADO Y PARCIALMENTE SATURADO 

Fuente: elaboración propia.

FIGURA 14 DESEMBALSE RÁPIDO CON EL SUELO B EN ESTADO SATURADO Y PARCIALMENTE SATURADO 

Fuente: elaboración propia.

FIGURA 15 DESEMBALSE RÁPIDO CON EL SUELO C EN ESTADO SATURADO Y PARCIALMENTE SATURADO 

En las figuras 13, 14 y 15 puede apreciarse que, si bien los tres suelos tienen la misma clasificación por el Sistema Unificado de Clasificación de Suelos (SUCS), presentan comportamientos diversos ante el fenómeno analizado. El suelo A presenta variaciones del orden del 2 % entre el estado saturado y el parcialmente saturado, esto al considerar ambas curvas, ya que el comportamiento en secado y en humedecimiento prácticamente no varía. El suelo B muestra variaciones en humedecimiento entre el 3 % y el 13 % al inicio y al final del desembalse rápido; en secado las variaciones oscilan entre el 3 % y el 8 %. Estos valores se obtienen respecto al suelo en estado saturado. En el suelo C las variaciones se incrementan, y oscilan entre el 18 % y el 23 % en humedecimiento, y entre el 26 % y el 31 % en secado respecto al suelo en estado saturado. En ninguno de los casos se evidencian factores de seguridad inferiores a 1, por lo que, para la geometría planteada y los suelos considerados, el talud aguas arriba mantiene aún las condiciones de seguridad y estabilidad establecidas inicialmente.

5. CONCLUSIONES

A partir de lo expuesto es posible concluir que durante un periodo de sequía prolongada el nivel de agua de las presas de tierra se reduce de manera significativa, lo que provoca, a su vez, una disminución del factor de seguridad en el talud aguas arriba. Esta pérdida de estabilidad puede asociarse o no a fenómenos de colapso de estas estructuras, lo que provocaría otras consecuencias indeseables que podrían derivar en la pérdida de vidas humanas y de recursos materiales.

Si se consideran en el análisis las leyes de la mecánica de suelos parcialmente saturados, existe un incremento significativo del factor de seguridad cuando se desarrolla el fenómeno de desembalse rápido producto a la sequía prolongada. Esta consideración posibilita obtener factores de seguridad que responden con mayor precisión al fenómeno que se genera en el interior del talud, dado que la curva característica del suelo describe su comportamiento durante fenómenos de pérdida de humedad.

En el caso del desembalse rápido, dado que el proceso que ocurre es el de secado, la rama de la curva característica que se recomienda incluir en el estudio del mismo es la de secado, a fin de mostrar consecuencia con el proceso estudiado.

Aunque los tres suelos considerados en la investigación clasifican como arcilla de alta compresibilidad, el comportamiento individual difiere. Esto está referido a los parámetros físico-mecánicos obtenidos en cada caso. Por tanto, la estabilidad se asocia directamente a la cohesión, al ángulo de fricción interna y al peso específico del suelo en cuestión. Con la geometría planteada no se observan valores de factor de seguridad inferiores a 1,1 en ninguno de los casos analizados, por lo que puede considerarse que la presa mantiene sus condiciones de seguridad y estabilidad, aunque esto no significa que el comportamiento sea el mismo para presas con geometrías diferentes.