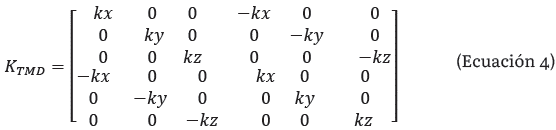INTRODUCCIÓN
Las estructuras son cada vez más esbeltas, lo cual las hace susceptibles de vibraciones debido al paso peatonal y vientos, condiciones que podrían alterar el funcionamiento y el confort de ocupación. Una manera de atenuar las vibraciones excesivas es el uso de dispositivos de control, mecanismos diseñados para apaciguar las cargas dinámicas [1], [2], que consisten en un sistema de un solo grado de libertad, compuesto por una masa, un resorte y un amortiguador. Este se sintoniza en resonancia con la estructura primaria, lo que permite que una gran cantidad de energía de vibración se transfiera al dispositivo y luego se disipe por amortiguación en el TMD cuando la estructura primaria se somete a excitaciones armónicas [3], [4].
El principal objetivo de este artículo es el estudio de una viga simplemente apoyada, equipada con un sistema de control de vibraciones "TMD", el cual será evaluado y diseñado utilizando las funciones de respuesta en frecuencia de la viga con y sin AMS [3]. Con el propósito de verificar el efecto de las propiedades dinámicas del AMS, se determinaron las frecuencias naturales, modos de vibración y relación de amortiguamiento [5].
En cuanto al diseño de los amortiguadores de masa sintonizada, se han realizado investigaciones en las que se muestra la importancia de algunas características para su construcción. Chen et al. [5] exponen que las frecuencias naturales y las formas de modo de una viga Timoshenko son información de importancia básica para el diseño de TMD, con el fin de controlar la vibración de una viga. Si un TMD simple o múltiple debe diseñarse para controlar la vibración de la viga, debe depender de la forma del modo de la viga que se desea controlar. Por supuesto, la posición de la fuerza o momento de excitación armónica y el punto de control en la viga también deben tenerse en cuenta. Chi Tho et al. [6] llevaron a cabo modelos numéricos de elementos finitos comparando con otros autores y presentando resultados dinámicos, en cuanto a problemas de vibración dinámica y sistemas de trama espacial con TMD, combinando modelos de inteligencia artificial. Además, se presentaron resultados de los problemas de reducción de las vibraciones con los TMD bajo una carga aleatoria, descritos como un proceso estacionario con ruido blanco [7].
Asimismo, teniendo en cuenta los principales inconvenientes de los dispositivos convencionales, los cuales son el derrame de aceite o gas que afectan la rigidez y disminuyen la vida útil del mecanismo [8], se propone la incorporación de un amortiguador magnético partiendo de la investigación realizada por Babak et al. [9], quienes realizaron la configuración de imán permanente en el diseño de un amortiguador de corrientes de Foucault, elementos en suspensión que atenúan tanto las vibraciones como los efectos de carga de choque.
Este artículo está dividido en cuatro secciones principales. La primera presenta el estado del arte; la segunda 2 muestra la formulación de la validación con un software, y la incorporación del amortiguador de forma numérica. En la tercera se realiza la comparación en los modos de vibración con y sin el amortiguador, la verificación de resultados y las discusiones. En la cuarta se presenta el análisis de resultados y conclusiones.
MODELO FÍSICO Y NUMÉRICO
Descripción de la viga
Como ya se mencionó, en esta sección se presenta el modelo físico y numérico para el diseño óptimo del amortiguador de masa sintonizada. Para ello se eligieron las propiedades de una estructura que fue usada como objeto de estudio [3], [10], una viga de acero simplemente apoyada con las siguientes propiedades físicas y mecánicas: longitud: 1,467m; altura: 0,00794m; ancho: 0,076m; densidad: 7.850  , módulo de elasticidad:
, módulo de elasticidad: 
Método numérico de elementos finitos
Para el análisis de la viga, usando el método de elementos finitos, se comprueba que al aplicar 10 elementos el error en los resultados se reduce si se comparan las frecuencias usando una menor cantidad de elementos, como se muestra en la gráfica 1. Del mismo modo, a medida que el número de frecuencias aumentan es necesario aplicar más nodos para que los resultados sean los más acertados posibles.
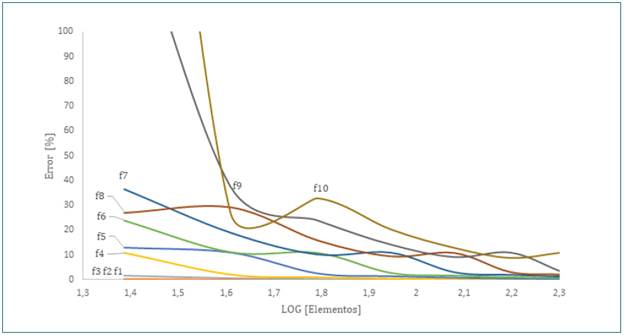
GRÁFICA 1 VARIACIÓN DE FRECUENCIAS OBTENIDAS POR FÓRMULA ANALÍTICA Y MODELO NUMÉRICO EN MATLAB SEGÚN LA CANTIDAD DE ELEMENTOS
Cada nodo cuenta con tres grados de libertad: desplazamientos horizontales [PJ, desplazamientos verticales [Pv] y un momento [M] como se refleja en la ilustración 2. Estos grados de libertad se reducen, ya que hay nodos donde no existen fuerzas actuantes que permitan deformaciones o desplazamientos. Con la cantidad de grados de libertad calculados se realizaron tres matrices que permiten el análisis dinámico del elemento: masa, rigidez y rotación de coordenadas.
Las matrices calculadas de masa y de rigidez permitirán obtener las frecuencias naturales del elemento a partir de la siguiente fórmula:
Una vez obtenidos los resultados para la viga, se procede a incorporar el amortiguador de masa sintonizada. Para ello, se debe tener en cuenta la matriz de rigidez, la cual será aplicada en el nodo que le corresponda del arreglo global, según su ubicación en el elemento.
La masa del resorte será posicionada en el nodo que se encuentra conectado con el amortiguador, aplicándola en la componente vertical de dicha sección [11].
Amortiguamiento
El amortiguamiento es proporcional a la masa y la rigidez de la viga, lo que permite incorporar y modelar una disipación de la energía proveniente de las deformaciones que pueda sufrir el elemento.
Usando la teoría de amortiguamiento de Rayleigh [11], se analizan fragmentos de modelación para cada nodo, extrayendo fracciones de amortiguamiento "ζ" que producirán una variación en las frecuencias naturales. El diseño garantiza que los valores de amortiguamiento reduzcan las frecuencias al ser incorporado a la viga.
Los coeficientes α 0 y α1 se determinan a partir de fracciones de amortiguamiento, las cuales son calculadas con las siguientes expresiones:
Parámetros óptimos del amortiguado de masa sintonizada (AMS)
Determinación de parámetros óptimos para el amortiguador de masa sintonizada
Para determinar los parámetros óptimos del amortiguador de masa sintonizada, se utilizaron las ecuaciones propuestas por Den Hartog [12] para el análisis de sistemas con un grado de libertad.
De acuerdo con esta publicación [13], la relación de masas se define con la siguiente ecuación:
Además, la relación entre la frecuencia natural obtenida con el TMD y la frecuencia natural de la viga, comúnmente denominada la razón entre frecuencias optima, se define como
La razón de amortiguamiento óptimo se encuentra relacionada por
Con las expresiones mencionadas se pueden calcular los parámetros óptimos para un TMD, de tal manera que dicho dispositivo sintonice armónicamente con la viga y el diseño sea eficiente. Con los valores obtenidos en las relaciones es posible determinar el coeficiente de amortiguamiento óptimo con la siguiente expresión [11]:
De acuerdo con Chen et al. [5], y los resultados obtenidos por Ávila et al. [14] con el fin de que el amortiguador tenga una funcionalidad adecuada, la relación de las masas debe encontrarse entre el 1 y el 15 %. El valor usado en esta investigación fue del 5 %, el cual fue seleccionado por su efecto en el elemento de estudio.
PROPUESTA DE DISEÑO Y EVALUACIÓN DEL AMS
Diseño del amortiguador magnético
Cuando un campo magnético variable atraviesa un conductor eléctrico, debido al fenómeno de la inducción magnética, crea corrientes que al circular por un conductor producen un campo magnético que se opone al medio. Entre más denso sea el campo magnético, las corrientes serán más fuertes, que también son directamente proporcionales a la velocidad relativa de movimiento [15]. Dichas corrientes invisibles producen una alteración en el medio que causa circulación de electrones y, por consiguiente, una alteración en la interacción del campo magnético con los componentes físicos por medio de fuerzas repulsivas y/o de atracción [16].
Para diseñar el amortiguador fueron considerados los resultados obtenidos por Babak, Mir y Golnaraghi [9], una variación del diseño base. Con los datos teóricos y experimentales propuestos en su investigación se ingresan valores propios como lo es el coeficiente de amortiguamiento, para modificar parámetros como distancia entre imanes, fuerza magnética, posición del disco de aluminio, entre otros [9], [17]. Tal y como se muestra en la siguiente gráfica:
Resultados obtenidos para el análisis de vibración sin TMD
Las frecuencias naturales obtenidas en este trabajo se calcularon utilizando las matrices de masa, rigidez y amortiguamiento obtenidas con el método de elementos finitos formuladas en Matlab [18]. Con el fin de validar esta metodología, los resultados fueron comparados con las frecuencias de la viga con y sin el AMS por medio del modelo diseñado en el software Midas Gen 2019 [19].
Para el análisis de la viga se varía la cantidad de elementos, con el fin de encontrar un valor óptimo, que permita asemejar las frecuencias con las calculadas, usando la fórmula analítica.
De acuerdo con la gráfica 1, la viga es fraccionada en 10 elementos, ya que los resultados que se obtienen son los menos alejados a los obtenidos analíticamente:
TABLA 1 COMPARACIÓN DE FRECUENCIAS OBTENIDAS CON EL SOFTWARE MIDAS GEN Y EL MODELO NUMÉRICO DE MATLAB
| frecuencias | Matlab [Hz] | Midas Gen [Hz] | Error[%] |
|---|---|---|---|
| f1 | 8,643 | 8,653 | 0,113 |
| f2 | 34,576 | 34,612 | 0,104 |
| f3 | 77,828 | 77,899 | 0,091 |
| f4 | 138,516 | 138,617 | 0,073 |
| f5 | 216,927 | 217,038 | 0,051 |
| f6 | 313,617 | 313,702 | 0,027 |
| f7 | 429,509 | 429,509 | 0,000 |
| f8 | 565,892 | 565,717 | 0,031 |
| f9 | 723,761 | 723,223 | 0,074 |
| f10 | 959,297 | 960,407 | 0,116 |
Modos de vibración
Los vectores propios son usados para definir los modos de vibración de la estructura. Estos son directamente proporcionales a la cantidad de grados de libertad que posee el elemento. A continuación, se ilustran los primeros modos de vibración de la viga simplemente apoyada:
Parámetros óptimos del amortiguador
La tabla 2 presenta los valores óptimos de la configuración para una viga con un TMD.
Características y dimensiones del amortiguador magnético
De acuerdo con la configuración propuesta [9], los parámetros usados como base para el diseño del amortiguador son:
TABLA 3 PROPIEDADES DEL AMORTIGUADOR MAGNÉTICO PROPUESTO [8]
| Propiedades | Valor |
|---|---|
| Conductividad eléctrica de aluminio | 3,37e7 (S/m) |
| Diámetro interno de la placa de aluminio | 38 (mm) |
| Diámetro externo de la placa de aluminio | 100 (mm) |
| Grosor de la placa de aluminio | 8 (mm) |
| Diámetro del imán permanente | 25 (mm) |
| Longitud del imán permanente | 20 (mm) |
| Magnetización del imán permanente | 1,03e6 (A/m) |
| Composición permanente del imán | NdFeB42 |
En consecuencia, con el amortiguamiento obtenido se adapta el modelo usando los resultados teóricos y experimentales [9].
TABLA 4 PROPIEDADES AJUSTADAS A LA VIGA DE ESTUDIO PARA EL DISEÑO DEL AMORTIGUADOR
| Propiedades | Valor | |
|---|---|---|
| Coeficiente de amortiguamiento | 14,937 | (Ns/m) |
| Radio exterior disco Al | 0,026 | (m) |
| Altura disco | 0,014 | (m) |
| Distancia entre imanes | 0,025 | (m) |
| Relación amortiguamiento | 11,6 | (Ns/m) |
| Fuerza Magnética | 14 | (N) |
| Densidad Flujo magnético | 0,04 | (T) |
Resultados obtenidos para el análisis de vibración con TMD
Considerando las especificaciones del modelo anterior, se ubica un amortiguador de masa sintonizada en el centro de la luz considerando las siguientes propiedades [20]:
Al igual que en el modelo de la sección Resultados obtenidos para el análisis de vibración sin TMD, la viga se discretiza en 10 elementos, y se calculan las frecuencias de la viga incorporando el TMD, tanto en el código realizado en Matlab como en el modelo hecho en el software Midas Gen:
TABLA 5 FRECUENCIAS OBTENIDAS INCORPORANDO EL AMORTIGUADOR A LA VIGA
| Masa (%) | C. amort. C (Ns/m) | Rigidez K (N/m) | Viga con TMD | |||
|---|---|---|---|---|---|---|
| Frecuencias (Hz) | Midas Gen | Matlab | % error | |||
| 5 | 14,934 | 451,26 | f | 5,536 | 5,875 | 6,13 |
| f | 8,968 | 8,578 | 4,34 | |||
| f3 | 34,612 | 33,782 | 2,40 | |||
| f4 | 77,92 | 76,029 | 2,43 | |||
| f5 | 138,62 | 135,336 | 2,37 | |||
| f6 | 217,05 | 211,940 | 2,35 | |||
| ff | 313,70 | 306,416 | 2,32 | |||
| f8 | 429,51 | 419,643 | 2,30 | |||
| f9 | 565,72 | 552,897 | 2,27 | |||
| F10 | 723,23 | 707,138 | 2,22 | |||
Función de respuesta en frecuencia
Con el propósito de verificar el desempeño de la propuesta de diseño del dispositivo en el control de las vibraciones, se utilizó la función respuesta en frecuencia (FRF), relacionando una respuesta de impacto y de salida.
Se obtuvieron FRF para tres casos: resultados sin amortiguador, luego incorporando 1 y 2 TMD.
Respecto a los resultados obtenidos con un único amortiguador, se comprueba la efectividad en la implementación de parámetros óptimos para este elemento, ya que se obtuvieron reducciones importantes en la amplitud de la respuesta en frecuencia. El amortiguador se ubicó en L/2 de la viga de estudio, la fuerza fue aplicada a 0,20 m y el sensor para captura de resultados a 1,20 m de la viga, consiguiendo reducciones del 91,78, 46,32 % y 5,32 % respecto a las amplitudes obtenidas sin TMD.
En el análisis de la respuesta en frecuencia se encontró que resulta más efectivo para la reducción de las amplitudes en las primeras frecuencias la implementación de dos amortiguadores de masa sintonizada. Los amortiguadores se ubicaron a L/4 y 3L/4, y se obtuvieron reducciones en los valores de amplitud de respuesta en frecuencia de 95,68, 98,57, 99,56 % frente a los obtenidos sin la implementación de los dispositivos de control.
Es recomendable utilizar diferentes parámetros para el TMD de rigidez, para que las frecuencias difieran y la gráfica no sufra traslapos de magnitud. Usando ecuaciones de movimiento para un grado de libertad, se calcula un nuevo K aplicado al segundo amortiguador. Dicha rigidez no difiere significativamente del primer TMD de 520 N/m.
CONCLUSIONES
Este artículo presenta el diseño de un AMS para una viga que puede ser utilizada en modelos dinámicos de laboratorio. En el diseño se consideró un amortiguador que utiliza como principio las corrientes de Foucault. Para verificar el desempeño del AMS se obtuvieron las funciones de respuesta en frecuencia.
Considerando este contexto, las principales conclusiones obtenidas en este estudio son:
Se comprueba la viabilidad del AMS aplicado en la viga simplemente apoyada, evidenciando una reducción importante en las frecuencias al incorporar el AMS en el centro de la luz. Así mismo, es más efectivo incorporar un segundo AMS con características similares; permite un mejor desempeño en la respuesta dinámica de la viga.
Es factible la construcción del AMS, ya que los parámetros de diseño para el amortiguador magnético se encuentran de acuerdo con la caracterización de las investigaciones realizadas por Babak, Mir y Golnaraghi, las cuales permiten asumir parámetros propios y acoplar el mecanismo a esta investigación.
El número de elementos utilizados para la discretización de la viga es proporcional a la certeza de los resultados: entre más elementos sean aplicados a la estructura de estudio, mayor será la convergencia a la respuesta obtenida por medio de una fórmula analítica. Esto comprueba que son necesarios más de 6 elementos para obtener errores mínimos.
En consecuencia, con los resultados obtenidos en este trabajo se sugiere a futuros autores llevar a cabo el modelo propuesto de manera experimental, a fin de corroborar que la optimización realizada sea la adecuada para la disminución de la respuesta en frecuencia.