Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.1 no.4 Bucaramanga Jan./Dec. 1998
LINEARIZATION OF A GENERALIZED MATERIAL BALANCE EQUATION FOR COALBED METHANE RESERVOIRS
ABSTRACTT
A generalized material balance equation was presented at the Escuela de Petróleos de la Universidad Industrial de Santander for coal seam gas reservoirs based on Walsh 's method, who worked in an analogous approach for oil and gas conventional reservoirs (Walsh, 1 995). Our equation was based on twelve similar assumptions itemized by Walsh for his generalized expression for conventional reservoirs, it was started from the same volume balance consideration and was finally reorganized like Walsh (1 994) did. Because it is not expressed in terms of traditional (P/Z) plots, as proposed by King (1 990), it allows to perform a lot of quantitative and qualitative analyses. It was also demonstrated that the existent equations are only particular cases of the generalized expression evaluated under certain restrictions. This equation is applicable to coal seam gas reservoirs in saturated, equilibrium and undersaturated conditions, and to any type of coalbeds without restriction on especial values of the constant diffusion.
Keywords: coalbed methane, adsorption, langmuir isotherm.
RESUMEN
En la Escuela de Petróleos de la Universidad de Santander se presentó una ecuación generalizada de balance en materiales para yacimientos de gas asociado al carbón teniendo como punto de partida el método aplicado por Walsh, quien trabajó en una expresión similar pero para yacimientos convencionales de petróleo y gas (Walsh, 1995). Esta ecuación se fundamentó en doce suposiciones similares a las hechas por Walsh en su expresión generalizada para yacimientos convencionales, parte de la misma consideración volumétrica y finalmente se reorganiza como lo realizaron Walsh et al (1 994). Al no ser expresada en términos de los gráficos (P/Z) planteado por King (1 990), da pie para hacer un mayor número de análisis cuantitativos y cualitativos. Además se mostró que las ecuaciones existentes son solo casos particulares de la generalizada evaluada bajo ciertas restricciones. Esta ecuación es aplicable a yacimientos en estado saturado, equilibrio y subsaturado, y para cualquier manto de carbón sin restricciones para valores especiales de la constante de difusión.
Palabras clave: metano en capas de carbón, adsorción, isoterma Langmuir.


INTRODUTION
Except for the small amount of free gas that is occasionally found in the cleat system of a coal seam and in solution in resident brine, natural gas, comprised predominantly of methane (95%-98%) exists as a monomolecular layer in an almost liquid state, adsorbed on the internal surfaces of the coal matrix (Metcalfe, et al., 1991).
Gases are retained in the micropore structure of coal by physical adsorption, which can be reversed by lowering the partial pressure of the adsorbed species. For coalbed methane, this generally translates as reservoir pressure since the partial pressure equals the total pressure for pure species. Once this gas is desorbed from the matrix, it diffuses to the cleat system and flows to the producing well according to Darcy's law (Figure 1).

Coal seam gas reservoirs may be found in three possible initial states (Figure 2): (A) Equilibrium, (B) Saturated and (C) Undersaturated conditions. In the lower portion of Figure 2, a Langmuir isotherm is shown. Point A, equilibrium state, occurs when the amount of adsorbed gas is equal to the amount given by the isotherm. When the system is in equilibrium, the amount of gas adsorbed by the coal is governed by the sorption isotherm. A pressure drop in the cleat system causes gas to desorb from the micropore surfaces and to diffuse into the macropores. During production, a free gas phase will be formed in the cleats. Point B, the saturated state is similar to the equilibrium state in terms of adsorbed volume; however, free gas is present in the cleat system. During production, the reservoir is retained in the saturated condition. The third possibility, as described in Point C, is the existence of an undersaturated condition. In a coalbed reservoir described in point C, the amount of gas adsorbed into the coal is less than the amount depicted by the isotherm at reservoir pressure and temperature. In this case, no gas can be produced until its critical desorption pressure has been reached. As production and pressure decrease over the course of time, it enters the saturated condition.

The upper portion of Figure 2 shows gas saturations in the secondary porosity system (fracture system) for the aforementioned cases. For cases A and C, there is no initial free gas; hence gas saturation is marked as zero. For case B, the gas phase saturation is larger than zero.
In order to face the development of a material balance equation, the first step was to define what is a coal seam gas reservoir, how it behaves under different scenarios and what methods exist to compute reserves, as well as the properties than can be used to estimate them. Afterwards, it was necessary to determine its deduction and linearization.
MATERIAL BALANCE EQUATION
One of the fundamental principles utilized in engineering work is the law of conservation of matter. The application of this principle to hydrocarbon reservoirs with the purpose of quantify and predict is expressed by the material balance method.
Generalized Material Balance Equation for Conventional Reservoirs (GMBE)
Walsh (1994), developed a generalized material balance equation (GMBE) which is applicable to the full range of conventional reservoir fluids, including volatile-oil and gas-condensates. The mathematical development was based on the following assumptions or idealizations:
- The reservoir is an isothermal system.
- The reservoir is comprised of, at most, four components: rock, water, stocked tank oil and surface gas.
- The reservoir is comprised of, at most, four phases: rock, water (aqueous), oil and gas.
- The surface gas component exists only in the oil and gas phases and does not partition into the water or rock phases. This assumption allows for dissolved-oil.
- The stock tank oil component exists only in the oil and gas phases and does not partition into the water or rock phases. This assumption allows for volatilized oil.
- The water component exists only in the water phase and does not partition into either the oil, gas, or rock phases.
- The rock component exists only in the rock phase.
- The water and rock-phases are incompressible. This assumption implies the reservoir pore volume is constant.
- The reservoir pressure is uniform throughout the reservoir, i.e., no pressure gradients exist vertically or horizontally.
- The reservoir fluids are in thermodynamic equilibrium.
- Water may enter the reservoir, i.e., water influx may occur.
- Water, stock tank oil and surface gas components may be produced.
- The produced fluids may be reinjected into the reservoir.
- The porosity and initial water saturation are uniform throughout the reservoir.
The GMBE for conventional reservoirs is (Walsh, 1994):

Material balance equation for coal seam gas reservoirs (CMBE for CSG)
The assumption of non-reactive gas-rock makes the use of traditional equations inappropriate for CSG reservoirs, due to the large internal surface area contained within the coal seam, allowing many potential sorption sites to exist and where large quantities of gas may be adsorbed.
King (1990) presented the development of two material balance methods, the first one is appropriate for estimating gas in-place while the second one is useful for making future reservoir predictions. In spite the fact that these expressions are derived using the traditional assumptions associated with the material balance approach, the first one required an additional assumption of equilibrium between the free and adsorbed gas phases.

where:

The second proposed expression is less restrictive and it can be obtained by considering a gas desorption term, Gd . This equation has the form:

Generalized Material Balance Equation for Coal Seam Gas Reservoir (GMBE for CSG)
The following assumptions are used (Ordóñez y Peñuela, 1996):
- The reservoir is an isothermal system.
- The reservoir is comprised of, at most, three components: coal seam, water and surface gas.
- The reservoir is comprised of, at most, three phases: coal seam, water (aqueous) and gas.
- The surface gas component exists only in the coal and gas phases. This assumption allows for adsorbed gas.
- The water component exists only in the water phase and does not partition into either the coal or gas phases.
- The coal component exists only in the coal phase.
- The water and rock phases are compressible. This assumption implies the reservoir pore volume is a function of the pressure.
- The reservoir pressure is uniform throughout the reservoir, i.e., no pressure gradients exist vertically or horizontally.
- The reservoir fluids are in thermodynamic equilibrium.
- Water may enter the reservoir, i.e., water influx may occur.
- Water and surface gas components may be produced and/or injected.
- The porosity and initial water saturation are uniform throughout the reservoir.
Considering adequate volume balances (Appendix A), the GMBE for CSG can be written as:

LINEARIZATION OF THE MATERIAL BALANCE EQUATION
The linearization requires the plotting of a variable group vs. another variable group, with the variable group selection depending on the present production mechanism of the reservoir. The sequence of the plotted points and the shape of the resulting plot are important. Havlena and Odeh (1963), developed the popular straightline method for oil reservoirs. Walsh (1994) presented a general straightline method for estimating reserves of oil and gas reservoirs without restrictions on reservoir fluid compositions. This work was based on the GMBE recently developed by Walsh.
Linearization of the GMBE for oil-gas conventional reservoirs.
Walsh et al.(1995) rearranged the GMBE and proposed the following form:

where Nƒoi and Gƒgi are constant and equal to:


F, Eo, Eg and ΔW are functions of the pressure and are defined by:




The results of their work were summarized in a set of companion papers. The first one presents the mathematical development and discusses applications to initially undersaturated, volumetric reservoirs (Walsh et al., 1994). The second one discusses applications to initially saturated and non volumetric reservoirs (Walsh, 1994).
Linearization of the CMBE for CSG reservoirs
In this case the CMBE for CSG has the familiar form (King, 1990):

where in the general case, the modified Z-factor is defined by:

Linearization of the GMBE for CSG reservoirs
The GMBE conveniently rearranged has the following form:
where G is the SCF of adsorbed gas originally in the coal seam and G2i is the m3 of free gas originally in the secondary porosity system at standard conditions (298.15 K y 101.325 kPa). Eg1 expresses the desorption and adsorbed gas expanding effect with the consecutive pressure depletion and Eg2, represents the combined effects of gas, water and coal expansion.
F, Eg1, Eg2 and ΔW are defined by:




As for simulated, the equation (17) is especially appropriated, for initially saturated reservoirs (Swi<1). However in most cases it is necessary to dewater the coalbed, during a certain time, in order to produce gas from it. These reservoirs, in an undersaturated state (Swi= 1 ), have a Pi >Pd pressure. The initially equilibrium reservoir can be understood like a particular case of the undersaturated reservoirs because their fracture system is 100% saturated with water upon discovery (Swi = 1). Performing GMBE for CSG (Equation 17) in this case, presents a mathematical indetermination and hence it is necessary to do an algebraic manipulation before applying it. The GMBE adjusted to initially undersaturated reservoirs is defined as:

where F is the m3 of net gas withdrawal (net production) and G is the adsorbed initial gas in-place in the coal seam. Eg represents the gas, water and coal expansion net effect. This term can be written as:

EXAMPLES
Three validation examples were designed. The first one demonstrated that existent equations are only particular cases of the generalized equation evaluated under certain restrictions. Because the equations shown by King yield about 6% error in comparison with a finite difference simulator, this percentage would be the greatest error shown by GMBE for CSG in the worst of the cases. This example will be deferred to a subsequent writing.
In the second example it is demonstrated that the developed approach has the same properties of linearization like their conventional reservoir counterpart, i.e., it can be conveniently manipulated in order to analyze different important aspects, for instance, the estimation of the initial reserves (Figures 3 and 4).


In the third example as shown in Figure 5, using the GMBE for linearized CSG by means of a comparison against results given in the literature (King, 1990), it was concluded that the greatest effect of the desorption phenomenon occurs during the dewatering, as shown in the initial part of the plot presented in Figure 6. It is therefore necessary to have a good knowledge of both the dewatering phase and the properties that affect the desorption term, whose important effect is seen at earlier times of the production. Tables 1 and 2 give the petrophysical and sorption properties, the PVT and production data required to plot Figure 5 of the third example. Figure 6 shows the same data of Figure 5, but without adjusting the water production, as they appear in the reference paper (King, 1990).




CONCLUSIONS
- The GMBE developed in this paper can be applied to coalbed methane reservoirs in saturated, equilibrium, and undersaturated states. Once linearized, graphic procedures can be applied to analyze the behavior of the reservoir like it has been done for oil and gas reservoirs.
- The desorbed gas to the cleat system (secondary porosity system) can be seen like gas injection that comes from the same seam.
- The presentation of the generalized equation for CSG allows rearrangement and linearization. It is based on 12 assumptions similar to those itemized by Walsh in his generalized expression for oil and gas conventional reservoirs. It starts from the same volumetric considerations and it is finally reorganized like that of Walsh et al.
- The GMBE for CSG is not expressed in terms of traditional (P/Z) plots proposed by King, it allows substantial quantitative and qualitative analysis.
- The desorption and diffusion evidently affect the efficacy of the linearization especially in reservoirs that need a period of dewatering.
- This work is given as a tool in the study, comprehension and analysis of unconventional gas reservoirs and as an innovative way to teach reservoir engineering
- The contribution made by this paper is similar to work done by:
- King (1990), with the purpose to provide basic tools to engineers working with unconventional gas reservoirs.
- Walsh (1995), with the purpose to develop a generalized equation.
- Walsh et al. (1994), with the purpose to use a straight-line method and show graphic analysis of the most important reservoir aspects.
- Example 3 was worked with literature data and assumed appropriate cumulative water production. The application of reported data in the graphic analysis for the produced water did not yield a straight line in the zone where desorption dominates (dewatering period). Therefore application of the linearized GMBE for CSG is recommended for studying this behavior. Future work should include field data for different scenarios of gas production, water injection and gas injection.
ACKNOWLEDGEMENTS
The authors wish to thank the Universidad Industrial de Santander for its permission to publish this work and to the Instituto Colombiano del Petróleo (Ecopetrol-ICP) for the information and encouragement to develop it. We also wish to thank J.P. Seidle for his helpful comments.
REFERENCES
Almisned, O. A. and Thrasher R. L, 1995. "Simulation of Coalbed Methane Enhanced Recovery Using Gas Potential and a New Saturation Equation", Paper 9560 INTERGA'95, May 15 -19. [ Links ]
Havlena, D. and Odeh. A. S., 1963. "The Material balance as an Equation of a Straight Line", J. Can. Pet. Tech, Aug, Trans, AIME 228: 896 -900. [ Links ]
King, G. R, 1990. "Material Balance Techniques for Coal Seam and Devonian Shale Gas Reservoirs", Paper 20730 , SPE Annual Technical Conference and Exhibition, New Orleans, LA, September 23 -26. [ Links ]
Kohler, T. E. and Turgay, E., 1995. "Modeling of Undersaturated Coal Seam Gas Reservoir", Paper SPE 29578 presented at the SPE Rocky Mountain Regional/Low-permeability Reservoirs Symposium, Denver, March 20 -22. [ Links ]
Metcalfe, R. S., Yee, D., Seidle, J. P. and Puri, R. , 1991. "Review of Research Efforts in Coalbed Methane Recovery", Paper SPE 23025 presented at the SPE Asia-Pacific Conference, Perth, Western Australia, Nov 4 -7. [ Links ]
Ordóñez R, A. y Peñuela P. Gh., 1996. "Desarrollo y Linealización de una Ecuación de Balance de Materiales Generalizada para Yacimientos de Gas Asociado al Carbón", A Proyecto de Grado Escuela de Ingeniería de Petróleos, Universidad Industrial de Santander, Bucaramanga. [ Links ]
Pérez, P., Ramiro y Marcias J. Martínez. 1994. "Ingeniería de Gas Natural. Curso Características y Comportamiento de los Hidrocarburos, capitulo 1". Características de los Hidrocarburos Determinación del Factor de Compresibilidad Z., Método de Yarborough-Hall, Talleres Gráficos Germore C.A., Maracaibo-Venezuela. Julio p. 58. [ Links ]
Walsh, M. P, 1995. "A Generalized Approach to Reservoir Material Balance Calculations", Presented at the International Technical Conference of Petroleum Society of CIM, Calgary, Canada, May 9 -13. [ Links ]
Walsh, M. P., Ansah J. and R. Raghavan, 1994. "The New Generalized Material Balance as an Equation of a Straight Line: Part 1. -Applications to Undersaturated and Volumetric Reservoirs", Paper SPE 27684 presented at the 1994 Society of Petroleum Engineers Permian Basin Oil and Gas recovery Conference, Midland, TX. March 16 -18. [ Links ]
Walsh, M. P., 1994. "The New Generalized Material Balance as an Equation of a Straight Line: Part 2. -Applications to Saturated and Non-volumetric Reservoirs", SPE 27728 presented at the 1994 Society of Petroleum Engineers Permian Basin Oil and Gas Recovery Conference, Midland, TX. March 16 -18. [ Links ]
APPENDIX A
Derivation of the generalized material balance equation (GMBE) for CSG reservoirs.
This appendix derives the generalized material balance equation (GMBE for CSG) and expresses it as an equation of a straight line.
The mathematical development is based on the 12 aforementioned assumptions. Following these assumptions, a volume balance in the secondary-porosity system demands:
Figure 7 presents the CSG components involved in the material balance which are going to account during algebraic developments in this appendix.

The material balance (Figure 8) on the gas component in the fracture system demands:
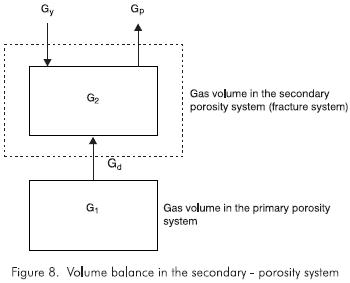
If Vb2 is the bulk volume of the secondary-porosity system then:
Substituting (A.2) and (A.3) into (A.1), rearranging and defining:
and
yield:
For secondary-porosity volume, one can initially find:
Substituting (A.7) in (A.6) and rearranging yields:
Literature shows the following porosity equation (Almisned and Thrasher, 1995)

For the sake of simplicity and brevity, we assume Cm≈ 0:
This expression is traditionally used in material balance. Substituting (A.10) into (A.8) and rearranging yields:
Although the term Gd can be obtained in literature (equations (5) and (6)) it is necessary to reproduce its physical meaning, in order to adjust it, as it can be seen later on. Starting with Fick's first law (by assuming pseudo-steady state flow):

leads to an equation that can be discretized:
This equation may be more easily understood by keeping in mind that the Fick's first law describes the phase movement of the free gas in the primary-porosity system because of the concentration gradient.
To better understand the discretized equation, a global vision of Fick's law can be considered. The gas available to diffuse through the primary-porosity system and to arrive in the seam's cleat (uniformly spaced natural fractures) is the gas of the primary non -adsorbed porosity (Vb2(G1-VE)).
The net variation of gas in the primary porosity system will be Gd The velocity at which gas volume decreases in the primary porosity system is proportional to the desorpted gas amount at this time.
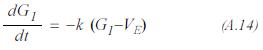
Taking k=Da one has equation (A.13). This equation is subject to the initial condition:

By definition, VE only depends on the pressure system, since the pressure may vary through time (as fluids are produced or injected), the differential equation with the above initial condition has the following formal solution:

Since Gd was previously stated as the net variation of gas in the primary-porosity system, then:
Substituting (A.17) in (A.11), yields:

Conveniently defining:
One can obtain the linearized expression:
By substituting the equations (A.4), (A.5), (A.19) and (A.20) in (A.22) yields:
and if Cm is not ignored, the above expression can be put into the form:

Initially undersaturated reservoir of the CSG
Equation (A.23) is the GMBE for CSG and as presented, it describes the fluid behavior of the initially saturated reservoirs (Swi<1). Nevertheless it presents a mathematical indetermination when applied to initially undersaturated reservoirs (Swi=1). To avoid this situation, this approach was rearranged.
Substituting (A.7) into (A.23), yields:
Using the definition of on initially undersaturated reservoir, i.e., all initial gas to a P>Pd is totally adsorbed in the coal seam and hence in the cleat system (Swi=1), the expression is then:

Substituting (A.21) into (A.25) and rearranging, yields:

which can be written as:

by conveniently defining:

and if Cm is not ignored, the above approach becomes:




































