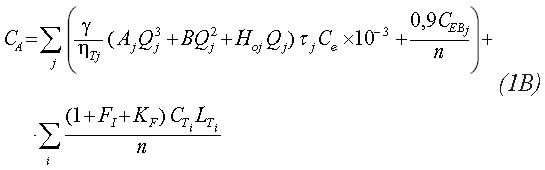Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.2 no.4 Bucaramanga Jan./Dec. 2003
GENETIC ALGORITHMS FOR THE OPTIMIZATION OF PIPELINE SYSTEMS FOR LIQUID TRANSPORTATION (1)
Haiver Galeano*1 and Paulo–César Narváez*2
1 P y P Construcciones S.A. – Departamento de InformaciónTecnológica, Bogotá, Colombia
2 Universidad Nacional de Colombia – Departamento de Ingeniería Química, Bogotá, Colombia
e–mail: haiver.galeano@pyp.com.co e–mail: pcnarvaezr@unal.edu.co
(Received 14 August 2003; Accepted 20 November 2003)
*To whom correspondence may be addressed
ABSTRACT
This is the first of two articles in which a Genetic Algorithm (GA) is presented to obtain an optimal design of a pipeline system for liquid transportation, from an economical and operational point of view. This GA is based on criteria such as compliance with the laws of matter and energy conservation; flow requirements in consumption points where pressure is known; restrictions to the pressure value in system points where pressure is unknown, and to the velocity, which must be lower than the erosion limit velocity.
This article combines traditional techniques for the design of GA in this type of problems with some ideas that had never been applied before in this field. The proposed GA allows sizing of the liquid distribution systems, including pipelines, consumption and supply nodes, tanks, pumping equipment, nozzles, control valves, and accessories.
This article includes different formulations found in literature on network design through optimization techniques and carries out the mathematical formulation of the optimization issue. In the second article the characteristics of the designed Genetic Algorithm (GA) are specified and further applied to the issues presented by Alperovits and Shamir (1977), and Fujiwara and Khang (1990), addressing the water distribution network at Hanoi, in Vietnam . Finally, the GA is applied to a fire protection network, allowing for the testing of some of the model’s characteristics which are not reported in the pertinent literature, such as the possibility to include pumping equipment, aspersion nozzles, and accessories.
Keywords: optimization, genetic algorithms, fluid distribution networks, pipe networks.
RESUMEN
Este es el primero de dos artículos en los que se presenta un Algoritmo Genético (AG) para obtener un diseño óptimo de un sistema de tuberías para el transporte de líquidos, desde el punto de vista económico y de operación, con base en criterios tales como el cumplimiento de las leyes de la conservación de la masa y la energía, exigencias de caudal en los puntos de consumo en donde se conoce la presión, restricciones en el valor de la presión en los puntos del sistema en donde se desconoce y en la velocidad, que debe ser inferior a la límite de erosión.
En él se combinan las técnicas tradicionales para el diseño de AG en este tipo de problemas, con algunas ideas que no se habían aplicado con anterioridad en este campo. El AG propuesto permite el dimensionamiento de sistemas de distribución de líquidos que incluye tuberías, nodos de consumo y suministro, tanques, equipos de bombeo, boquillas, válvulas de control y accesorios.
En este artículo se presentan las diferentes formulaciones que se encuentran en la literatura para el diseño de redes mediante técnicas de optimización y se hace la formulación matemática del problema de optimización. En el segundo artículo se especifican las características del Algoritmo Genético (AG) diseñado y su aplicación sobre los problemas presentados por Alperovits y Shamir (1977), y Fujiwara y Khang (1990), que corresponde a la red de distribución de agua de la ciudad de Hanoi en Vietnam. Finalmente se aplica el AG a una red contra incendio, lo que permite probar algunas de las características del modelo que no se encuentran en los reportados en la literatura, como son la posibilidad de incluir equipos de bombeo, boquillas de aspersión y accesorios.
[keygrp scheme=decs]Palabras claves: optimización, algoritmos genéticos, redes de distribución de fluidos, redes de tuberías.
RESUMEN
Este é o primeiro de dois artigos nos que se apresenta um Algoritmo Genético (AG) para obter um desenho ótimo de um sistema de tubulações para o transporte de líquidos, desde o ponto de vista econômico e de operação, com base em critérios tais como o cumprimento das leis da conservação da massa e a energia, exigências de caudal nos pontos de consumo onde se conhece a pressão, restrições no valor da pressão nos pontos do sistema onde se desconhece e na velocidade, que deve ser inferior ao limite de erosão.
Nele se combinam as técnicas tradicionais para o desenho de AG neste tipo de problemas, com algumas idéias que não se tinham aplicado com anterioridade neste campo. O AG proposto permite o dimensionamento de sistemas de distribuição de líquidos que inclui tubulações, nodos de consumo e subministro, tanques, equipamentos de bombeio, boquilhas, válvulas de controle e acessórios.
Neste artigo apresentamse as diferentes formulações que se encontram na literatura para o desenho de redes mediante técnicas de otimização e fazse a formulação matemática do problema de otimização. No segundo artigo especificamse as características do Algoritmo Genético (AG) desenhado e a sua aplicação sobre os problemas apresentados por Alperovits e Shamir (1977), e Fujiwara e Khang (1990), que corresponde à rede de distribuição de água da cidade de Hanoi no Vietnam. Finalmente se aplica o AG a uma rede contra incêndio, o que permite provar algumas das características do modelo que não se encontram nos reportados na literatura, como são a possibilidade de incluir equipamentos de bombeio, boquilhas de aspersão e acessórios.
NOMENCLATURA

INTRODUCTION
Computer programs for fluid distribution systems have become a very popular tool for the analysis and design of such systems. These programs run on models that allow the following, among others:
– To simulate different diameters and system configurations, to determine the combination that may deliver fluids at the required pressure and flow conditions at the consumption points.
– To simulate flows and pressures with different operating pumping equipments, to carry out a proper selection.
– To simulate the system’s operating conditions for different storage tank levels, to define the maximum and minimum permissible levels.
– To simulate the tank level fluctuations within a period, as a response to variations in consumption, to evaluate the different pumping strategies, and thus to determine the best operating conditions.
– To recommend the pipeline diameters to be used, taking into account cost minimization, under given restrictions.
Models may be classified in two groups: those that allow simulation of the distribution system, and those that use optimization theories.
The first models predict pressures and flows, and may even calculate levels in a tank as a function of time. Users of these models look for determine the most suitable dimensions for pipelines, through a trial–and–error process, in which an engineer tests different network components, executes simulations and carries out a comparison of the calculated values against the required ones, in order to take the decision to modify the network. A cost estimative for each feasible alternative is performed from a technical point of view to take the final decision.
Models based on optimization theories allow to obtain solutions that correspond to the minimum of a non–linear, highly structured and restricted optimization problem.
Designing and operating a pipeline system for fluid distribution are common and critical tasks in the oil and gas industry. Oil pipelines, gas pipelines, industrial services distribution networks in refineries and other chemical transformation plants, fire protection networks, residential water supply and natural gas networks, must be all designed to comply with the flow and pressure needs at the consumption points, and with a combination of pipeline diameters, and pumping and/or compression systems at a minimum cost (taking into consideration initial investment in pipelines, accessories and equipment, as well as operation costs, which are translated into pumping and/or compression and maintenance costs). The genetic algorithm presented in this paper is a tool for the design and optimization of pipeline systems for liquid distribution which allows reducing the man hours invested in carrying out the hydraulic calculations and exploring a larger number of alternatives.
General characteristics of the techniques for the solution of optimization problems in fluid distribution systems are shown below and are further compared to one another, to formulate the optimization problem that must be resolved with the genetic algorithm.
SOLUTION TECHNIQUES FOR OPTIMIZATION PROBLEMS IN FLUID DISTRIBUTION SYSTEMS
The optimal design of fluid distribution systems must consider several aspects, such as its behavior from the point of view of fluid mechanics, service standards, its reliability, the quality of the fluid, and consumption schemes (Gessler, 1989). In simple terms, the designing problem for a fluid distribution system consists of finding the most cost–effective combination of network components for a given pipeline outline, subject to the following conditions:
–Flow continuity must be maintained in each of the network’s nodes or unions.
–The loss of energy by friction in each pipeline is a known function of the respective flow, diameter, length and corrugation.
–The set of pumping equipment and storage tanks available or to be designed.
The solution for this problem is difficult, due to the non–linear relation of the flow with energy losses or gains; to the presence of discrete variables, such as commercial pipeline diameters; and to the large size of the searching space.
Due to the problem’s complexity, several techniques have been used to simplify the search of a solution. The methods employed are based on enumerative techniques, on mathematical programming (linear and non–linear) and on stochastic methods (genetic algorithms).
Enumeration
Enumeration is an approach to the optimization of fluid distribution systems in which all the possible combinations of discrete pipeline sizes are simulated, and the most economic network design that satisfies the hydraulic restrictions is selected (Walski, 1990). The main inconvenience this technique presents is the length of computing time required. For example, in a relatively small system with 20 pipelines of 10 possible discrete sizes, nearly 1020 solutions must be simulated. If one million designs could be evaluated every second, it would take three million years of calculations to carry out the whole enumeration (Simpson, 1994).
For this reason and while based on the designer experience, Gessler (1989) proposed the use of selective enumeration in a highly trimmed search space, through which the global optimum value could be excluded from the alternatives. Even with the use of techniques proposed by several authors (Simpson, 1994), a large amount of computing time is required, with no guarantee that the optimum value will remain within the search space.
Mathematical programming
A great number of researchers have used mathematical programming to optimize the design of fluid distribution networks. The main project in this area was presented in 1977 by Alperovits and Shamir (Alperovits, 1977), who proposed a method called Linear Programming by Gradient (LPG) through which an optimal design may be obtained.
Linear programming
The linear programming procedure is based on the special selection of decision variables. Instead of selecting pipeline diameters, a set of potential diameters is used in each connection. Selection variables are the segment lengths of each diameter in the connection.
Energy losses due to friction in each connection correspond to the summation of the product between the hydraulic gradient (losses by length unit) and the length of each segment of a given diameter. The cost of pipelines is assumed as a function directly proportional to the length. Minimizing this cost’s linear function, as subject to pressure restrictions in each network node and to the non–negativity condition of the segment lengths, becomes the linear problem.
This technique has been one of the most studied and favorable results have been obtained in mid–sized networks with acceptable convergence times. Advantages include operation conditions that are explicitly introduced into the design process. The solution is feasible from the fluid mechanics point of view and allows the easy introduction of pumps, valves and tanks. On the other hand, inconveniences include the following:
The solution is a global – optimum for each selection of decision variables and, considering all the possible decision variable's combinations, the optimum is just local, forcing the optimization process to start from several points.
An initial assumption for – flow distribution which complies with balance of matter must be made, causing a time–consuming process for the designer.
Generally, the solution – consists of two or more segments of pipeline with different diameters between each pair of nodes, a fact that is undesirable in any real, substantially sized design.
The search procedure – requires several heuristic rules which may only be acquired through experience.
All equations that must be – incorporated to enable handling of pumps, control valves, tanks and improvements to the cost equation shall be manipulated to retain linearity, forcing to make assumptions which diminish the accuracy and reliability of the system.
Non linear programming
A number of non–linear optimization programs may be applied to solve the fluid–distribution system design problems, including MINO, GINO, GAMS and GRG2 (Landson et al., 1984), which use the generalized reduced gradient technique to identify the local optimal value, with continuous variables to simulate the system parameters.
The solution technique is based on the concepts of the optimal control theory, in which the generalized reduced gradient method is in charge of the overall optimization problem, which is supported by the simulation model that carries out assessments for each iteration (Landsey and Mays, 1989). In other words, the highly non–linear problem is solved by reducing the complexity through the incorporation of a fluid–distribution system simulator that implicitly solves the restrictions on flow and energy conservation. The following are some of the method–related disadvantages:
The optimal values do not – correspond to commercially available diameters, since these are considered to be a continuous variable within the model.
Only local optimal values – are achieved.
The network size is – restricted as per the number of restrictions.
It is necessary to acquire – a commercial linear programming tool, featuring high mathematical sophistication, although designed for a general purpose. This implies the need to adapt it.
Genetic Algorithms (GA)
A GA is a search procedure based on natural selection, genetic population mechanisms and survival and adaptation biological processes. The result is an efficient algorithm with the flexibility to search in complex spaces, like the one found while designing a fluid distribution network.
GAs have numerous advantages over other optimization techniques, like the ones shown below (Savic and Walter, 1997; Montesinos et al., 1996):
GAs directly consider a – population of solutions every time, enabling the search to be extended across the solution space, in such a way that the probability to encounter a global optimal value is greater to that for mathematical programming techniques.
Each solution consists of a – set of pipeline’s discrete sizes.
GAs identify a set of – solutions that are close to that with minimal cost. These solutions may correspond to designs that differ slightly from one another and that may be compared to evaluate important non–quantitative variables.
GAs on –ly require information on the objective or fitness function – a difference from other techniques that need additional information.
However, GAs do not guarantee the optimal global solution to be found; although, experience has shown that a good approximation may be achieved through a reasonable number of evaluations. Calculation times are one of the main inconveniences of this technique, being greater than those required in mathematical programming.
The optimization procedure with GAs involves the following steps (Dandy et al., 1996; Savic and Walters, 1994; Montesinos et al., 1996; Simpson et al., 1994; Savic and Walters, 1997):
Initial population generation
The GA generates the starting population with size N, between 100 and 1000, with a random number generator, where each of the N individuals represents a different configuration for the pipeline system.
Network cost calculation
The GA considers each of the N individuals from the population in turn. The algorithm decodes each individual in its corresponding set of pipeline sizes, and calculates the system’s total cost.
System’s mathematical model
To calculate pressure and flow values, any mathematical model and any fluid–distribution systems solution method in steady state is used. The values of these variables are compared against the required values.
Penalty costs calculation
The GA assigns a penalty value if the network does not meet the problem’s restrictions. The difference between the calculated value and the required one is used as the basis for this calculation. This difference is multiplied by a penalty factor k, which is empirically defined and which measures the cost for non–compliance with the restriction.
Network total costs calculation
This includes the network costs, plus the penalty costs.
Fitness function calculation
This function depends on the target costs function. The GA searches the minimum cost configuration, which implies the target function to be minimized. Therefore, the fitness function guarantees that the lower cost idividual will survive and shall correspond to the inverse of the total network cost.
New population generation
The GA generates new members for the next generation through a selection scheme. Frequently, the proportional selection method known as the roulette is used in such a way that the individuals with larger adjustments have a greater probability of selection.
Crossing operation
Crossing is a partial change in the components of two parent individualss to form two daughter individuals. The GA randomly selects two individuals from the population to perform the crossing. Afterwards, the individual point where the exchange takes place is randomly selected.
Mutation operation
Ideally, the mutation operation should guarantee that no part of the genetic material is lost; however, this type of operator does not achieve such goal. The mutation operator changes the value of the individuals components for their opposite value; that is, from 0 to 1, and vice versa.
Successive generation production
In this step, a new generation is produced through the use of crossing and mutation operations. The GA repeats the process described above to produce successive generations.
OPTIMIZATION TECHNIQUES COMPARISON
From the designing engineer’s point of view, the analysis of the optimization techniques advantages and disadvantages show that the following aspects should be considered:
–The complete enumeration technique is not feasible for the resolution of the typical problems a designer has to face, since the calculation times are too long, even for small systems.
–Optimal solutions found through the linear programming technique are inconvenient, since they divide portions usually constructed with a single diameter pipeline into segments of different diameters, requiring the execution of additional calculations. Furthermore, the need to make an initial volume estimate that complies with the matter balance, forces the designer to use resources to introduce data that has no meaning at all.
–In non–linear programming it is essential for the diameter to be a continuous variable, an unavoidable handicap from a practical point of view, since the designer must approximate the diameter values to the ones commercially available and recalculate
the system.
–The major drawback of GA involves calculation times, which are greater than the ones for mathematical programming techniques. However, times reported in literature are shorter than those required for the design of a system without a tool like this one. Additionally, GA work directly on the fluid mechanics phenomenon without limiting it with the impact of the optimization technique.
PROBLEM FORMULATION
The problem to be solved by the GA during the optimization of the pipeline systems for liquid distribution is described as follows:
A combination of diameters and pumping systems at a minimal cost for pressure and flow conditions at the nodes, and velocity for each pipeline, shall be defined for a given pipeline layout, taking into consideration the initial investment in pumping equipment and pipelines, plus the system’s operating costs, as translated into pumping and pipeline maintenance costs, stated in time units (Galeano, 2000).
This problem is subject to the following conditions:
–Flow continuity shall be kept in all network couplings or nodes.
–Total pressure losses1 through the loop shall be equal to zero; or, the energy loss through the path joining two deposits shall be equal to the available energy.
–The fluid velocity in the hydraulic system pipelines shall be less than the erosion limit velocity2.
–For nodes with known energy3, certain restrictions must be observed regarding volume as needed for such points of interest within the network.
–For nodes with unknown energy4, certain restrictions must be observed regarding working pressure.
–Some restrictions in maximum and minimum diameters are applicable to pipelines.
–The hydraulic system considered is made up of pipelines, supply or consumption nodes, pumps, control valves, aspersion nozzles, tanks, in–line equipment, and accessories.
1 Supposedly, the loss of pressure in each tube is a known function for the flow, for its diameter, its length, and all other hydraulic properties.
2 The erosion velocity is the minimum velocity at which the flow is able to drag the corrosion layer that protects the tube, leaving the surface exposed and allowing this process starts again, causing pipeline deterioration.
3 Those points of interest in which the pressure and height are known, but the flow is unknown.
4 Those points of interest in which the desired volume is known, but the working pressure is unknown.
The mathematical formulation of the problem regarding the optimization of the fluid distribution systems is stated as the minimization of the cost function, which depends on the diameter and length of each part of the pipeline, and of the pumping equipment within the system. In those cases in which the network accessories are known in detail, the annual cost of the system is given by (Narváez, 2002):
Where the first summation is calculated by considering all the network’s pumping systems, and the second summation is made for all the pipeline diameters used in the system.
In those situations in which no detailed information on the accessories is available, the system’s annual cost is calculated by:
In these equations, variables to be optimized are pipeline diameters in the network and pumping equipment to be used. This is due to the fact that the pipeline cost per linear meter CTi is a function of the diameter, and, that the system may operate with different pumping systems, each with specific characteristics (Aj, Bj, Hoj, Qj and CEBj).
The aforementioned function shall be minimized, considering the following restrictions.
1. For each node of the network, the continuity equation shall be enforced:
Where Qinput is the flow entering the node, Qoutput is the total flow exiting the node, and Qe is the external demand or supply of fluid at the connection point.
2. For each of the system’s loops, the energy conservation equation shall be enforced:
Where HB is the pumping energy supplied to the fluid, and hf is the pressure loss in each element.
3. Velocity restriction for each of the network’s pipelines may be stated as:
Where Vi is the fluid’s velocity in pipeline I, VLE is the erosion limit velocity, and VLS is the sedimentation limit velocity.
Equation 4 shows that pipelines should be designed so that the flow velocity is slower than a certain velocity at which problems such as erosion, noise and ram strike appear; and faster than another one, such that the pulsating flow is minimized and sand and other solids may be transported.
Erosion happens when drops of liquid hit the pipeline wall with enough strength to flake down corrosion products, in such a way that the wall is exposed again and the process has to be restarted. A direct ratio for the flow velocity and the tendency of a fluid to produce erosion shall exist, so that as the velocity increases, a higher erosion production tendency is observed. Experiments in biphasic flow have demonstrated that this phenomenon occurs when the velocity is higher than the erosion limit velocity, which may be calculated through the following equation ( Arnold, 1987):
Where C is an empiric constant that, according to The API Recommended Practice 14E, shall be 122 for continuous service and 152 for intermittent service. Fluid’s density shall be stated in kilograms per cubic meter, and velocity is measured in meters per second.
Lines that transport liquids are generally designed in such a way that velocity is high enough to avoid deposits of solid particles in the pipeline bottom. For example, if sand is being transported, it will deposit itself in this point until the fluid reaches a so called equilibrium velocity. From there on, sand will be removed from the bottom at the same velocity at which it is being deposited. Given the complexity of the behavior and the equations for the calculation of the equilibrium velocity, for most practical cases a minimum velocity of 1m/s is recommended.
4. Diameters allowed in each pipeline are restricted as follows:
Where Di is the pipeline diameter, Dimax represents the maximum diameter allowed, Dimin the minimum diameter allowed, and DC is the set of diameters commercially available, and R is the set of pipelines in the network.
5. For each node in the network where the pressure is unknown, the calculated pressure shall comply with the following restriction:
Where Pk is the calculated pressure in each node and Pkmax and Pkmin are the maximum and minimum pressures allowed in node k, and N is the set of nodes in the network.
6. The volume of water demanded from or supplied to each of the known–pressure nodes of the network shall comply with the restriction:
Where Qk is the volume calculated at each node and Qkmax and Qkmin are the maximum and minimum volumes allowed in node k.
CONCLUSIONS
In this article, the general bases to formulate the optimization problem in liquid–distribution pipeline systems are set. From the designer’s point of view, out of the three optimization techniques, the one that offers a better alternative is that of genetic algorithms. To design a genetic algorithm it is necessary to formulate the target function to be minimized. This corresponds to the fixed and operation costs equation, subject to the fulfilment of the mass and energy balances, and to some restrictions regarding pressure at nodes of unknown energy, volumes supplied or demanded at the nodes of known energy, commercial diameters, and erosion limit velocity.
BIBLIOGRAPHY
Alperovits, E. Y. and Shamir, U., 1997. "Design of optimal water distribution networks". Water Resources Research, 13 (6): 885-900. [ Links ]
Arnold, K. Y. and Stewart, M., 1987. "Surface production operations". Houston, Texas, Gulf Publishing Company. [ Links ]
Dandy, G. C., Simpson, A. R. and Murphy, L. J., 1996. "An improved genetic algorithm for pipe network optimization". Water Resources Research, 32 (2): 449-458. [ Links ]
Fujiwara, O. and Khang, D. B., 1990. "A two-phase decomposition method for optimal design of looped water distribution networks". Water Resources Research, 26 (4): 539-549. [ Links ]
Galeano, H., 2000. "Estudio e implementación de un prototipo de un sistema de optimización para el dimensionamiento de redes hidráulicas". Tesis de Maestría, Departamento de Ingeniería de Sistemas, Facultad de Ingeniería, Universidad Nacional de Colombia, 194 pp. [ Links ]
Gessler, A. and Shamir, U., 1989. "Analysis of the linear programming gradient method for optimal design of water supply networks". Water Resources Research, 25 (7): 1469-1480. [ Links ]
Landsey, K. E. and Mays, L. W., 1989. "Optimization model for water distribution system design". J. Hydraul. Engineer.. SCE, 115 (10): 1401-1418. [ Links ]
Lasdon, L. D., Waren, A. D. and Rater, M. S., 1984. "GRG User's Guide, University of Texas at Austin, tex, 1984". In: http://web.wt.net/wti/grg2.htm. [ Links ]
Montesinos, M. P., García-Guzmán, A. y Ayuso, J. L., 1996. "Optimización de redes de distribución de agua utilizando un algoritmo genético". Ingeniería del Agua, 4 (1): 71-77. [ Links ]
Narváez, P. C. y Galeano, H., 2002. "Ecuación de costos y función objetivo para la optimización del diseño de redes de flujo de líquidos a presión". Ingeniería e Investigación, 49: 23-29. [ Links ]
Savic, D. A. and Walters, G., 1994. "Sensitivity of optimal pipeline system design to changes in head loss equation". Report number: 94/21, Center for Systems and Control Engineering, University of Exeter, United Kingdom . [ Links ]
Savic, D. A. and Walters, G., 1997. "Genetic algorithms for least-cost design of waters distribution networks". J. Water Resourc. Plan. and Manag., 123 (2): 67-77. [ Links ]
Simpson, A. R., Dandy, G. C. and Murphy, L. J., 1994. "Genetic algorithms compared to other tecniques for pipe optimization". J. Water Resourc. Plan. and Manag., 120 (4): 423-443. [ Links ]
Walski, T. M., Gessler, J. and Sjostrom, J. W., 1990. "Water distribution systems: simulation and sizing". Chelsea, Michigan, Lewis Publishers. [ Links ]