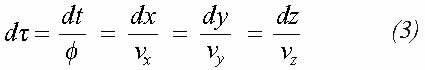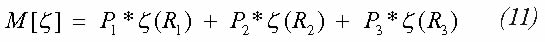RESUMEN

En este trabajo se presenta una metodología integrada para la predicción del comportamiento de producción de un yacimiento altamente heterogéneo sometido a inyección de agua cuantificando la incertidumbre asociada tanto en el marco de referencia estratigráfico como en el modelo petrofísico.

El enfoque clásico de este tipo de yacimientos presenta un manejo determinístico de la heterogeneidad asociada. Esto se constituye en un riesgo puesto que la estructura sedimentaria, las propiedades de las rocas y la distribución de las unidades de flujo en sistemas de depositación fluvial tienen una influencia primordial en el caso del recobro mediante inyección de agua y ese riesgo debe ser cuantificado de la manera más exacta posible para optimizar las inversiones pertinentes. La incertidumbre en este tipo de yacimientos se presenta no solamente en la distribución espacial de las propiedades petrofísicas en las unidades de flujo sino también en la distribución espacial de las unidades de flujo propiamente dichas.

La metodología propuesta involucra la evaluación de la incertidumbre asociada mediante clasificación jerárquica y selección de los modelos generados geoestadísticamente correspondientes a los cuantiles P₁₀, P₅₀ y P₉₀, con base en una variable indicadora del comportamiento del parámetro a evaluar. En la evaluación de la incertidumbre asociada al marco de referencia estratigráfico se utilizó como parámetro de jeraquización el porcentaje de yacimiento interconectado. La eficiencia volumétrica de barrido a un determinado tiempo, obtenida a partir del tiempo de vuelo de la simulación streamline, fue utilizada como la variable de clasificación jerárquica de los modelos petrofísicos.

En este trabajo presentamos la aplicación de la metodología propuesta a un caso real. El ejemplo se desarrolla en un piloto del Campo La Cira que incluye 3 pozos productores y 9 pozos inyectores, que conforman 3 patrones de inyección–producción. Los resultados obtenidos muestran el potencial de la técnica propuesta en el caso de un yacimiento como este en donde debido al ambiente de depositación fluvial se ha conformado una distribución compleja de canales de flujo, la cual dificulta la supervisión y predicción del comportamiento del yacimiento.

P₅₀ y P₉₀, con base en una variable indicadora del comportamiento del parámetro a evaluar. En la evaluación de la incertidumbre asociada al marco de referencia estratigráfico se utilizó como parámetro de jeraquización el porcentaje de yacimiento interconectado. La eficiencia volumétrica de barrido a un determinado tiempo, obtenida a partir del tiempo de vuelo de la simulación streamline, fue utilizada como la variable de clasificación jerárquica de los modelos petrofísicos.

En este trabajo presentamos la aplicación de la metodología propuesta a un caso real. El ejemplo se desarrolla en un piloto del Campo La Cira que incluye tres pozos productores y nueve pozos inyectores, que conforman tres patrones de inyección–producción. Los resultados obtenidos muestran el potencial de la técnica propuesta en el caso de un yacimiento como este en donde debido al ambiente de depositación fluvial se ha conformado una distribución compleja de canales de flujo, la cual dificulta la supervisión y predicción del comportamiento del yacimiento.

Palabras claves: inyección de agua, modelamiento geoestadístico, jerarquización, simulación streamline,caracterización de yacimientos, heterogeneidad del yacimiento, evaluación de incertidumbre, campo La Cira.

ABSTRACT

This paper focuses on an integrated methodology for the prediction of the production behavior of a highly heterogeneous oilfield subject to water injection, quantifying the related uncertainty in both, the stratigraphical reference framework and the petrophysical model.

The proposed methodology involves the evaluation of the related uncertainty through hierarchical classification and the selection of the geostatistically generated models corresponding to the P₁₀, P₅₀ and P₉₀ quantiles, based on a variable indicating the behavior of the parameter to be evaluated. In the evaluation of the uncertainty related to the stratigraphical reference framework, the percentage of interconnected oilfield was used as a hierarchy definition parameter. The sweeping volumetric efficiency at a certain time, as obtained from the flight time of the streamline simulation, was used as the hierarchical classification variable for petrophysical models.

This paper shows the application of the proposed methodology to a real case. The example is carried out within a pilot project at the La Cira Field, which includes three productive wells and nine injecting wells, making up three injection–production patterns. Results show the potential of the proposed technique in the case of an oilfield like this one, in which a complex distribution of flow channels has been conformed due to fluvial deposits, thus discouraging supervision and prediction of the oilfield’s behavior.

Keywords: waterflood, geoestatistical, ranking, streamline simulation, reservoir description, reservoir heterogeneities, uncertainty evaluation, La Cira Field.

RESUMEN

Neste trabalho apresenta–se uma metodologia integrada para a predição do comportamento de produção de uma jazida altamente heterogênea submetida à injeção de água quantificando a incerteza associada tanto no marco de referência estratigráfico como no modelo petrofísico.

O enfoque clássico deste tipo de jazidas apresenta um manejo determinístico da heterogeneidade associada. Isto se constitui em um risco posto que a estrutura sedimentária, as propriedades das rocas e a distribuição das unidades de fluxo em sistemas de depositação fluvial têm uma influência primordial no caso do recobro mediante injeção de água e esse risco deve ser quantificado da maneira mais exata possível para otimizar os investimentos pertinentes. A incerteza neste tipo de jazidas apresenta–se não somente na distribuição espacial das propriedades petrofísicas nas unidades de fluxo senão também na distribuição espacial das unidades de fluxo propriamente tais.

A metodologia proposta envolve a avaliação da incerteza associada mediante classificação hierárquica e seleção dos modelos gerados geoestatísticamente correspondentes aos quantis P₁₀, P₅₀ y P₉₀, com base em uma variável indicadora do comportamento do parâmetro a avaliar. Na avaliação da incerteza associada ao marco de referência estratigráfico utilizouse como parâmetro de hierarquização a porcentagem de jazida interconectada. A eficiência volumétrica de barrido a um determinado tempo, obtida a partir do tempo de vôo da simulação streamline, foi utilizada como a variável de classificação hierárquica dos modelos petrofísicos.

Neste trabalho apresentamos a aplicação da metodologia proposta a um caso real. O exemplo desenvolve–se em um piloto do Campo La Cira que inclui 3 poços produtores e 9 poços injetores, que conformam 3 padrões de injeção–produção. Os resultados obtidos mostram o potencial da técnica proposta no caso de uma jazida como este onde devido ao ambiente de depositação fluvial tem se conformado uma distribuição complexa de canais de fluxo, a qual dificulta a supervisão e predição do comportamento da jazida.

NOMENCLATURA

INTRODUCCIÓN

La estructura sedimentaria y las propiedades de las rocas clásticas en sistemas de depositación fluvial tienen una influencia trascendental en el recobro mediante inyección de agua. Este tipo de yacimientos desarrollan geometrías complejas a diferentes escalas, cortándose y superponiéndose unas a otras formando yacimientos altamente heterogéneos.

Ecopetrol en la Gerencia Centro–Oriente ha desarrollado varios proyectos de recuperación secundaria mediante inyección de agua; los cuales no han arrojado los resultados esperados en cuanto a producción y cálculo de reservas, lo que ha afectado la rentabilidad económica de los proyectos. Se ha observado que después de someter el yacimiento a un largo periodo de inyección de agua; la mayoría de los canales de arena han alcanzado un estado final de alto corte de agua. A pesar de esta situación se sabe que existe un volumen considerable de aceite residual; pero que debido a su compleja distribución se hace difícil ubicarlo y explotarlo adecuadamente.

Para desarrollar un modelo de predicción confiable para esta clase de yacimientos, es necesario una detallada descripción del mismo, que tenga en cuenta el efecto de las heterogeneidades y la influencia que éstas tienen en las eficiencias de barrido areal y vertical.

Los diferentes métodos existentes para la predicción del desempeño de yacimientos sometidos a inyección de agua difieren en el manejo que le dan a los parámetros involucrados en la determinación de: las heterogeneidades, el cálculo de la eficiencia de barrido areal, el comportamiento de la inyección de agua, la eficiencia de desplazamiento y otras variables que afectan el comportamiento de la inyección de agua. Estos métodos de predicción generalmente trabajan con un modelo único (determinístico) de las propiedades del yacimiento; sin considerar la incertidumbre asociada al modelo. Shoeppel (1968) y Craig (1971) resumen varios de los métodos publicados para la predicción del desempeño de la inyección de agua.

El incremento de recobro del aceite remanente en los yacimientos, requiere una buena práctica en el manejo de éstos, por consiguiente, la aplicación de tecnologías robustas de caracterización de yacimientos tienen un efecto directo en la eficiencia de recuperación de aceite.

El uso de las técnicas geoestadísticas para generar múltiples realizaciones tridimensionales de porosidad y permeabilidad están en constante aumento en la ingeniería de yacimientos. Los métodos geoestadísticos pueden generar imágenes de alta resolución de las propiedades del yacimiento, las cuales mantienen las heterogeneidades presentes en el yacimiento. Al considerar la variación existente de realización a realización se logra caracterizar la incertidumbre asociada a una información incompleta y/o a la falta de datos.

Cuantificar los impactos de la incertidumbre sobre los pronósticos de comportamiento del yacimiento, haría necesario la simulación de flujo para un gran número de estas posibles descripciones del yacimiento. Sin embargo, las limitaciones computacionales evitan a menudo el uso de la totalidad de los modelos geoestadísticos en los "pronósticos" del yacimiento. Generalmente, se usan sólo algunas realizaciones seleccionadas para las simulaciones detalladas, esto para proporcionar una medida del rango de incertidumbre en el comportamiento del yacimiento.

Las realizaciones geoestadísticas se seleccionan mediante la jerarquización (ranking) de los modelos estocásticos del yacimiento con base en una variable indicadora de comportamiento. Idrobo et al. (2000) proponen un nuevo criterio de jerarquización para modelos geoestadísticos que utiliza la conectividad del tiempo de vuelo de la simulación streamline, la cual proporciona una estimación directa de la eficiencia de barrido areal o volumétrico, pero para aplicaciones prácticas, es necesario extraer la información estadística (media y varianza) del comportamiento del yacimiento, mediante la ponderación apropiada de los resultados de la variable indicadora utilizada para jerarquizar las realizaciones.

Mishra y Kelley (2000) toman el planteamiento de Kaplan (1981) el cual establece que una distribución continua se puede reemplazar por una distribución discreta de tres valores. A las distribuciones discretas se deben ponderar mediante el cálculo de unos pesos, los cuales son obtenidos al aplicar un algoritmo que ajusta los momentos estadísticos y garantiza que se respete la media y la varianza de la distribución continua.

Este trabajo propone una metodología que parte de una caracterización detallada del yacimiento para definir el modelo estructural. Se involucra la evaluación de la incertidumbre asociada mediante clasificación jerárquica y selección de los modelos generados geoestadísticamente correspondientes a los cuantiles P₁₀, P₅₀ y P₉₀, con base en una variable indicadora del comportamiento del parámetro a evaluar. En la evaluación de la incertidumbre asociada al marco de referencia estratigráfico se utiliza como parámetro de jerarquización el porcentaje de yacimiento interconectado. La eficiencia volumétrica de barrido a un determinado tiempo, obtenida a partir del tiempo de vuelo de la simulación  streamline, se utiliza como la variable de clasificación jerárquica de los modelos petrofísicos.

MARCO TEÓRICO

Esta sección se ha distribuido en tres partes. En la primera, se presenta una descripción sobre el modelamiento geoestadístico que se utilizará para la definición del marco estratigráfico y petrofísico del yacimiento. La segunda parte, enfatiza en las generalidades y principios del modelo de simulación  streamline haciendo énfasis en el tiempo de vuelo y el cálculo de la eficiencia volumétrica de barrido. Finalmente, se hace una descripción de la técnica para ponderar modelos geoestadísticos.

MODELAMIENTO GEOESTADÍSTICO

La geoestadística y más específicamente el modelamiento de heterogeneidades del yacimiento, es considerado cada vez más por analistas e ingenieros de yacimientos, gracias a la habilidad y potencialidad de generar modelos de yacimiento más completos y precisos, junto con medidas de incertidumbre espacial. La geoestadística hace énfasis en la descripción y modelamiento de la variación espacial de las propiedades de yacimiento, además de la correlación espacial entre propiedades relacionadas tales como la porosidad, permeabilidad, contenido de arcilla, saturación de agua y la velocidad sísmica. La geoestadística suministra un marco de trabajo probabilístico y un conjunto de herramientas para análisis de datos que cuenta con una anticipada integración de la información. Los algoritmos de modelamiento estocástico permiten la generación de múltiples modelos de yacimiento, equiprobables y heterogéneos que hacen honor a los datos disponibles.

Para generar realizaciones geoestadísticas se emplea la técnica Simulación Gaussiana Secuencial (SGS). Este método permite simulaciones espaciales de secuencia de facies y el condicionamiento de estas a la información petrofísica perteneciente a los pozos en yacimientos de carácter clástico.

Simulación Gaussiana Secuencial (SGS)

Es un procedimiento estocástico y condicional debido a que los modelos generados hacen honor a los datos estáticos disponibles de los pozos. Detalles del método se pueden consultar en Deutsch y Journel (1998).

El primer paso de la SGS es la transformación de los datos conocidos en una distribución Gaussiana normal, utilizando una transformación no lineal.

El siguiente paso antes de la SGS es el modelamiento de los variogramas. Los variogramas son empleados para caracterizar los patrones de distribución espacial de la propiedad que se está modelando. El variograma mide el grado de similaridad entre dos muestras tomadas a diferentes distancias. Existen diferentes modelos de semivariogramas para encontrar la variación espacial, los cuales se pueden consultar en Deutsch y Journel (1998).

La fase final de la SGS consiste en realizar, en cada localización, un kriging simple en combinación con el modelo de semivariograma para determinar la distribución Gaussiana (Deutsch y Journel, 1998). El kriging es una herramienta geoestadística para determinar una propiedad en una localización no muestreada como una combinación lineal de las propiedades disponibles en las localizaciones vecinas.

Los métodos Gaussianos tienen el limitante de la dificultad inherente a explicar los contactos existentes entre zonas de alta con baja permeabilidad. En el artículo SPE 56515 "Characterizing Fluid Saturation Distribution Using Cross–Well Seismic and Well Data: A Geostatistical Study" (Idrobo et al., 1999) se trata el tema. Los campos Gaussianos presentan problemas pero no quiere decir ello que esta aproximación sea inválida.

La Figura 1 muestra el proceso de generación de una realización mediante el uso de SGS.

SIMULACIÓN STREAMLINE

Actualmente se cuenta con un gran compendio de autores que han presentado aplicaciones de la simulación streamline en diferentes campos, un excelente resumen sobre las características de la tecnología streamline se puede encontrar en el artículo "streamline simulation", de Marco Thiele (2001).

A diferencia de los modelos streamtube convencionales, los cuales son difíciles de aplicar a situaciones de campo que involucran múltiples pozos y condiciones de flujo en tres dimensiones (Thiele et al., 1996), la aproximación streamline se basa en un único algoritmo de tiempo de tránsito el cual usa como base de cálculo el tiempo de vuelo de una partícula a lo largo de la streamline. Datta Gupta y King (1995) hacen una descripción detallada del uso de streamline para el modelamiento de flujo en medios heterogéneos. El trabajo inicial para el trazado de las streamlines en tres dimensiones fue presentado por Pollock (1988).

Tiempo de vuelo

La variable fundamental en la simulación streamline es el tiempo de vuelo Τ_v que simplemente es el tiempo de viaje de una partícula a lo largo la línea de flujo hasta alcanzar un punto dado (Datta Gupta y King, 1995). El tiempo de vuelo matemáticamente puede definirse como:

Para flujo incompresible en un medio permeable no deformable, la velocidad es manejada por un campo de presión esta dado por la siguiente expresión:

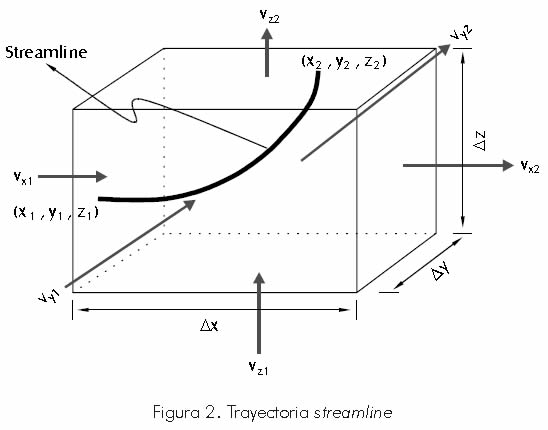
Donde Λ_i es la movilidad total, q es la fuente (pozo inyector) o el sumidero (pozo productor)  es un operador de divergencia Ñp es un operador gradiente de presión, Ñ Δ_ij es el delta de Kronecker que determina la posición del pozo en el nodo. El campo de presión se genera con un esquema de diferencias finitas. La de la ecuación 10 conduce a un sistema simétrico y bien definido de ecuaciones, el cual puede ser resuelto por métodos iterativos tales como el gradiente conjugado o la descomposición de Cholesky. Una vez se deriva la presión y por consiguiente el campo de velocidad, las trayectorias de las partículas y el tiempo de vuelo a lo largo de éstas se pueden calcular. Un esquema de las trayectorias de la partícula a lo largo de una streamline se presenta en la Figura 2.

La simplificación que se utiliza, es que en la representación del elemento finito del esquema diferencial de menor orden, cada velocidad varía linealmente a través de la celda y cada velocidad depende únicamente de su coordenada de posición. Una vez se deriva la presión y por consiguiente el campo de velocidad, las trayectorias de las partículas y el tiempo de vuelo a lo largo de éstas se pueden calcular integrando la siguiente expresión.

Donde v_x, v_y y v_z son las velocidades de las componentes en las direcciones x, y y z.Teniendo en cuenta que la línea de flujo debe salir a través de la cara cuyo tiempo de tránsito sea menor, entonces el delta de tiempo de tránsito de la línea de flujo en el bloque es dado por Datta Gupta y King (1995):

El tiempo de vuelo de la partícula (Τ), hasta un productor o hasta cualquier posición del dominio de flujo, puede obtenerse iniciando la trayectoria en el punto de interés y siguiendo hacia atrás la streamline en el tiempo, hasta llegar al pozo inyector. Todo lo anterior bajo la suposición de que la streamline no cambia significativamente con el tiempo. Este concepto, aplicado particularmente a procesos de inyección de agua, supone una buena aproximación, ya que la movilidad total por lo general es constante (Datta Gupta y King, 1995).

Eficiencia volumétrica de barrido

Desde otro punto de vista, el tiempo de vuelo refleja la propagación del frente de fluidos a varios tiempos, por lo tanto, existe una conexión directa entre el tiempo de vuelo y la eficiencia de barrido volumétrica. Idrobo et al. (2000) presentan la metodología para estimar dicha eficiencia de barrido en función del tiempo de vuelo.

Escribiendo la Ecuación 1 en forma diferencial:

Después de Bear (1973), la velocidad de campo para un medio 3D generalmente se puede expresar en términos de las bi–streamfunctions Ψ y Χ como:

Una streamline se define por la intersección de un valor constante para Ψ con un valor constante para Χ. En las aplicaciones en dos dimensiones, se usan las formas funcionales simplificadas Ψ = Ψ ( Χ , y) , Χ = z, lo que conlleva a expresiones más familiares v_x = ¶Ψ / ¶y , v_y = –¶Ψ / ¶x , donde Ψ se considera que sea la streamfunction.

Las técnicas streamline son basadas en una transformación de la coordenada del espacio físico a la coordenada del tiempo de vuelo, donde todas las streamlines son tratadas como líneas rectas de longitudes variables.

Idrobo et al. (2000) obtuvieron la siguiente expresión para calcular el volumen barrido

Donde, Θ es la función Heaviside y q (Ψ_i) es la tasa de flujo volumétrico asignada a la streamline Ψ_i . Finalmente la eficiencia volumétrica de barrido se puede calcular dividiendo por el volumen poroso total.

PONDERACIÓN DE MODELOS GEOESTADÍSTICOS

Cuantificar los impactos de tal incertidumbre sobre los pronósticos de comportamiento del yacimiento, haría necesario la simulación de flujo para un gran número de estas posibles descripciones del yacimiento. Sin embargo, las limitaciones computacionales evitan a menudo el uso de la totalidad de los modelos geoestadísticos en los pronósticos del yacimiento. Generalmente, se usan sólo algunas realizaciones seleccionadas para las simulaciones detalladas, esto para proporcionar una medida del rango de incertidumbre en el comportamiento del yacimiento.

Idrobo et al. (2000) propusieron un nuevo criterio de clasificación (ranking) para modelos geoestadísticos que utiliza la conectividad del tiempo de vuelo de la simulación streamline, la cual proporciona una estimación directa de la eficiencia de barrido areal o volumétrico.

El problema importante, como se anotó antes, son las limitaciones computacionales que impiden la ejecución de las simulaciones para cada una de las realizaciones geoestadísticas, que representan colectivamente la incertidumbre en la caracterización del yacimiento. Por consiguiente, para aplicaciones prácticas, es necesario poder seleccionar sólo unas cuantas realizaciones, que se usarán en las simulaciones detalladas, y luego extraer la información estadística (media y varianza) del comportamiento del yacimiento, mediante la ponderación apropiada de los resultados de estas simulaciones.

El método de Mishra y Kelley (2000) toma el planteamiento de Kaplan (1981) quien demuestra que una distribución continua, se puede reemplazar por una distribución discreta de tres valores con sus pesos ajustados de acuerdo con los momentos estadísticos (media y varianza) de la distribución continua. El primer paso es decidir que valores discretos de la variable indicadora deben seleccionarse para análisis futuros. A fin de capturar el rango completo de incertidumbre, se sugiere utilizar el valor de la mediana (percentil 50), junto con el percentil 10 (bajo) y el percentil 90 (alto). Los modelos geoestadísticos (realizaciones) correspondientes a estos valores discretos se convierten en los candidatos a llevar a cabo las simulaciones detalladas.

El segundo paso es decidir cómo ponderar (dar pesos estadísticos) los resultados de la simulación de cada una de las realizaciones seleccionadas. La metodología de ponderación presentada se basa en el hecho de que cualquier distribución continua, puede aproximarse mediante una distribución discreta, de tal forma que los momentos estadísticos de la distribución original se conserven, como se muestra en la Figura 3. Esto implica que si seleccionan los valores x₁, x₂ y x₃ como las representaciones discretas de la variable indicadora de comportamiento, x, entonces sus pesos respectivos, P₁, P₂ y P₃ deben satisfacer las siguientes limitaciones dadas por el algoritmo de ajuste de momentos estadísticos.

Donde E[ ] denota el valor esperado (expectation) estadístico o media y V[ ] denota la varianza. Es de anotar que x es cualquier variable indicadora de comportamiento del yacimiento, y los valores x₁, x₂ y x₃ corresponden a las realizaciones R₁, R₂ y R₃, respectivamente. De la distribución continua de x, se conoce E[x] y V[x]; así, una vez las cantidades discretas x₁, x₂ y x₃ son seleccionadas, se calculan los pesos P₁, P₂ y P₃ usando las Ecuaciones 23 y 24. El algoritmo de ajuste contempla una limitación adicional, la cual requiere que los pesos de las distribuciones discretas sumen la unidad.

Las realizaciones seleccionadas en este proceso (R₁, R₂ y R₃) se usan como datos de entrada en las simulaciones de flujo multifásico para calcular las variables de interés del comportamiento real (corte de agua, recobro de aceite). La variable de interés se denota como Ξ entonces, la incertidumbre de Ξ en los pronósticos, puede caracterizarse así:

Donde M[ ] denota la media y SD[ ] la desviación normal.

METODOLOGÍA PROPUESTA

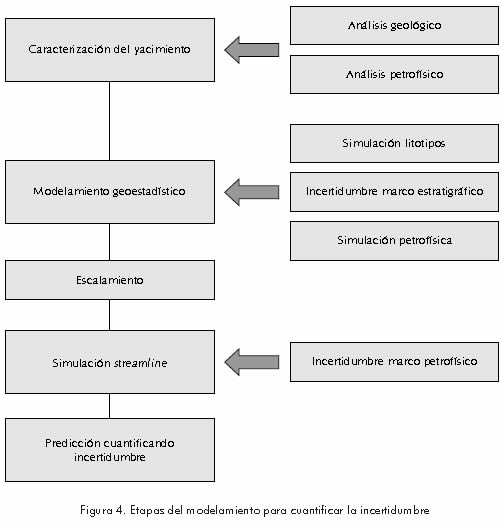
A continuación se relaciona una descripción de la metodología, de las diferentes etapas de desarrollo del proyecto. Con esta metodología se pretende optimizar la evaluación de la incertidumbre asociada a los pronósticos de producción de un yacimiento altamente heterogéneo sometido a inyección de agua. La Figura 4 presenta, de manera secuencial, las etapas de un modelamiento de esta naturaleza.

Caracterización del yacimiento

Entender la distribución espacial de las diferentes propiedades del yacimiento es esencial para alcanzar la mejor caracterización del yacimiento. Es necesario contar con un buen número de datos de corazones, registros eléctricos, pruebas de presión y datos de producción provenientes de un número adecuado de ubicaciones representativas del área en estudio. Además, los diferentes tipos de datos suministran variaciones en la información del yacimiento debido a sus diferencias en resolución y volumen de investigación.

Caracterización geológica

Esta etapa consiste en el estudio de la zona de interés a través de técnicas geológicas y geofísicas, entre las que se incluyen interpretaciones sedimentológicas, análisis de secuencias estratigráficas, geología estructural y sísmica entre otras. Estas interpretaciones son realizadas principalmente a partir de información de los registros eléctricos y datos de corazones.

Se considera que la definición geológica es fundamental para un yacimiento de naturaleza fluvial, ya que mientras exista un alto grado de conocimiento de sus características, entonces se dispondrá de un modelo estático aceptable y por ende el grado de incertidumbre asociada será menor.

Caracterización petrofísica

Se realiza por medio de la generación del modelo matemático para cada una de las variables petrofísicas del yacimiento entre las que se cuentan porosidad efectiva, permeabilidad efectiva, saturación de agua y contenido de arcilla. Este modelo se desarrolla para cada uno de los pozos del área en estudio a partir de información de núcleos, registros de pozos y pruebas de presión. Es de anotar que para el desarrollo particular de este proyecto, el modelo petrofísico de permeabilidad involucra la variable categórica asociada a la estratigrafía del yacimiento.

Modelamiento geoestadístico

La Figura 5 resume las principales etapas del proceso.

Para el desarrollo de esta etapa del proceso se consideran los siguientes aspectos:

– Después de realizar un análisis geológico a los datos de entrada, el yacimiento es definido como una(s) litounidad(es), teniendo en cuenta los modelos conceptuales proporcionados por la estratigrafía de secuencias. La unidad se define teniendo en cuenta la homogeneidad del ambiente geológico de depositación y los marcadores cronoestratigráficos que delimitan los miembros estratigráficos.

– Se define la geometría del modelo de yacimiento a partir de la caracterización geológica: marcos estructural y de referencia estratigráfica, mediante la construcción de una malla de referencia. Posteriormente, se efectúa la generación del modelo estático del yacimiento a partir de la caracterización petrofísica a nivel de pozo. El objetivo de esta etapa es caracterizar la geometría externa de la unidad y la distribución espacial interna de los cuerpos sedimentarios junto con sus propiedades petrofísicas.

– Utilizando la técnica geoestadística de Simulación Gaussiana Secuencial se efectúan las simulaciones a los litotipos definidos, lo cual proporciona una representación de la geología del yacimiento y de las distribuciones de facies en un enmallado de alta resolución. Ello es denominado marco de referencia estratigráfico.

– Como se desea cuantificar la incertidumbre asociada al marco estratigráfico, se procede a seleccionar un único modelo de yacimiento mediante técnicas de jerarquización. Una vez se cuenta con un número considerable de realizaciones estratigráficas y considerando el porcentaje de yacimiento interconectado como parámetro de jerarquización, se selecciona la simulación geoestadística correspondiente al percentil 50, como el más probable modelo base para el modelamiento petrofísico.

– Considerando un único modelo estratigráfico se generan las diferentes e equiprobables descripciones de las propiedades petrofísicas porosidad y permeabilidad, empleando nuevamente la técnica de SGS. Se obtiene como producto un modelo de yacimiento de alta resolución con descripciones de propiedades estratigráficas y petrofísicas.

Para el modelamiento geoestadístico se utilizó el Software HERESIM del IFP.

Escalamiento

Los modelos de alta resolución contemplados para la etapa del modelamiento geoestadístico son por lo general de varios millones de celdas, los cuales implican ciertas dificultades en lo que se refiere al manejo computacional de una simulación de flujo de fluidos. Por lo anterior, es conveniente realizar un escalamiento (upscaling), al modelo de yacimiento de alta resolución, de sus propiedades estratigráficas y petrofísicas. El propósito de este proceso es obtener un modelo cuyas dimensiones sean manejables en los paquetes de simulación comercial disponibles en el mercado. El escalamiento proporciona un puente entre las dos escalas mencionadas. Partiendo de una descripción de yacimiento de alta resolución y con un enmallado de simulación definido, los algoritmos de escalamiento asignan valores adecuados de porosidad, permeabilidad y otras variables de flujo a las celdas del enmallado de simulación. En este proyecto se usó como técnica de escalamiento la propuesta por Idrobo et al. (2003), no siendo uno de los alcances del presente trabajo discutir esta tarea.

Simulación streamline

Para la etapa de modelamiento del flujo de fluidos se considera la simulación streamline, la cual ha probado ser altamente eficiente para el modelamiento de yacimientos con grandes heterogeneidades, en los cuales el mecanismo de flujo dominante es consecuencia de las fuerzas viscosas, como es el caso de sistemas ligeramente compresibles sometidos a inyección de agua.

La simulación streamline es básicamente un procedimiento IMPES que utiliza los mismos principios de la simulación en diferencias finitas pero resuelve el problema de saturación en el espacio tiempo de vuelo en lugar de utilizar la malla cartesiana.

La simulación streamline resuelve un problema tridimensional mediante el desacoplamiento en una serie de problemas unidimensionales y usando la técnica numérica IMPES. La estrategia consiste en resolver la ecuación de presión implícitamente para calcular el conjunto de streamlines que representan el flujo en el yacimiento. Cada streamline representa una tasa volumétrica y actúa como un enmallado unidimensional corriendo perpendicular al contorno de presión del yacimiento, a diferencia de los simuladores convencionales en los cuales el fluido es confinado a una celda y su movimiento es en dirección ortogonal a la cara de la celda. La Figura 6 muestra esquemáticamente el proceso de simulación streamline.

Idrobo et al. (2000) probaron la conexión directa entre el tiempo de vuelo y la eficiencia de barrido volumétrica. Es por lo anterior que la eficiencia de barrido volumétrico, obtenida a partir del tiempo de vuelo de la simulación streamline se utiliza como variable indicadora del comportamiento dinámico, para la jerarquización de los modelos petrofísicos.

Cuantificación de la incertidumbre

Con base en la variable eficiencia de barrido como parámetro de jerarquización (Idrobo et al., 2000) y el método probabilístico híbrido (Mishra et al., 2000) se seleccionan las realizaciones petrofísicas correspondientes a los percentiles estadísticos 10, 50 y 90. Estas realizaciones son consideradas para las corridas de la simulación streamline. Posteriormente, se realiza una comparación de los resultados obtenidos entre las simulaciones obtenidas con las tres realizaciones seleccionadas y las simulaciones de todas las realizaciones petrofísicas.

La metodología propuesta suministra un marco de trabajo conveniente desde el punto de vista computacional, al calcular la media y la varianza de las variables de interés del comportamiento del yacimiento, para cuantificar la incertidumbre, considerando sólo unos cuantos modelos geoestadísticos (sus pesos estadísticos se calculan con base a una variable indicadora del comportamiento).

Los resultados obtenidos muestran una excelente concordancia, lo cual da soporte y validez a la metodología propuesta.

CASO DE CAMPO: AREA 07, ZONA C, CAMPO LA CIRA–INFANTAS, COLOMBIA

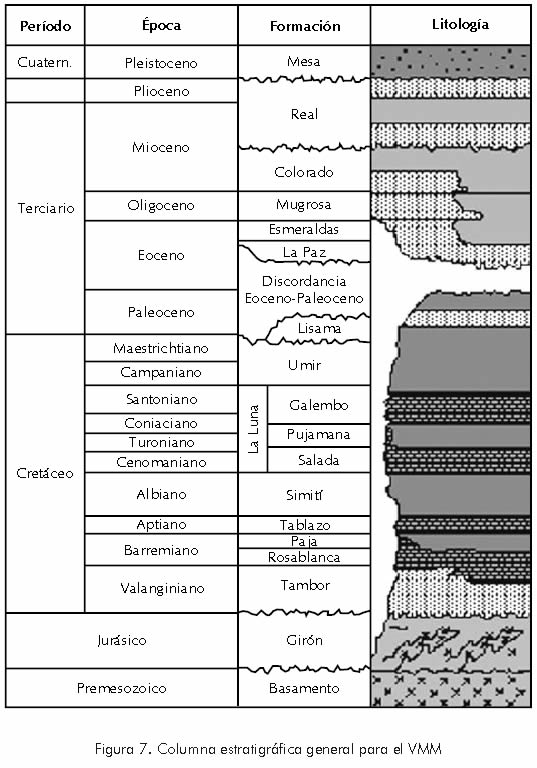
El Campo La Cira–Infantas es un anticlinal alongado de 9 km de longitud por 6 km de ancho, el eje principal se encuentra en dirección Norte – Sur. El Campo La Cira produce de tres zonas "A", "B" y "C" (ver columna estratigráfica – Figura 7). La zona "C" es un yacimiento de arenas fluviales de permeabilidad baja a moderada (50 – 200 md). Esta zona contiene aproximadamente el 80% del Original Oil in place (OOIP) del Campo La Cira. Las zonas "C" y "B" producen de la formación Mugrosa correspondiente a la edad Eoceno – Oligoceno y la zona "A" produce de la formación Colorado de edad Oligoceno–Mioceno.

En la actualidad se han perforado en el área de La Cira–Infantas 1716 pozos, de los cuales hay aproximadamente 580 pozos productores activos, 81 pozos inyectores de agua activos, 592 pozos productores inactivos, 106 pozos inyectores inactivos y 357 pozos abandonados.

El OOIP del campo La Cira–Infantas es de 3594 MMbls la producción promedio de aceite actual es de 5700 BOPD (Diciembre de 2002), con una producción de aceite acumulada de 798,15 MMbls y una inyección acumulada de 957,4 MMbls (Diciembre de 2001).

En el área 07, la zona C inició su explotación en 1933 con el pozo LC–745 con 1132 bapd. El principal desarrollo de esta área se llevó a cabo entre los años 1933 y 1941 cuando se perforaron 124 pozos, de los cuales 99 penetraron la zona C. La inyección se inició en 1971 con modelos regulares de seis y siete puntos, modificados posteriormente a modelos de cuatro a siete puntos, por problemas mecánicos de los pozos.

Para realizar el modelo estratigráfico y el modelo petrofísico se seleccionaron 65 pozos, los cuales se pueden observar en la Figura 8. Algunos de los criterios que se tuvieron a la hora de realizar esta selección fueron:

– Pozos corazonados.

– Pozos perforados más recientes.

– Que tuvieran una buena distribución areal (cobertura total del área).

– Que estuviera representada la geomorfología de las unidades definidas.

Modelo de simulación

Un total de 12 pozos, tres pozos productores y nueve pozos inyectores, se utilizan en el modelo. La Figura 8 presenta una vista areal de la ubicación del modelo usado. Las dimensiones de la malla de simulación son: 15 960 celdas (19 x 28 x 30), el tamaño de cada bloque es de 55m x 52m y con tamaño variable en z. El simulador utilizado es el S3D de la Texas A&M University.

El flujo fue asumido incompresible puesto que se modeló a partir del comienzo de la inyección de agua. El simulador recalcula las streamlines cada vez que se presenta un nuevo infill (evento) y se asume que en el modelo, al estar el yacimiento por encima del punto de burbuja (después del primer evento), no se presentan problemas de compresibilidad por gas. Se usó un simulador de diferencias finitas sólo para calcular la distribución espacial de saturación de agua al inicio de la inyección de agua.

Parámetros importantes para el modelamiento del flujo de fluidos tales como: permeabilidades verticales, permeabilidades relativas, modelo de saturationes, relaciones net–to–gross, contactos de los fluidos y datos PVT; son mostrados en la tesis de maestría del autor principal del presente artículo (Mantilla, 2003).

RESULTADOS

Modelo estratigráfico

Se generaron 51 modelos litológicos del yacimiento, utilizando geoestadística, para garantizar que se está asociando la incertidumbre al marco de referen–
cia estratigráfico utilizando la técnica Indicator Gaussian Simulation.

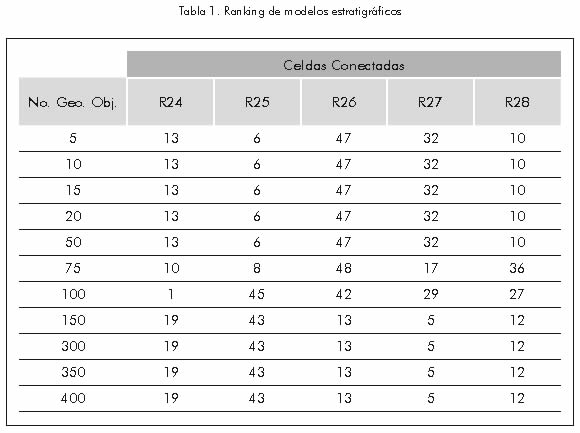
Se utilizó como parámetro de jerarquización el porcentaje de yacimiento interconectado (Deutsch, 1998) y se selecciona la realización correspondiente a la ubicación del percentil 50, que corresponde a un escenario promedio, esto para no considerar los escenarios muy optimista ni muy pesimista (percentiles 10 y 90 respectivamente). Después de realizar un estudio de sensibilidad para diferentes cantidades de geo–objetos conectados, se deduce que la realización número 47 ocupa el percentil 50 (para un número de hasta 50 geo–objetos) como se puede observar en la Tabla 1.

Modelo petrofísico

Aplicando SGS sobre el modelo estratigráfico previamente establecido se generaron 51 realizaciones petrofísicas (distribución espacial de permeabilidad, porosidad y Vshale). Estas simulaciones se jerarquizan usando la eficiencia volumétrica de Barrido, calculada a partir de la conectividad del tiempo de vuelo como lo describen Idrobo et al. (2000). Los valores de la eficiencia volumétrica para cada simulación se presentan en la Tabla 2.

Con los valores de la eficiencia volumétrica de barrido obtenidos para cada una de las simulaciones, se procede a construir la curva de función de distribución acumulada, Cumulative Distribution Function (CDF), con el objetivo de clasificar las realizaciones geoestadísticas. La CDF obtenida se muestra en la Figura 9 donde se puede observar el ranking de la variable de interés para cada una de las simulaciones corridas.

Ponderación de las realizaciones geoestadísticas

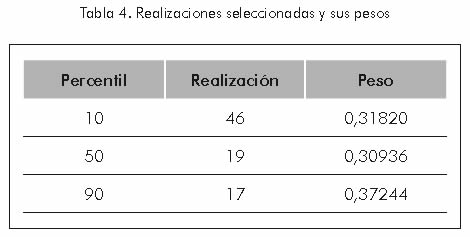
Para el caso de estudio se toma la distribución continua, obtenida al jerarquizar las realizaciones geoestadísticas, y se seleccionan los cuantiles P₁₀, P₅₀ y P₉₀ con el fin de capturar el rango completo de incertidumbre de acuerdo con lo que sugieren Mishra y Kelley (2000). Si se observa nuevamente la Figura 9, se puede ver que los cuantiles P₁₀, P₅₀ y P₉₀ corresponden a las realizaciones 5, 19 y 46 respectivamente.

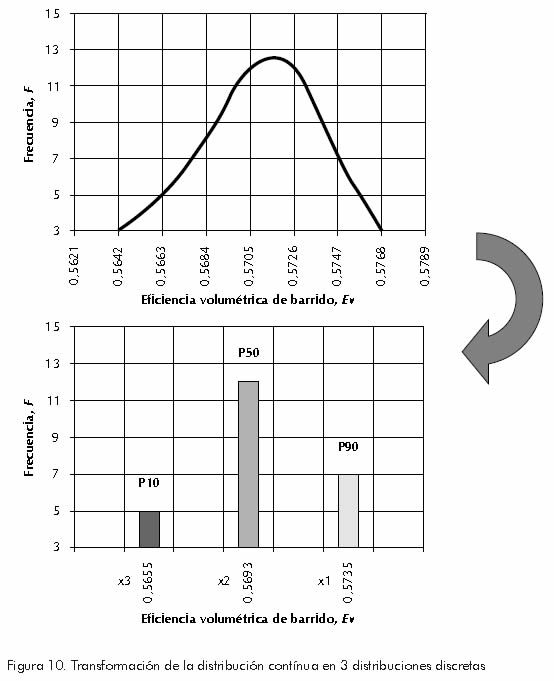
Al analizar la Figura 10, que representa el proceso de transformación de una función continua en una función discreta, se puede decir que si se escogen los valores x₁, x₂ y x₃ como representaciones discretas de la variable de medida del desempeño, x, (Ev) entonces los respectivos pesos deben satisfacer las ecuaciones 8 y 9 que son parte del algoritmo de ajuste de los momentos estadísticos. E[x] y V[x] son el promedio y la varianza y se obtienen aplicando estadística descriptiva a la distribución continua de Ev. Los valores de estos parámetros se presentan en la Tabla 3. Finalmente aplicando las ecuaciones 8, 9 y 10, se determina el valor de los pesos para cada una de las realizaciones. Los resultados se presentan en la Tabla 4.

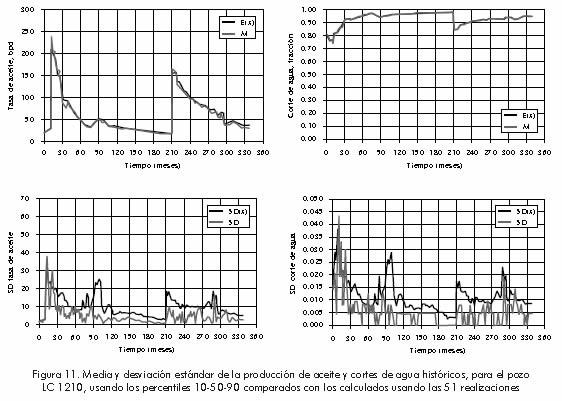
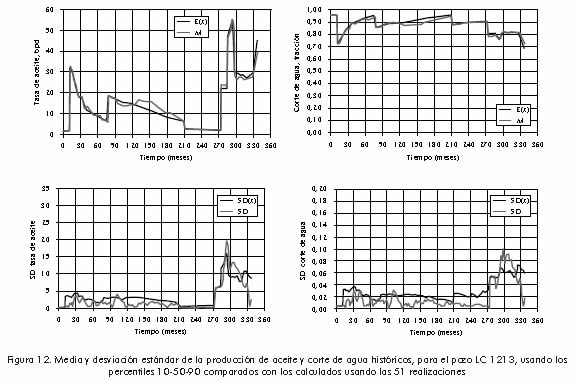
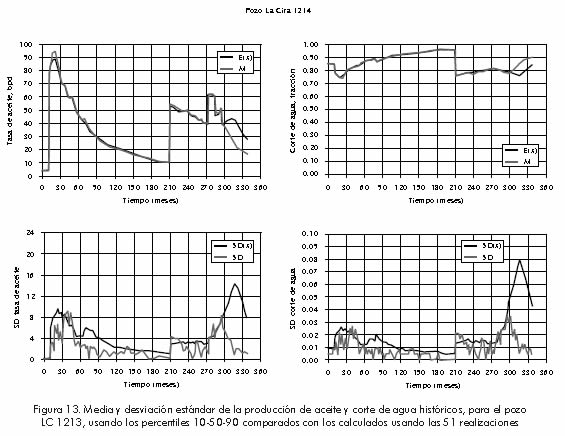
Se corrieron simulaciones para las tres realizaciones seleccionadas, y sus resultados fueron combinados usando los pesos obtenidos anteriormente con el objetivo de determinar la media y la desviación estándar del corte de agua histórico aplicando las ecuaciones 11 y 12. Finalmente en las Figuras 11, 12 y 13 se presentan el corte de agua histórico y la tasa de producción de aceite los cuales ya tienen asociada la incertidumbre tanto del marco estratigráfico como del marco petrofísico.

Validación del esquema de ponderación propuesto

Con el fin de evaluar la exactitud del esquema de asignación de pesos propuesto, se llevaron a cabo simulaciones para todas las 51 realizaciones. Para cada etapa de tiempo se calculó la media y la desviación estándar, tanto del corte de agua como de la tasa de producción de aceite, de las 51 simulaciones. La comparación entre los resultados del método propuesto y aquellos obtenidos de todas las simulaciones muestran una buena correspondencia. Los resultados comparativos para cada uno de los pozos productores del modelo se muestran en las Figuras 11–13. Estos corresponden a los cuantiles P₁₀, P₅₀ y P₉₀ involucrados en la media del corte de agua histórico de todas las simulaciones, E(x) y la media calculada del corte de agua histórico, M, de las tres simulaciones, con la desviación estándar SD(x) (de todas las simulaciones) y SD (de las tres simulaciones) usadas como una medida del error en los datos.

La validez de la metodología de ponderación se probó seleccionando los cuantiles P₁₀, P₅₀ y P₉₀ para el proceso de simulación, estos cuantiles fueron seleccionados de la CDF basada en la eficiencia volumétrica de barrido.

En general el desempeño de la metodología propuesta es satisfactorio en la predicción del corte de agua histórico promedio con únicamente tres simulaciones. Si se observa la predicción de la desviación estándar para cada uno de los pozos del modelo se nota una diferencia entre las dos curvas, pero ésta tiene que ser vista bajo el contexto de la relativa baja magnitud de la escala de la desviación estándar comparada con la media.

La etapa final del análisis de incertidumbre es hacer un pronóstico del corte de agua y de la tasa de producción para el área seleccionada.

Pronóstico de producción y corte de agua asociando la incertidumbre

Finalmente probada la validez de la metodología de ponderación se procede a realizar el pronóstico de corte de agua y tasa de producción para el área de estudio utilizando las tres realizaciones seleccionadas (P₁₀, P₅₀ y P₉₀).

Los datos históricos del área de estudio están disponibles hasta enero de 1999. La predicción se hace para 5 años, es decir hasta enero de 2004.

Para obtener los pronósticos de tasa de producción y corte de agua se hizo simulación a cada uno de las realizaciones seleccionadas y luego sus resultados fueron combinados con los pesos calculados anteriormente. Los resultados obtenidos se muestran en las Figuras 14 a 16. Al combinar los percentiles P10, P50 y P90, se garantiza que la incertidumbre, asociada al marco estratigráfico y al marco petrofísico, se tiene en cuenta dentro de los pronósticos realizados.

Al comparar los resultados obtenidos por el simulador con los datos históricos se puede decir que el pozo La Cira 1210 es el que mejor ajusta tanto en la tasa de producción como en el corte de agua. Esto se explica debido a que este pozo está situado en la parte baja de la estructura, lo que implica que la cantidad de gas libre al inicio de la inyección era menor que la de los otros dos pozos y como se había comentado anteriormente la versión del simulador utilizada para este estudio no maneja fluidos compresibles.

El pozo de menor ajuste es La Cira 1214 donde se observa que el corte de agua del simulador aumenta rápidamente comparado con el corte de agua histórico. Puede decirse que este es el pozo estructuralmente más alto y por lo tanto el que tiene mayor efecto por presencia de gas.

En términos generales la capacidad predictiva del modelo es buena debido a que la producción real de los pozos productores ajusta con la producción calculada por el simulador.

CONCLUSIONES

• La integración de diferentes metodologías y herramientas ha permitido presentar un procedimiento robusto para llevar a cabo la predicción de parámetros de producción, en un yacimiento heterogéneo sometido a inyección de agua, los cuales son la base para hacer un análisis económico de riesgo.
• La cuantificación de la incertidumbre con esta metodología es doble. Se examinó no sólo el marco de referencia estratigráfico usando la conectividad de las facies productoras como variable de jerarquización, sino también el modelo petrofísico usando la Eficiencia Volumétrica de Barrido basada en el concepto de tiempo de vuelo, como variable indicadora.
• Para alcanzar el objetivo de obtener un modelo de simulación sólido y consistente, se combinaron los estudios sedimentológicos, modelos conceptuales estratigráficos de secuencias y técnicas de modelamiento geoestadístico para el cálculo de las distribuciones petrofísicas 3D, tanto de alta como de baja resolución del yacimiento. La metodología aplicada permitió la elaboración de un modelo de simulación con una base muy sólida en la parte petrofísica, geológica, estratigráfica y estructural.
• Al analizar los pronósticos de producción y corte de agua se puede ver que los pozos 1213 y 1214 presentan una marcada desviación del comportamiento histórico debido probablemente a la presencia de gas en el yacimiento al inicio del proceso de recuperación secundaria. Es importante resaltar que una de las principales limitaciones de la simulación streamline es la de modelar procesos compresibles.

BIBLIOGRAFÍA

Bear, J., 1973. "Dynamics of fluid in porous media". Dover Publications, New York.         [ Links ]

Craig, F. F., 1971. "The reservoir engineering aspects of waterflooding" . SPE Monograph 3, Richardson, TX.         [ Links ]

Datta-Gupta, A. and King, M. J., 1995. "A semianalytic approach to tracer flow modeling in heterogeneous permeable media". Advances in Water Resources, 18 (1): 9-24.         [ Links ]

Deutsch, C. V. and Journel, A. G., 1998. "GSLIB: Geostatistical Software Library and User’s Guide". Second edition, Oxford University Press, New York.         [ Links ]

Deutsch, C. V., 1998. "Fortran programs for calculating connectivity of three-dimensional numerical models and for ranking multiple realizations". Computers & Geosciences, 24 (1): 69.         [ Links ]

Idrobo, E. A., 1999. "Characterization and ranking of reservoir models using geostatistics and streamline simulation". PhD Dissertation, Texas AYM University, 90 pp.         [ Links ]

Idrobo, E. A., Mallah, A. H., Datta-Gupta, A. and Parra, J. O., 1999. "Characterizing fluid saturation distribution using cross-well seismic and well data: a geostatistical study". Paper SPE 56515 presented at the 1999 SPE Annual Technical Conference and Exhibition, Houston, Texas.         [ Links ]

Idrobo, E. A., Choudhary, M. K. and Datta-Gupta, A., 2000. "Swept volume calculations and ranking of geostatistical reservoir models using streamline simulation". Paper SPE 62557 presented at the 2000 SPE/AAPG Western Regional Meeting, Long Beach, California.         [ Links ]

Idrobo, E. A., Jimenez, E. A., Ospino, A. A. and Arroyo, E. A., 2003. "A new tool to uphold spatial reservoir heterogeneity for upscaled models". Paper SPE 81041 presented at the SPE Latin American and Caribbean Petroleum Engineering Conference, Port-of-Spain, Trinidad, West Indies.         [ Links ]

Kaplan, S., 1981. "On the method of discrete probability distributions" . Risk Analysis, 1: 189.         [ Links ]

Mantilla, J., 2003. "Cuantificación de la incertidumbre asociada en la predicción del comportamiento de producción de un yacimiento altamente heterogéneo sometido a inyección de agua: campo La Cira". Tesis maestría Escuela de Petróleos, Universidad Industrial de Santander, 157 pp.         [ Links ]

Mishra, S. and Kelley, V. A., 2000. "A hybrid probabilistic approach for health risk assessments". Paper W18.01 presented at the 2000 Society for Risk Analysis Annual Meeting, Atlanta, Georgia.         [ Links ]

Pollock, D. W., 1988. "Semi analytical computation of path lines for finite-difference models".Ground Water, 743-750.         [ Links ]

Schoeppel, R. J., 1968. "Waterflood prediction methods" . Oil and Gas J., 66, Jan. 22, 72-75; Feb. 19, 98-106; March 18, 91-93; April 8, 80-86; May 6, 111-114; June 17, 100-105; July 8, 71-79.         [ Links ]

Texas AYM University, 2000. "S3D Streamline Simulator: User Manual, Ver.1.1"         [ Links ].

Thiele, M. R., Batycky, R. P., Blunt, M. J., and Orr, F. M., 1996. "Simulating flow in heterogeneous media using streamtubes and streamlines". SPE Reservoir Engineering, 10 (1): 5-12.         [ Links ]

Thiele, M. R. and Edwards, M. G., 2001. "Physically based higher-order godunov schemes for compositional simulation". Paper SPE 66403 in proceedings of the 2001 SPE Reservoir Simulation Symposium, Houston, TX.         [ Links ]

Thiele, M. R. y Batycky, R. P., 2001. "Discussion of SPE65604- streamline simulation: a technology update", J. of Petro. Technol., 53 (5): 26-27.         [ Links ]

Thiele, M. R., 2001. "Streamline simulation". 6th International Forum on Reservoir Simulation, September 3rd-7th, Schloss Fuschl, Austria.         [ Links ]