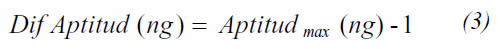Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.2 no.5 Bucaramanga Jan./Dec. 2004
CARACTERIZACIÓN DINÁMICA DE YACIMIENTOS ESTRATIGRÁFICAMENTE COMPLEJOS USANDO ALGORITMOS GENÉTICOS
Santiago González*1 y Eduardo A. Idrobo*2
1Ecopetrol – Gerencia Centro Oriente, El Centro, B/bermeja, Santander, Colombia
2Ecopetrol – Instituto Colombiano del Petróleo, A.A. 4185 Bucaramanga, Santander, Colombia
e–mail: sagonzal@ecopetrol.com.co e–mail: aidrobo@ecopetrol.com.co
(Recibido Junio 11 de 2003; Aceptado Septiembre 20 de 2004)
* A quien debe ser enviada la correspondencia
RESUMEN
En este trabajo se presenta la aplicación a un caso real de una metodología novedosa para la caracterización de yacimientos altamente heterogéneos mediante la integración de la información dinámica del yacimiento al modelo estático actualizado. La metodología fue desarrollada por el Dr. Carlos Romero, quien la aplicó a un yacimiento sintético.
El proceso de caracterización de yacimientos tiene como objetivo construir un modelo del yacimiento, lo mas realista posible, mediante la incorporación de toda la información disponible. El enfoque clásico consiste en elaborar un modelo que se fundamenta en la información estática del yacimiento, teniendo como etapa final del proceso la validación del modelo con la información dinámica disponible. Es importante aclarar que el término validación implica un proceso por naturaleza puntual, generalmente asociado a asegurar solamente la coherencia requerida entre zonas productoras y propiedades petrofísicas.
El objetivo de la metodología propuesta es mejorar la capacidad de predicción del modelo del yacimiento mediante la integración a priori de los parámetros intrínsecos a la dinamicidad de los fluidos del yacimiento mediante un proceso de inversión dinámica de datos a través de un procedimiento de optimización basado en computación evolutiva.
La metodología propuesta parte de la construcción del modelo estático del yacimiento de alta resolución, el cual es escalado mediante técnicas híbridas buscando preservar la heterogeneidad del yacimiento. Posteriormente, usando como marco de referencia un simulador analítico, el modelo escalado es metódicamente modificado mediante un proceso de optimización que usa algoritmos genéticos y como información condicional los datos de producción.
El Producto final de este proceso es un modelo que respeta las condiciones estáticas y dinámicas del yacimiento con capacidad de minimizar el impacto económico que genera el ajuste histórico de producción en las tareas de simulación. Este modelo final, entonces, presenta unas propiedades petrofísicas (porosidad, permeabilidad y saturación de agua) modificadas para lograr un mejor ajuste de la historia de producción simulada con la real (History Matching). Adicional a lo anterior, el proceso involucra una liguera modificación de las permeabilidades relativas, las cuales se han cambiado buscando calibrar estas propiedades que igualmente presentan un grado alto de incertidumbre.
Palabras claves: caracterización de yacimientos, modelamiento geoestadístico, simulación streamline, algoritmos genéticos, optimización global, ajuste histórico automático.
ABSTRACT
A novel methodology is presented in this paper for the characterization of highly heterogeneous oilfields by integration of the oilfields dynamic information to the static updated model.
The objective of the oilfield's characterization process is to build an oilfield model, as realistic as possible, through the incorporation of all the available information. The classical approach consists in producing a model based in the oilfield's static information, having as the process final stage the validation model with the dynamic information available. It is important to clarify that the term validation implies a punctual process by nature, generally intended to secure the required coherence between productive zones and petrophysical properties.
The objective of the proposed methodology is to enhance the prediction capacity of the oilfield's model by previously integrating, parameters inherent to the oilfield's fluid dynamics by a process of dynamic data inversion through an optimization procedure based on evolutionary computation.
The proposed methodology relies on the construction of the oilfield's high resolution static model, escalated by means of hybrid techniques while aiming to preserve the oilfield's heterogeneity. Afterwards, using an analytic simulator as reference, the scaled model is methodically modified by means of an optimization process that uses genetic algorithms and production data as conditional information.
The process's final product is a model that observes the static and dynamic conditions of the oilfield with the capacity to minimize the economic impact that generates production historical adjustments to the simulation tasks. This final model features some petrophysical properties (porosity, permeability and water saturation), as modified to achieve a better adjustment of the simulated production's history versus the real one (History Matching). Additionally, the process involves a slight modification of relative permeabilities, which have been changed to allow calibration of these properties that also feature a high degree of uncertainty.
Keywords: reservoir characterization, geostatistical modeling, streamline simulation, genetic algorithms, global optimization, automatic history matching
INTRODUCCIÓN
El proceso de caracterización de yacimientos tiene como objetivo construir un modelo del yacimiento, lo más realista posible, mediante la incorporación de toda la información disponible. El enfoque clásico consiste en elaborar un modelo que se fundamenta en la información estática del yacimiento, teniendo como etapa final del proceso la validación del modelo con la información dinámica disponible.
La metodología aplicada fue, inicialmente desarrollada por el Dr. Carlos Romero (Romero, 2000) como tesis de doctorado; sin embargo, aquí fue ajustada mediante la incorporación de las siguientes modificaciones:
- Se trabajó en la definición de la distribución volumétrica de las propiedades del yacimiento mediante técnicas geoestadísticas detalladas, utilizando definiciones litológicas (estratigrafía de detalle).
- Se mejoró la velocidad del método utilizando el concepto de simulación streamline.
- Se redefinieron:
- – los cromosomas (variables) a optimizar (hubo una disminución, ya no se contemplaron las transmisibilidades de las fallas ni factor Skin en los pozos).
- – la Función Objetivo.
- – Calculo de la Aptitud.
- – Estrategias de Selección.
- – La forma como se aplican los operadores genéticos.
- – El procedimiento de actualización de la población.
- Todo el proceso se programó en plataforma PC que utiliza como sistema operativo Microsoft Windows©. Se debe resaltar que el programa que permite la ejecución de la metodología se realizó exclusivamente para esta investigación (INVERDIMANICA©), el cual se encarga de controlar (manejar) todas las aplicaciones adicionales, necesarias para automatizar el proceso de ajuste histórico. Estas aplicaciones son: Microsoft Excel, S3D© (Simulador de Streamline) y SGSIM© (Simulador de Geoestadística). Para comprobar los resultados obtenidos se utilizó el streamline (Simulador Numérico).
El objetivo de la metodología propuesta es mejorar la capacidad de predicción del modelo del yacimiento mediante la integración a priori de los parámetros intrínsecos a la dinamicidad de los fluidos del yacimiento usando un proceso de inversión dinámica de datos a través de un procedimiento de optimización basado en computación evolutiva. Esta tesis se enfoca en la aplicación de los Algoritmos Genéticos (AGs) a la caracterización de yacimientos de hidrocarburos.
La metodología utiliza un AG especialmente diseñado para buscar descripciones del yacimiento que hacen honor tanto a los datos de los pozos como a sus historias de producción, siempre y cuando se tengan los modelos geológico, estratigráfico y petrofísico previamente definidos. Este AG se combina con el modelamiento geoestadístico para generar múltiples descripciones del yacimiento. El resultado es un conjunto de posibles soluciones (correspondientes a diferentes realizaciones del modelo del yacimiento), a partir de las cuales se puede seleccionar la más apta para análisis posteriores.
Los yacimientos de hidrocarburos están compuestos, por lo general, de rocas sedimentarias heterogéneas que contienen dependiendo del caso: aceite, gas y agua. Para conocer cómo se comportan estos fluidos en el yacimiento, se utilizan los simuladores. Para su aplicación, el yacimiento debe estar dividido en celdas discretas que conforman una gran malla, por lo general, las propiedades en estas celdas son desconocidas. Posteriormente, se debe llevar a cabo un proceso de calibración en el cual los resultados son comparados con la información histórica del yacimiento. Esta calibración la hace el ingeniero mediante la variación de algunas de las propiedades de las celdas hasta obtener un ajuste adecuado.
Esta metodología automatiza este proceso, minimizando el impacto económico que genera el ajuste histórico de la producción en las tareas de simulación y el modelo resultante incorpora toda la información disponible (estática y dinámica), por lo tanto será el más realista posible. Esta automatización se logra al considerar el ajuste histórico como un proceso de optimización multivariable (el cual puede tener varios óptimos). Teniendo en cuenta esta última reflexión, se impone como requerimiento un método de optimización global, dentro de los cuales, los AGs han demostrado una alta eficiencia en la solución de este tipo de problemas.
Los AGs usan ideas de la teoría de evolución de las especies de Darwing, donde sólo los organismos (individuos) más fuertes sobreviven adaptándose a las diferentes condiciones que el medio les imponga (más aptos). Estos organismos tienen una información genética que los hace únicos y, por lo tanto, cambios pequeños en estos códigos los hacen más fuertes o por el contrario más vulnerables.
Los resultados obtenidos superan las expectativas que se tenían en relación con esta metodología, la cual, sólo había sido probada en un yacimiento sintético, proveyendo un procedimiento que se puede aplicar aún cuando se tenga una alta incertidumbre en cuanto a parámetros tales como: propiedades petrofísicas determinadas con registros "viejos", datos de producción e inyección de agua. Otra ventaja que se tiene es que se puede utilizar en yacimientos tanto en producción primaria como en recobro secundario; sin embargo, los tiempos de cómputo serán mayores para los casos de campos en producción primaria.
Todo el programa corre en plataforma PC ambiente Microsoft Windows©, lo cual le permite sacar provecho de: uso en cualquier equipo, utilización de la última tecnología en PC para acortar los tiempos de cómputo y menores costos en relación con los equipos en plataforma UNIX.
DESCRIPCIÓN PROCESO CARACTERIZACIÓN
A continuación se hace una presentación y descripción general de la secuencia que realiza el programa INVERDINAMICA ©. El software fue desarrollado, en particular, para automatizar el proceso de ajuste histórico de un modelo de yacimiento en plataforma PC.
Cada corrida involucra: cargar los datos básicos del yacimiento, hacer simulaciones de flujo de fluidos (streamline), definir los puntos piloto, aplicar los AGs (optimización), hacer simulaciones Geoestadísticas (SGSIM) para cada propiedad y actualizar la población de individuos. La Figura 1 presenta un diagrama que resume toda la secuencia que hace el programa durante su ejecución (Romero, 2000; Romero et al., 2000).
Simulación Streamline
Para definir la "estratificación social" de cada individuo y, por ende, los operadores genéticos a aplicar, es necesario determinar la Función Objetivo (Ecuación 1) (Baker, 1985) y para esto, es necesario tener una producción de aceite simulada, esta curva se obtiene utilizando un simulador streamline, el cual, es muy conveniente para esta metodología debido a su gran velocidad de convergencia (Batycky, 1997; Batycky et al., 1997; Caers, et al., 2001; Wang et al., 2000).
Los archivos "Grid_Pozos.prn", "Field.prn" y "Production.prn", necesarios para la ejecución del simulador, no cambian durante el proceso de ajuste histórico; por el contrario, los archivos "Files.prn" y "Fluid.prn" deben ser actualizados para cada individuo (realización), ya que las propiedades roca – fluido (permeabilidades relativas), son cromosomas dinámicos y en cada generación van siendo modificados por el AG (Deutsch et al., 1998).
Los datos de las propiedades se encuentran organizados en archivos texto, existe un archivo de este tipo por propiedad y por individuo, en total se tienen 60 archivos para las tres propiedades petrofísicas consideradas y los 20 individuos. Adicionalmente, los puntos finales de las permeabilidades relativas se encuentran en otro archivo plano.
El programa diseñado hace uso de la dependencia que existe entre las permeabilidades y sólo se almacenan los datos de permeabilidad horizontal en X, los datos de permeabilidad en Y y las permeabilidades en Z, son calculados por el simulador, utilizando la información de anisotropías (Ky/Kx y Kz/Kx) suministrada (Dake, 1978 ; Renard et al., 1997).
Definición puntos piloto
La metodología utilizada para disminuir la cantidad de datos a manejar en el AG (upscaling), se denomina Método de los puntos piloto. Los puntos piloto deben considerarse como pseudopozos y se utilizan como los parámetros a variar durante el desarrollo del proceso de optimización con AGs, tal como se describe en la Figura 1. Estos pseudopozos y los pozos son utilizados como datos de entrada al Simulador de Geoestadística, este a su vez se encarga de asignarle valores a todas las celdas que conforman el grid de simulación numérico. Estos puntos serán ubicados por coordenadas (X, Y), de forma análoga a las localizaciones de los pozos verdaderos dentro de un grid de simulación. De acuerdo con el conocimiento heurístico de la geoestadística, se determinó que la cantidad de pseudopozos a utilizar debía ser equivalente al 5% de las celdas que conforman el enmallado (Bissell et al., 1987)
Una vez determinadas las coordenadas (X, Y) para todos los puntos piloto, se deben formar arreglos bidimensionales –uno por cada propiedad petrofísica en consideración– (Figura 2), donde se almacena tanto los pseudopozos como los pozos y su respectiva información petrofísica disponible para las celdas en dirección Z que componen la coordenada (X, Y) seleccionada (Cuypers et al., 1998)
Resumiendo, durante la definición de los puntos piloto el programa se encarga de: calcular la cantidad de celdas que equivalen al 5% del enmallado, seleccionar aleatoriamente las celdas que serán utilizadas, crear arreglos bidimensionales –uno por cada propiedad petrofísica– (Figura 2) e ir a los archivos planos para cargar los datos de cada celda.
Formulación del algoritmo genético modificado
La selección de esta metodología de optimización se hizo teniendo en cuenta las características que hacen de los AGs una técnica conveniente para realizar el ajuste histórico automático en yacimientos de hidrocarburos, una vez este se formula como un problema de optimización (Chen et al., 1974; Davis, 1991; Yang et al., 1987).
La primera característica es que los AGs pueden ser usados eficazmente para la optimización de funciones "ruidosas", porque no requieren información adicional (tales como derivadas) de la función que va a ser maximizada o minimizada (Mitchell, 1996; Stoffa et al., 1991; Thomas et al., 1971).
La segunda característica esta muy ligada a la primera. Porque los AGs usan búsquedas aleatorias, por lo tanto no siguen reglas determinísticas y pueden escapar a mínimos locales. Esta característica les da el potencial para alcanzar óptimos globales (Deschamps et al., 1998; Gomez et al., 1999; Goldberg, 1989).
La capacidad para manejar muchos parámetros es otra característica importante de los AGs. Dependiendo de la complejidad y nivel de detalle necesario, una simulación completa de un yacimiento puede requerir el cálculo de muchos parámetros, generalmente del orden de miles o algunas veces de cientos de miles (Bush et al., 1996; Zalzala et al., 1997).
La cuarta característica de los AGs son sus atributos de paralelismo. Por una parte, los AGs tienen un paralelismo implícito porque ellos trabajan con una población de soluciones y no con una sola solución. De esta manera, varias soluciones propuestas son evaluadas y combinadas durante el proceso de optimización. Adicionalmente, las soluciones propuestas son basadas en la evaluación de soluciones previas, en otros términos, los AGs hacen uso de todas las experiencias exitosas anteriores, gracias a la llamada "memoria implícita". Esto es particularmente importante cuando una función es muy costosa para ser evaluada, como es el caso del ajuste histórico en los yacimientos. De otro lado los AGs tienen el potencial de retornar un conjunto de posibles soluciones, es decir, la población final puede ser usada para evaluar parámetros y predecir la incertidumbre (Ounes, 1992; Sen et al., 1995).
Estructura del genoma y el genotipo
El primer paso en la definición de la estructura de un genoma es la selección de las variables que van a ser incluidas en la optimización. Estrictamente, el genoma debe ser dividido en partes: el genoma dinámico, con las estructuras que cambiarán durante el proceso de optimización y el genoma estático, con la información que contribuirá a la conformación de los modelos numéricos pero permanecerá inalterable a lo largo de la optimización y puede evolucionar después. (Goldberg et al., 1991; Holland, 1975).
Los modelos numéricos de yacimientos requieren especificar un gran número de variables. Para este caso en particular, se han seleccionado las siguientes variables para ser incluidas en la optimización: propiedades petrofísicas (permeabilidad horizontal, porosidad y saturación de agua) tanto en los puntos piloto como en los pozos; parámetros que controlan el proceso geoestadístico (rango en la dirección de máxima correlación, rango en la dirección de mínima correlación y rango de correlación vertical) y permeabilidad relativa en los puntos finales.
La información restante no incluida en el genoma dinámico, tal como: propiedades de los fluidos (PVT), estructura geológica, contacto de fluidos, etc., que es necesaria para una descripción completa del modelo de simulación del yacimiento, esta contenido en el genoma estático y permanece ahí a lo largo de todo el proceso. De aquí en adelante, el término "genoma" hará referencia al genoma dinámico.
El genotipo solo provee la información a partir de la cual el fenotipo es construido. Este tipo de mapeo es conocido como "Embriogenia" porque el genotipo solo establece las reglas para el desarrollo de las características fenotípicas, las cuales son producidas por la interacción de varios genes. En este caso, el genotipo contiene las propiedades petrofísicas de los bloques de los puntos piloto y de pozos, además de parámetros para el control del proceso geoestadístico y permeabilidades relativas en los puntos finales. Cada modelo se construye bajo la interacción de estos parámetros. Un solo genotipo puede producir una variedad de fenotipos, dependiendo de los elementos aleatorios de los métodos geoestadísticos (Bäck, 1996).
En este trabajo, un genoma con estructura no estándar fue seleccionado por las razones ya descritas anteriormente. Las variables han sido divididas en ocho grupos, y a cada grupo de variables tridimensionales, se le asignó un cromosoma separado (porosidad, permeabilidad y saturación de agua). Cromosomas individuales, para cada una de las variables que componen los grupos de parámetros restantes, fueron construidos: parámetros geoestadísticos y permeabilidades relativas para los puntos finales (Figura 3).
Cromosomas de propiedades petrofísicas
Los tres cromosomas de propiedades petrofísicas tienen la estructura que se presenta en la Figura 4. Estos arreglos tridimensionales presentan inserciones para los pozos. Con esta estructura, los elementos vecinos en los arreglos tienen la misma relación espacial a los puntos piloto equivalentes en el fenotipo (Palazzari et al., 1999).
Los valores de las propiedades petrofísicas son representados por números reales (Surry et al., 1997), en lugar de formas binarias. Esto se hace para reducir la complejidad del manejo de los datos (Wright, 1991).
Cromosomas misceláneos
Las variables misceláneas están contenidas en cinco cromosomas unidimensionales. Cada variable es codificada dentro de una cadena de bits binarios con una longitud determinada (Calvete et al., 2001; Martínez, 1990).
Para este trabajo, el número de bits osciló entre cuatro y siete por parámetro, de esta manera las variables fueron discretizadas entre 16 y 128 intervalos, dependiendo de la precisión que se les quisiera dar. Las cadenas binarias son estándar durante todo el desarrollo de la metodología (Whitley, 1999).
El cromosoma para los datos geoestadísticos contiene tres parámetros: rango en la dirección de máxima correlación, rango en la dirección de mínima correlación y rango de correlación vertical. Para este trabajo, un conjunto de sencillo de parámetros controla las simulaciones geoestadísticas en todas las capas (Jensen et al., 1997).
El cromosoma que incluye los parámetros de las permeabilidades relativas en los puntos finales, fue codificado usando números binarios. Este cromosoma se incluyó en el estudio para dar integridad al modelo, aunque su variabilidad se mantuvo al mínimo.
Habiendo definido la estructura del genoma y el procedimiento para codificar las variables dentro de los cromosomas, otro conjunto de estructuras deben ser definidas: las estrategias de selección y los operadores genéticos. La Figura 3 muestra una ilustración simplificada del genoma no–estándar, implementado en este trabajo.
Estrategias de la población
Los AGs trabajan con una población de soluciones potenciales individuales del problema que se está considerando. A medida que el proceso de optimización avanza, la población actual va siendo reemplazada progresivamente por nuevas soluciones. La manera exacta como se logra esto depende de la formulación de las estrategias de la población (Baker, 1985).
Las estrategias de población requieren la definición de tres aspectos principales: la evaluación de la aptitud de cada individuo es decir, obtener una medida de que tan conveniente es un modelo particular (realización) como solución del problema que se está considerando; el procedimiento usado para asignarle descendencia a cada individuo, según la última aptitud calculada; y cómo los individuos entran o salen de la población (actualización) (De Jong, 1975).
Función objetivo
La metodología busca ajustar las propiedades petrofísicas del yacimiento para que este, al ser simulado, reproduzca la curva de producción real del campo, obteniendo de esta forma un modelo que ha sido ajustado automáticamente (sin intervención del ingeniero de yacimientos) y que reproduce lo más parecido posible el comportamiento del campo. De esta forma, este modelo corregido podrá ser utilizado en la predicción de la producción.
El ajuste del modelo se hace optimizando una función objetivo, la cual fue definida como:
El AG busca disminuir hasta su mínima expresión el valor de FO, haciendo ajustes a las variables representadas por los cromosomas, para este caso en particular son: porosidad, permeabilidad, saturación de agua, permeabilidades relativas y parámetros geoestadísticos.
Los cromosomas de porosidad, permeabilidad y saturación de agua, se les aplica una metodología denominada puntos piloto mediante la cual se hace un muestreo de valores aleatorio y estos son los datos que se van a ajustar. Posteriormente, las propiedades petrofísicas son nuevamente distribuidas en todo el modelo mediante una simulación geoestadística, el modelo resultante nuevamente es simulado y se repite el proceso.
Cálculo de la aptitud
En los AGs, la aptitud de un individuo es un indicativo de qué tan bueno es, en particular, para resolver el problema, en comparación con los otros individuos de la población. Para aplicar los AGs en un proceso de ajuste histórico en un yacimiento de hidrocarburos con datos de producción, valores de aptitud deben ser asignados a cada realización (modelo). Estos valores deben reflejar el grado, en que una realización particular puede reproducir la historia de producción. Esto se hace comparando los datos de producción reales con los datos obtenidos por medio de una simulación numérica.
Los datos generados por la simulación geoestadística (H3D) son convertidos (arreglados), por una subrutina del programa, al formato de streamline, generando los diferentes archivos de entrada que contienen los datos de porosidad, permeabilidad y saturación de agua de cada celda del grid utilizado por el programa de simulación. Este paso es de conversión de archivos y se requiere porque los sistemas de coordenadas de los programas de simulación geoestadística y de flujo son diferentes.
El paso final del proceso es el cálculo de la aptitud, el cual se realiza después de que los resultados de la producción simulada están disponibles. Este proceso se realiza internamente en el programa y utiliza como base la Función Objetivo definida por la Ecuación 1. Una vez, se han obtenido los valores de la función objetivo para los 20 individuos, se comparan entre sí y se selecciona el valor más bajo, luego mediante la Ecuación 2 se calcula la aptitud para cada individuo.
Donde:
Aptitud (ni, ng): es el valor de la aptitud de un individuo ni en la generación ng
FO (ni, ng): es el valor de la Función Objetivo de un individuo ni en la generación ng
FOmin (ng): es el valor de la Función Objetivo mínimo en la generación ng
Estrategias de selección
La estrategia de la selección es uno de los factores principales que controlan el desempeño de la optimización. La selección apunta a dar las preferencias a aquellas realizaciones con aptitudes cercanas a la unidad (1), para pasar sus atributos a otras realizaciones.
Una estrategia que proporcione una óptima presión de selección, es crítica para el buen desempeño del AG propuesto. La selección debe favorecer la realización con mejor aptitud, sin causar una convergencia prematura. Una presión de selección óptima debe mantener el equilibrio entre la exploración y la explotación. La fase de exploración requiere que la presión de selección sea baja para que puedan encontrarse nuevos individuos con buenas aptitudes, mientras que la fase de explotación requiere que la presión de selección sea alta para que los individuos con buenas aptitudes se acentúen en espera que ellos produzcan descendencia con aptitudes mejores. Debido a la complejidad del espacio de búsqueda a la exploración se le da la prioridad aunque no debe descuidarse la explotación.
La estrategia de selección implementada en el desarrollo de este proyecto, después de evaluar todas las estrategias propuestas, fue el elitismo combinado con el clasismo; esta estrategia mixta que consiste en clasificar los individuos de acuerdo a su aptitud, creando, por decirlo así, una realeza, una clase media y una clase baja. De acuerdo a su clasificación se aplican los diferentes operadores genéticos (Mitchell et al., 1992).
Esta clasificación se hace mediante el cálculo de una variable que indica la diferencia (amplitud) máxima que existe entre los valores de aptitud calculados para una misma generación, para tal fin se utiliza la Ecuación 3:
Donde:
Dif Aptitud (ng): es valor de máxima diferencia (amplitud) en la generación ng
Aptitudmax (ng): es el valor máximo de la Aptitud en la generación ng
Al valor máximo obtenido se le aplican los porcentajes de elitismo, los cuales son definidos por el usuario dependiendo del comportamiento del proceso; en el desarrollo de este trabajo se utilizaron los siguientes valores:
Reproducción : 10%
Cruzamiento : 70%
Mutación : 20%
Los valores de evaluación del clasismo de los individuos se calculan de utilizando la Ecuación 4:
Donde:
Clasismo (ng): Determina el límite para una determinada clase social en una generación ng
Porcentaje Elitismo: Valor máximo permisible para una clase social
Al valor obtenido para cada una de las clases sociales se le debe sumar uno (1) y de esta forma se determinan los límites superiores. Esto significa que los individuos con aptitudes que se encuentren entre 1 y el 10% de desviación se seleccionarán para reproducción; los individuos con aptitudes que se encuentren entre el 10% y el 80% de desviación, se seleccionarán para cruzamiento; y los individuos con aptitudes superiores al 80% de desviación serán mutados.
De esta forma, todos los individuos que componen una generación se estratifican y, simultánea–
mente, quedan definidos los operadores genéticos que se les aplicarán dependiendo de la clase social a la cual pertenezcan.
Operadores genéticos
Se han creado operadores de cruzamiento no estándar para trabajar con los cromosomas tridimensionales de las propiedades petrofísicas. Existen pocas pautas acerca de cómo estos operadores deberían recombinar sus genes, sin embargo se optó por un sistema sencillo que más adelante se explicará.
Los cromosomas normales fueron combinados aplicando las normas de los operadores genéticos binarios.
Reproducción
En este trabajo se definió la reproducción como la acción de "clonar" un individuo de la generación actual, en la siguiente, logrando de esta forma preservar una memoria implícita respecto a la mejor solución lograda y, de paso, disminuir el tiempo de cómputo requerido, ya que a este individuo no se le debe hacer ni simulación geoestadística ni numérica.
Solo el individuo con aptitud igual a uno (1) será reproducido en cada generación, es decir, solo un individuo tendrá esta condición y será denominado como "rey" dentro de la estratificación clasista diseñada para aplicar el AG.
Sin embargo, en una misma generación uno o más individuos pueden ser clasificados para ser reproducidos, estos individuos cuya aptitud es buena pero no mejor que la del individuo "rey" serán denominados realeza y estos se cruzarán solo con el individuo rey buscando mejorar la aptitud de los individuos descendientes. Este cruzamiento se hace siguiendo las mismas reglas descritas en el párrafo Cruzamiento (Mitchell et al., 1992).
Cruzamiento
Dentro del grupo de individuos seleccionados para cruzamiento se verifica inicialmente que sea un grupo par, es decir, que todos los individuos tengan un compañero de cruce. En caso, de no ser así, el individuo con mejor aptitud dentro de los clasificados para mutación se convierte a individuo de combinación o cruzamiento, completando de esta forma el número par requerido.
El programa se encarga, aleatoriamente, de formar parejas con los individuos disponibles para cruzamiento, los individuos tendrán una y sólo una pareja, y su descendencia serán otros dos individuos, donde se combinan las características genéticas de los dos individuos padres.
En los cromosomas tridimensionales (propiedades petrofísicos), una vez escogidas las parejas y habiendo seleccionado los puntos piloto previamente, se forman dos arreglos bidimensionales; posteriormente, se selecciona aleatoriamente un punto de corte (capa), punto por donde se combinarán los dos padres, tal como se muestra en la Figura 5, de esta forma la descendencia estará compuesta nuevamente por individuos que tienen información genética de ambos padres.
En los cromosomas binarios, el cruzamiento se hará de la forma tradicional en los AGs, haciendo referencia explícitamente al método del punto sencillo; método finalmente seleccionado para aplicar en este trabajo.
Mutación
En este trabajo solo una clase de mutación fue seleccionada y es aplicada sobre el individuo padre y su resultado es un individuo en el cual se modifica uno de sus genes; el tipo de mutación utilizado se denomina de salto.
En los cromosomas binarios el procedimiento es muy sencillo y consiste en cambiar, aleatoriamente un bit de la cadena que compone el cromosoma (0 por 1 o 1 por 0).
En los cromosomas tridimensionales se aplica un procedimiento similar, pero se tiene el cuidado de no cambiar (alterar) las celdas que representan las arcillas, la Figura 6 muestra lo que ocurre en un individuo seleccionado para mutación, en una generación dada.
Las celdas correspondientes a facies de arcillas pueden ser fácilmente reconocidas, ya que los valores de porosidad y permeabilidad fueron ajustados a 0.0001, y en el caso de la saturación de agua, su valor siempre se encuentra por encima del 90%. Cuando se esta ejecutando la subrutina de mutación y el programa encuentra una de estas celdas, inmediatamente salta ese punto piloto y continua con el siguiente.
En las celdas que se pueden mutar, se selecciona un número aleatorio, que se encuentra entre el mínimo y máximo definido para la propiedad petrofísica en evaluación (porosidad, permeabilidad y saturación de agua).
Actualización de la población
Dentro de un AG, una población de soluciones se actualiza constantemente, por norma, las nuevas soluciones reemplazan aquellas cuya aptitud tenga que ser evaluada. Una estrategia de actualización ideal debe poder mantener la diversidad en la población, mientras se va acercando a un óptimo global. El número de generaciones debe ser suficientemente grande para permitir que la población evolucione hasta acercarse al nivel de aptitud requerido. En este trabajo, sin embargo, el número de evaluaciones de la función objetivo se ha restringido a menos de 600 debido a la limitación de recursos computacionales.
Un enfoque generacional fue usado, es decir, la población se reemplazaba casi en su totalidad en cada nueva generación, con excepción del individuo con mejor aptitud, el cual se "clonaba" en la siguiente generación. Los parámetros de AG típicos en este trabajo son: el tamaño de la población es de 20 individuos y el número máximo de generaciones fue de 20; aunque se hicieron pruebas con 25 y 30 generaciones sin encontrar mejorías significativas, mientras que el consumo de tiempo máquina si aumento considerablemente. Al preservar el mejor individuo de una generación a la otra, se hizo una reducción del 5% en el tiempo de cómputo, ya que no fue necesario hacer 400 evaluaciones (en el caso de 20 individuos y 20 generaciones) sino solamente 380.
Simulación gaussiana secuencial
Una vez generados los archivos de entrada al Simulador Geoestadístico (SGSIM) (Deutsch et al., 1998), es necesario leer el archivo texto que contiene los parámetros geoestadísticos considerados y generar un número aleatorio impar de cinco cifras.
Estos datos se utilizan para generar el archivo llamado "SGSIM.prn", el cual contiene la siguiente información: nombres y rutas para los archivos de entrada de datos y salida de resultados, valores mínimo y máximo permitidos, número de celdas en todas las direcciones (X, Y y Z) que componen el modelo, "semilla" a utilizar en la simulación, rango en la máxima dirección de correlación, rango en la mínima dirección de correlación, rango vertical de correlación, ángulos de anisotropía, tipo de estructura del variograma, tipo de Kriging, nugget y sill.
Tal como se puede evidenciar, los nombres de los archivos de entrada y salida, y la información proveniente del cromosoma de parámetros geoestadísticos, son los únicos datos que se actualizan constantemente, los demás se mantienen constantes.
De acuerdo con el análisis de anisotropía hecho, el ángulo de la elipse de búsqueda es de 92° (358° en azimut); el tipo de estructura del variograma seleccionado fue el modelo exponencial; el tipo de Kriging utilizado fue Ordinary Kriging (OK); el nugget se definió como cero (0) y el sill es uno (1) por defecto, ya que el programa normaliza las variables de entrada (Jensen et al., 1997).
Una vez se han generado los archivos texto de geoestadística, estos deben ser convertidos a formato streamline para que puedan ser utilizados por el simulador en la siguiente generación. Adicionalmente, se debe tener presente que algunas celdas del modelo total se encuentran inactivas y por lo tanto estas deben ser nuevamente deshabilitadas. Los archivos acá generados reemplazan a los existentes, lo que facilita que el proceso pueda ser completamente cíclico (WU et al., 1998).
CASO DE CAMPO: AREA 07, ZONA C, CAMPO LA CIRA (COLOMBIA)
El campo La Cira–Infantas esta localizado en la cuenca del Valle Medio del Magdalena (VMM) en Colombia (Figura 7). Se encuentra ubicado en la parte central de la antigua Concesión De Mares, al Este del río Magdalena y al Sur del río Sogamoso, abarcando un área de aproximadamente 160 km2; a una distancia aproximada de 22 km al SE de la Ciudad de Barrancabermeja y a aproximadamente 250 km al NNE de Bogotá (Figura 7). El VMM esta limitado al Este por la Cordillera Oriental, al Oeste por la Cordillera Central, y se extiende desde las localidades del Banco (Magdalena) en el Norte hasta Honda (Tolima) en el Sur (Dengo et al., 1993).
Campo La Cira: Esta estructura consiste de un anticlinal en forma de domo alargado en dirección N–S al Noroeste del Anticlinal de Infantas, con cabeceo (plunge) hacia el Norte y hacia el Sur y está cortada, al Este del eje del Anticlinal, por la falla La Cira, que es una falla inversa de alto ángulo (70°–80°) que buza hacia el Occidente y cuyo desplazamiento oscila entre 200 y 300 pies en el tope de la estructura. Hacia el Este de la falla La Cira la estructura se hunde un poco en forma de "U" a manera de sinclinal entre esta falla y la falla de Infantas. De acuerdo con los datos de producción del campo se puede considerar que la falla La Cira actúa como una barrera efectiva entre el flanco Occidental y Oriental de la estructura. Existe en este campo un gran número de fallas transversales al eje de la estructura las cuales son normales con buzamientos entre 80° y 90° y desplazamientos de hasta 250 pies y que dividen al campo en varios bloques. Esta estructura tiene una longitud aproximada de nueve km y un ancho de seis km. Los buzamientos de la estructura hacia el Norte y el Oeste son de aproximadamente 10° a 15°.
El Campo La Cira produce de tres zonas "A", "B" y "C" (Figura 8). La zona "C" es un yacimiento de arenas fluviales de permeabilidad baja a moderada. Esta zona contiene aproximadamente el 80% del OOIP en el Campo La Cira. Las zonas "C" y "B" producen de la Formación Mugrosa de edad Eoceno – Oligoceno y la zona "A" produce de la formación Colorado de edad Oligoceno.
En la actualidad se han perforado en el área de la Cira–Infantas 1716 pozos, de los cuales hay aproximadamente 580 pozos productores activos, 81 pozos inyectores de agua activos, 592 pozos productores inactivos, 106 pozos inyectores inactivos y 357 pozos abandonados. El OOIP del campo la Cira–Infantas es de 3594 Mbls de 24° API. La producción promedio de aceite actual es de 5700 BOPD (Diciembre de 2002), con una producción de aceite acumulada de 798,15 Mbls y una inyección acumulada de 957,4 Mbls (Diciembre de 2001).
En el área 07, la zona C inició su explotación en 1933 con el pozo LC–745 con 1132 bopd. El principal desarrollo de esta área se llevó a cabo entre los años 1933 y 1941 cuando se perforaron 124 pozos, de los cuales 99 penetraron la zona C. La inyección se inició en 1971 con modelos regulares de seis y siete puntos, modificados posteriormente a modelos de cuatro a siete puntos, por problemas mecánicos de los pozos.
Para realizar el modelo estratigráfico y el modelo petrofísico se seleccionaron 65 pozos, los cuales se pueden observar en la Figura 9. Algunos de los criterios que se tuvieron a la hora de realizar esta selección fueron:
- Pozos Corazonados (Carrillo et al., 1990).
- Pozos perforados más recientes (calidad registros eléctricos).
- Que tuvieran una buena distribución areal (cobertura total del área).
- Que estuviera representada la geomorfología de las unidades definidas.
Modelo sedimentario
Para la definición del modelo sedimentario y diagenético se contó con la información litológica (corazones) del pozo La Cira 1884, perforado y corazonado en 1988 como reemplazo del pozo LC–1133. En la descripción de los 350 pies de corazón del pozo LC–1884, que incluye la mayoría de las arenas y arcillas que conforman la unidad "C", se pudieron identificar facies correspondientes a: depósitos de canales fluviales y depósitos de llanura de inundación (Reyes et al., 1989).
Para la identificación de estas facies, se utilizó como guía los modelos y conceptos resultantes del estudio realizado por la División de Yacimientos, Geología de Desarrollo y Asociados y el Distrito de Producción El Centro de Ecopetrol en 1992.
Arenas de barras de meandro
Estas facies arenosas son las más características dentro de la secuencia estudiada en muestras de corazón, con espesores que oscilan entre 10 y 35 pies caracterizados por presentar hacia la base de las arenas de grano grueso a conglomerático, intraclastos arcillosos y fragmentos leñosos, descansando sobre superficies de erosión, con estratificación cruzada de alto ángulo en artesa que gradualmente cambia a estratificación plano paralela a subparalela discontinua y a ondulitas, acompañado por disminución gradual del tamaño de grano hasta llegar a grano fino pasando finalmente a facies arcillosas de planicie de inundación, (Bernal et al., 1992). Normalmente esta secuencia se ve interrumpida debido al desarrollo de apilamientos verticales ("stacking point bars"), estableciendo comunicación vertical entre las diferentes unidades de la zona "C" (Bernal et al., 1992).
Rellenos de canales abandonados
Estas facies limo–arcillosas se caracterizan por presentar la base del canal, normalmente de poco espesor, suprayacida por una secuencia de material limoso o arcilloso que representa el gradual o súbito abandono del canal (Bernal et al., 1992).
Lodolitas de llanura de inundación
Conformada por arcillolitas varicoloreadas (gris verdosa, rojiza, amarillenta, etc.) y por limolitas gris rojizas con restos de raíces, indicios de exposición subaérea y sectores bioturbados rellenos de arenas calcáreas (Bernal et al., 1992).
Arenas finas y limos de borde de canal (Natural Levee)
Constituyen los umbrales de los canales y consisten de material clástico fino con espesores que varían entre 2 y 10 pies aproximadamente (Bernal et al., 1992).
Arenas finas y limos de desborde de canal (Crevasse Splay)
Consiste de arenas finas, normalmente con tendencia granocreciente al tope, espesores de 4 a 10 pies aproximadamente (Bernal et al., 1992).
Modelo Estratigráfico
Los cambios en las propiedades petrofísicas con respecto a la posición estratigráfica son proporcionales al grado de preservación de facies idénticas depositadas bajo condiciones variables de A/S (acomodación y suministro de sedimentos). En areniscas con estratificación cruzada, los cambios en porosidad y permeabilidad son exactamente coincidentes con variaciones sutiles en los atributos que son función de la posición estratigráfica (Ramón et al., 1997).
Teniendo en cuenta las anteriores consideraciones, se procedió a clasificar cada una de las arenas presentes en la zona "C" (objeto de este estudio) de acuerdo con su posición estratigráfica, clasificando estas de acuerdo a su unidad genética (depósitos de Canales o depósitos de Llanuras de Inundación). Las "barras de arenas" y los apilamientos de "barras de arenas" se clasificaron bajo la denominación de Point Bars (PB); las arenas Crevasse Splay y Natural Levee se clasificaron bajo sus respectivos nombres y se encontrarán en adelante con la siguiente nomenclatura: CS y NL respectivamente. Adicionalmente, las arcillas que actúan como sellos tanto en los depósitos de canal (clay plugs) como en los depósitos de llanuras de inundación fueron clasificadas, quedando denominadas como CP y FP respectivamente.
Esta clasificación permitió que se generaran variables discretas, así: 1 para Point Bars (PB), 2 para Crevasse Splay (CS), 3 para Natural Levee (NL) y 4 para Clay Plugs (CP) y arcillas de Flood Plain (FP); las cuales fueron utilizadas para generar el modelo petrofísico que se utilizó para determinar la porosidad y permeabilidad en todos los pozos involucrados, es importante resaltar que las arcillas se unieron bajo una misma clasificación por: simplificación de los datos manejados y por que las arcillas, en este caso particular, no tienen importancia económica.
En el desarrollo de este trabajo se conservó la nomenclatura que se utilizó en el estudio "Modelos de Caracterización del Yacimiento: Geológico, de Distribución de Fluidos y Petrofísicos" de Bernal et al. (1992), para zonificar la zona "C" superior (C1 y C2); la subzona C3 no fue tenida en cuenta por su carácter acuífero.
El espesor promedio para el intervalo seleccionado es de 347 ft aproximadamente, en donde se identificaron 16 arenas de barras de arena, "natural levee" y "crevasse splay", las cuales fueron asociadas a 16 unidades genéticas, cada una de ellas representando ciclos de sedimentación coetáneos (Figura 10). Se destaca la relativa mayor continuidad de las fajas de meandros en dirección Norte – Sur, dirección en la cual se creen corrían las corrientes principales.
En términos generales se pueden dividir las dos subzonas presentes de la siguiente manera:
En la subzona C1 se identificaron 6 unidades genéticas llamadas de base a tope: C1A1, C1A, C1B1, C1B2, C1C y C1D. En la secuencia que separa las subzonas C1 y C2 se presenta una unidad no continua denominada C1C2 que registra condiciones de alta energía (tipo canal) dentro de una "llanura de inundación" (FP), la cual se comunica verticalmente con la unidad C2A de la subzona C2 (Bernal et al., 1992).
En C2 se han identificado 9 unidades que presentan un mayor acoplamiento vertical que el observado durante la depositación de las unidades del C1. Estas unidades se denominan de base a tope: C2I, C2H, C2G, C2F, C2E, C2D, C2C, C2B y C2A (Bernal et al., 1992).
Modelo estructural
La profundidad de tope y base de cada una de las unidades genéticas fue definida utilizando los registros eléctricos y en particular el registro litológico disponible para cada pozo (SP o GR). Adicional a las unidades descritas en el párrafo anterior, se relacionaron dos marcadores adicionales denominados TOPE, BASE y C3CB, las profundidades de estos, fueron determinadas utilizando la sísmica 3D y se tomaron del estudio "Evaluación Integrada Yacimientos del Campo La Cira–Infantas" (Lobo et al., 1999).
Los marcadores TOPE, C1D y C3CB fueron cartografiados y se utilizaron para definir la geomorfología del área en estudio. El marcador BASE fue utilizado solo para definir la base de la unidad genética C2I y no fue posible cartografiarlo debido a la escasez de datos, ya que fueron pocos los pozos que llegaron a esta profundidad.
Para definir la geomorfología en la parte superior de la zona "C" se seleccionó la unidad genética C1D (Figura 11(a)), este patrón estructural fue utilizado en la simulación geoestadística. Para la parte inferior existían dos posibles marcadores a utilizar: BASE y C3CB, siendo C3CB el más profundo; sin embargo, el mapa hecho con los puntos de control de BASE no era muy representativo de la geomorfología existente, por tal motivo se seleccionó el marcador C3CB (Figura 11(b)) para definir la geomorfología de la parte inferior de la zona "C" del área seleccionada.
SELECCIÓN DEL GRID SIMULACION
Con los modelos sedimentológico, estratigráfico y estructural definidos, se procedió a definir el modelo litológico más probable del área. Para tal fin, se generaron 51 realizaciones litológicas, las cuales fueron posteriormente evaluadas bajo el criterio de conectividad de los geo–objetos presentes en el yacimiento (Deutsch et al., 1998; Idrobo, 1999).
Una de las aplicaciones de evaluar la conectividad de los geo–objetos es el ranqueo de múltiples realizaciones geoestadísticas. Los volúmenes de celdas conectadas pueden ser usados para clasificar múltiples realizaciones geoestadísticas, por ejemplo de alta, media y baja conectividad. El ranqueo solo puede ser desarrollado a partir de un número escalar, pero generalmente el carácter del modelo tridimensional no esta referenciado por escalares. Sin embargo, las medidas promedio de conectividad consideradas aquí, suministran una forma de ranquear realizaciones. Para este propósito se dispone del programa RANK_OBJ, desarrollado por Deutsch (1998).
Una vez seleccionado el modelo litológico más representativo para el área utilizada en la definición del modelo estratigráfico, se hicieron 20 descripciones petrofísicas de dicho modelo. Posteriormente y por razones prácticas, se hizo una reducción del modelo a caracterizar, para seleccionar esta área se escogieron tres patrones de inyección/producción, los cuales delimitaron un nuevo grid.
Modelo de simulación
El área seleccionada para llevar a cabo el ajuste histórico automático, corresponde a tres modelos (patrones) de inyección/producción, su ubicación dentro del área de modelamiento estratigráfico se puede observar en la Figura 12 (Bradley, 1987). Estos tres patrones fueron seleccionados debido: a su buena respuesta al proceso de recobro secundario por inyección de agua, y a la no presencia de fallas, lo que simplificaba el modelo numérico (Buckley et al., 1942; Dykstra et al., 1950).
El área seleccionada tiene una superficie de aproximadamente 376 acres y esta compuesta por 12 pozos: LC–1131, LC–1137, LC–1181, LC–1208, LC–1209, LC–1210, LC–1212, LC–1213, LC–1214, LC–1229 LC–1247 y LC–1819, todos (excepto el pozo LC–1819) tuvieron producción primaria.
Las coordenadas de esta área son:
Xo = 1'035,040 m : Yo = 1'260,994 m
Xf = 1'036,085 m : Yf = 1'262,450 m
Una vez definido este nuevo grid, se optó por deshabilitar algunas de las celdas que componen este enmallado; estas, no se tuvieron en cuenta porque hacen parte del área de influencia de otros pozos que no fueron considerados dentro de este estudio. En la Figura 13 se pueden observar marcadas con X y sombreadas, las celdas que finalmente quedaron activas dentro del desarrollo del presente trabajo (Satter et al., 1994).
Para resumir los ajustes que se le han hecho al enmallado, se presentan los siguientes datos: grid de referencia, 60 x 60 x 1000; grid de geoestadística, 60 x 60 x 347; y grid de simulación escalado teniendo en cuenta tanto celdas activas como inactivas, 19 x 28 x 25 (total 13300 celdas), el tamaño de cada bloque es de 55 m x 52 m y con tamaño variable en z.
RESULTADOS
Una vez finaliza la ejecución del programa, este automáticamente genera un libro de Microsoft Excel compuesto por cinco hojas de cálculo donde se relacionan los resultados obtenidos después de haber hecho el ajuste histórico automático.
En la hoja llamada "Presentacion_1" se encuentran graficados los datos de producción de aceite (bopd) reales, simulados y promedio utilizado en streamline (Figura 14).
En la hoja llamada "Presentacion_2", se presenta una tabla con los valores de permeabilidades relativas finalmente utilizados durante el proceso de simulación streamline, en la parte inferior de esta se encuentran los puntos finales de las permeabilidades relativas, así como también los valores de saturación de agua connata, la saturación de aceite residual y los factores de Corey (Corey, 1954). La Tabla 1 se presenta a continuación y allí se resumen estos parámetros. En la Figura 15 presenta de manera gráfica los valores relacionados en la Tabla 1.
En la hoja llamada "Hoja1" se relaciona la siguiente información: tiempo de máquina, evolución de los individuos durante las 20 generaciones, individuo rey en cada generación, los porcentajes de selección definidos por el usuario y finalmente los puntos piloto seleccionados por el programa. En la Tabla 2, se observan todos los datos anteriores a excepción de los puntos piloto, estos no se incluyeron debido a la magnitud de datos generados y a que estos no son un factor concluyente del método y se usan para revisar el comportamiento del programa.
En la hoja llamada "Cromosomas" se presentan las tablas de equivalencias generadas para los cromosomas binarios, estas tablas son utilizadas por el programa para codificar y descodificar los valores de las variables que los utilizan (puntos finales de las permeabilidades relativas y los parámetros geoestadísticos).
Para validar el modelo obtenido se calcularon los percentiles 10, 20, 30, , 80, 90 y 100 para todos los datos que componen cada propiedad petrofísica (porosidad, permeabilidad y saturación de agua) y se compararon con los percentiles 10, 20, 30, , 80, 90 y 100 del individuo 2 de la población inicial, este individuo fue seleccionado aleatoriamente entre los 20 individuos (realizaciones) generadas como población inicial. Los resultados obtenidos se pueden observar en la Tabla 3.
Adicional al cálculo de los percentiles, se hicieron gráficas donde se puede evidenciar el comportamiento de la propiedad, en el individuo inicial y en el individuo final. En este trabajo se muestra el comportamiento de la permeabilidad en seis capas del modelo de simulación (1, 5, 10, 15, 20 y 25). La Figura 16, muestra las capas que se relacionaron anteriormente, teniendo en cuenta que la capa 1 es la base (más profunda) y la capa 25 es el tope (superior) de la zona "C" después de ser escalada.
Se evidencia que las propiedades petrofísicas han sido modificadas dentro de ciertos rangos permitidos, logrando de esta forma mejorar el ajuste histórico (Figura 14) y disminuyendo el valor de la función objetivo de 1'663,364 en la primera generación a 640,494 en la vigésima generación (Tabla 2).
CONCLUSIONES
- Se ha logrado aplicar una metodología algorítmica para obtener un modelo de distribución en 3D de las propiedades petrofísicas condicionado a los datos estáticos y dinámicos disponibles para una parte del área 7 del campo La Cira (yacimiento fluvial), con éxito.
- En este trabajo, se muestra que la computación evolutiva puede ser aplicada con éxito como herramienta para la caracterización de yacimientos de hidrocarburos condicionando el modelo geológico y estructural a los datos de producción.
- Tal como se evidencia en la Tabla 2 (Relación evolución individuos), la función objetivo se va reduciendo, al igual que los valores promedio de las funciones objetivo en cada generación. Esta mejoría se puede ver en las Figuras 14 y 16.
- Para aplicar la metodología se elaboró un programa llamado INVERDINAMICA ©, desarrollado en plataforma PC y bajo ambiente Windows; el programa fue compilado, y presentado como un ejecutable.
- Esta metodología ayudará, a los ingenieros de yacimientos, a realizar la calibración (ajuste histórico) del modelo propuesto, disminuyendo las horas hombre requeridas para realizar este proceso.
- La combinación de los AGs (método de optimización global), el método de los puntos piloto, la Simulación Gaussiana Secuencial (modelamiento geoestadístico) y la simulación streamline (simulador numérico) proporcionan una herramienta robusta para ser utilizada en la solución de problemas inversos aplicados a la industria del petróleo. Se genera de esta forma una solución muy económica en términos de costo computacional, eficiente y totalmente automática.
- La técnica definida en este trabajo puede ser aplicada tanto a yacimiento en producción primaria como en yacimientos sometidos a la inyección de agua. Para yacimientos en recobro primario se haría necesario el uso de un simulador convencional, como consecuencia, los tiempos de cómputo aumentarán considerablemente.
- Utilizar un modelo sin escalar, es posible, ya que el simulador de streamline permite su uso y, seguramente, con el mejoramiento de las velocidades de cómputo en los equipos venideros, será posible obviar los errores que se generan al escalar los modelos.
- La metodología mostró ser una técnica apropiada para encontrar descripciones de yacimientos que hacen honor a los datos de producción, información de los pozos y a los rasgos geológicos; además es capaz de manejar gran cantidad de parámetros, lo cual es un problema cuando se trabaja en modelos de simulación de yacimientos.
- La metodología fue aplicada exitosamente en la parte superior de las arenas "C" de 3 patrones inyección/producción (12 pozos) del área 7 del Campo La Cira, este es un yacimiento heterogéneo de ambiente de depositación fluvial.
- El análisis de la conectividad de las arenas es un método efectivo para clasificar las realizaciones litológicas y de esta forma se puede hacer una selección rápida de modelos ubicados en algún percentil en particular. En esta tesis el percentil utilizado fue el P–50.
- Para este estudio en particular, se encontró que la incertidumbre generada en la determinación de la Saturación de Agua, después de 30 años de producción primaria, es mucho más significativa que la proveniente del cálculo del volumen de arcilla. Por esta razón, se cambió el volumen de arcilla por la saturación de agua.
- El concepto utilizado para diseñar la metodología de los AGs es tan universal que permite ser modificada fácilmente, y se adecua a las condiciones del problema propuesto.
- Al comparar los resultados obtenidos por el simulador con los datos históricos, se observa que aún existen diferencias significativas en la producción al momento de la irrupción del agua, este problema se debe más a condiciones operativas que al método propuesto; se puede observar que el pozo La Cira 1210 es el que mejor ajusta tanto en la tasa de producción como en el corte de agua, esto se explica fácilmente al considerar su ubicación estratigráfica (parte baja de la estructura), lo que implica que la cantidad de gas libre al inicio de la inyección era menor que la de los otros dos pozos; el pozo con menor ajuste es La Cira 1214 donde se observa que el corte de agua del simulador aumenta rápidamente comparado con el corte de agua histórico. Puede decirse que este es el pozo estructuralmente más alto, y por lo tanto, el que tiene mayor efecto por presencia de gas. Esta condición no es compatible con el simulador streamline, ya que este no maneja fluidos compresibles.
RECOMENDACIONES
- No se evaluaron los beneficios de aplicar un método de optimización local en el individuo rey al terminar la ejecución del Algoritmo Genético, por falta de tiempo. Se recomienda evaluar la implementación de un método de optimización local al finalizar la ejecución del AG.
- Aumentar las propiedades petrofísicas en consideración, incluyendo el volumen de arcilla como variable; incorporar parámetros adicionales tales como la presión capilar, propiedades PVT, características del acuífero, Skin, etc.
- La versión actual del software INVERDINAMICA© es la 2003.2, se recomienda continuar trabajando en el mejoramiento de este programa implementando más características que lo hagan más flexible. Durante el desarrollo de este trabajo de investigación se generaron varias aplicaciones programadas en VBA (Visual Basic para Aplicaciones) en Microsoft Excel, las cuales se deben continuar desarrollado y finalmente, deben ser integradas a INVERDINAMICA©, automatizando el proceso completo.
AGRADECIMIENTOS
Los autores quieren expresar su agradecimiento a Ecopetrol S.A. por la financiación de la totalidad de este proyecto y al Instituto Colombiano del Petróleo (ICP) por el apoyo logístico brindado. A los Ingenieros Jorge Mantilla V., Edgar Martínez H. y Edwin Pineda C. por su ayuda incondicional.
[back]AGRADECIMIENTOS
Los autores quieren expresar su agradecimiento a Ecopetrol S.A. por la financiación de la totalidad de este proyecto y al Instituto Colombiano del Petróleo (ICP) por el apoyo logístico brindado. A los Ingenieros Jorge Mantilla V., Edgar Martínez H. y Edwin Pineda C. por su ayuda incondicional.
BIBLIOGRAFÍA
Bäck, T., 1996. "Evolutionary algorithms in theory and practice". Oxford University Press, New York. [ Links ]
Baker, J. E., 1985. "Adaptive selection methods for genetic algorithms". Grefenstette, J. J. ed., Proceedings of the First International Conference on Genetic Algorithms and their Applications, Lawrence Erlbaum Associates, Hillsdale, New Jersey. [ Links ]
Batycky, R. P., 1997. "A three-dimensional two-phase field scale streamline simulator". PhD Thesis, Stanford University, Dept. of Petroleum Engineering, Stanford, CA. [ Links ]
Batycky, R. P., Blunt, M. J., and Thiele, M. R., 1997. "A 3D Field Scale Streamline-Based Reservoir Simulator", SPE Reservoir Engineering, 246-254. [ Links ]
Bernal, M. C., 1992. "Modelos de caracterización del yacimiento: geológico, de distribución de fluidos y petrofísicos". Ecopetrol. [ Links ]
Bissell, R. C., Dubrule, O., Lamy, P., Swaby, P. and Lepine, O., 1987. "Combining geostatistical modelling with gradient information for history matching: the pilot point method". Paper SPE 38730, presented at the 1997 SPE Annual Technical Conference and Exhibition, San Antonio, Texas, 5-8. [ Links ]
Bradley, H., 1987. "Petroleum engineering handbook". Society of Petroleum Engineers, Richardson, Texas. [ Links ]
Buckley, S. E. and Leverett, M. C. 1942. "Mechanisms of fluid displacement in sands". Trans., AIME 146, 107-116. [ Links ]
Bush, M. D. and Carter, J. N., 1996. "Application of a modified genetic algorithm to parameter estimation in the petroleum industry". Dagli et al. eds., Intelligent Engineering Systems through Artificial Neural Networks 6, ASME Press, New York, 397-402. [ Links ]
Caers, J., Krishnan, S., Wang, Y. D., and Kovscek, A. R., 2001. "A geostatistical approach to streamline-based history matching". In proceedings of the Stanford Center for Reservoir Forecasting, Stanford, CA. [ Links ]
Calvete, F., 2001. "Computación evolutiva: algoritmos genéticos y simulated annealing, técnicas meta-heurísticas de optimización en ingeniería de petróleos". IX Congreso Colombiano del Petróleo, Asociación Colombiana de Ingenieros de Petróleos (ACIPET), Bogotá. [ Links ]
Carrillo, L. F., 1990. "Análisis petrofísicos especiales de corazones, pozo La Cira 1884". Ecopetrol - ICP, Piedecuesta. [ Links ]
Chen, W. H., Gavalas, G. R., Seinfeld, J. H., And Wasserman, M. L., 1974. "A new algorithm for automatic history matching". SPEJ, 593-608. [ Links ]
Corey, A. T., 1954. "The interrelation between gas and oil relative permeabilities". Producers Monthly, 38-41. [ Links ]
Cuypers, M., Dubrule, O., Lamy, P. and Bissell, R., 1998. "Optimal choice of inversion parameters for history-matching with the pilot point method". Proceeding of the Sixth European Conference on the Mathematics of Oil Recovery. [ Links ]
Dake, L. P., 1978. "Fundamentals Of Reservoir Engineering". Developments in Petroleum Science 8, Elsevier, Amsterdam. [ Links ]
Davis, L., 1991. "Handbook of genetic algorithms". Van Nostrand Reinhold, New York. [ Links ]
De Jong, K. A., 1975. "An analysis of the behavior of a class of genetic adaptive systems". Ph.D. dissertation, University of Michigan, Ann Arbor. [ Links ]
Dengo, C. A. and Covey, M. C., 1993. "Structure of the Eastern Cordillera of Colombia: Implications for Trap Styles and Regional Tectonics". AAPG Bulletin, 77/8, 1315-1337. [ Links ]
Deschamps, T., Grussaute, T., Mayers, D. and Bissell, R., 1998. "The results of testing six different gradient optimisers on two history matching problems". Proceedings of the Sixth European Conference on the Mathematics of Oil Recovery. [ Links ]
Deutsch, C. V. and Journel, A. G. 1998. "GSLIB: Geostatistical software library and user's guide". second edition, Oxford University Press, New York. [ Links ]
Deutsch, C. V. 1998. "Fortran programs for calculating connectivity of three-dimensional numerical models and for ranking multiple realizations". Computers & Geosciences, 241, 69. [ Links ]
Dykstra, H. and Parsons, H. L. 1950. "The prediction of oil recovery by waterflooding". Secondary Recovery of Oil in the United States, 2nd ed., API, New York, 160-174. [ Links ]
Goldberg, D. E., 1989. "Genetic Algorithms in Search, Optimization, and Machine Learning". Addison-Wesley Publishing Company, Inc., Reading, Massachusetts. [ Links ]
Goldberg, D. E. and Deb, K., 1991. "A comparative analysis of selection schemes used in genetic algorithms". Rawlins, G. J. E. (ed.), Foundations of Genetic Algorithms, Morgan Kaufmann. [ Links ]
Gomez, S., Gosselin, O., and Barker, J. W., 1999. "Gradient-based history-matching with a global optimization method". Paper SPE 56756 presented at the 1999 SPE Annual Technical Conference and Exhibition, Houston, Texas, 3-6. [ Links ]
Holland, J. H., 1975. "Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence". University of Michigan Press, Ann Arbor, Michigan. [ Links ]
Idrobo, E. A. 1999. "Characterization and ranking of reservoir models using geostatistics and streamline simulation". PhD Dissertation, Texas AYM University. [ Links ]
Jensen, J., Lake, L., Corbett, P., and Goggin, D., 1997. "Statistics for petroleum engineers and geoscientists". Prentice Hall Petroleum Engineering Series, New Jersey. [ Links ]
Lobo, A., 1999. "Evaluación integrada de yacimientos, campo La Cira-Infantas". Ecopetrol, Bogotá. [ Links ]
Martínez, J., 1990. "Fundamentos de algoritmos genéticos". II Congreso Colombiano de Neurocomputación, Universidad Nacional de Colombia, Bogotá. [ Links ]
Mitchell, M., Forrest, S., and Holland, J. H., 1992. "The royal road for genetic algorithms: fitness landscapes and ga performance". Varela, F. J. and Bourgine, P., (eds.), Towards a Practice of Autonomous Systems, Proceedings of the First European Conference on Artificial Life, MIT Press. [ Links ]
Mitchell, M., 1996. "An introduction to genetic algorithms". The MIT Press, Cambridge, Massachusetts. [ Links ]
Ouenes, A., 1992. "Application of simulated annealing to reservoir characterization and petrophysics inverse problems". PhD Thesis, New Mexico Institute of Mining and Technology. [ Links ]
Ramon, J.c., 1997. "Characterización and prediction of reservoir architecture and petrophysical properties in fluvial channel sandstones, Middle Magdalena Basin, Colombia". CTYF - Ciencia, Tecnología y Futuro, Piedecuesta, Santander: Ecopetrol, ICP , 1: 3. [ Links ]
Renard, Ph. and De Marsily, G., 1997. "Calculating equivalent permeability: a review". Advances in Water Resources, 20: 253-278. [ Links ]
Romero, C.E., 2000. "A genetic algorithm for reservoir characterisation using production data". PhD Dissertation, University of London, Royal School of Mines. [ Links ]
Romero, C. E., Carter, J. N., Gringarten, A. C. and Zimmerman, R. W., 2000. "A modified genetic algorithm for reservoir characterization". SPE 64765, SPE International Oil and Gas Conference and Exhibition, Society of Petroleum Engineers, Beijing. [ Links ]
Romero, C. E., Carter, J. N., Gringarten, A. C. and Zimmerman, R. W., 2000. "Improved reservoir characterization through evolutionary computation". SPE 62942, SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Dallas. [ Links ]
Reyes, A., Fajardo, A. and Ballesteros, R., 1989. "Descripción macropetrográfica del pozo La Cira 1884";. Ecopetrol-ICP, Piedecuesta. [ Links ]
Satter, A. and Thakur, G. C. , 1994. "Integrated petroleum reservoir management: a team approach". Penn Well Publishing Company, Tulsa, Oklahoma. [ Links ]
Sen, M. K., Datta-gupta, A., Stoffa, P. L., Lake, L. W. and Pope, G. A., 1995. "Stochastic reservoir modeling using simulated annealing and genetic algorithms". SPE Formation Evaluation, 49-55. [ Links ]
Stoffa, P. L. and Sen, M. K., 1991. "Nonlinear multiparameter optimization using genetic algorithms: inversion of plane-wave seismograms". Geophysics, 56, 1794-1810. [ Links ]
Surry, P. D. and Radcliffe, N. J., 1997. "Real representations". Belew, R.K. and Vose, M.D., eds.. Foundations of Genetic Algorithms 4, Morgan Kaufmann Publishers, San Francisco, California. [ Links ]
Thomas, L. K., Hellums, L. J. and Reheis, G. M., 1971. "A nonlinear automatic history matching technique for reservoir simulation models". Paper SPE 3475 presented at the SPE, 46th Annual Fall Meeting, New Orleans, Louisiana, 3-6. [ Links ]
Wang, Y. and Kovscek, A. R.,2000. "Streamline approach for history matching production data". SPE Journal, (4): 353-362. [ Links ]
Whitley, D., 1999. "A free lunch proof for gray versus binary encodings". Proceedings of the Genetic and Evolutionary Computation Conference, Banzhat, W., eds., Morgan Kaufmann, San Francisco. [ Links ]
Wright, A. H., 1991. "Genetic algorithms for real parameter optimisation". Rawlins, G. J. E. ed., Foundations of Genetic Algorithms, Morgan Kaufmann. [ Links ]
Wu, Z., Reynolds, A. C. and Oliver, D. S., 1998. "Conditioning geostatistical models to two-phase production data". SPEJ, 4 (2). [ Links ]
Yang, P-h. and Watson, A. T., 1987. "Automatic history matching with variable-metric methods". Paper SPE 16977 presented at the SPE 62nd Annual Technical Conference and Exhibition, Dallas, Texas, 27-30 . [ Links ]
Zalzala, A. M. and Fleming, P. J., 1997. "Genetic algorithms in engineering systems". The Institution of Electrical Engineers, London, U.K. [ Links ]